|
zum
Abschnitt:
Anwendungen
Bei
allen vorgestellten Anwendungen gehen es um Kombinationen von E−
und B−Feldern.
Wienscher Geschwindigkeitsfilter
In der ersten Anwendung wird ein Gerät zum Filtern
der Geschwindig- keiten
geladener Teilchen vorgestellt. Dies ist vor allem bei radioakti- ven Strahlungsteilchen wichtig, bei denen die Geschwindigkeit ganz unterschiedlich sein kann. Es liegt
hier folgender Aufbau vor:
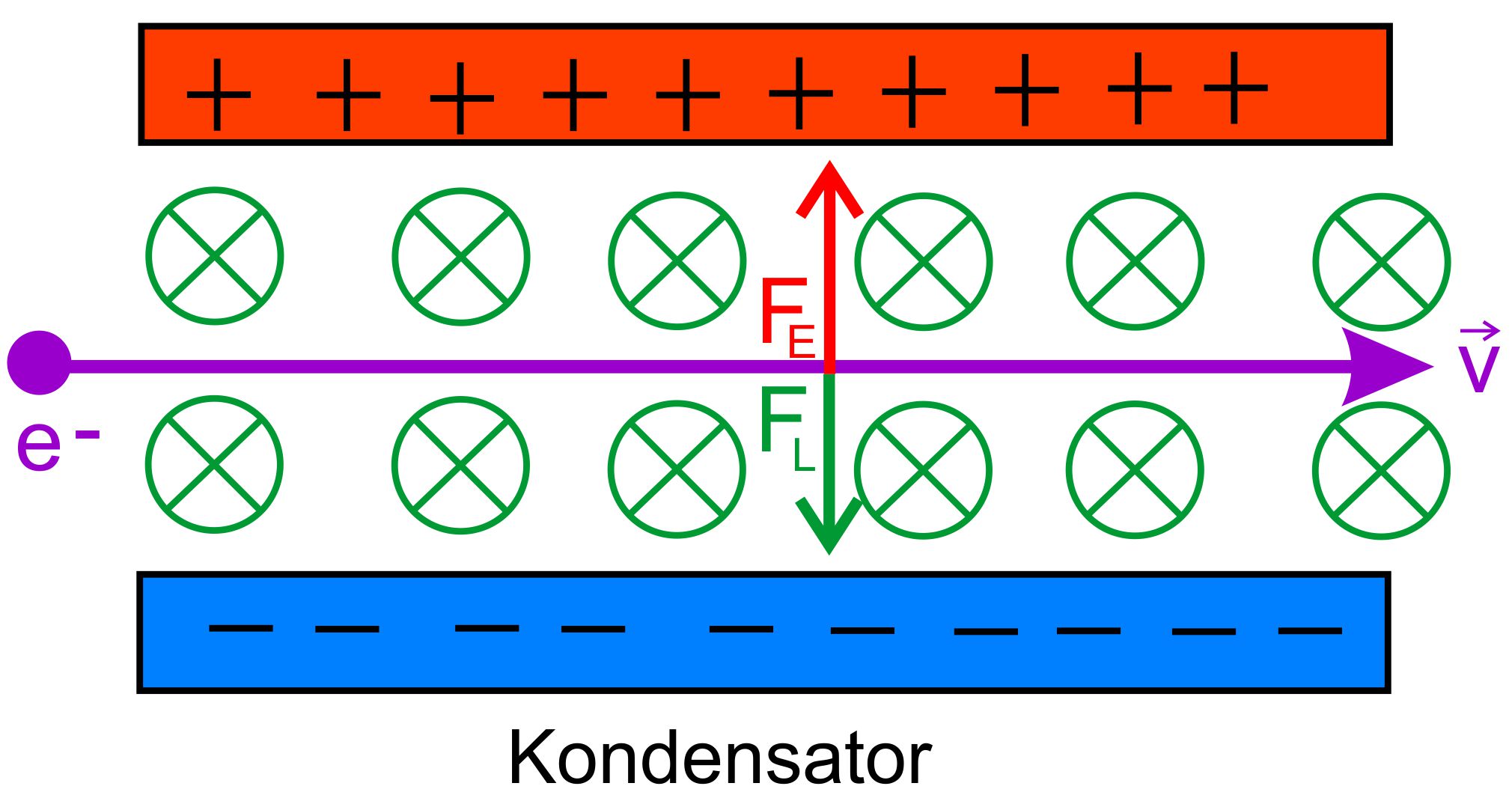
Im Wienschen Geschwindigkeitsfilter werden zwei Felder überein- andergelegt. Einmal ein elektrisches Feld zwischen den Kondensator- platten (E-Feld) und ein magnetisches Feld (B-Feld). Diese Felder stehen senkrecht zueinander. Man sagt auch, dass „gekreuzte“ Felder vorliegen. Es wirken dann die elektrische Feldkraft FE und die Lorentz- kraft FL auf die geladenen Teilchen. Für Elektronen weist die elektri- sche Feldkraft nach oben, die Lorentzkraft nach der Drei-Finger-Regel nach unten. Falls beide Kräfte gleich groß sind, kann sich das Teilchen geradlinig durch die gekreuzten Felder bewegen. Nimmt man positive Ladungen, sind die Kräfte andersherum ausge- richtet.
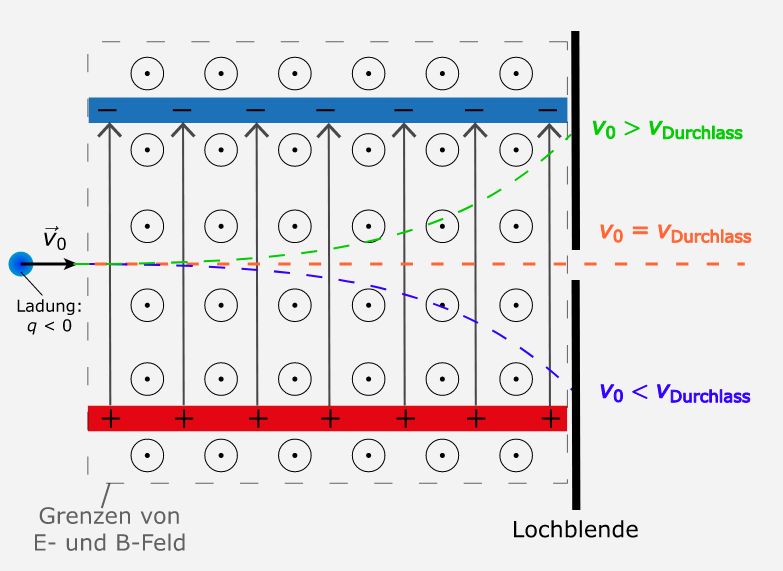
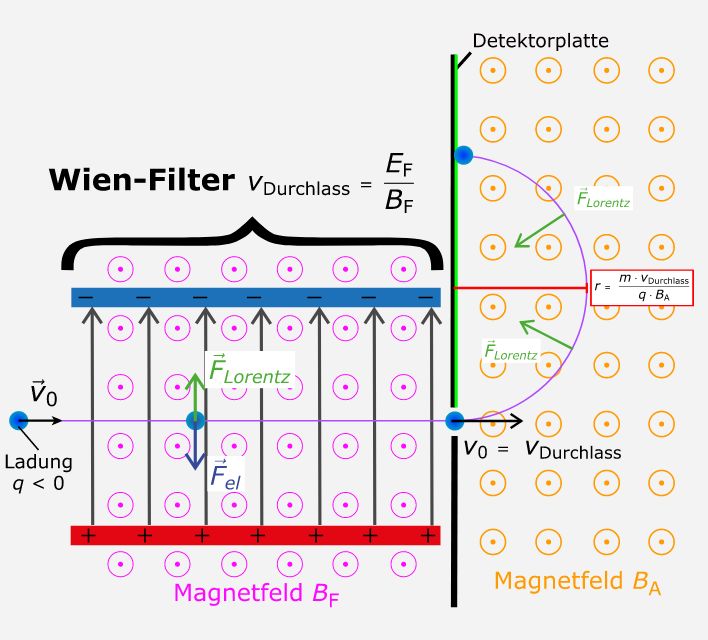
Falls die Geschwindigkeit der Teilchen kleiner als „v“ ist, ergeben sich gekrümmte Bahnen. Wenn also am Ende des Wienfilters eine Blende steht, die nur geradlinige Teilchen durchlässt, können Teilchen mit einer anderen Geschwindigkeit den Filter nicht verlassen. Man weiß also genau, mit welcher Geschwindigkeit die Teilchen aus dem Filter austreten. Da nur FL von v abhängt, gilt also für Teilchen mit größerer Geschwin- digkeit als v, dass FL größer als FE ist, also wird in die Richtung von FL abgebogen, also bei Elektronen nach unten. Für Teilchen mit klein- erer Geschwindigkeit entsprechend andersherum. In der folgenden Abbildung wird dies noch einmal gezeigt:
Quelle:
https://virtuelle-experimente.de/b-feld/anwendung/geschwindigkeitsfilter.php Beachte: die Felder sind anders ausgerichtet als bei
meiner Abbildung! Man kann jetzt durch Änderungen von E und B genau vorgeben, welche Geschwindigkeit die austretenden Teilchen haben sollen. Dies kann bei einigen Anwendungen, z.B. beim Massenspektrometer wichtig sein. Hinweis: der Filter ist übrigens nach Wilhelm Wien benannt. In folgendem Video wird ein solcher Filter mit ganz „normalen“ Geräten einer Schul-Physiksammlung nachgebaut. Quelle: Wienfilter,
Geschwindigkeitsfilter, Wien'scher
Geschwindigkeitsfilter (youtube.com) Unterlagen von Leybold
hierzu: Versuchsanleitung als pdf Massenspektrometer Aufbau von Bainbridge (1932) Ziel eines Massenspektrometers ist es, die Masse von geladenen Teilchen zu bestimmen. Wir stellen hier zunächst den Aufbau von Bainbridge vor. Hierzu wird der Wienfilter mit einem zusätzlichen Magnetfeld erweitert, d.h. die geladenen Teilchen, die den Wienfilter mit definierter Ge- schwindigkeit verlassen, werden in ein weiteres Magnetfeld senkrecht eingeschossen und durchlaufen in diesem Magnetfeld einen Kreis- bogen, bis sie auf einem Schirm auftreffen. Das sieht dann also folgen- dermaßen aus:
Quelle: https://virtuelle-experimente.de/b-feld/anwendung/massenspektrometer.php Der Halbkreisdurchmesser „d“ kann gemessen werden und macht eine Aussage über die Masse des Teilchens. Es gilt:
Hinweis:
Falls man die Ladung q des Teilchens nicht kennt, ist nur die Bestimmung der spezifischen
Ladung q/m möglich. Aufbau von Bucherer (1908) In der Relativitätstheorie wurden mit dem Versuch von Bucherer auch Massen bestimmt. Diesen Aufbau sieht man hier:
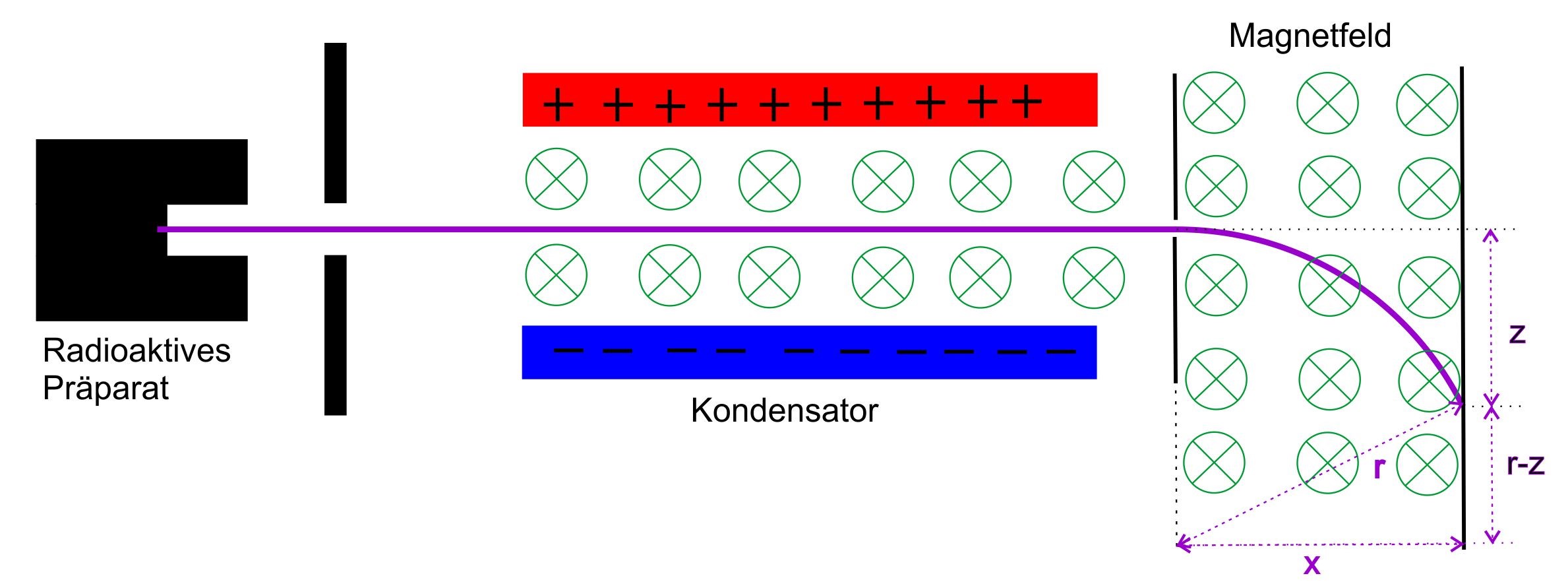
Hier wird kein vollständiger Halbkreis beschrieben, so dass die For- meln komplexer sind. Es gilt hier: (man geht im Allgemeinen von kleinen Werten für „z“ aus, d.h. in der
Abb. ist „z“ übertrieben groß eingetragen )
Aufbau nach Aston (1918) Danach entwickelte Francis William Aston einen Massenspektrometer, der vor allem zur Identifikation von Isotopen benutzt wurde. Hierzu gibt es eine schöne Simulation
im Netz:
Quelle: Leifi Dieser Aufbau besteht also aus einer Ionisationskammer mit einem Beschleunigungskondensator (links). In der Ionisationskammer wer- den die Proben durch den Beschuss mit schnellen Elektronen ionisiert. Danach werden diese Ionen im elektrischen Feld E1 des Kondensators auf eine Geschwindigkeit v0 beschleunigt. Diese beschleunigten Ionen werden senkrecht zum E-feld eines zweiten Kondensators mit der Feldstärke E2 eingeschossen. Dabei durchlaufen sie eine parabelförmige Bahn. Es liegt ein Ablenkkonden- sator vor. Nach dem Verlassen des Ablenkkondensators gelangen die Ionen in ein senkrecht stehendes B-Feld. Es wird eine Kreisbahn beschrieben. Am Schluss treffen die Ionen auf eine Photoplatte, auf der sie dann registriert werden. Es findet hier eine Doppelfokussierung statt, d.h. Ladungen mit gleicher spezifischer Ladung q/m aber geringen Geschwindigkeits- oder Richtungsunterschieden werden auf einem Punkt der Detektor- platte zusammengeführt. Hinweis:
Eine physikalische Betrachtung dieses Phänomens erscheint mir in der
Oberstufe nicht
angebracht. Ich gehe nur kurz beim Aufbau von Mattauch
darauf ein. Wer mehr
darüber erfahren will, sollte in der Linkliste unter
den PDF-Dateien nachsehen. Extrateil: Abhängigkeit von Ekin und p Häufig
findet sich in den Abhandlungen zum Massenspektrometer die Behauptung,
dass die Ablenkung im E-Feld von der kinetischen Ener- gie und die
Ablenkung im B-Feld vom Impuls abhängt. Dies lässt sich noch mit
relativ geringem Aufwand zeigen. Zur
Ablenkung im E-Feld gehen wir zurück zum
Ablenkkondensator: Es gilt:
Mit den
Formeln zum
Fadenstrahlrohr und zum Versuch von Bucherer ergibt
sich:
Da die
Ablenkungen im E- bzw. B-Feld in unterschiedlichen Richtun- gen
stattfinden, kann man durch eine geschickte Anordnung Fokussier- ungen auf
einer Detektorplatte erhalten. Aufbau von Thomson (1913) Schon
sehr früh stellte J.J.Thomson seine Form von einem Massen- spektrometer
vor. Man spricht von der Parabelmethode, weil Teilchen mit
gleicher spezifische Ladung q/m bei unterschiedlicher Geschwin- digkeit
einen Parabelbogen auf Photopapier bilden. Der
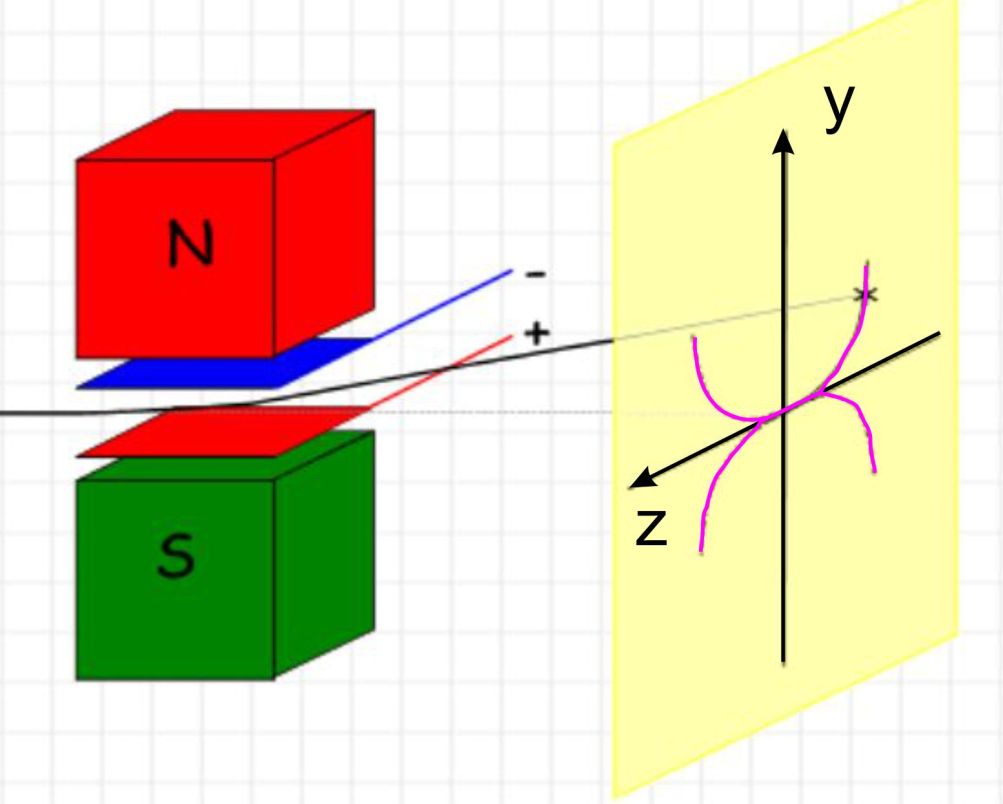
Aufbau hat folgendes Aussehen:
Mit kleinen Änderungen aus der
Quelle:
roro-Seiten Thomson Die
violetten Bögen zeigen Parabeln, die zur selben spezifischen Ladung
q/m gehören. Das
E-Feld und B-Feld nehmen denselben Raum in Anspruch und liegen
parallel zueinander. Die Ablenkung durch das E-Feld erfolgt in y-Richtung,
die Ablenkung durch das B-Feld in z-Richtung. Man kann
zeigen, dass y in Abhängigkeit von z eine quadratische Funktion
bildet, so dass ein Parabelbogen entsteht. Es gilt
nämlich (Extrateil):
Da sich
„z“ mit „v“ ändern kann, erhält man auf der Photoplatte
den Ausschnitt
eines Parabelbogens. Aufbau von Mattauch (1934) Bei
diesem Spektrometer handelt sich um ein typisches Beispiel für einen Sektorfeld-Massenspektrographen. Der Aufbau wird
häufig mit optischen
Aufbauten, wie Linse und Prisma, verglichen. Es finden also
Fokussierungen durch die Art des Aufbaus von elektrischem und magnetischem
Feld statt. Im Idealfall liegt eine Doppelfokussierung vor.
Häufig wird ein inhomogenes E-Feld mit einem homogenen B-Feld kombiniert.
Die Felder haben ganz genau vorberechnete Abmessun- gen. Im
Folgenden sieht man den Aufbau von Mattauch und Herzog.
Quelle: PDF zur Massenspektroskopie FH
München Ein
inhomogenes E-Feld (31,5°Sektor) wird kombiniert mit einem homogenen
Magnetfeld, bei dem die Lage des Flächendetektors genau
ausgerechnet wurde. Weitere Ausführungen Es gibt noch
weitere Ausführungen von Massenspektrometern, die aber
nicht zum Thema „E- und B-Felder“ passen. Man kennt noch den Quadrupol-
und Flugzeitdetektor.
Hierzu kann man sich die Verlink- ung mit
den wikipedia-Artikeln bzw. die PDF-Artikel in der
Linkliste an-sehnen. Linkliste
zum Massenspektrometer:
Zyklotron Das
Zyklotron zählt zu den Ringbeschleunigern. Hier werden geladene Teilchen
auf Spiralbahnen auf hohe Energien bzw. Geschwindigkeiten gebracht. Der Aufbau eines klassischen
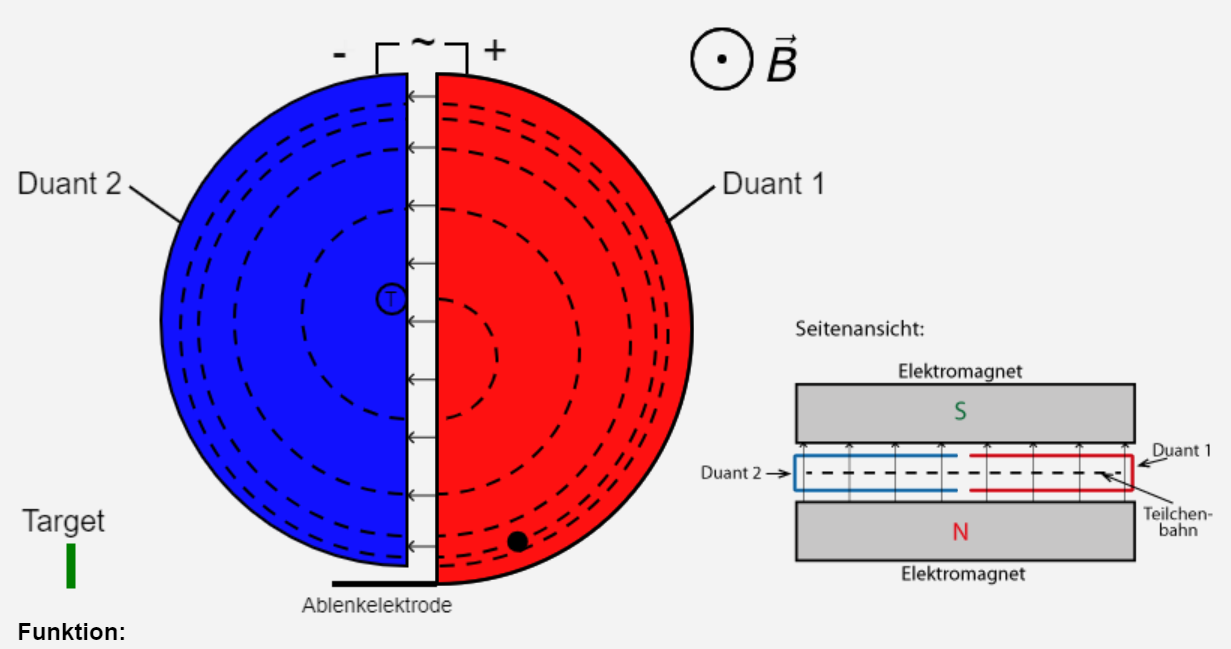
Zyklotrons hat folgendes Aussehen:
links: Aufsicht
rechts: Querschnitt Quelle: virtuelle
Physik In einer
großen Vakuumkammer befindet sich ein Aufbau aus zwei großen
hohlen Halbzylindern aus Metall (z.B. Kupfer, kein Eisen). Die
einzelnen Halbzylinder werden Duanten oder einfach
„Dees“ ge- nannt,
weil sie das Aussehen des Buchstabens „D“ haben. Da die
Zylinder hohl sind, bilden sie Faradaykäfige,
d.h. im Inneren existiert
kein elektrisches Feld, obwohl sie geladen werden. Nur im Raum
zwischen den Duanten kann sich ein E-Feld
ausbilden. Der
ganze Aufbau wird von großen Elektromagneten umgeben, die den
gesamten Innenraum ausfüllen. In der
Duantenmitte befindet sich eine Ionenquelle, die geladene Hier die
Abbildung eines historischen Zyklotrons:
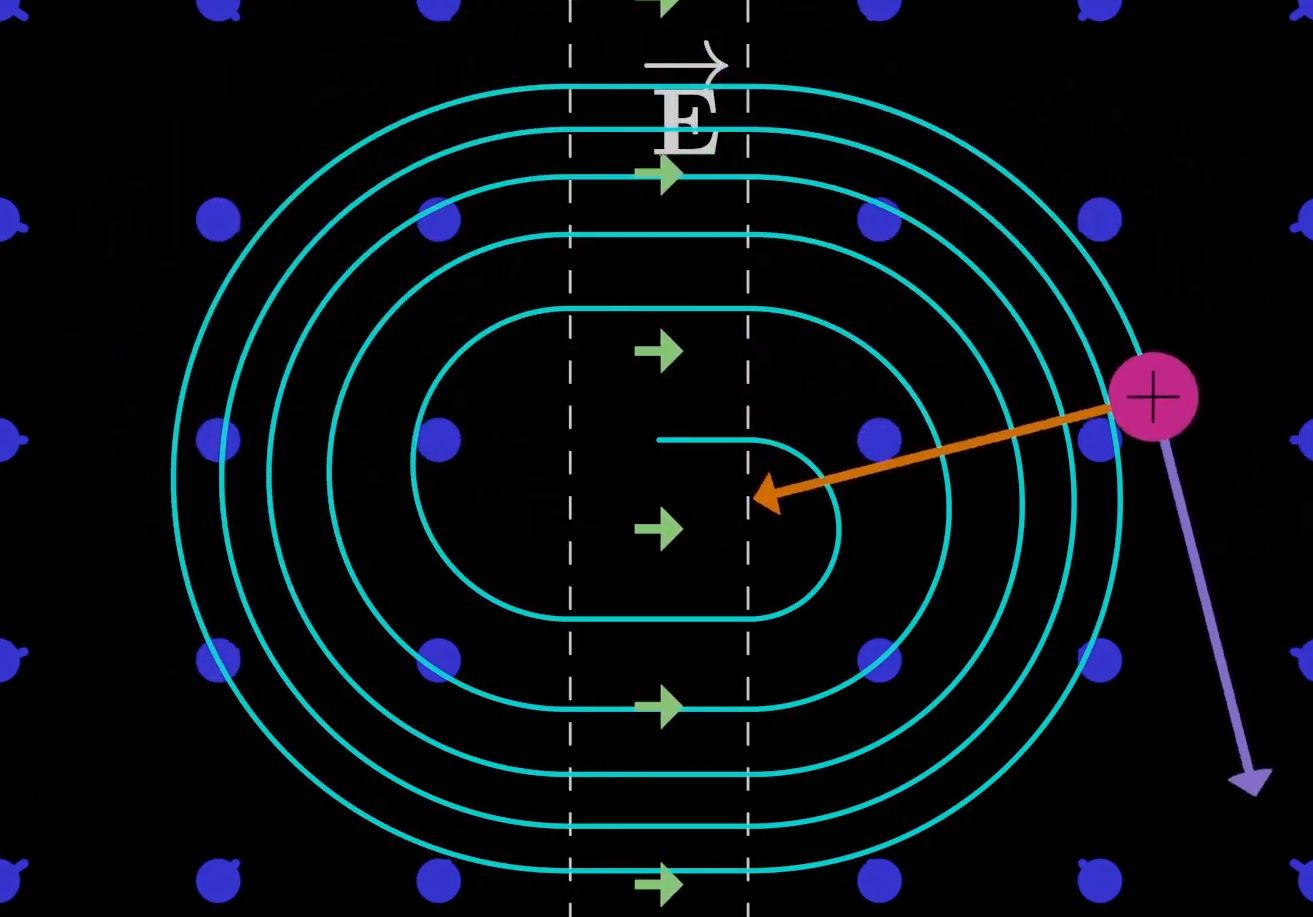
Funktion: Da bewegte
geladene Teilchen vorliegen,
können beide Felder auf diese
einwirken. Im Raum zwischen den Duanten werden die
Teilchen durch das
E-Feld beschleunigt. Das Magnetfeld führt zu Halbkreis- bahnen innerhalb der Duanten. Da man den Ladungszustand der Duan- ten
laufend wechselt (Wechselfrequenz), kann immer im Duanten-zwischenraum beschleunigt werden. Die Frequenz muss natürlich auf die Teilchenbewegung abgestimmt sein. Da die Geschwindigkeit der Teilchen zunimmt, wird auch der Radius der Halbkreisbahnen größer, so dass die Teilchen sich auf einer „Spiralbahn“ bewegen. Wenn sie den Rand der Anordnung erreichen, werden sie über das zusätzliche elektrisches Feld einer Elektrode abgelenkt und aus dem Aufbau auf ein Ziel
(Target) geführt. Die Wechselfrequenz kann im Zyklotron konstant gehalten werden (s. Formeln) Formeln: In den
Kapiteln zum Fadenstrahlrohr
und zur Schraubenbahn
findet man die
Formeln, die man hier benötigt.
Man
erkennt, dass „T“ bzw. „f = 1/T“ unabhängig
von „v“ ist. Allerdings besteht
eine Abhängigkeit von „m“. Solange also „m“ konstant ist, ist die Umlaufdauer
immer gleich. Ein Problem ergibt sich
bei Geschwindigkeiten v > 0,1∙c, weil dann relativistisch
gerechnet werden müsste (s.
relativistische Masse (in Arbeit)) Die
Masse nimmt dann merklich zu, die Frequenz ändert sich und müsste
nachgesteuert werden. Man spricht dann von einem Synchro- zyklotron.
Dieses Gerät kann nicht kontinuierlich betreiben werden, da sich
dann ja Massen mit unterschiedlichen Geschwindigkeiten im Ge- rät
befinden. Man kann also nur einzelne Massepakete untersuchen. Man
spricht von einem Pulsbetrieb. Beispielrechnung
für vmax:
Man
erkennt, dass nur bei schweren Ionen keine relativistische Rechnung
nötig ist (ab
v ≈ 0,1∙c muss relativistisch gerechnet werden). Daher
werden im Allgemeinen nur schwere Ionen in einem Zyklotron beschleunigt. In der
folgenden Rechnung wird noch einmal gezeigt, dass es keinen Sinn macht, Elektronen im Zyklotron zu
beschleunigen. Außerdem wird
berechnet, in welcher Größenordnung (Angabe
meist in MeV) die maximalen
Energien liegen.
Hier
drei Videos in englischer Sprache zur Funktion des Zyklotrons.
Hinweis: das Video von „physikdigital“ und die Animation
bei „Leifi“ bringen meiner Meinung nach nichts Neues. Anwendung in der Medizin 1.) Diagnostik:
PET-Verfahren Die Positronen-Emissions-Tomographie
(PET) wird vor allem in der Diagnostik
von Krebserkrankungen benutzt. Man untersucht hierzu den
Zerfall von Positronen
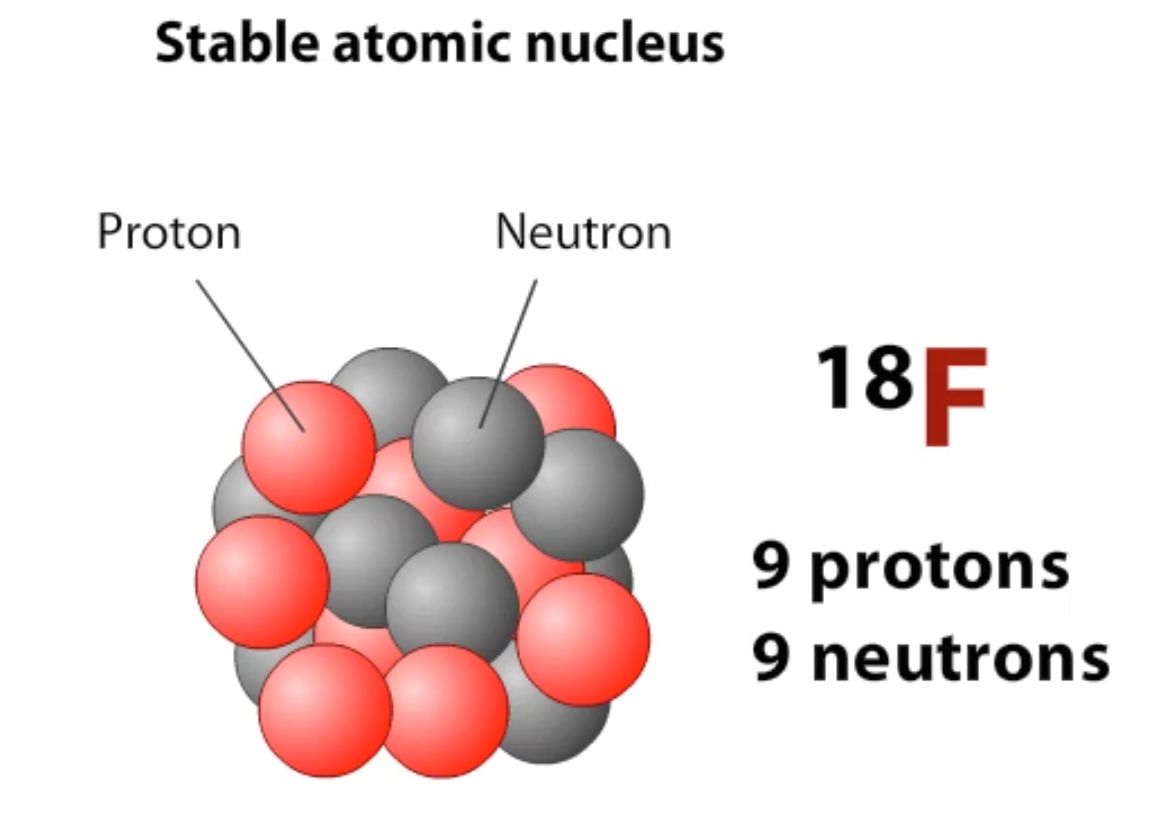
eines Radionuklids,
meist 18Fluor. Dieses Radionuklid
wird durch Beschuss von 18O durch beschleunigten Pro- tonen
erzeugt. Diese beschleunigten Protonen stammen aus einem Zyklotron. Hinweis: Für ein vertieftes Verständnis der ablaufenden
Prozesse braucht man Kenntnisse aus der Kernphysik (s. Videoliste.1.Video) 2.) Therapie:
Protonentherapie Die Protonentherapie
wird vor allem bei tief im Körper sitzendem bös- artigem
Krebsgewebe zur Behandlung benutzt. Der Krebs wird dabei zielgenau
mit Protonen beschossen. Die energiereichen Protonen stammen
aus einem Zyklotron (Synchrozyklotron) oder sogar Synchrotron (s. nächstes
Kapitel). Hierzu
eine Auswahl von Videos:
Synchrotron Im Gegensatz
zum Zyklotron durchlaufen die Teilchen in einem Syn- chrotron
keine Spiralbahnen, sondern „Kreisbahnen“ mit
festem Ra- dius. Da aber bei der Beschleunigung die Geschwindigkeit
der Teilchen zunimmt,
kann hier das B-Feld nicht konstant sein, sondern muss immer
stärker werden, damit sich der Radius nicht verändert. Man muss
eine Synchronisation zwischen der
Teilchengeschwindigkeit und der Feldstärke vornehmen. Daher der Name des Ringbeschleunigers als
„Synchrotron“. Damit die magnetische Feldstärke nicht übermäßig hohe
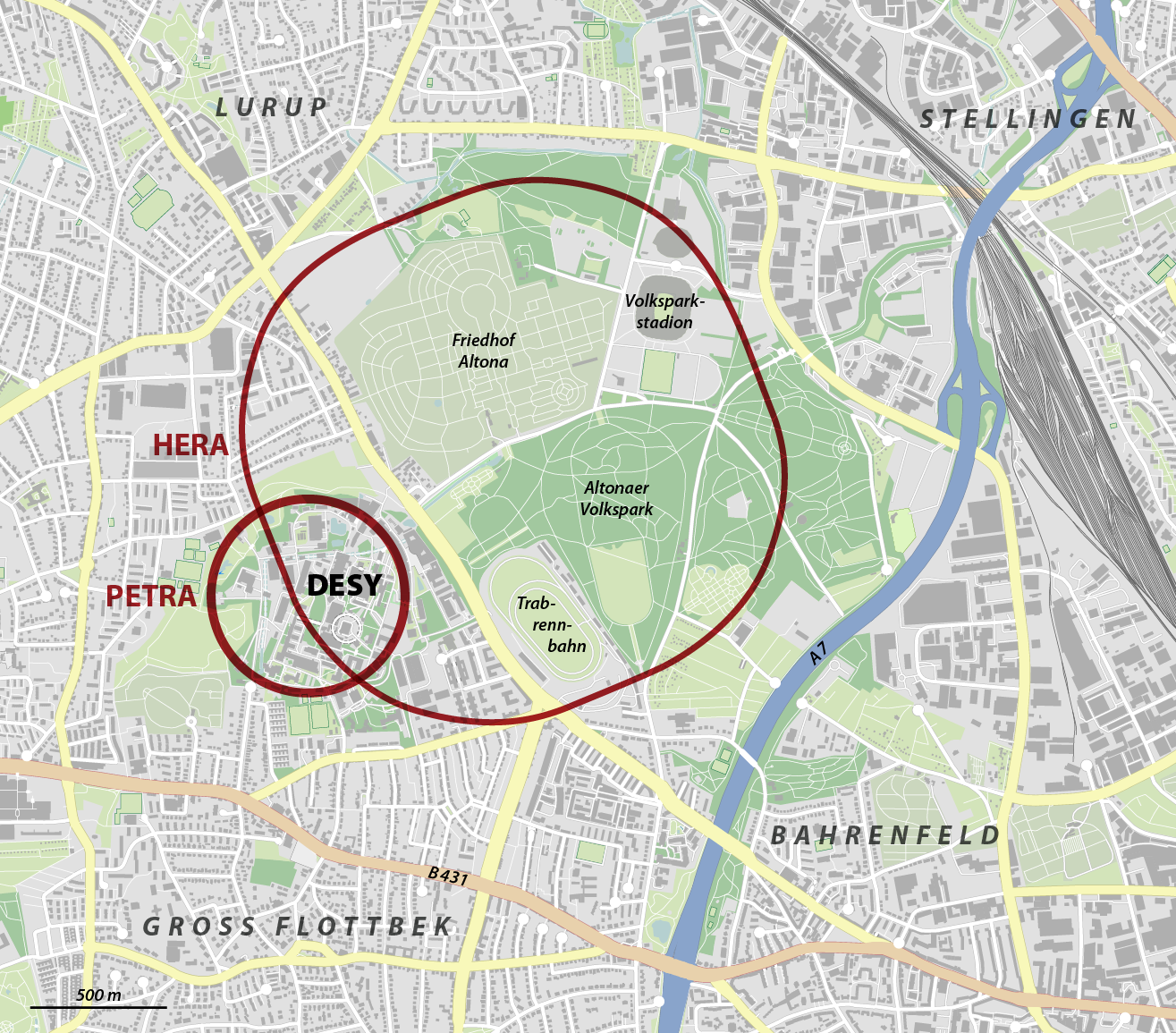
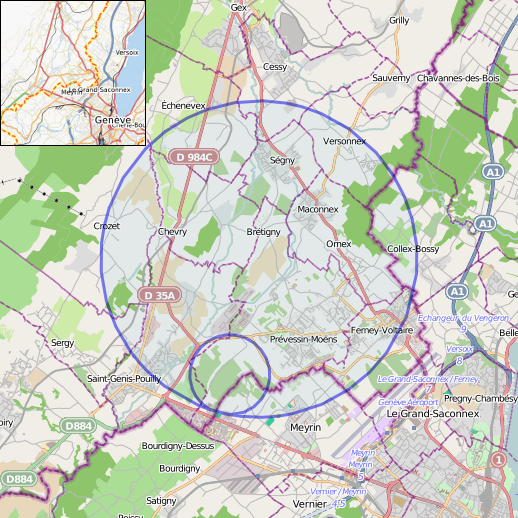
Werte erreicht, muss der Radius solcher Beschleuniger ziemlich groß sein. Beim DESY-HERA z.B. fast 1 km, beim LHC sogar ca. 4,3 km.
Da der Ringbeschleuniger aber keine ideale Kreisform hat, wird
häufiger nur der Umfang angegeben, also DESY-HERA 6,336 km und beim
LHC 26659 km. Hier
einmal Bilder zu den Abmessungen der beiden Beschleuniger: Im
Wesentlichen besteht das Synchrotron aus Teilen, die zur
Be- schleunigung
dienen, also mehreren E-Feldern, und Teilen zur Ab- lenkung, also
mehreren B-Feldern. Eine Wechselspannung polt die elektrischen
Felder immer so, dass eine Beschleunigung gerade beim Eintritt
in das Feld stattfindet. Auch diese Frequenz muss der Ge- schwindigkeit
angepasst werden. Außerdem treten bei den hohen Ge- schwindigkeiten auch relativistische Effekte auf, die ebenfalls Berück- sichtigung
finden müssen. Es geht also im Synchrotron auch viel um die richtige Steuerung von
E- und B-Feld. Die
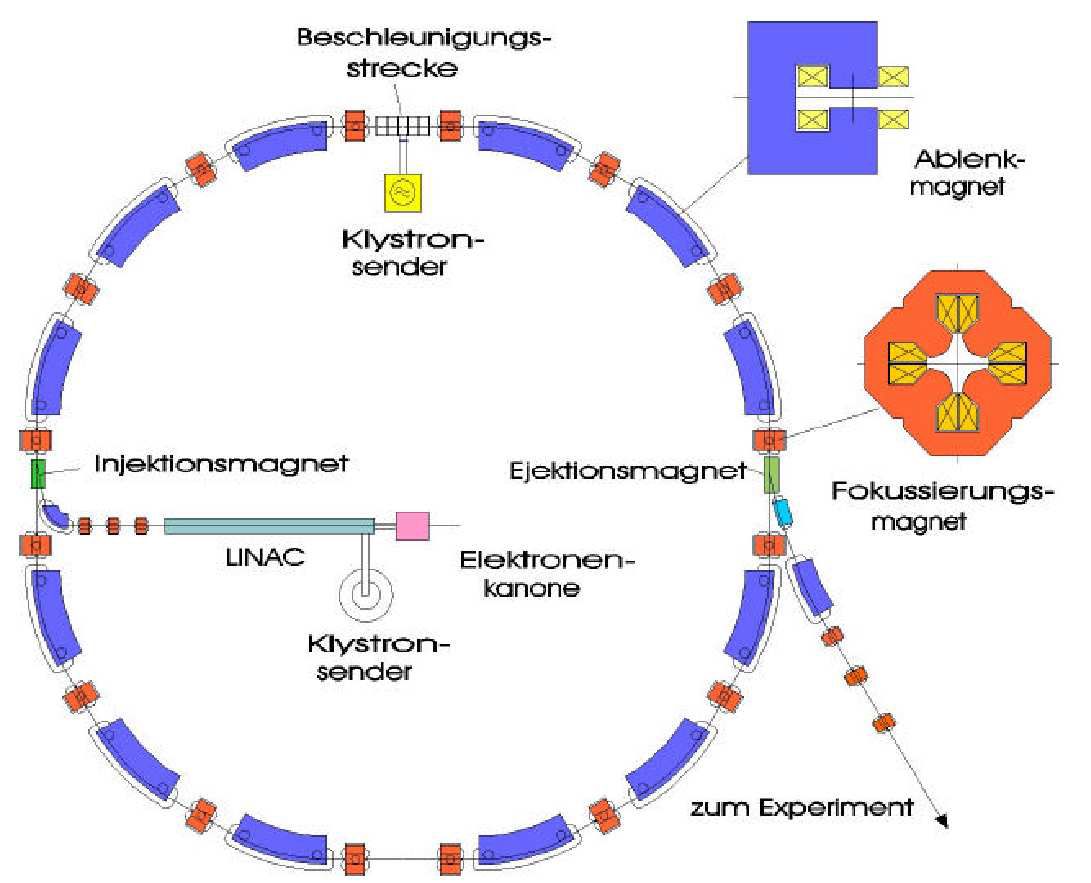
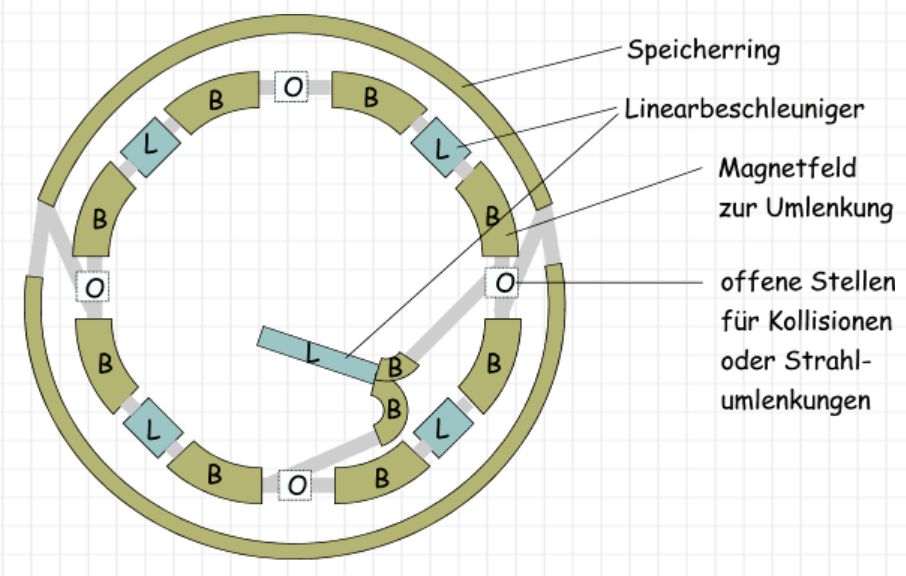
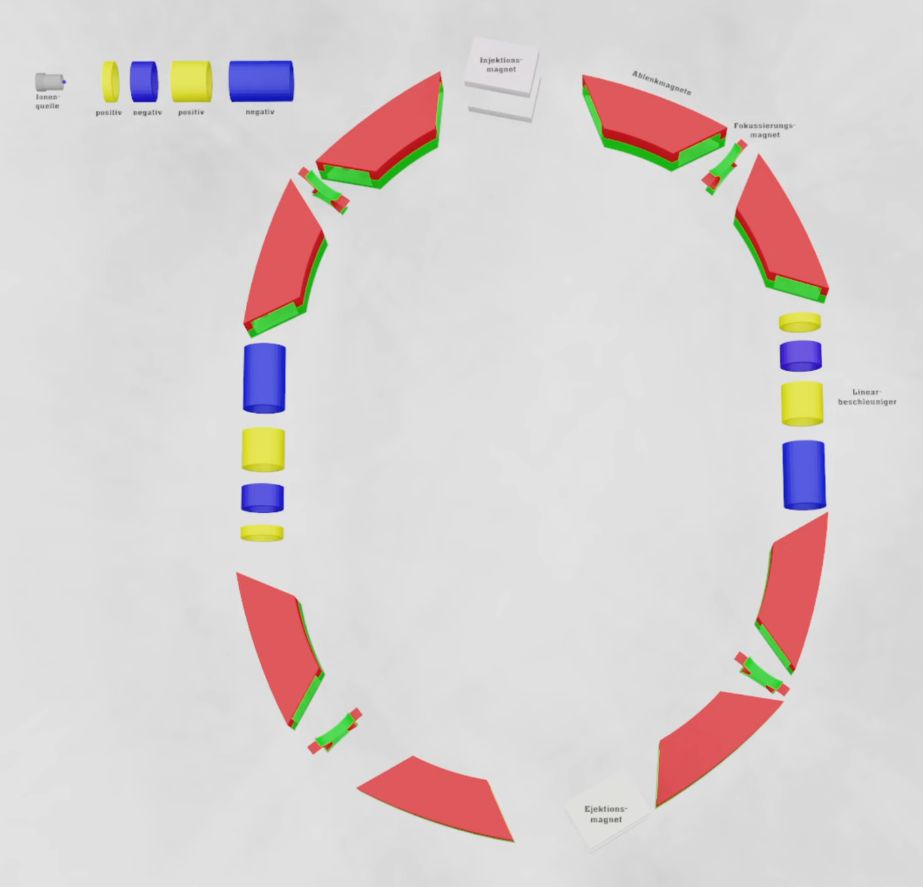
folgenden Abbildungen zeigen einmal schematisch den Aufbau.
Es gibt
lineare Beschleunigungsstrecken (Linearbeschleuniger),
kombiniert
mit Ablenkmagneten und Fokussierungsmagneten. In der
Regel sind die Teilchen, die in das Synchrotron gelangen, schon vorbeschleunigt, meist durch einen großen Linearbeschleuniger. Kurz zum
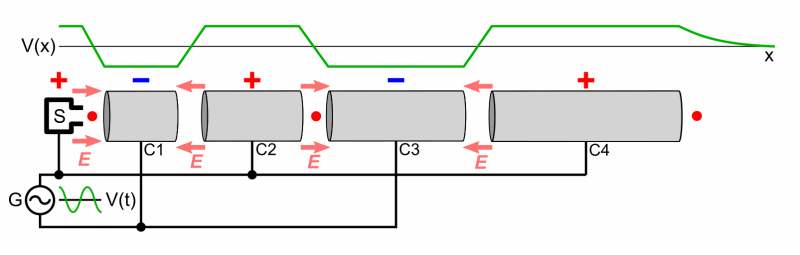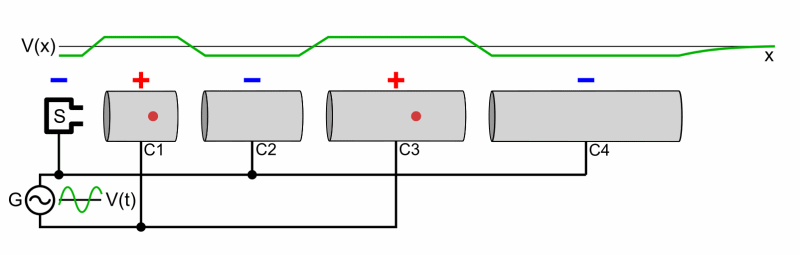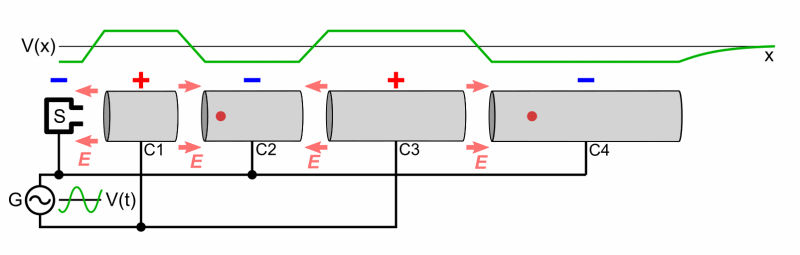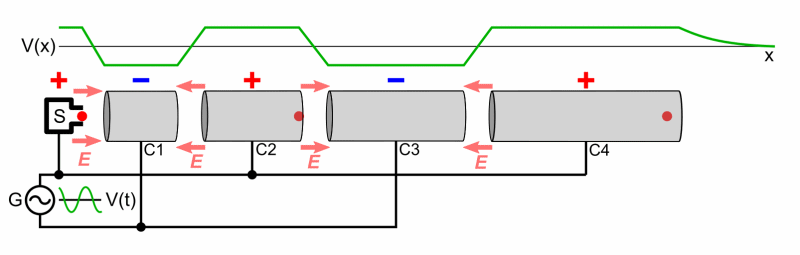
Aufbau eines Linearbeschleunigers. Er besteht im Prinzip aus
aneinandergereihten Kondensatoren. Im elektrischen Feld dieser Kondensatoren
findet dann die Beschleunigung statt. Die anliegende Frequenz
muss entsprechend abgestimmt sein. Die
folgende Abbildung zeigt einmal schematisch den Aufbau:
Quelle: wikipedia Die Kondensatoren
bilden die Enden von „Driftröhren“, in denen sich die
Teilchen feldfrei (Faraday-Käfig)
mit konstanter Geschwindigkeit bewegen.
Nur im Raum zwischen den Driftröhren wird beschleunigt. Bewegt
sich das Teilchen innerhalb der Driftröhre, kann die Spannung der
Röhre durch die anliegende Frequenz geändert werden. Bleibt, wie in
diesem Fall, die Frequenz konstant, muss die Länge der Drift- röhren
aufgrund der erhöhten Geschwindigkeit immer größer werden, damit
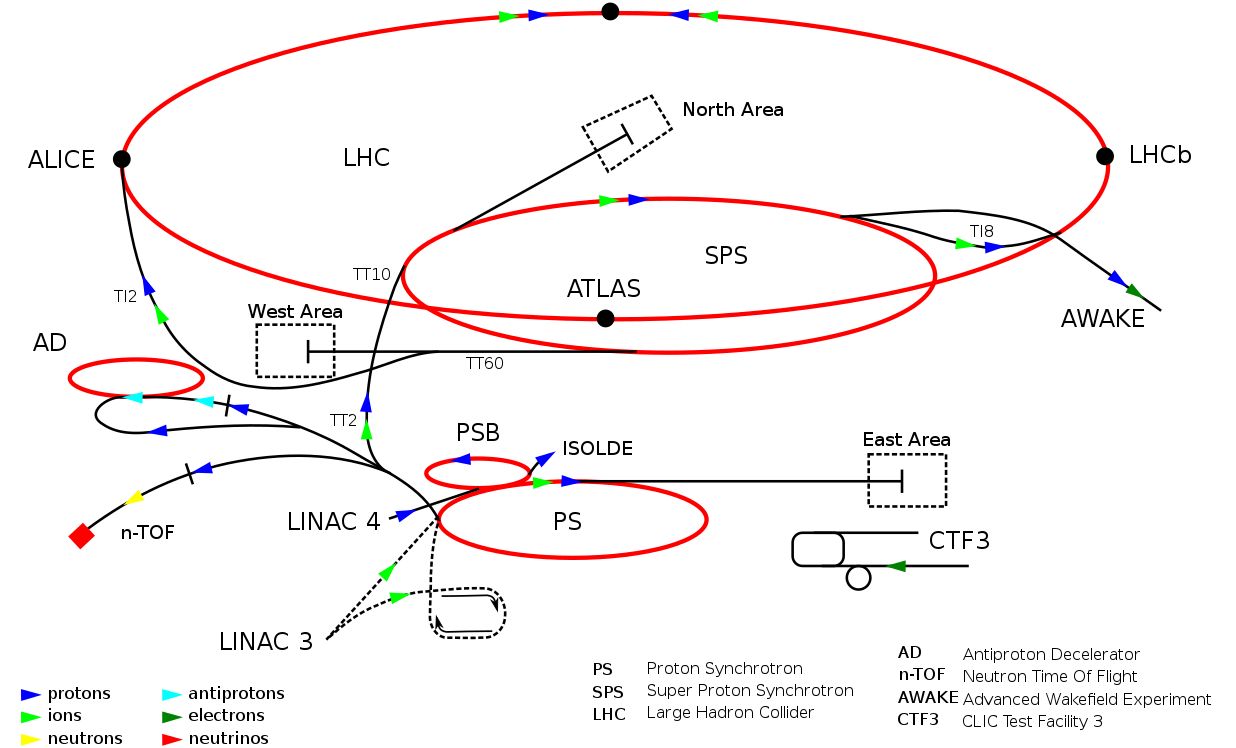
die Zeit zur Umpolung zur Verfügung steht. Eine große Beschleunigeranlage, wie das CERN, kann aus sehr vielen Linear- und Ringbeschleunigern bestehen, wie folgendes Bild zeigt:
Quelle:
wikipedia Hier zwei YouTube-Videos von der Plattform „physikdigital“ zum Thema:
Linkliste zum Thema „Beschleuniger“:
zurück
zum Abschnitt:
zurück
zu vorherigen Kapiteln
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||