Fadenstrahlrohr − Messungen

Rückblick

In diesem Kapitel soll es um Messungen gehen, die mit dem Fadenstrahlrohr möglich sind. Wir werden die Formel zur Lorentz-

kraft bestätigen, die wir ja theoretisch hergeleitet hatten. Am Schluss

soll aber vor allem zentral die Bestimmung der Elektronenmasse

stehen.

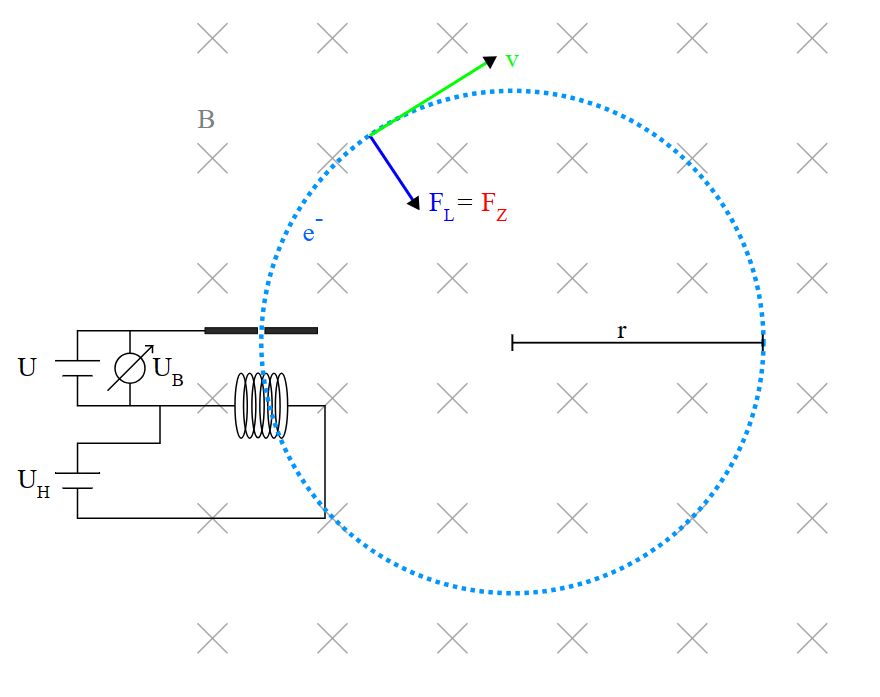
Aus dem Kapitel „Fadenstrahlrohr“ wissen wir, dass sich die Elektron-en im Fadenstrahlrohr(+Helmholtz-Spule) auf Kreisbahnen bewegen, wenn die Elektronen senkrecht zum Magnetfeld eingeschossen

werden. Folgende Abbildungen noch einmal zur Erinnerung:

Fadenstrahlrohr mit Helmholtzspule

Abb aus der Quelle: https://lp.uni-goettingen.de/get/text/1545

Abbildung zu der Lorentzkraft als Radialkraft

Quelle: https://de.wikipedia.org/wiki/Fadenstrahlrohr

Da die Lorentzkraft nach der Drei-Finger-Regel immer senkrecht zur

Geschwindigkeitsrichtung („technische Stromrichtung“) verläuft, ergibt

sich, dass die Lorentzkraft in diesem Fall als Radialkraft bzw. Zentri-

petalkraft wirkt.

Hinweis: Bei Elektronen muss der Daumen bei der Drei-Finger-Regel entgegengesetzt zur

Elektronenrichtung zeigen oder man nimmt die linke Hand.

Bestätigung der Formel für die Lorentzkraft

Im dem vorherigen Kapitel „Bewegte Ladungen im Magnetfeld“ haben

wir eine Formel für die Lorentzkraft hergeleitet, die lautete:

Dies bedeutet, dass die Lorentzkraft proportional zu v sein muss, also

je größer v ist, um so größer ist auch die Lorentzkraft.

Um dies nachzuweisen, müssen wir für die Größen v und F Größen

wählen, die zu diesen proportional sind.

Die Herleitung dieser Größen erfolgt aus zwei bekannten Zusammen-

hängen.

1.) In der Elektronenkanone ergibt sich die kinetische Energie der

Elektronen aus der an den Elektronen im E-Feld verrichteten Arbeit.

2.) Wir kennen eine Formel für die Radialkraft aus der Kreisbewegung.

Wir haben also:

Mit folgendem Versuchsaufbau wurden von mir diese Messungen

durchgeführt:

Es ergaben sich folgende Messwerte (LK 98/99):

[U wird direkt am Voltmeter abgelesen, den Radius kann man an einer Skalenleiter im Glas-

kolben messen]

U in V	55	85	120	162	220	275	340
r in cm	2	2,5	3	3,5	4	4,5	5

Hieraus berechnet man die gesuchten Größen.

	7,4	9,2	10,9	12,7	14,8	16,6	18,4
U/r	27,5	34	40	46	55	61	68

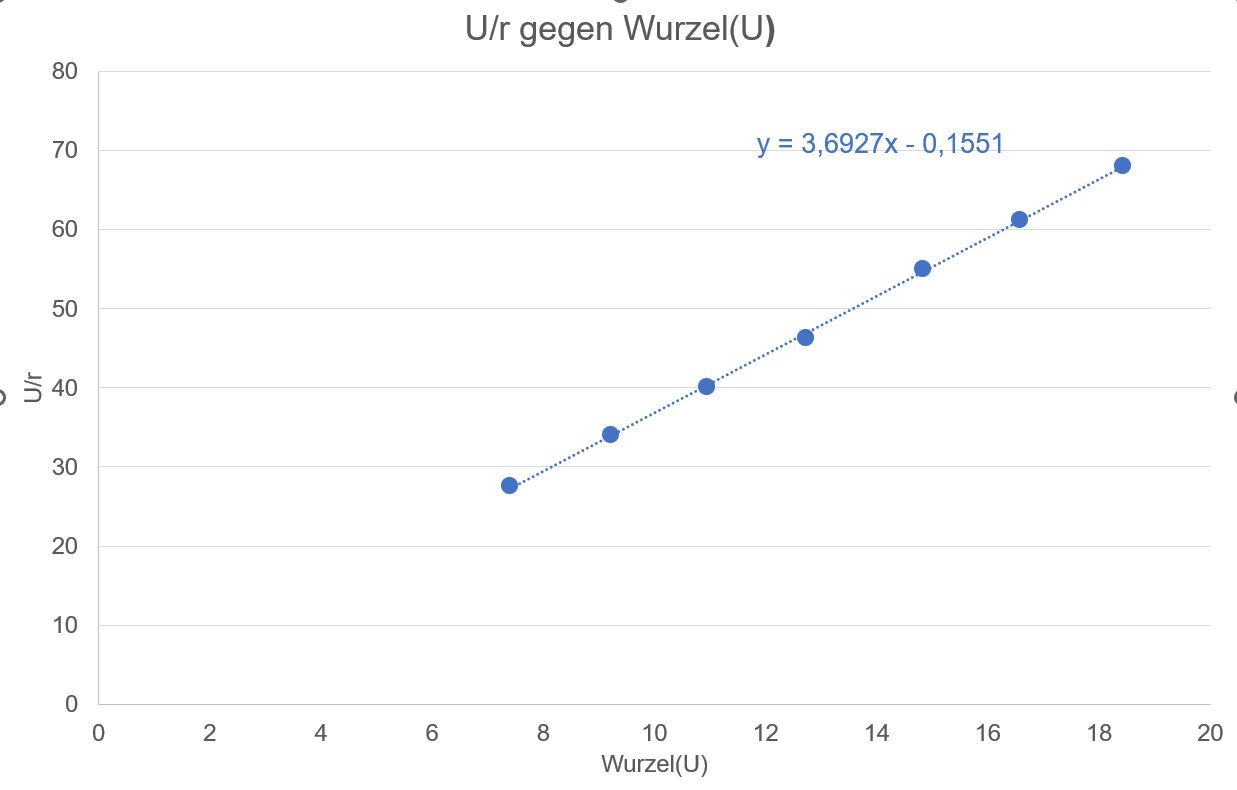
Die Auswertung mit Excel ergibt:

Da eine Ursprungsgerade als Trendlinie zu erkennen ist, ist also der

Zusammenhang zwischen F und v bestätigt, da „U/r“ proportional zu

„Wurzel U“ ist.

Mit den vorhandenen Messwerten kann man auch noch weitere Zu-

sammenhänge nachprüfen, z.B. den Zusammenhang zwischen r

und v.

Hier gehen wir von der Formel für die Lorentzkraft aus (s. erster Teil

der Auswertung) und setzen diese Formel gleich mit der Formel für

die Radialkraft.

Es gilt:

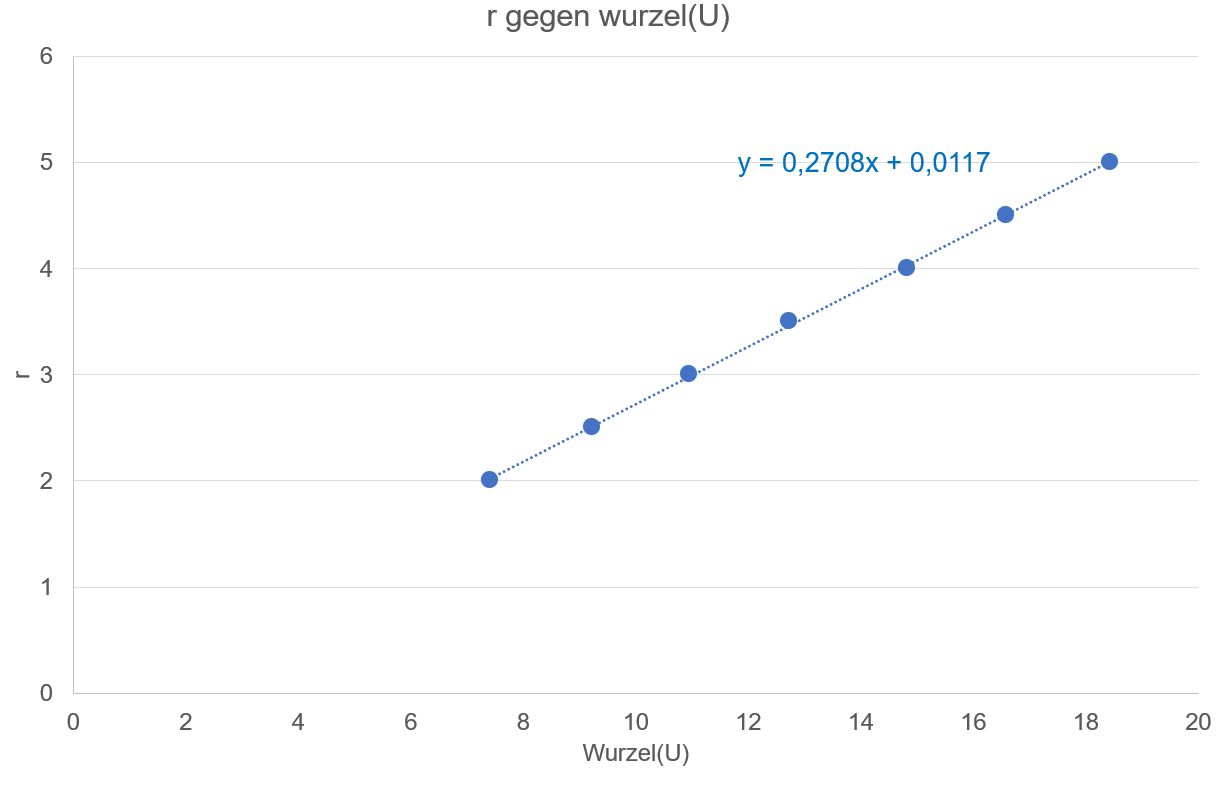
Wir benutzen die Messwerte von oben und werten mit Excel aus.

Die Beziehung wird also bestätigt, d.h. je kleiner der Radius ist, um

so kleiner ist auch die Geschwindigkeit. Dies zeigen die Messwerte

eindrücklich, da eine größere Spannung eine größere Geschwindig-

keit v bedeutet (wegen s. oben: 1.Zusammenhang).

Man kann also jetzt aus dem Radius der Kreisbahn auf die Ge-

schwindigkeit schließen, wie wir es bei dem Positronenbild getan haben.

Bestimmung der Elektronenmasse

Wir kommen jetzt zur zentralen Messung mit dem Fadenstrahlrohr.

Wir wollen nämlich hiermit die Elektronenmasse bestimmen.

Man geht dazu auf die schon bekannten Zusammenhänge zurück (s.o)

1. Zusammenhang:

kinetische Energie = verrichtete Arbeit des E-Feldes

2. Zusammenhang:

Lorentzkraft = Radialkraft

Hieraus ergibt sich durch Umstellungen eine Formel für m.

Er ergibt sich:

Wenn wir die obigen Messwerte benutzen, müssen wir jetzt noch den

Wert für B kennen. Das Problem ist, dass wir hier noch kein Mess-

verfahren haben, da dies erst im Kapitel „Halleffekt“ (noch in Arbeit) erklärt wird.

Nach der Betriebsanleitung von Phywe für die Helmholtz-Spule lässt

sich ein Richtwert von 0,62 mT/A berechnen (s. auch alte Phywe-Versuchs-

einheiten Atomphysik A 1.2.5). In unseren Fall betrug der Spulenstrom 2 A,

so dass B = 1,24 mT sein müsste.

Nehmen wir diesem Wert an, erhält man bei den obigen Messwerten

folgende Ergebnisse für m.

r in cm	2	2,5	3	3,5	4	4,5	5
m in 10⁻³¹ kg	8,95821	9,05701	9,23815	9,31418	8,95821	9,07018	9,05701

Dies ergibt im Mittel einen Wert von m = 9,09328 ∙ 10⁻³¹ kg, was ziem-

lich nahe an dem Literaturwert liegt (99,8 %).

Es gilt nämlich:

Die Ruhemasse eines Elektrons beträgt

m_e = 9,109 383 7015(28) · 10⁻³¹ kg

Quelle: https://de.wikipedia.org/wiki/Elektron

Wer noch einmal ein Video zum Fadenstrahlrohr sehe möchte, kann

sich diesen Ausschnitt aus einem Video von Benno Köhler ansehen.

(er geht sehr ausführlich auf den Aufbau (altes Leybold-Gerät) ein, es wird „r“ in Abhängigkeit von „B“ und „U“ gezeigt, leider sehr wenige Messungen, dafür sehr schöne Fotos von der Kreisbahn)