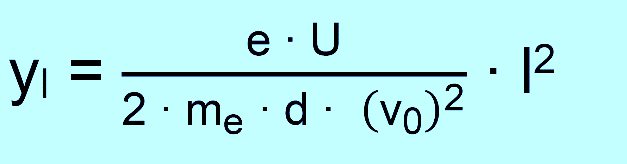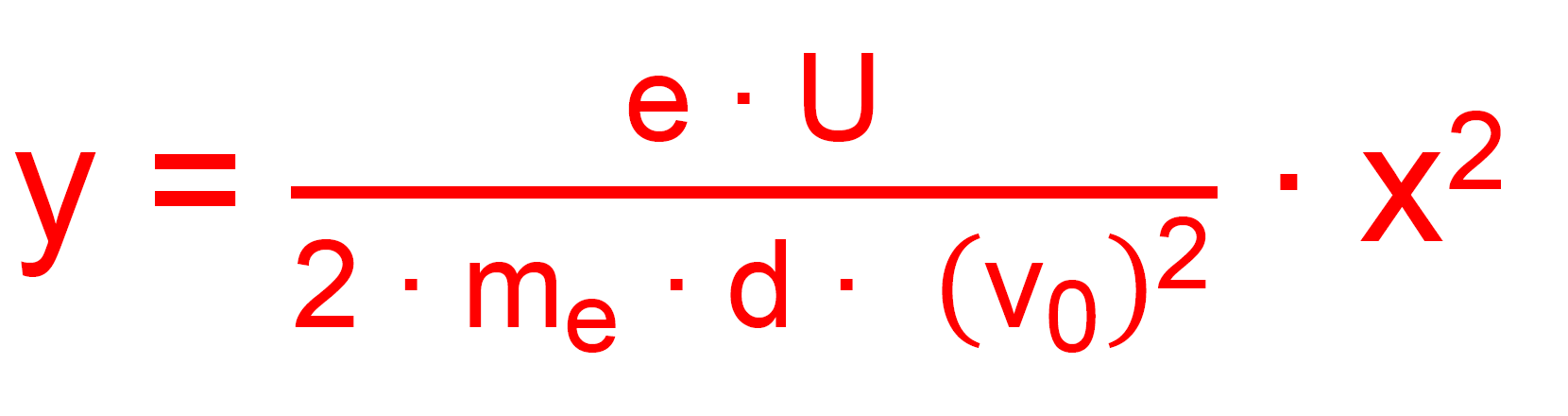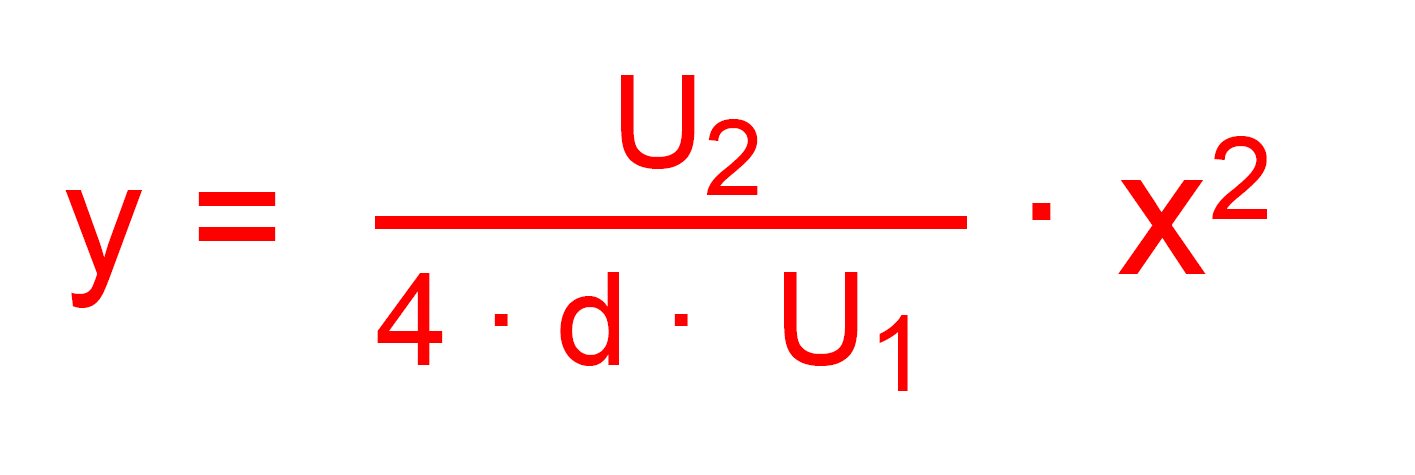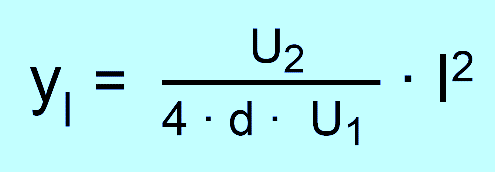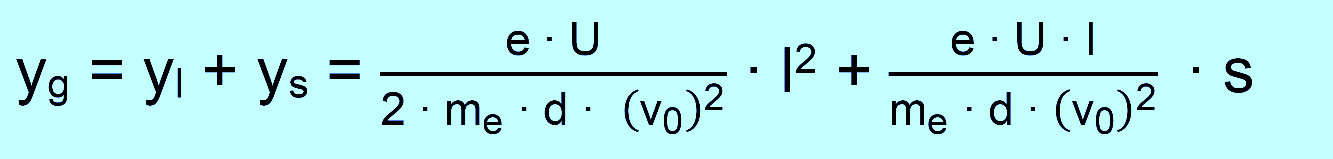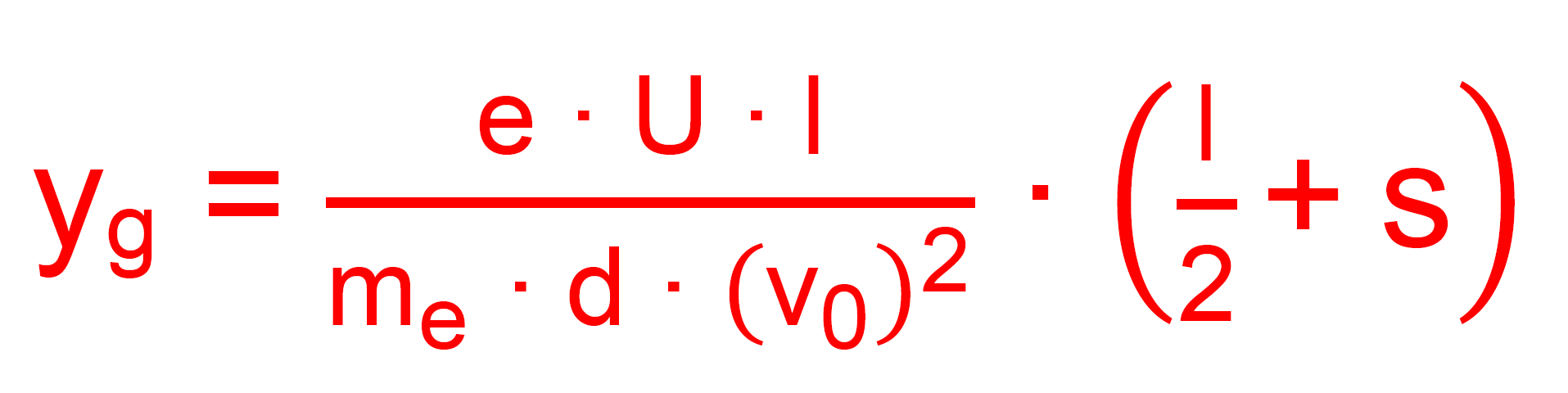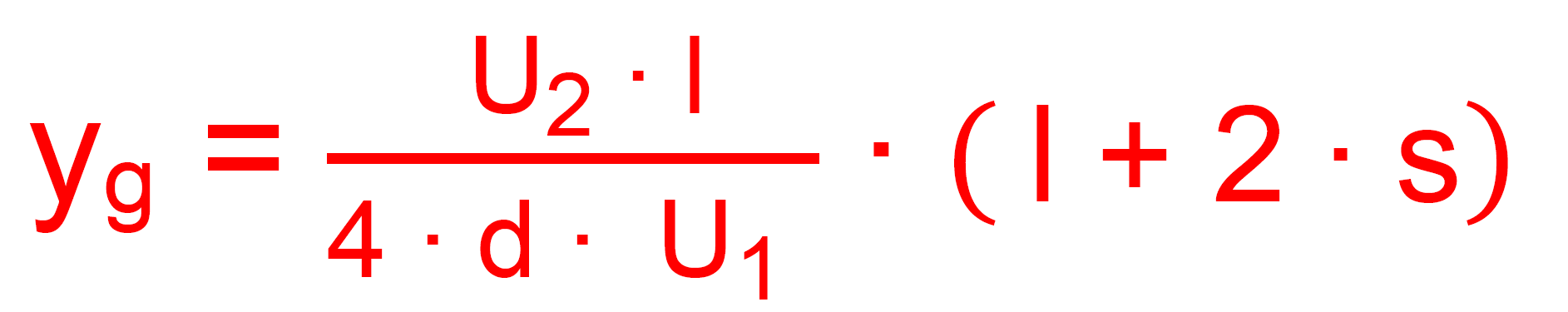Ablenkkondensator

Aufbau

Bisher wurde die Bewegung von Ladungen in einem Kondensator

immer aus der Ruhe heraus betrachtet, d.h. die Ladungen tauchen

plötzlich im Kondensator auf und man untersuchte die Bewegung

dieser am Start (t= 0 s) ruhenden Ladungen.(s. Übungsaufgaben)

Diesmal sollen die Ladungen schon in Bewegung sein, wenn sie

in den Kondensator gelangen. Es werden dabei praktisch immer

Elektronen betrachtet. Die Situation wird in folgender Abbildung

dargestellt.

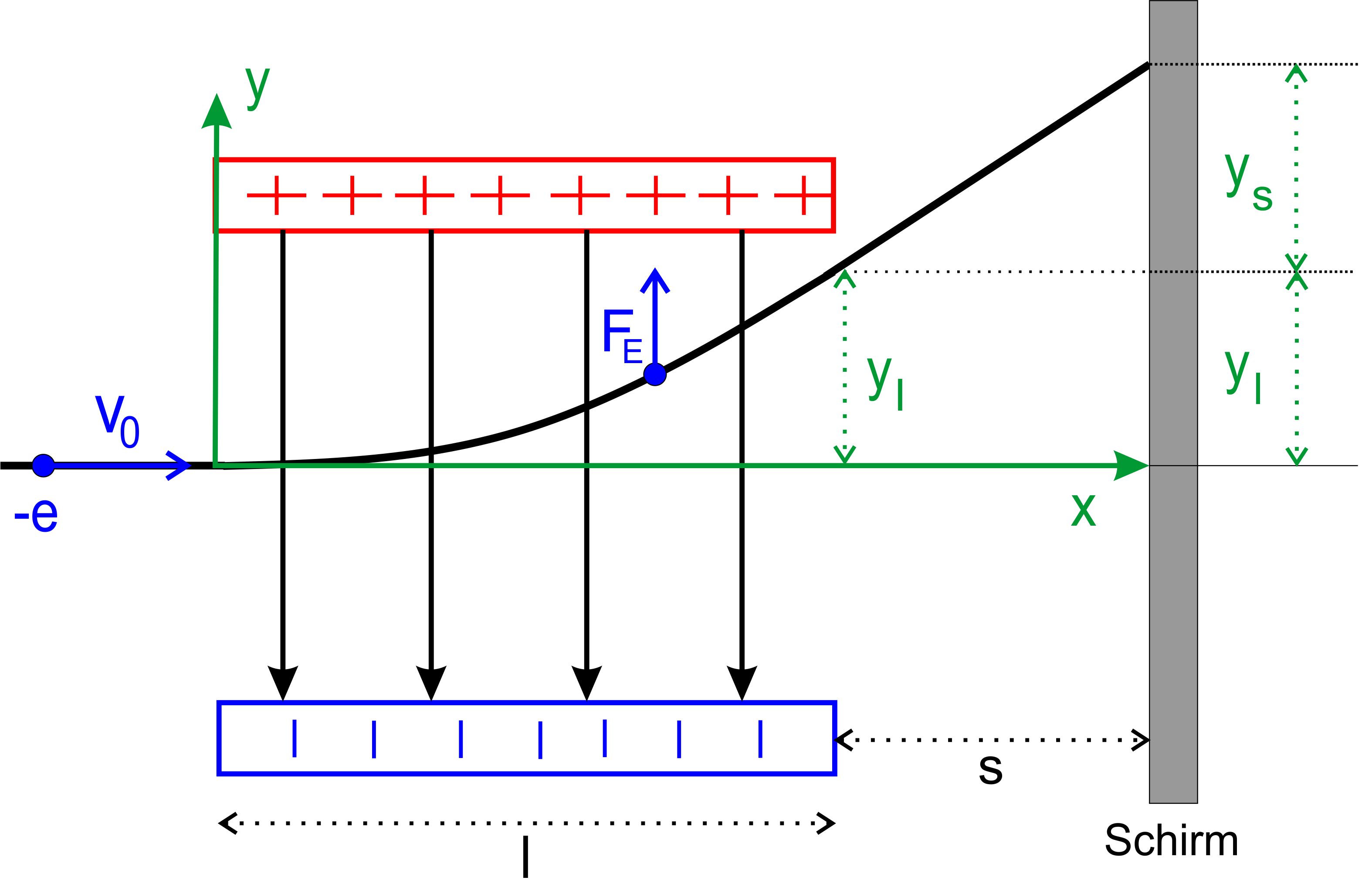
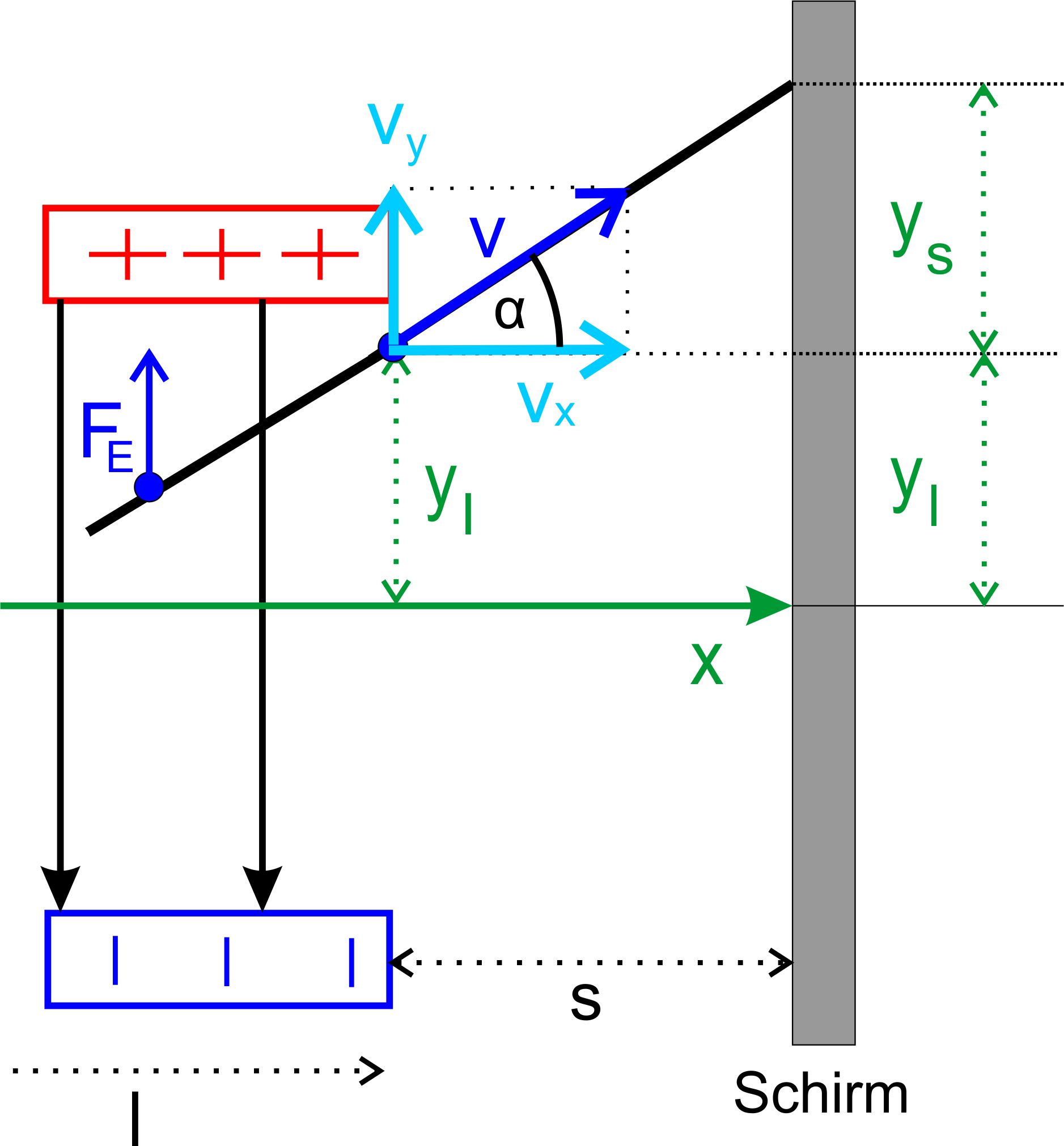
Die Elektronen kommen von links mit der Geschwindigkeit v₀ und

werden senkrecht zu den Feldlinien in den Kondensator „eingeschos-sen“. Im Kondensator erfahren sie eine Ablenkung durch die auf-

tretende elektrische Kraft F_E. Nach der Strecke l verlassen die

Elektronen den Kondensator und treffen nach einer Strecke s auf

einem Schirm auf, wo sie sich durch einen Lichtfleck bemerkbar

machen.

Analyse der Bewegung

im Kondensator

Wir wollen jetzt die Bewegung im Kondensator genauer betrachten.

Es besteht übrigens eine große Ähnlichkeit zum „waagerechten Wurf“.

Es liegt mal wieder das Superpositionsprinzip vor.

Man stellt sich ein Koordinatensystem im Kondensator vor (s.Abb.).

Der Ursprung liegt beim Eintrittspunktes des Elektrons in den Konden-

sator.

Die Kraft F_E wirkt senkrecht zur horizontalen Bewegungsrichtung, der

x-Richtung.

Hinweis: Das elektrische Feld soll nur auf den Plattenkondensator beschränkt sein, also nicht nach außen ausgreifen.

Für die x-Richtung gilt also:

Es liegt eine gleichförmige Bewegung vor, da keine Kraft in diese

Richtung einwirkt, somit gilt

x = v₀ ∙ t ; v_x = v₀ = konstant; a_x = 0 m/s²

Für die y-Richtung gilt:

Es liegt eine gleichmäßig beschleunigte Bewegung vor, da F_E wirkt

und diese Kraft konstant ist.

Somit gilt hier:

y = ½ ∙ a_y ∙ t² ; v_y = a_y ∙ t ; a_y = konstant

Man ist an der Bahnkurve im Plattenkondensator interessiert.

Für die y-Richtung gilt ja:

Dies ist eine Bewegungsgleichung, weil y in Abhängigkeit von t be-

rechnet wird.

Bei der Bahnkurve brauchen wir y in Abhängigkeit von x.

Wir ersetzen zunächst t in y(t) durch einen Term mit x.

Weitere Betrachtungen zu „a“.

Grundgleichung der Mechanik:

Ablenkung am Ende des Kondensators x = l

Wir halten fest, dass die Bahnkurve einer Parabel entspricht und für

die Berechnung von y(x) gilt:

Ablenkung im Kondensator 1

mit

e = Elementarladung (Elektron, Proton), sonst „q“ wählen

U = Spannung am Ablenkkondensator

m_e = Masse des Elektrons; sonst Masse von „q“

d = Abstand der Platten

v₀ = Eintrittsgeschwindigkeit

Berücksichtigung der Beschleunigung

Bisher wurde nicht darüber gesprochen, wie die Elektronen eigentlich

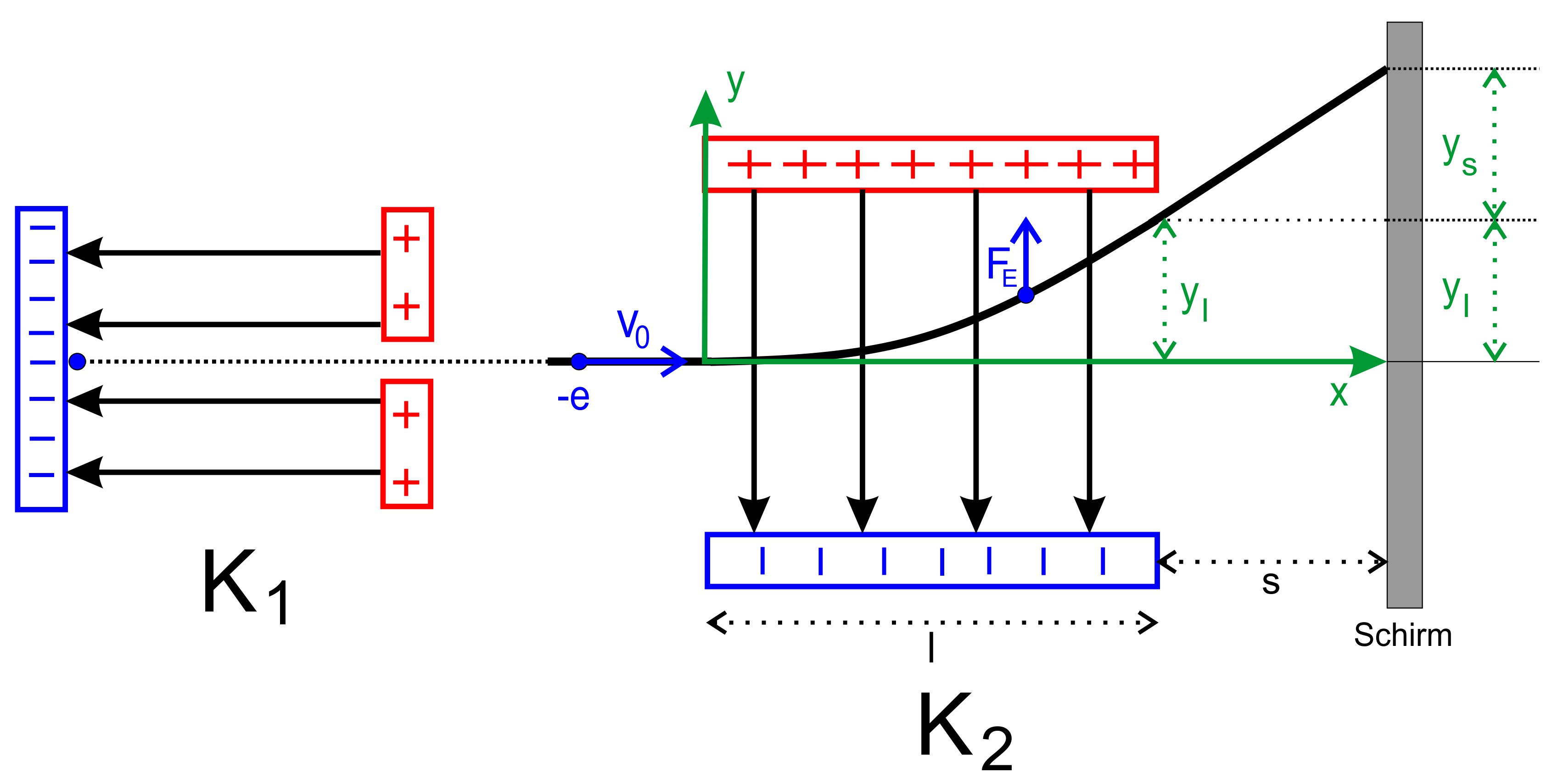
ihre Eintrittsgeschwindigkeit v₀ erreichen. Meist wird in technischen

Anwendungen die Beschleunigung auf v₀ durch einen weiteren Kon-

densator vorgenommen. Man spricht vom Beschleunigungskonden-

sator.

Es liegt also meist folgende Situation vor.

In einem Beschleunigungskondensator K₁ werden die Elektronen auf

die Geschwindigkeit v₀ beschleunigt und gelangen dann erst in den

Ablenkungskondensator K₂.

Der Kondensator K₁ habe die Spannung U₁ und der Kondensator K₂

besitzt die Spannung U₂.

Hinweis: Da die Masse der Elektronen mit m_e = 9,1094 ∙ 10⁻³¹ kg extrem gering ist, kann man

bei allen Betrachtungen F_G vernachlässigen.

Es liegt der gleiche Fall wie bei den Übungsaufgaben Nr.1 vor.

Es gilt also:

Wir haben jetzt also eine zweite Formel für die Ablenkung.

Ablenkung im Kondensator 2

mit

U₁ = Spannung am Beschleunigungskondensator

U₂ = Spannung am Ablenkungskondensator

d = Abstand der Platten

Es liegt eine deutlich einfachere Formel vor.

Für die Ablenkung am Ende des Kondensators gilt:

1. Hinweis: Hier erkennt man sofort, dass somit gilt:

d.h. die Ablenkung ist proportional zur Ablenkspannung.

2. Hinweis: Schaut man sich die Formel genauer an, erkennt man,

dass die Art der Ladung keine Rolle mehr spielt für die Ablenkung,

falls die Ladung in einem Beschleunigungskondensator beschleunigt

wurde.

Falls keine Beschleunigung durch einen Kondensator stattfindet

(z.B. radioaktive Strahlung s.dort), dann muss „e“ und „m_e“ entsprech-

end ersetzt werden durch „q“ und „m_q“.

Gesamtablenkung bis zum Schirm

Da man im Experiment bzw. in der technischen Anwendung immer

auf die Ablenkung auf dem Schirm schaut, ist es interessant auch hier

noch einmal die Gesamtablenkung zu betrachten.

Hier soll folgender Ausschnitt aus den obigen Abbildungen dienen.

Wir versuchen zunächst y_s zu bestimmen. Hierzu ist der Geschwindig-

keitsvektor beim Austritt des Elektrons aus dem Kondensator einge-

tragen. Wir betrachten jetzt das Dreieck mit den Geschwindigkeits-

komponenten und dem Winkel α. Daneben geht es um das Dreieck

aus den Strecken „s“ und „y_s“ mit ebenfalls dem Winkel α.

Für α gilt jeweils:

Für die Gesamtablenkung y_g gilt dann:

Wenn man die Beschleunigungsspannung U₁ in Spiel bringen will,

geht man folgendermaßen vor.

Dies ähnelt sehr der Formel für y_l.

Für die Gesamtablenkung am Schirm gilt dann also

Gesamtablenkung

ohne Beschleunigungs- spannung

mit Beschleunigungs- spannung

zu

- Aufbau - Bewegungsanalyse - Analyse mit Beschleunigung

- Formel für y_l (ohne Spannung) - Formel für y_l (mit Spannung)

- Gesamtablenkung (Herleitung) - Gesamtablenkung (Formel)

- Kapitel „Plattenkondensator“

- Übungsaufgaben zur Ablenkung im Kondensator

- Klausuraufgaben zur Ablenkung im Kondensator

- Anwendungen des Ablenkkondensators: Oszilloskop

- Übersicht „Felder“