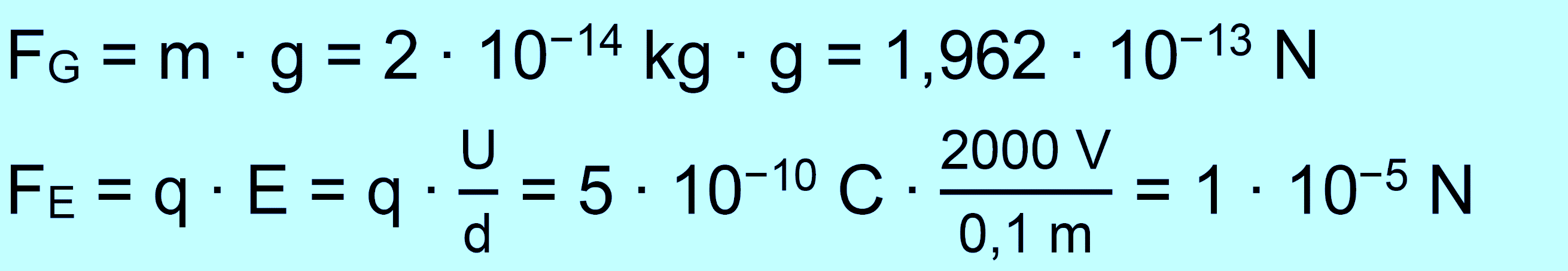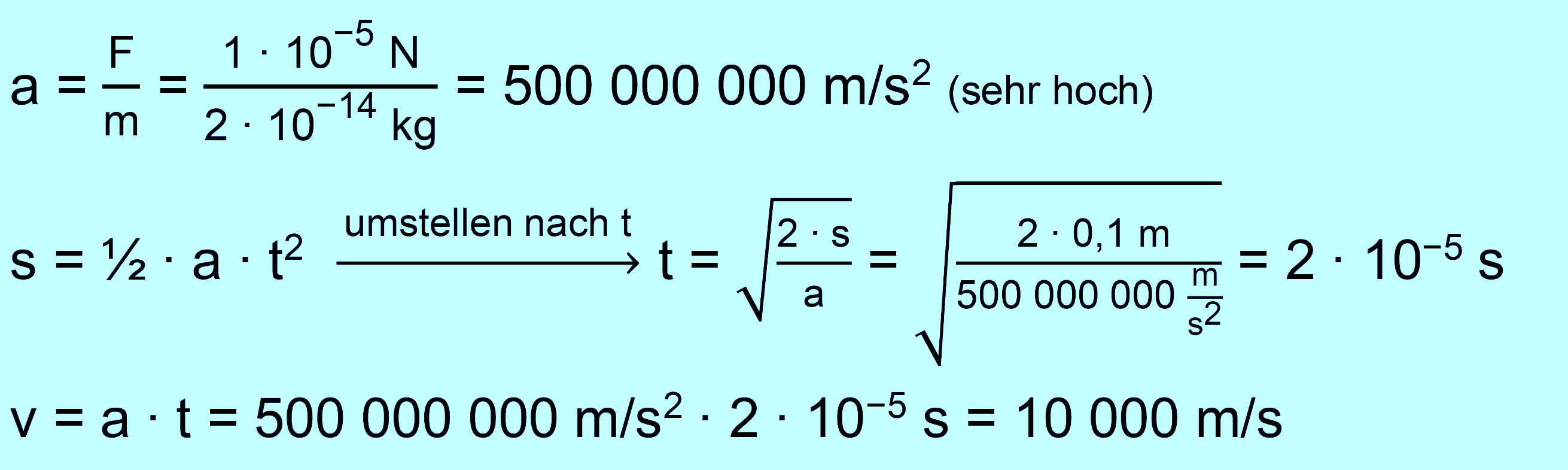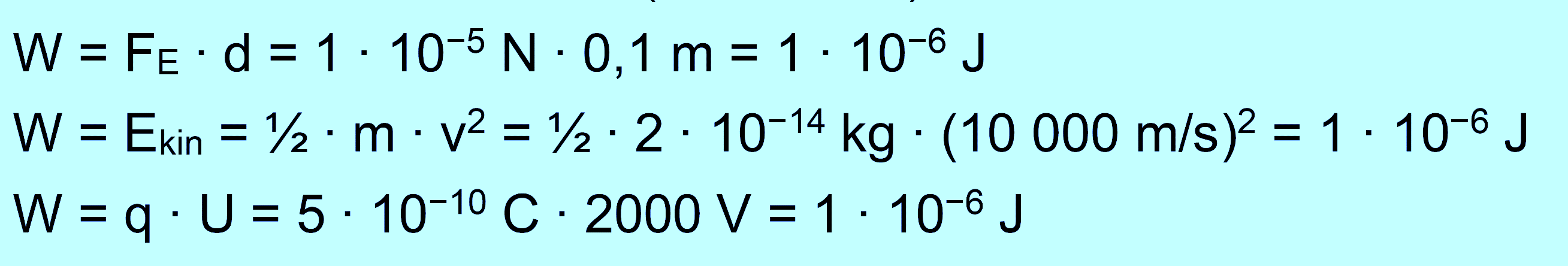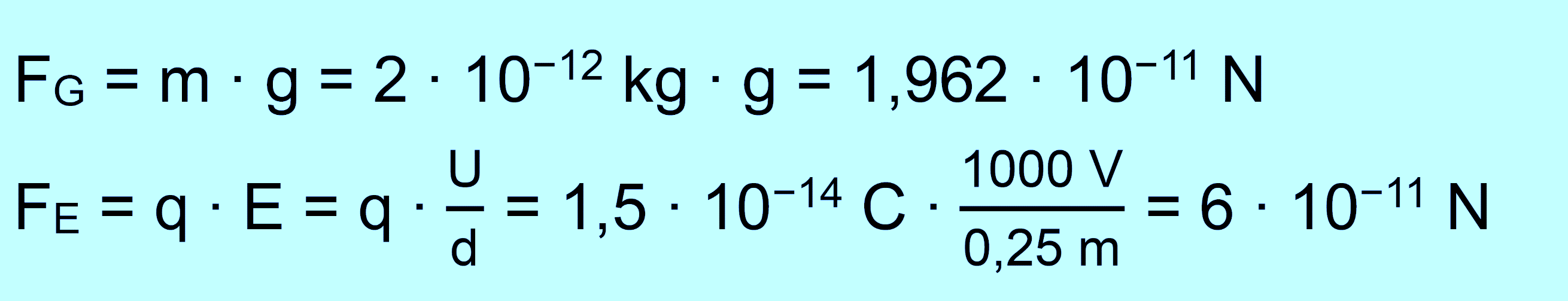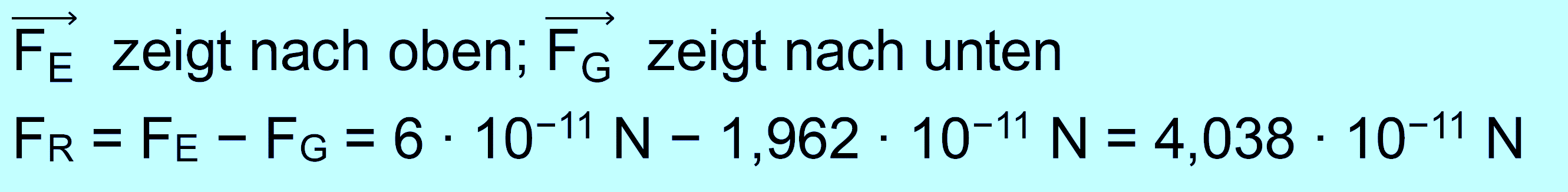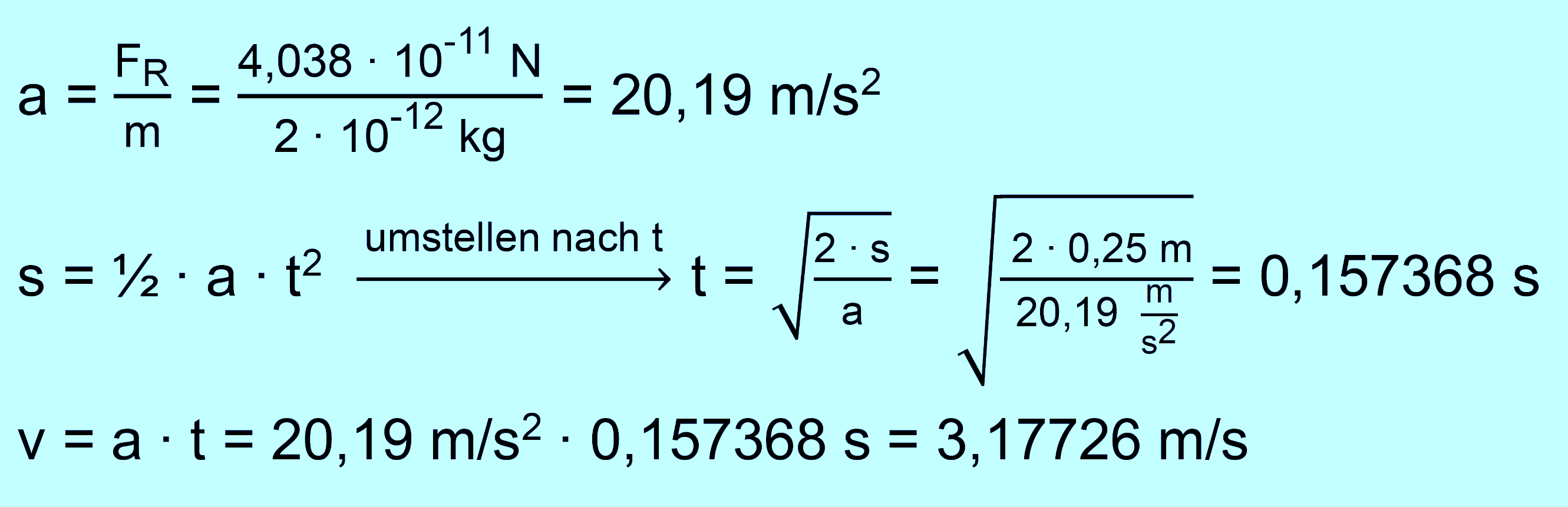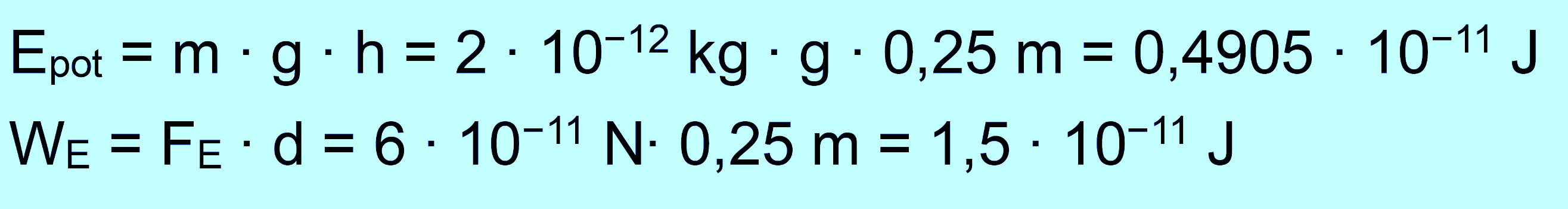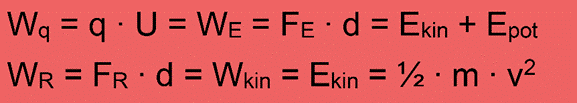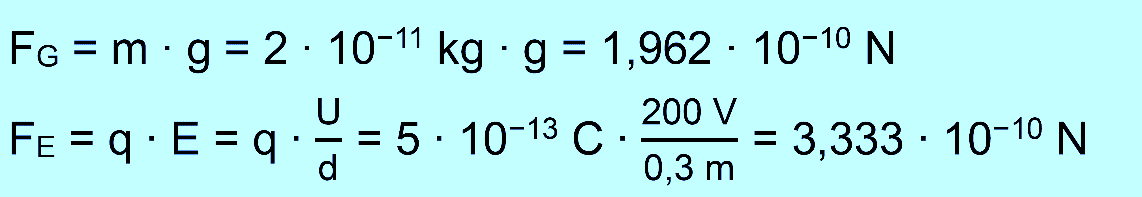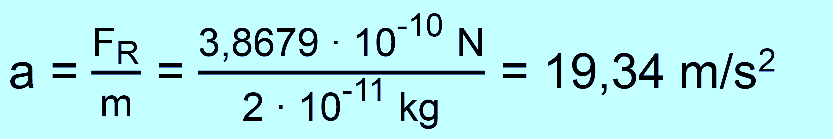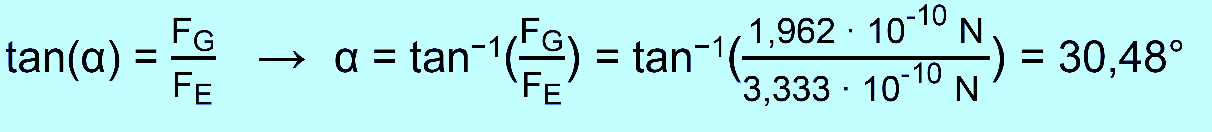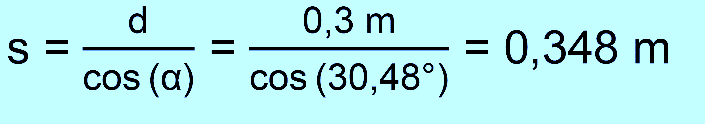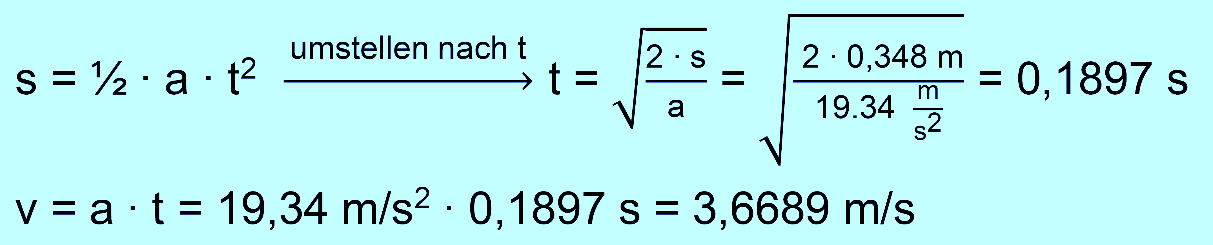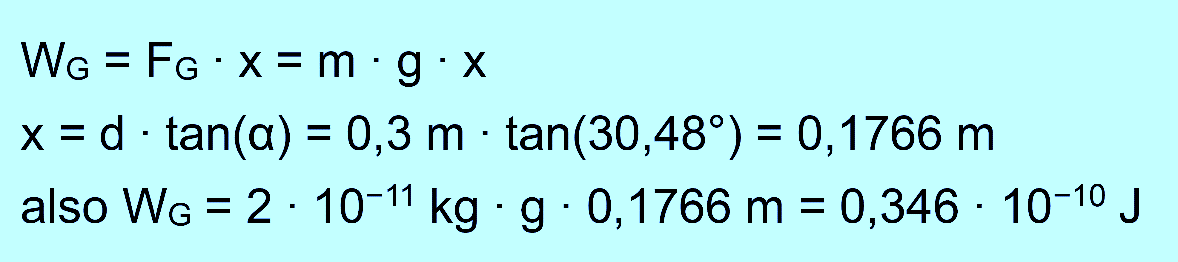|
Hinweis: Für die Lösung dieser Aufgaben müssen Sie aus der
E-Phase die Kapitel „Bewegung“ und „Arbeit und Energie“
bearbeitet haben. 1.
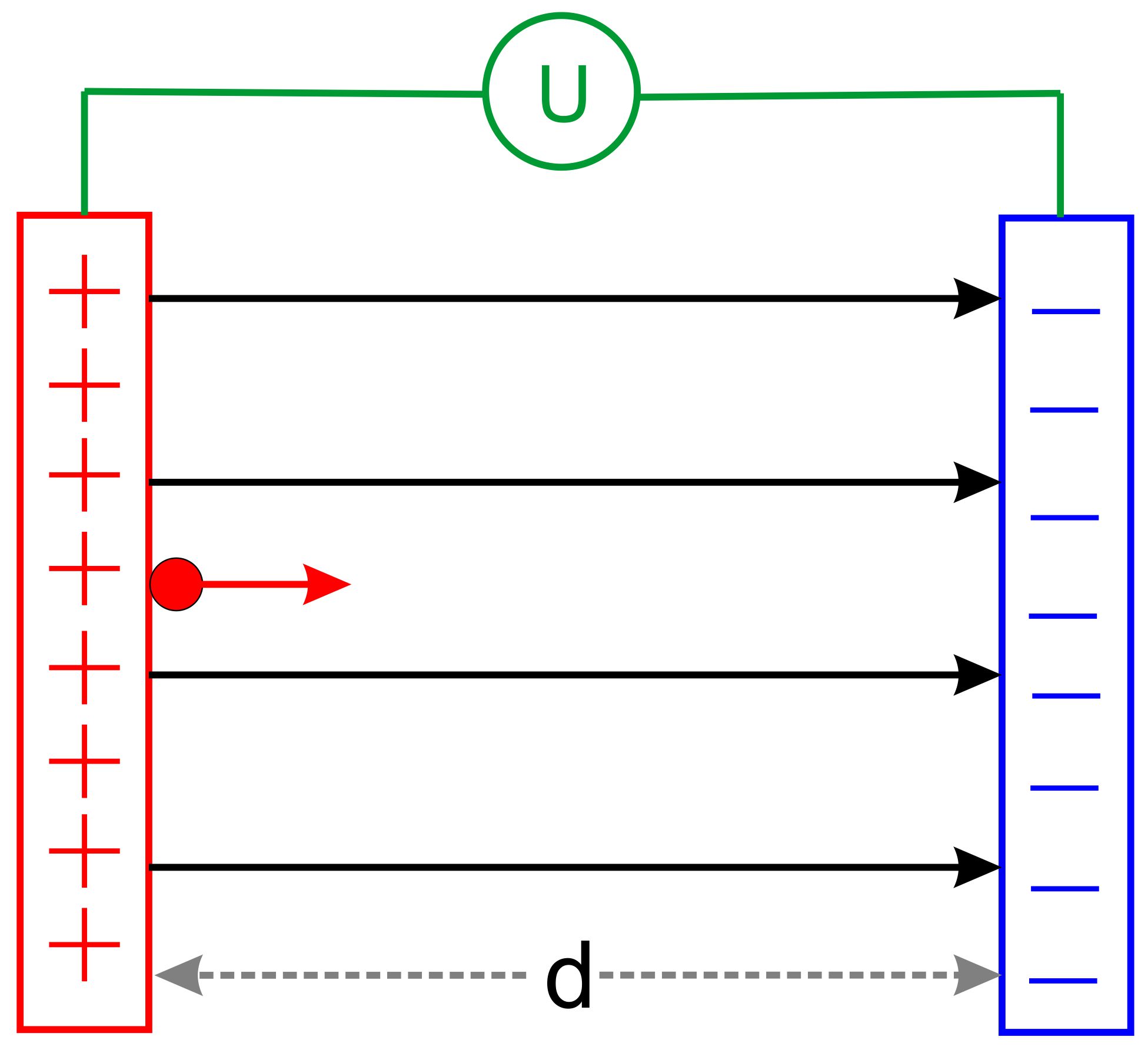
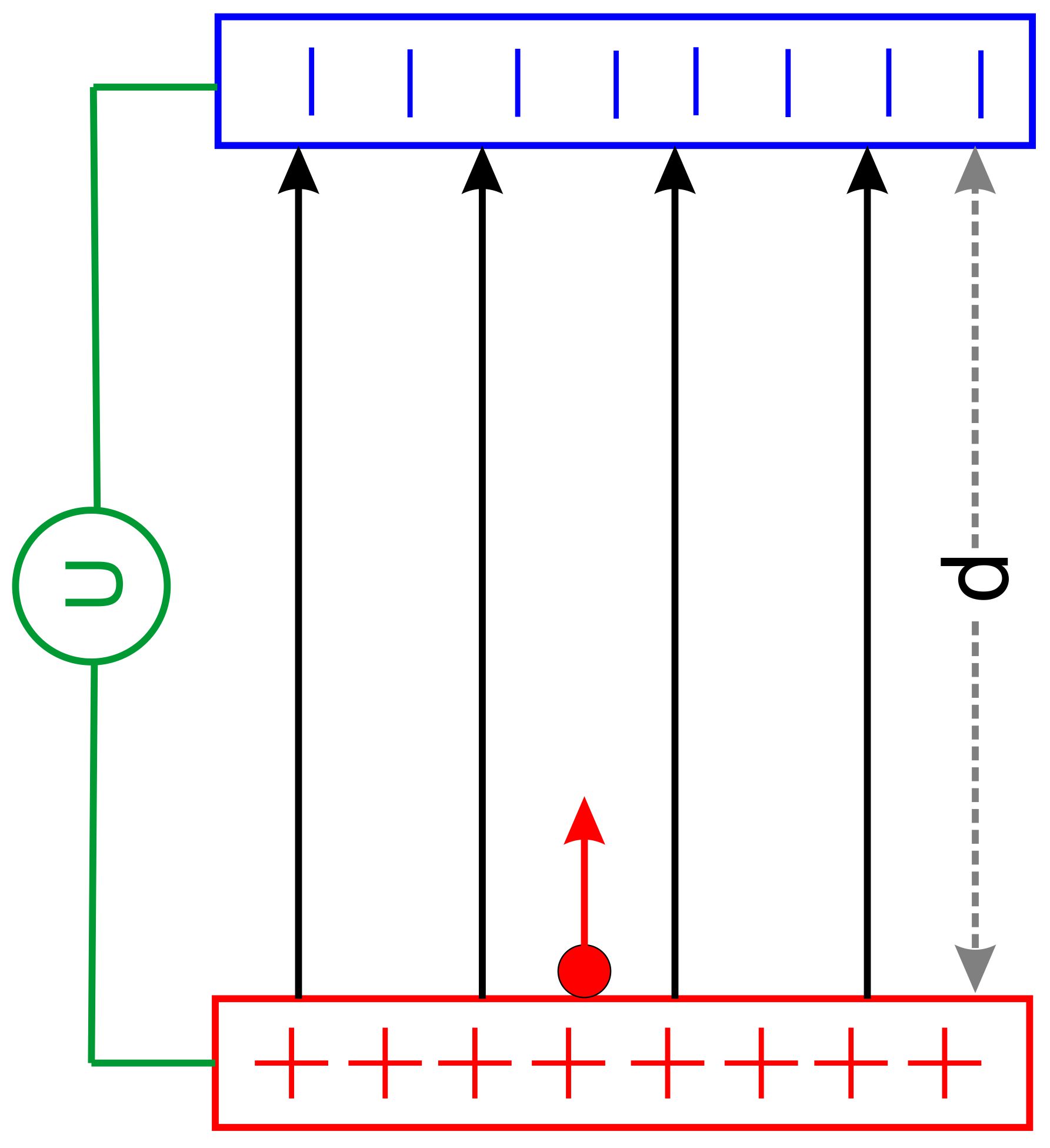
Aufgabe Ein vertikal
ausgerichteter Kondensator (s. Abb.) liegt vor. Auf der positiven
Seite taucht eine „unendlich kleine“ positive Ladung q = 5 ∙
10−10 C auf. Die Masse von q beträgt m = 2 ∙ 10−14
kg. Die an- gelegte
Spannung U beträgt 2000 V. Der Abstand der Platten d = 10 cm.
Lösung Es gibt zwei Kräfte, nämlich die
Gewichtskraft und die elektrische
Man erkennt, dass FG << FE , also betrachten wir nur FE weiter. Da das Feld homogen ist, wird q gleichmäßig beschleunigt. Man kann also die Formeln zur „gleichmäßig beschleunigten Bewegung“ benutzen. Zunächst berechnen wir mit
der „Grundgleichung
der Mechanik“ die Beschleunigung a.
Für die Berechnung der verrichteten Arbeit gibt es verschiedene Wege. Man kann mit der Arbeitsformel
rechnen oder man bestimmt die auftretende kinetische
Energie. Als drittes könnte man noch die Formel aus der Mittelstufe (Stromfluss) wählen.
2.
Aufgabe In der
folgenden Aufgabe ist der Kondensator horizontal ausgerichtet. Es gilt: U
= 1000 V, m = 2 ∙ 10−12 kg, d = 25 cm, q = 1,5 ∙
10−14 C
Lösung Zunächst die
Berechnung der Kräfte wie bei Nr.1.
In diesem Fall ist FE
in der Nähe von FG, d.h. beide Kräfte müssen Berücksichtigung
finden. Für die resultierende Kraft gilt:
Für die Bewegungsaufgaben muss FR betrachtet werden.
Wir rechnen für die
Arbeiten und Energien zunächst einmal wie bei Nr.1
Irgendwie passt es
jetzt nicht, weil Wq ≠ WR
= Wkin Wo ist das Problem?
Wir haben die potentielle Energie nicht berücksichtigt, da ja
jetzt auch das Gravitationsfeld eine Rolle spielt. Berechnen wir jetzt
noch zusätzlich die gewonnene potentielle Ener- gie.
Außerdem bestimmen wir noch die allein vom elektrischen Feld verrichtete Arbeit.
Es gilt also:
Wir halten fest: Die vom elektrischen Feld verrichtete Arbeit kann man auf zwei verschiedene Arten bestimmen, nämlich mit WE = q ∙ U
= FE ∙ d Diese verrichtete Arbeit führt zu verschiedenen Energien bei q. Wenn es nur um die Bewegung geht, gilt WR = FR
∙ d = Ekin = ½ ∙ m ∙ v2 3. Aufgabe Die
Lage des Kondensators ist wie in Nr.1, also vertikal. Es
gilt: U = 200 V, d = 30 cm, q = 5 ∙ 10−13 C, m = 2 ∙
10−11 kg Die
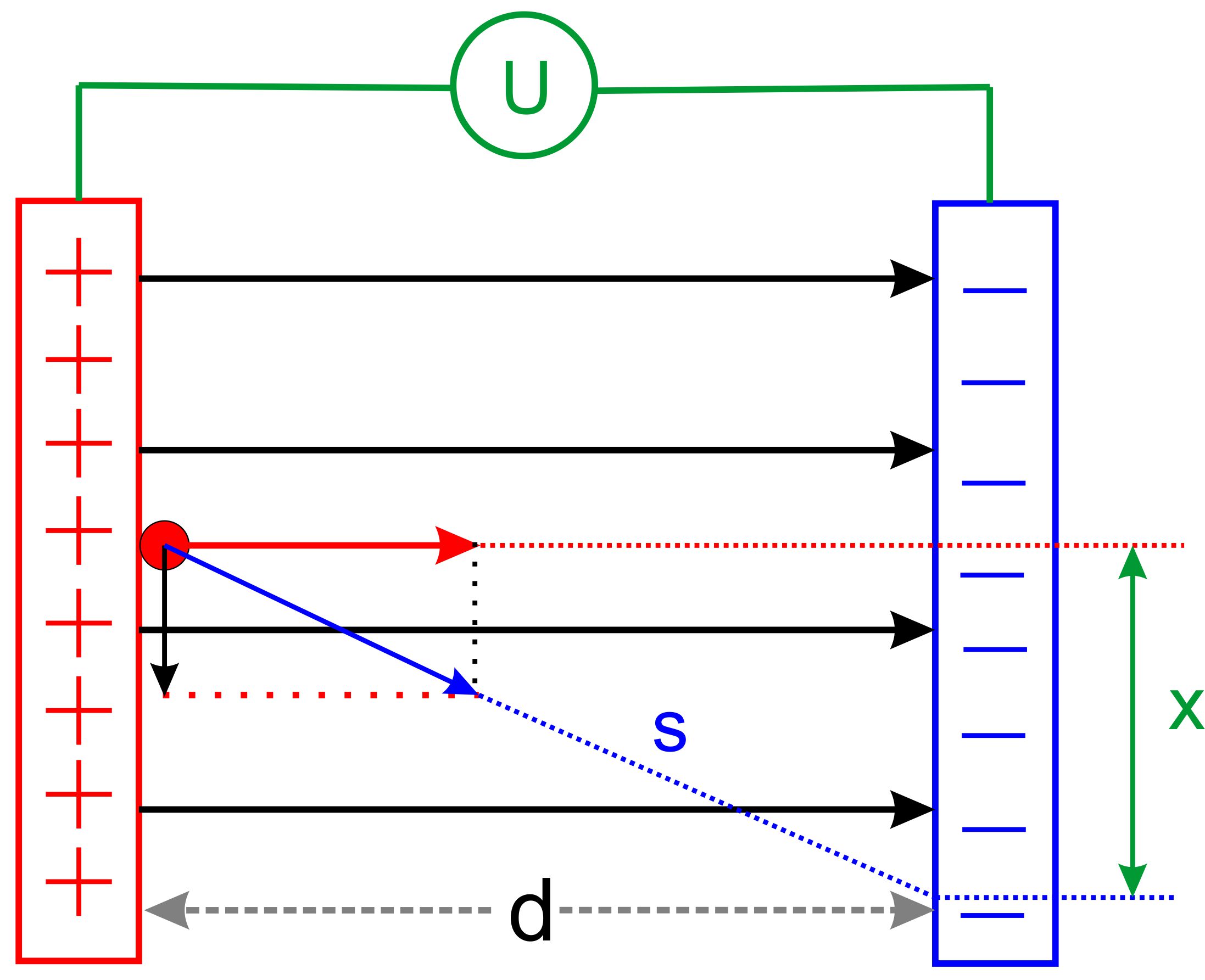
schon bekannten Fragen aus 1.) bzw. 2.) sollen beantwortet werden. Hierzu soll die folgende Abbildung behilflich sein.
Lösung Berechnung der Kräfte wie gehabt.
Die Kräfte haben
ähnliche Größen, also müssen beide berück- sichtigt
werden. Aber jetzt stehen die Kräfte senkrecht zueinander. FE
zeigt senkrecht zu den Platten FG zeigt zum Erdmittelpunkt FR ist die resultierende Kraft, die sich durch
Vektoraddition ergibt.
Die Beschleunigung gewinnen wir wieder
über die Grundgleichung
s ist leider nicht d,
sondern die gestrichelte blaue Linie. Wir müs- sen
s zunächst bestimmen. Dazu wäre es nützlich, wenn man den Winkel α
zwischen FE und FR kennen würde. Es gilt:
also
jetzt die Rechnung
wie bisher
Nun die Rechnung zu den
Arbeiten und Energien (wie bisher).
Die Werte passen
zunächst einmal zu den Gleichungen von Nr.2. Wir haben allerdings
eine größere Energie als wir an Arbeit ver- richtet haben. Dies
widerspricht völlig dem Energieerhaltungssatz. Wir hätten ein
„perpetuum mobile“. Wir haben vergessen, dass neben dem
elektrischen Feld auch das Gravitationsfeld Arbeit ver- richtet hat. Die
Ladung hat ja an Höhe und somit an potentieller Energie verloren.
Jetzt passt es.
- zu Aufgabe 1 - zu Aufgabe 2 - zu Aufgabe 3 |