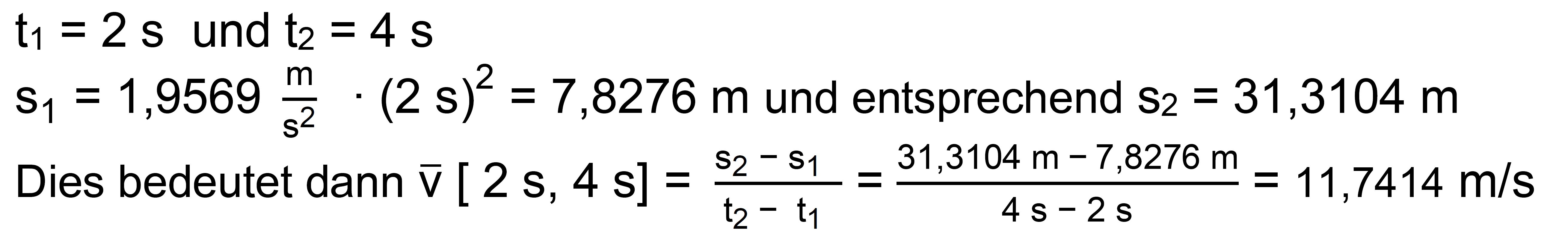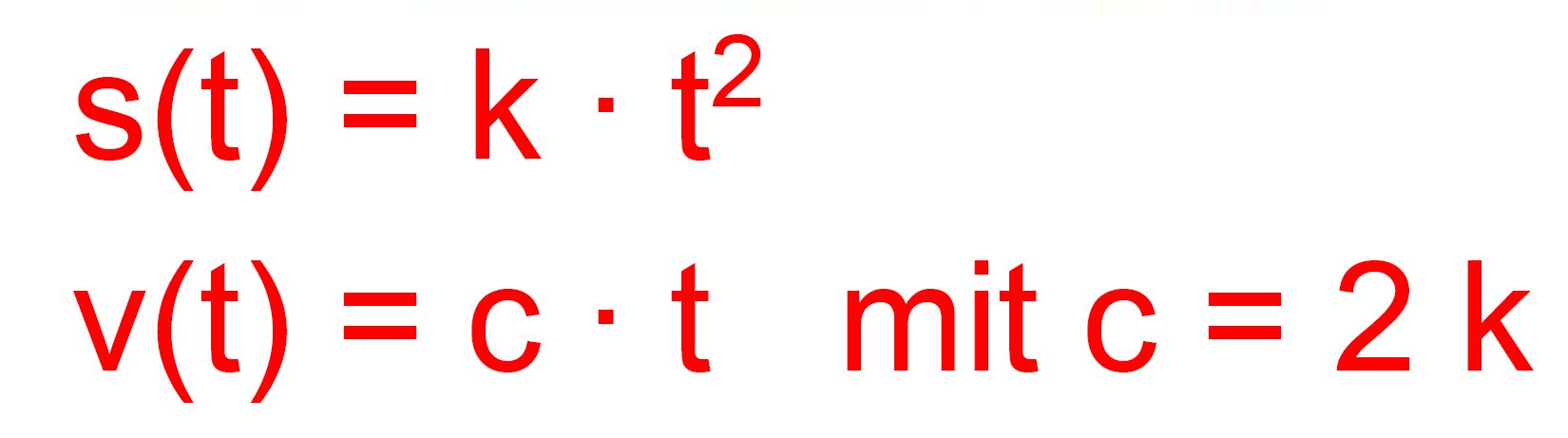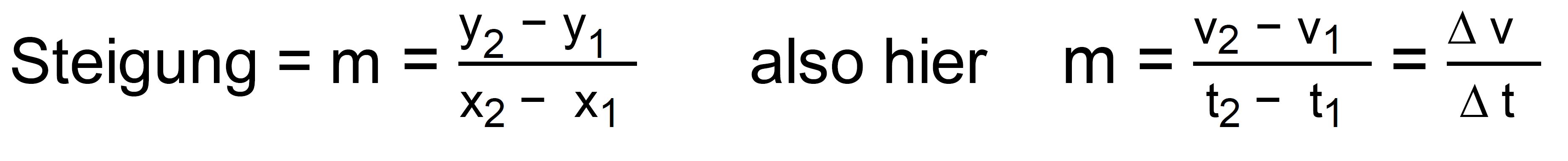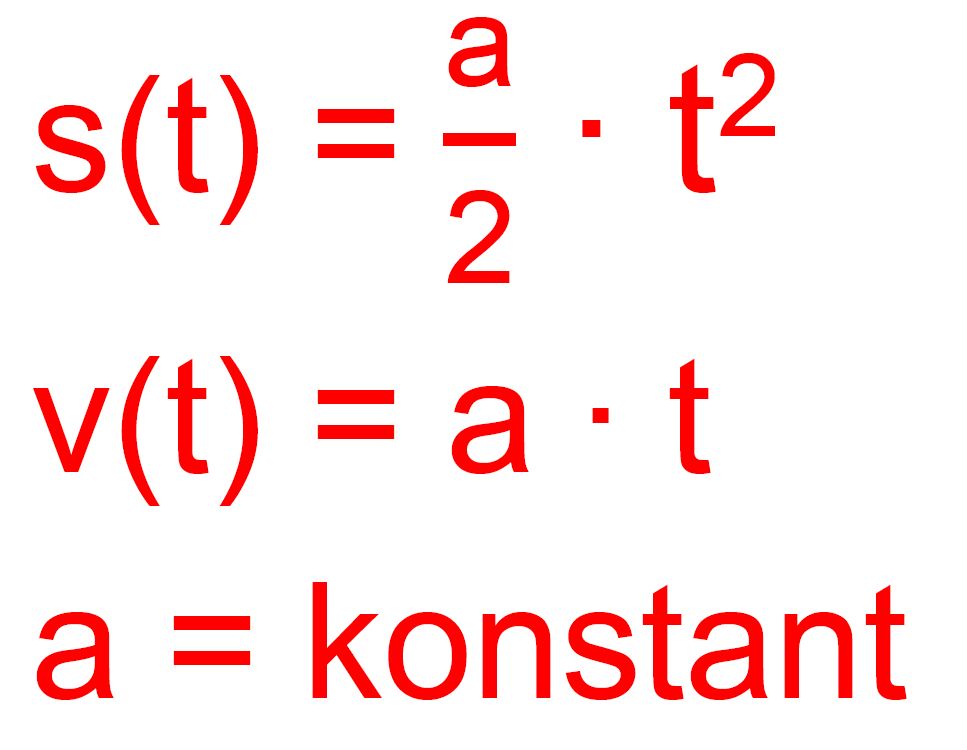|
Untersuchung
einfacher Bewegungen Gleichmäßig
beschleunigte (geradlinige) Bewegung Unter
einer gleichmäßig beschleunigten Bewegung versteht man eine Bewegung
mit konstanter Beschleunigung. Wann liegt überhaupt eine beschleunigte
Bewegung vor? In der Physik spricht man immer dann von
einer Beschleunigung, wenn sich die Geschwindigkeit im Laufe der
Zeit ändert. Es liegt eine positive Beschleunigung vor, wenn es zu einer
Geschwindigkeitszunahme kommt. Falls die Geschwindigkeit ab- nimmt,
liegt eine negative Beschleunigung vor. Hieraus
ergibt sich sehr schnell eine Formel zur Bestimmung der Durchschnittsbeschleunigung,
nämlich
Es
ergibt sich somit die Einheit:
Wir
wollen jetzt das folgende Video mit Hilfe der Videoanalyse unter- suchen. Das
Video muss auf dem eigenen Rechner gespeichert werden.Um eine
Analyse vorzunehmen, braucht man ein Videoanalyseprogramm. In
folgendem Link wird VIMPS zum Download zur Verfügung gestellt. Das
Programm muss noch extrahiert werden. DOWNLOAD Zur
Messung mittels der Videoanalyse gibt es ein eigenes Kapitel: Videoanalyse (LINK) Nach
der Erfassung der Messwerte mittels Videoanalyse werden die Werte mittels
einer Tabellenkalkulation ausgewertet. Nach
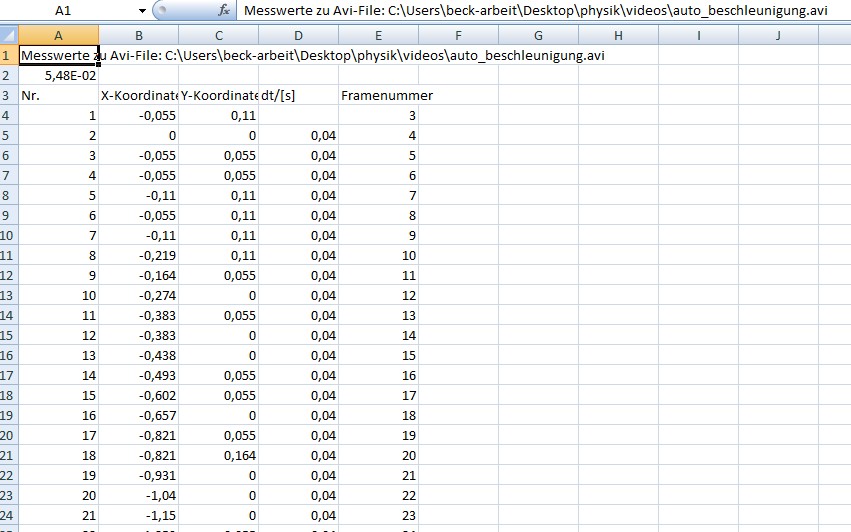
Erfassung der Messwerte ergibt sich folgende Exceldatei, wenn man
das Videoanalyseprogramm VIMPS benutzt:
Da
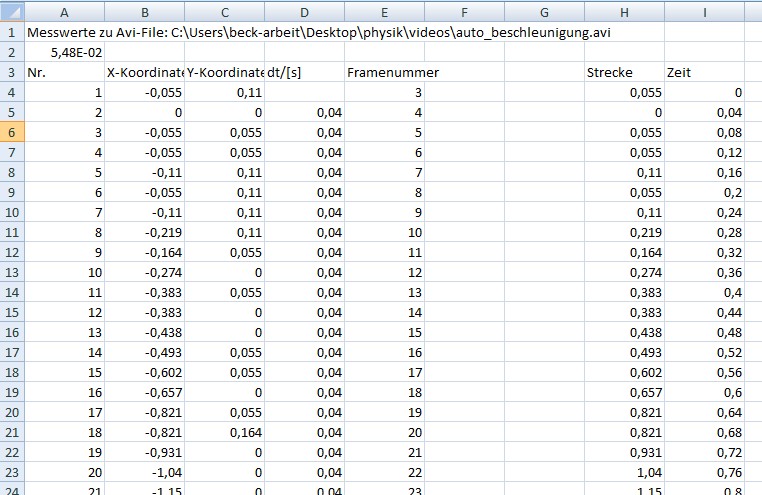
uns nur die x-Koordinate interessiert, erzeugen wir jetzt zunächst eine
Spalte, die den Strecken entspricht (Hinweis: das Minuszeichen ergibt sich durch die Nullpunktwahl). Außerdem wird aus dem Zeitabstand von 0,04
s die zugehörige Zeit berechnet.
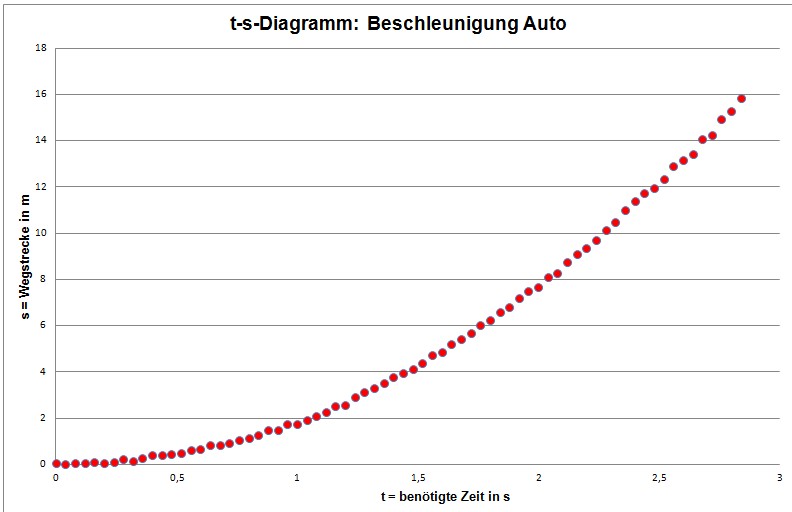
Aus
den Werten Strecke und Zeit lässt sich in Excel sehr schnell ein t-s-Diagramm
gewinnen:
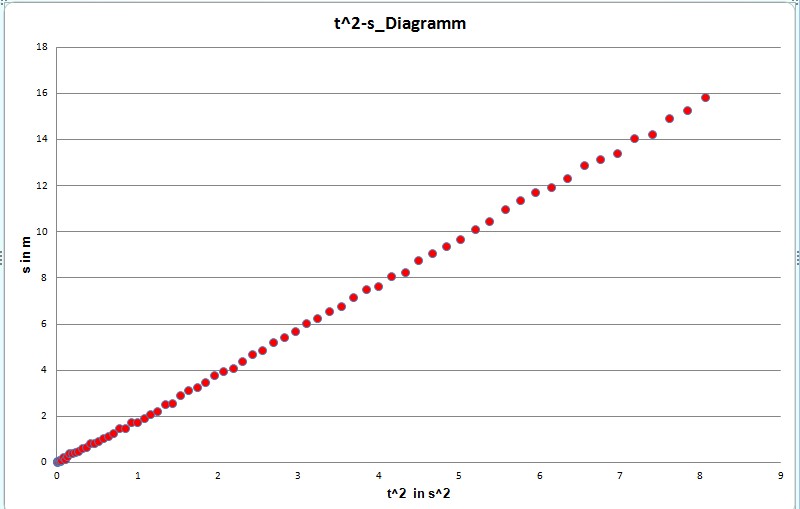
Da
sich im t-s-Diagramm offensichtlich als Trendlinie ("Realwerte ohne Messfehler")
keine Gerade ergibt, kann keine gleichförmige Bewegung vorliegen.
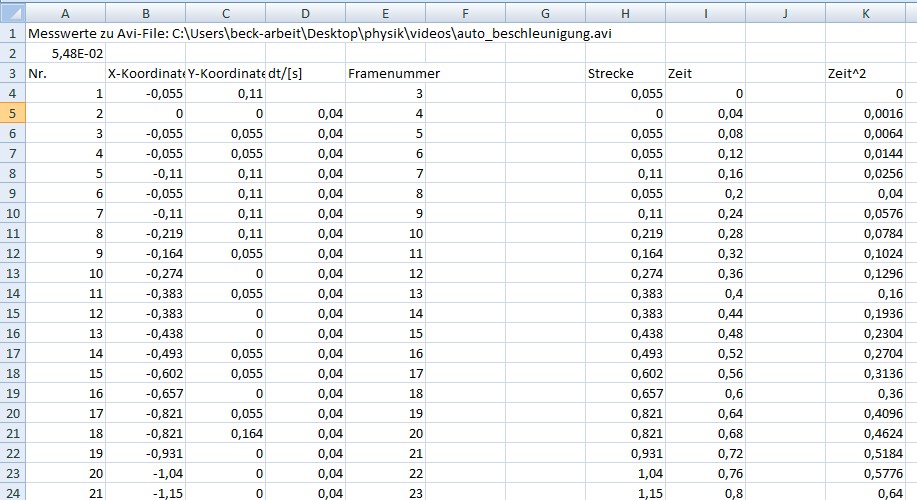
Wir untersuchen weiter, indem wir ein t2-s−Diagramm auf- stellen
Wir müssen also jetzt eine "Zeit zum Quadrat"-Spalte in Excel erstellen:
Das
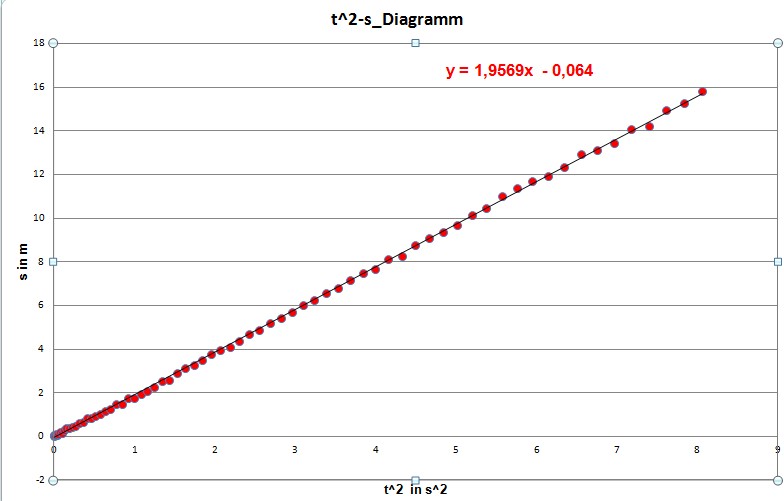
t2-s−Diagramm hat dann folgendes Aussehen:
Offensichtlich
liegt jetzt ein linearer Zusammenhang vor, so dass man als
Trendlinie die Gerade eintragen lassen kann. Man erhält dann folgendes
Bild, wobei auch schon die Formel für die Trendlinie ange- geben
ist. Es liegt eigentlich, wie man schnell überlegen kann, eine Ursprungsgerade
vor, die Excel wegen der Messfehler allerdings nur angenähert erhält.
Mathematisch
bedeutet dies, dass zwischen t und s folgende Gleich- ung gilt:
Es
liegt also ein quadratischer Zusammenhang vor, wobei k der Steigung
der Geraden entspricht. In obigen Fall hat k also den Wert k =
1,9569. Da auf der Abszisse t2 und auf der Ordinate s aufgetragen ist,
ergibt sich für die Steigung (also für k) die Einheit m/s2. Es
gilt somit
für k der Wert k = 1,9569 m/s2. Somit
erhalten wir im konkreten Fall des beschleunigenden Autos
Zeit-Geschwindigkeits-Diagramm Wie gewinnt man jetzt aus der Bewegungsgleichung, die die
Abhängig- keit zwischen Zeit und Weg angibt, eine Beziehung zwischen Zeit und Geschwindigkeit, also ein t-v−Diagramm? Nun ist es zunächst
mal kein Problem aus der t-s−Beziehung
Durchschnittsgeschwindigkeiten zu bestimmen (s.gleichförmige Bewegung). Zum Beispiel: Wollen wir die Durchschnittsgeschwindigkeit im
Zeit- raum zwischen 2 s und 4 s bestimmen, müssen wir nur die Weg- strecke für t = 2 s und die Wegstrecke für t = 4 s mit Hilfe
unserer Formel
bestimmen.
Es gilt dann also:
Wählen
wir jetzt das Intervall extrem klein, z. Bsp. nur 0,000001 s, dann
lässt sich ebenfalls das obige Verfahren anwenden, da man ja mit
Hilfe der Formel die Wegstrecken bestimmen kann. Bei sehr kleinen
Zeitintervallen entspricht aber die Durchschnittsgeschwindig- keit
praktisch der Momentangeschwindigkeit, so dass wir somit eine Möglichkeit
haben, zu jedem Zeitpunkt Momentangeschwindigkeiten zu
bestimmen, wenn wir nur das Zeitintervall extrem klein wählen. Wir
führen zunächst wieder ein Beispiel durch. Gesucht ist für die obige
Bewegung die Momentangeschwindigkeit zum Zeitpunkt t = 4 s. Man
wählt jetzt einen zweiten Zeitpunkt, der sehr nahe an t = 4 s liegt, z.
B. t = 4,000001 s. Jetzt wird die Durchschnittsgeschwindigkeit be- stimmt,
die dann der Momentangeschwindigkeit entspricht. Die Berech- nung
sieht dann folgendermaßen aus:
Dies
kann man jetzt für jeden beliebigen anderen Zeitpunkt durch- führen
und erhält dann ein t-v−Diagramm. Am schnellsten gehen die Berechnungen
mit Excel. [Hinweis:
Mit etwas Mathematik kann man die Gleichung für die
Momentangeschwindigkeit auch direkt gewinnen. In
der Mathematik geht es hier um die Ableitung von s(t) nach t. Die
Durchschnittsgeschwindigkeit entspricht dort
dem Differenzenquotienten. Es gilt dann: v(t) = s'(t)] Es
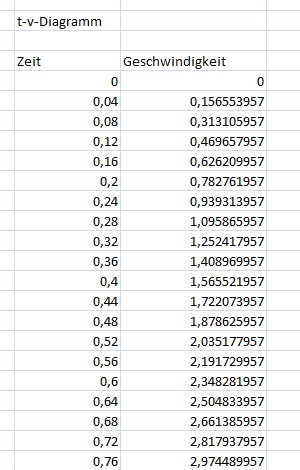
ergeben sich folgende Excel-Tabellen und Diagramme:
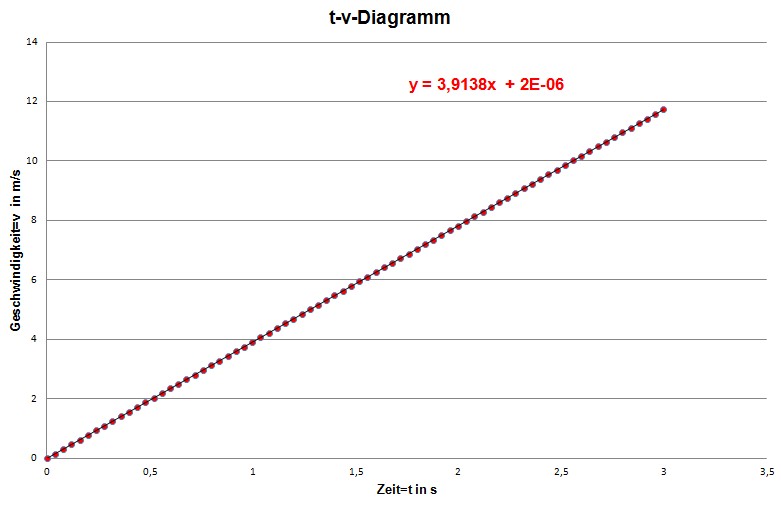
Man
erkennt sofort, dass ein linearer Zusammenhang (Ursprungs- gerade)
zwischen Zeit und Geschwindigkeit besteht. Die Funktions- gleichung
lautet also v = c ∙ t, wobei c die Steigung der Geraden be- deutet.
Man erkennt auch, dass die Steigung der t-v-Gerade doppelt so
groß ist wie bei der t2-s−Gerade. Es gilt also: c = 2 k. Konkret
also v = 3,9138 m/s2 ∙ t. Die Einheit ergibt sich aus den
Ein- heiten
der Geschwindigkeit m/s durch die Einheit der Zeit s. Wir
fassen zusammen:
Welche
Bedeutung hat im t-v-Diagramm die Steigung der Geraden? Falls man die
Steigung mittels Steigungsdreieck bestimmen möchte, müsste man folgende
Formel benutzen:
Dies
entspricht der Durchschnittsbeschleunigung (s. oben). Da eine Gerade
vorliegt, liegt in jedem Zeitintervall dieselbe Durchschnitts- beschleunigung
vor, damit entspricht diese der Momentanbe- schleunigung.
Für die Bewegung des grauen Autos gilt also:
Der
PKW führt also eine Bewegung mit konstanter Beschleunigung durch.
Man spricht von einer gleichmäßig beschleunigten Bewegung. Da
c = a = 2 k ist, gilt also insgesamt für eine gleichmäßig beschleunig- te Bewegung:
Diese
Bewegungsgleichungen gelten, wenn die Streckenmessung s mit
t = 0 s beginnt. Falls bei t = 0 s schon eine Strecke s0 zurückgelegt hat
und/oder sich schon bei t = 0 s mit der Geschwindigkeit v0
bewegt, gilt:
|