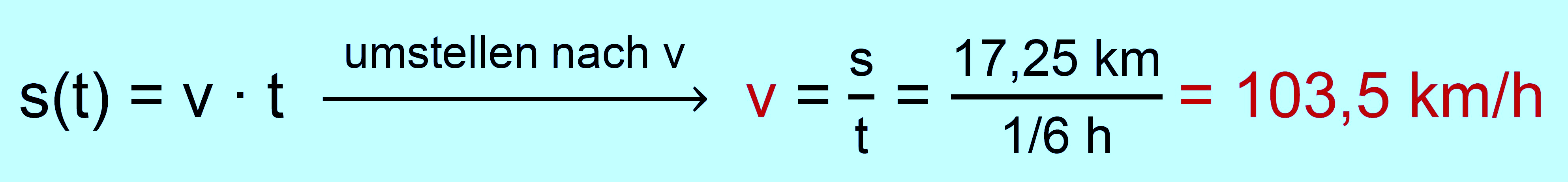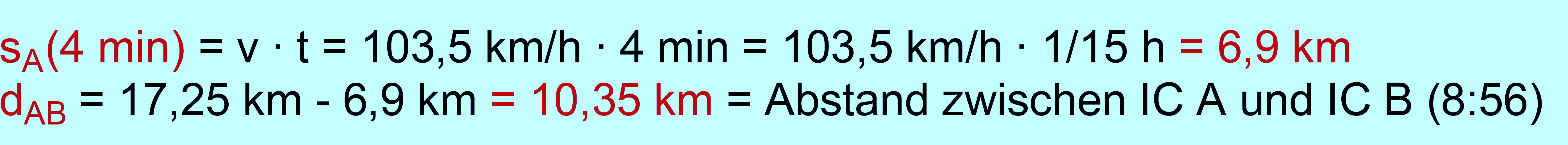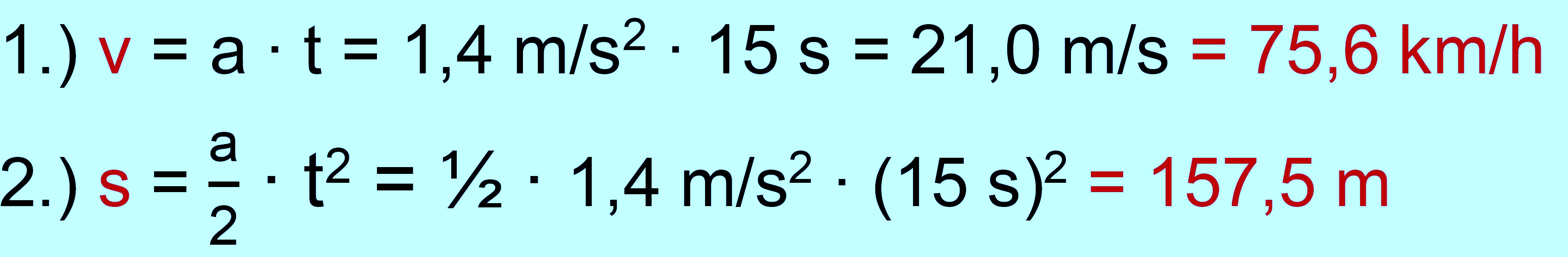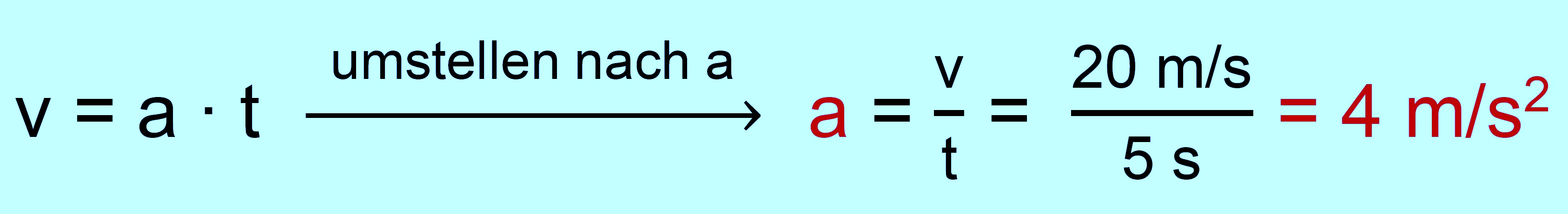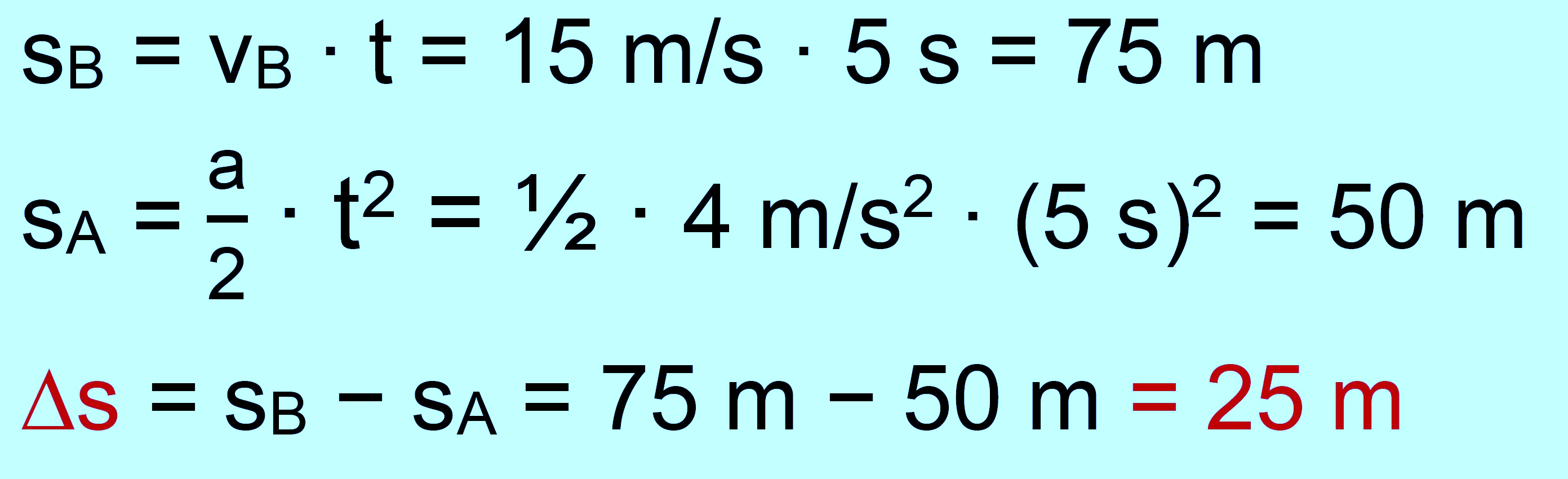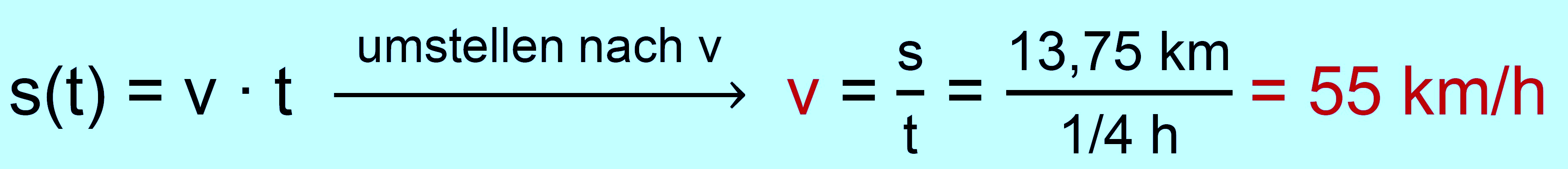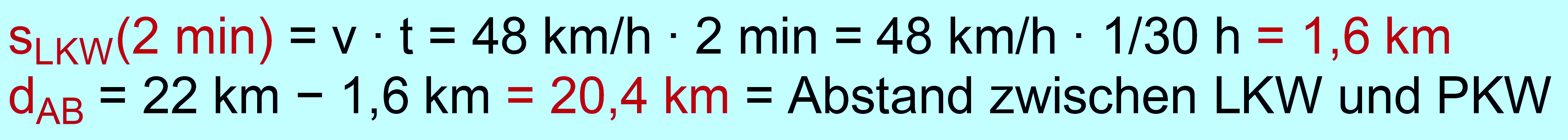|
zur Hinweis: Es werden Kenntnisse aus den
Kapiteln „Einfache Bewegung (gleich- förmig) und „Gleichmäßig beschleunigte Bewegung“
benötigt
Einfache Bewegungen 1. Klausuraufgabe − IC Aufgabe (einfach-mittel-schwer) a.) Der Intercity IC A von Bielefeld nach Hamm
passiert um 8:52 Uhr den Bahnhof Brackwede und um 9:02 Uhr den
Hauptbahnhof Gütersloh. Die Entfernung zwischen beiden Bahnhöfen beträgt
17,25 km. In der Gegenrichtung fährt der IC B von Hamm nach
Bielefeld. Dieser durchfährt die 7,5 km lange Strecke zwischen
Rheda und Gütersloh mit der Geschwindigkeit 125 km/h. Die Bewegung der
ICs soll gleichförmig sein. a.1.) Berechnen Sie die Geschwindigkeit (in km/h)
von IC A. [ Zur Kontrolle: v =103,5 km/h]
(einfach) a.2.) Bestimmen Sie die Zeit (in Minuten), die
der IC B für die Strecke zwischen Rheda und Gütersloh braucht. (einfach) a.3.) Untersuchen Sie, nach welcher Zeit (in
Minuten) sich die beiden Züge treffen, wenn der IC B um 8:56 Uhr Gütersloh
passiert. (Zeit: Fahrtzeit IC B ab Gütersloh ) (mittel-schwer) b.) Der IC C startet in Bielefeld um 10:00 Uhr
mit der gleichmäßigen Beschleunigung von a = 1,4 m/s2. Die Beschleunigung dauert 15 s. b.1.) Berechnen Sie die Geschwindigkeit in km/h
des IC C nach 15 s.
(einfach) b.2.) Bestimmen Sie die Strecke, die der IC C in
dieser Zeit zurück- gelegt hat. (einfach) c.) Der IC D beginnt um 10:10 Uhr bei einer
Geschwindigkeit von 100 km/h mit dem Bremsvorgang in Gütersloh. Der
Bremsweg beträgt 300 m. Der Bremsvorgang soll gleichmäßig
beschleunigt sein. Berechnen Sie die Dauer des Bremsvorgangs und die Verzögerung. Lösung: zu a.1.) gegeben: s = 17,25 km; t = 10 min = 1/6 h;
gleichförmig gesucht: v
zu a.2.) gegeben: s = 7,5 km; v = 125 km/h;
gleichförmig gesucht: t in min
zu a.3.) wenn der IC B um 8:56 Uhr Gütersloh
passiert, hat der IC A schon eine gewisse Strecke ab Brackwede
zurückgelegt. Man muss also zunächst die Strecke bestimmen, die der IC A
in 4 min zurücklegt. Dann weiß man, wie groß der Abstand zwischen
den Zügen um 8:56 Uhr ist.
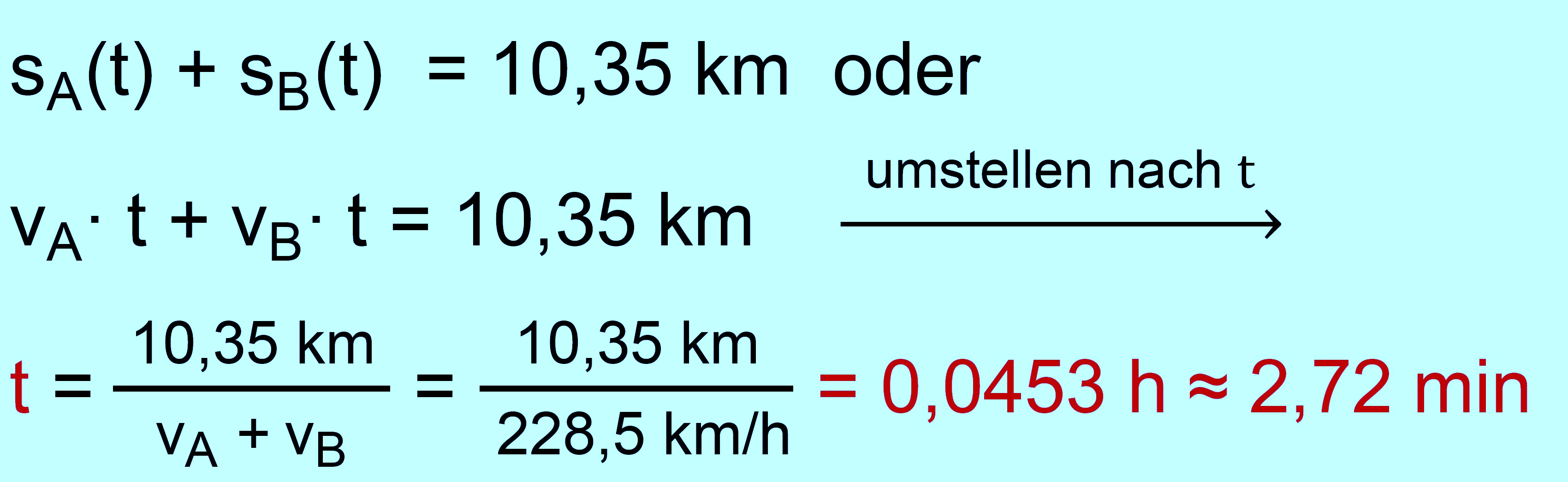
Wenn die Züge sich nach der Zeit t
treffen, gilt:
zu b.) gegeben: a = 2,5 m/s2; t
= 15 s, gleichmäßig beschleunigt gesucht: v in km/h, s
zu c.) gegeben: s = 300 m; v = 100 km/h;
gleichmäßig beschleunigt gesucht: t Es gibt als Standardformel nur: I.)
s
= ½ ∙
a ∙ t2
und II.) v = a ∙ t In beiden Formeln wird zur Berechnung „a“ benötigt.
„a“ ist aber nicht angegeben. Man muss also eine neue Formel
aufstellen, in der „a“ fehlt und nur die gegebenen Größen vorkommen. Hierzu kann
man eine Formel nach „a“ auflösen und diese dann in die
andere Formel ein- setzen.
Extra: Links zur
Klausuraufgabe Nr.1
2. Klausuraufgabe − PKW Aufgabe (einfach-mittel) Ein Auto A startet bei Grün an einer Ampel und erreicht
nach 5 s bei gleichmäßig beschleunigter Bewegung die Geschwindigkeit vA= 72 km/h. a.) Berechnen Sie die Beschleunigung von A.
[Zur Kontrolle: a = 4 m/s2] (einfach) b.) A beschleunigt 10 Sekunden lang. Bestimmen Sie die Geschwindig- keit (in km/h), die A dann aufweist.(einfach) Im Moment des Startes (t = 0 s) wird A von einem PKW B
mit der kon- stanten Geschwindigkeit 54 km/h überholt. c.) Untersuchen Sie, wie lange es dauert, bis A so
schnell fährt wie B? (einfach) d.) Berechnen Sie den Vorsprung von B nach 5 Sekunden?
(einfach) e.) Bestimmen Sie den Zeitpunkt für A, zu dem A das Auto
B einholt. Berechnen Sie auch die Entfernung von der Ampel, die dann
vorliegt. Lösung: zu a.) gegeben: v = 72 km/h = 20 m/s; t = 5 s; gleichmäßig beschleunigt gesucht: a
zu b.) gegeben: t = 10 s; a = 4 m/s2;
gleichmäßig beschleunigt gesucht: v in km/h
zu c.) gegeben:
v = 54 km/h = 15 m/s; a = 4 m/s2; gleichmäßig beschleunigt gesucht: t
zu d.) gegeben: vB
= 15 m/s gleichförmig; a = 4 m/s2;
t = 5 s gesucht: ∆s = Abstand
zu e.) gegeben: a = 4 m/s2; vB = 15 m/s gesucht: t, s „Einholen“ bedeutet, dass beide PKW
in Bezug auf die Ampel die gleiche Strecke zurückgelegt haben.
3. Klausuraufgabe − PKW+LKW Aufgabe
(einfach-mittel-schwer) a.) Ein LKW fährt
mit der Geschwindigkeit v = 48 km/h von A nach B. Zwei Minuten nachdem der LKW in A gestartet ist, beginnt
ein PKW seine Fahrt von B nach A. 15 Minuten nach seinem Start
bei B hat der PKW eine Strecke von 13,75 km zurückgelegt. Hinweis: Die Bewegungen sollen
gleichförmig sein. 1.) Nach
welcher Fahrtzeit (Minuten) kommt der LKW in B an? (einfach) Die Fahrtstrecke von A nach B
beträgt 22 km. 2.) Welche
Geschwindigkeit (km/h) weist der PKW auf ? [ zur
Kontrolle: vPKW = 55 km/h ] (einfach) 3.) Nach
welcher Zeit trifft der PKW-Fahrer den LKW-Fahrer? (Zeit =
Fahrtzeit des PKWs in Minuten)(mittel-schwer) b.) Ein LKW
beschleunigt aus dem Stand 3,5 Sekunden lang gleich- mäßig mit der Beschleunigung 2,15 m/s2. Welche
Geschwindigkeit (m/s) weist der Wagen nach der Beschleunigungsphase auf?
(einfach) c.) Ein PKW
beschleunigt aus dem Stand auf einer Strecke von 80 m gleichmäßig. Er fährt am Schluss mit einer
Geschwindigkeit von 22 m/s. Mit welcher Beschleunigung wurde der PKW gefahren? Welche Zeit brauchte der PKW für
die Strecke? (mittel-schwer) Lösung: zu a.1.) gegeben: v = 48 km/h; s = 22 km;
gleichförmig gesucht: t
zu a.2.) gegeben: s = 13,75 km; t = 15 min =
900 s = 0,25 h, gleichförmig gesucht: v
zu a.3.) gegeben: vLKW
= 48 km/h; vPKW = 55 km/h; gleichförmig gesucht: t bis zum Treffen Wenn der PKW in B startet, hat der LKW schon eine gewisse
Strecke zurückgelegt. Man muss also zunächst die Strecke
bestimmen, die der LKW in 2 min zurücklegt. Dann weiß man, wie groß der
Abstand zwischen LKW und PKW ist, wenn der PKW startet.
Wenn die Fahrzeuge sich nach der Zeit t treffen, gilt:
zu b.) gegeben: a = 2,15 m/s2; t = 3,5 s; gleichmäßig
beschleunigt gesucht: v
zu c.) gegeben: v = 22 m/s; s = 80 m; gleichmäßig beschleunigt gesucht:
a, t Es gibt als Standardformel nur: I.) s = ½ ∙
a ∙ t2
und II.) v = a ∙ t In beiden Formeln wird zur Berechnung „t“ benötigt. „t“
ist aber nicht angegeben. Man muss also eine neue Formel aufstellen, in
der „t“ fehlt und nur die gegebenen Größen vorkommen. Hierzu kann man
eine Formel nach „t“ auflösen und diese dann in die andere
Formel einsetzen.
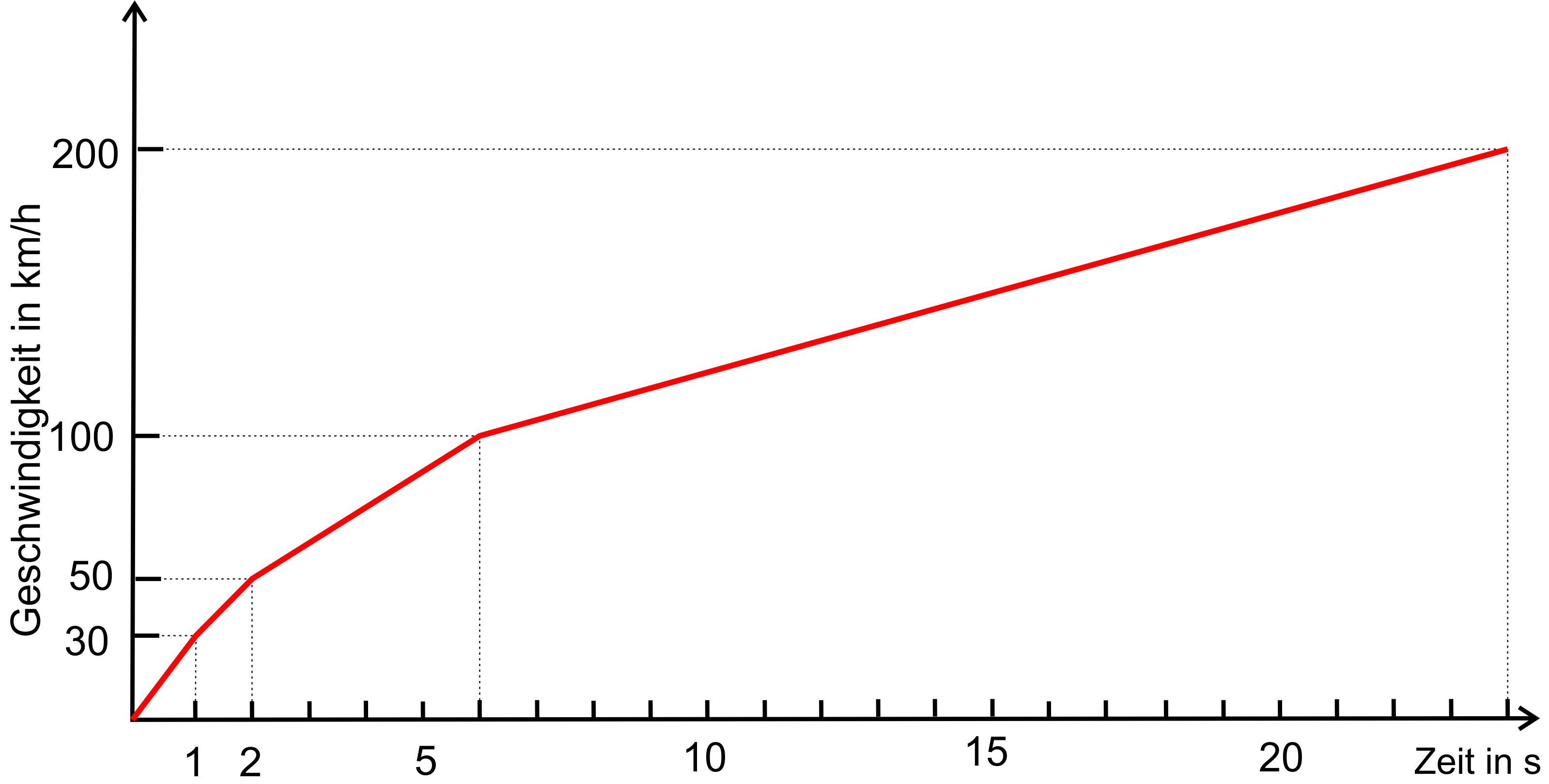
4. Klausuraufgabe Für
die Beschleunigung eines PKWs ergibt sich folgendes Diagramm:
Bestimmen
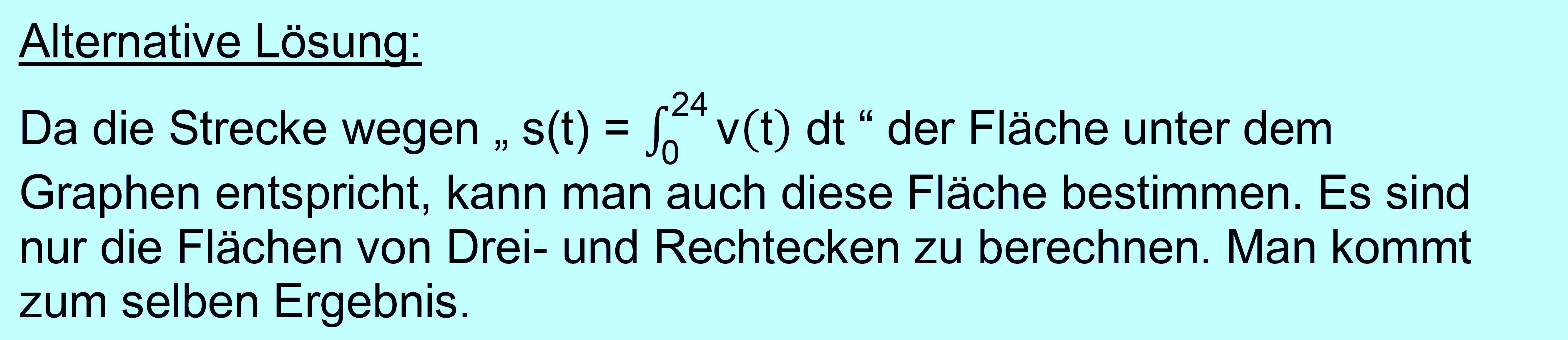
Sie die vom Start aus zurückgelegte Strecke nach 1 s. Wie
groß ist die insgesamt zurückgelegte Strecke nach 24 s? Lösung: Es liegt eine stückweise gleichmäßig beschleunigte
Bewegung vor, da v gleichmäßig mit t zunimmt (geradliniger Verlauf). Der Start liegt bei t = 0 s mit v0 = 0 m/s und s0
= 0 m. Man kann also für die erste Fragestellung die folgenden Formeln benutzen:
zurück zu zum vorherigen
Kapitel zum nächsten
Kapitel zurück zur |