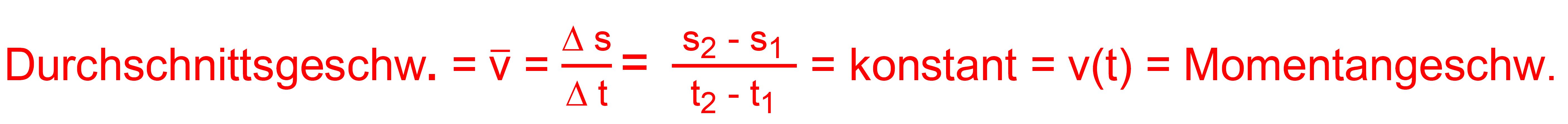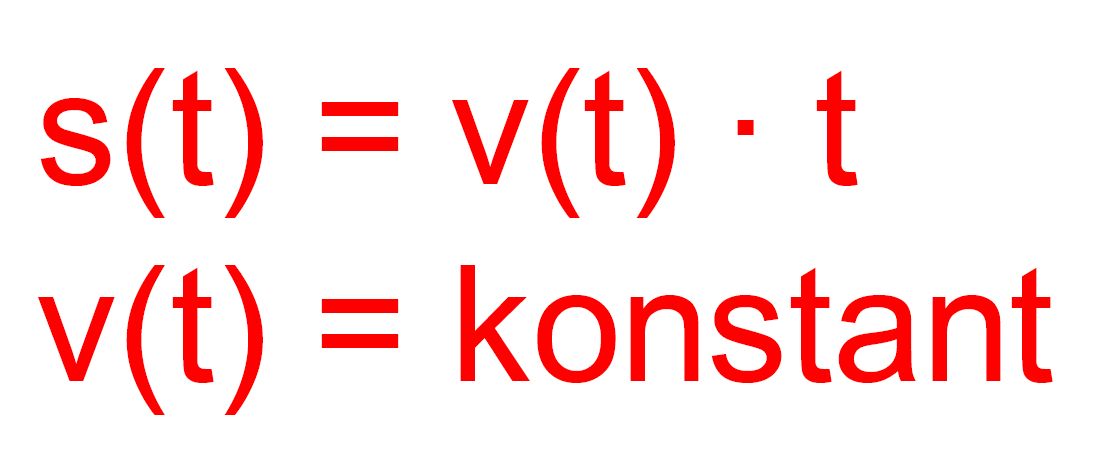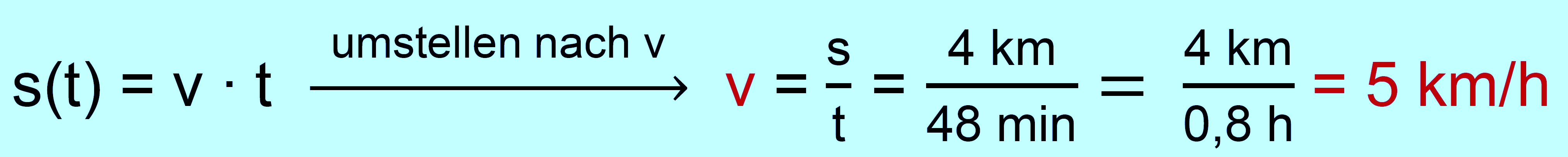|
Untersuchung
einfacher Bewegungen Gleichförmige
(geradlinige) Bewegung Unter einer
gleichförmigen Bewegung versteht man eine Bewegung bei der die
Geschwindigkeit konstant bleibt. Es findet also keine Be-schleunigung
statt. Um keine Probleme mit der Kreisbewegung
zu bekommen, wird die Geradlinigkeit häufig noch betont. Ganz korrekt müsste
man also sagen, dass bei dieser gleichförmigen (geradlinigen) Bewegung
die Geschwindigkeit vom Betrag und der Richtung kon-stant
bleibt. Dies berücksichtigt, dass die Geschwindigkeit eine vektorielle Größe
ist. Zur Untersuchung
einer gleichförmigen Bewegung kann man z. Bsp. folgendes Video
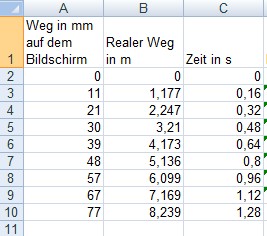
benutzen, wobei man das weiße Auto auswerten muss. [Man muss bei der Auswertung am
Bildschirm die Kalibrierung (Umrechnung) beachten, deshalb ist die Länge des grauen PKWs
angegeben] Eine mögliche
Auswertung könnte so aussehen:
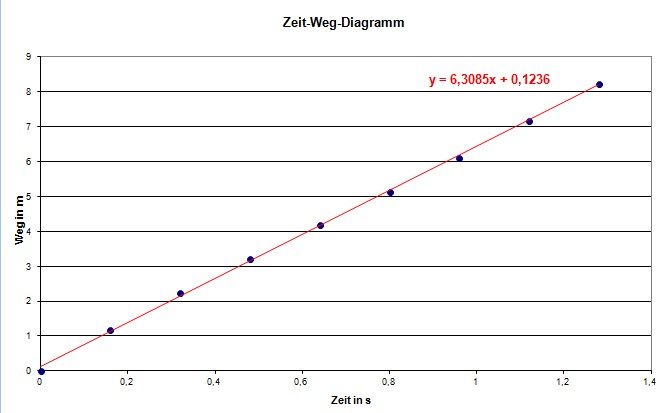
Im Idealfall muss bei
einer gleichförmigen Bewegung sogar eine Ur- sprungsgerade auftreten, wobei s =
0 m dem Startpunkt des Be- obachtungsbeginns (
t = 0 s ) entspricht. Wir wollen jetzt den Idealfall betrachten, also von
einer Ursprungsgeraden ausgehen. Bestimmt man dann für
beliebige Zeitintervalle die Durchschnittsgeschwindig- keiten ergibt sich immer
der gleiche Wert, da die Durchschnittsge- schwindigkeit der Steigung der
Geraden entspricht und diese sich ja bei einer Geraden
nicht ändert. Was ist jetzt aber
mit der Anzeige des Tachometers? Der Tacho- meter gibt die sogenannte
Momentangeschwindigkeit an, also die Geschwindigkeit zu
einem bestimmten Zeitpunkt. Wenn sich die Durchschnittsgeschwindigkeit
nie ändert, egal welches Zeitintervall man wählt, dann darf
sich natürlich auch die Momentangeschwindig- keit nicht ändern. Diese Momentangeschwindigkeit
v (t) entspricht somit der
Durchschnittsgeschwindigkeit.
Wir kommen jetzt zur
Mathematik. In der Mathematik ergibt sich für eine Ursprungsgerade
die Funktionsgleichung f(x) = m x. In unserem Fall für die Abszisse
t und die Ordinate s die Funktionsgleichung s = m t . Da m = v(t) =
Steigung der Geraden = Durchschnittsgeschwindigkeit ist, gilt also für
die gleichförmig geradlinige Bewegung die Bewe- gungsgleichungen
Da v(t) = konstant,
d.h. gar nicht von der Zeit abhängt, schreibt man häufig auch statt
v(t) einfach v auf, so dass dann gilt
Falls der Körper zum Zeitpunkt
t = 0 s schon eine gewisse Weg- strecke s0 zurückgelegt
hat, gilt die Bewegungsgleichung
|