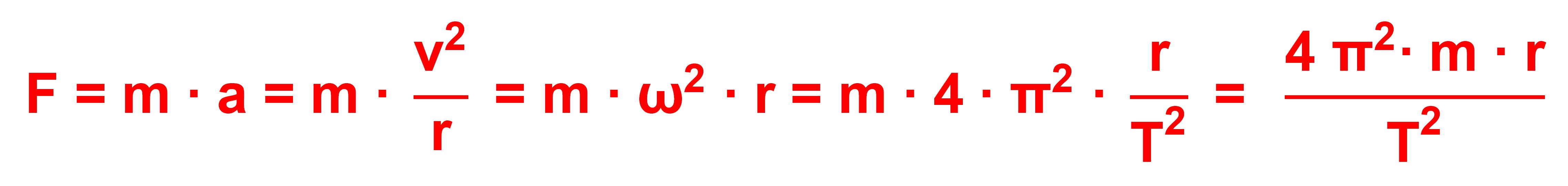|
Kreisbewegungen Eine
Kreisbewegung ist natürlich die Bewegung einer Masse m auf einer
Kreisbahn. Zur Erinnerung: Ein Kreis ist eine Linie, deren Punkt alle einen
festen Abstand r (Radius) zu einem vorgegebenem Punkt
M
(Mittelpunkt) haben. Wir wollen uns die einfachste
Kreisbewegung ansehen, nämlich die gleichförmige Kreisbewegung. Gleichförmige Kreisbewegung
Bahngeschwindigkeit Hier taucht der Begriff „Bahngeschwindigkeit“
auf. Was ist damit ge- meint? Dies ist natürlich die
Geschwindigkeit, die die Masse auf der Kreisbahn aufweist. Das Besondere bei der
Kreisbewegung ist, dass es jetzt sehr wichtig wird, dass die
Geschwindigkeit eine vektorielle Größe ist, d.h. das jetzt neben der Länge des
Vektors (also seinem Be- trag) auch die Richtung zu beachten ist. Welche Richtung weist der Vektor auf und wie
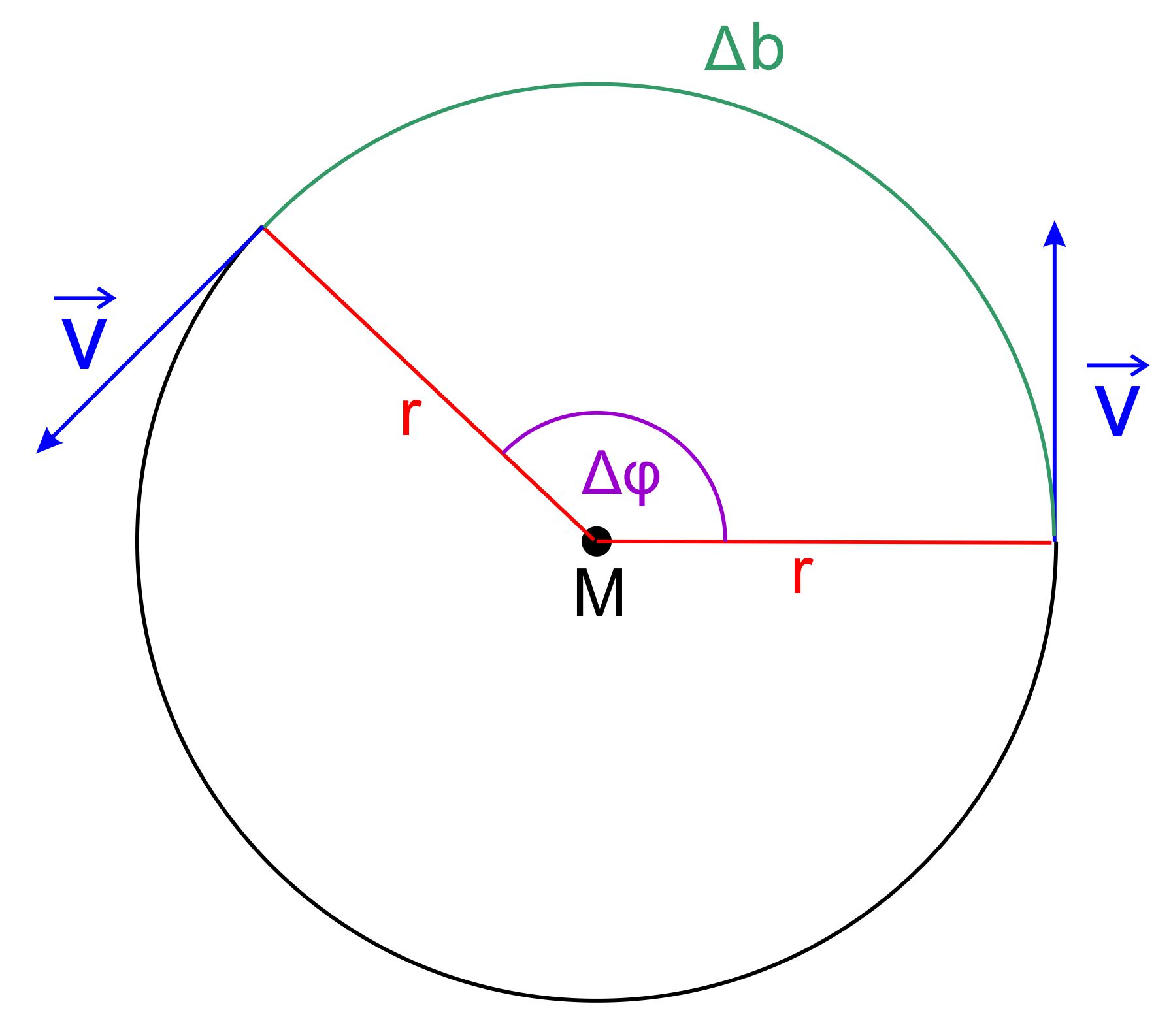
berechnet sich sein Be- trag? Die Richtung des
Vektors entspricht der Bewegungsrichtung. Aber in welche Richtung bewegt
sich eine Masse in einem Punkt auf der Kreis- bahn? Am besten man
stellt sich dazu die Umgebung um die Masse stark vergrößert vor.
Dann geht die Krümmung der Kreisbahn immer mehr in eine Gerade
über und wird schließlich zu einer Tangente an den Kreis in diesem
Punkt. Die Bahngeschwindigkeit zeigt also tangen- tial zur Kreisbahn. Der Betrag der
Bahngeschwindigkeit berechnet sich so wie bisher über die zurückgelegte
Strecke in einen bestimmten Zeitraum:
Die Momentangeschwindigkeit wird hier
„Bahngeschwindigkeit“ genannt. Die zurückgelegte Strecke ist hier die Länge
des Kreisbogens Δb, der in der Zeit Δt zurückgelegt wird.
Es gilt also:
Im Allgemeinen wird
die Kreisbewegung mindestens über einen Voll- kreis gehen, so dass
dann gilt:
Bei den Formeln wird
nur auf den Betrag der Bahngeschwindigkeit ein- gegangen, der ja bei einer
gleichförmigen Kreisbewegung konstant ist, so dass dann gilt
v(t) = v = konstant. Winkelgeschwindigkeit Da die
Bahngeschwindigkeit von dem Radius abhängt, wird gerne bei Kreisbewegungen
eine neue Größe eingeführt, die sich Winkelge- schwindigkeit
ω (t) nennt. Für die
Winkelgeschwindigkeit ω (t) gilt:
Man
beachte, dass der zurückgelegte Winkel im Bogenmaß angegeben wird, so
dass für die Einheit gilt:
Für die
gleichförmige Kreisbewegung ist natürlich auch ω (t) konstant, also gilt
ω (t) = ω. Gehen wir
wieder davon aus, dass mindestens ein Vollkreis über- strichen
wird, kann man ω berechnen mit
Man erkennt
sofort, dass es einen Zusammenhang zwischen v und ω gibt,
wenn man sich die Formel für den Vollkreis anschaut. Es gilt
offensichtlich:
Frequenz Eine
weitere wichtige neue Größe, die bei Kreisbewegungen auftritt, ist die
Frequenz f. Die
Frequenz ist festgelegt mit:
Die
Umlaufdauer T ist ja (s.oben) die Zeitdauer für das Durchlaufen eines vollenKreises.
Wenn man also n Umläufe in der Zeit t hat, ergibt sich
folgender Zusammenhang:
Die
Bahngeschwindigkeit und Winkelgeschwindigkeit lassen sich mit f jetzt also auch so
schreiben:
Radialkraft oder Zentripetalkraft Wir kommen jetzt zum zentralen
Punkt bei der Kreisbewegung, nämlich der Zentripetalkraft.
Diese Kraft ist dafür verantwortlich, dass die Masse auf die Kreisbahn
gezwungen wird. Nach dem ersten Newtonschen Axiom, dem
Trägheitssatz, bleibt ein Körper, wenn keine
Kraft auf ihn einwirkt, in Ruhe oder in einer gerad- linigen
gleichförmigen Bewegung. Bei der Kreisbewegung, die ja nicht zu den
Bewegungsformen aus dem Trägheitssatz gehört, muss also eine Kraft herrschen. Gleichzeitig gilt
natürlich auch das zweite
Newtonsche Axiom, das einen Zusammenhang zwischen
der Kraft und der Beschleunigung aufstellt: eine Kraft führt
immer zu einer Beschleunigung. Es gilt:
Wenn es also nach
1.Newtonschen Axiom eine Kraft gibt, dann muss bei der gleichförmigen
Kreisbewegung nach dem 2.Axiom eine Be- schleunigung
vorliegen. Dies hört sich zunächst merkwürdig an, da doch die
Bahngeschwindigkeit konstant bleibt. Eine Beschleunigung liegt doch erst vor,
wenn sich die Geschwindigkeit mit der Zeit ändert. Dies sieht zunächst
nach einem Widerspruch aus. Jetzt wird es
besonders wichtig, dass die Geschwindigkeit eine vek- torielle Größe ist,
also eine Größe, bei der auch die Richtung wichtig ist und nicht nur ihr
Betrag. Ändert sich die Geschwindigkeitsrichtung, dann ist dies auch
eine Änderung der Geschwindigkeit, nämlich des Geschwindigkeitsvektors.
Bei der Kreisbewegung ändert sich laufend die Richtung des
Geschwindigkeitsvektors, da er ja immer tangential zum Kreis zeigt. Aus diesen Überlegungen
kann man auf theoretischem Weg eine Formel für die
Beschleunigung, die hier Zentripetalbeschleunigung az genannt wird,
herleiten. Wir wollen einen
praktischen Weg wählen, da uns im Allgemeinen an dieser Stelle noch
die Vektorrechnung fehlt. Praktisch heißt, dass wir die Abhängigkeit der
Zentripetalbeschleunigung von verschiedenen Größen untersuchen
und aus den Ergebnissen der Messungen eine Formel für az
aufstellen. Versuche zur Zentripetal- bzw.
Radialbeschleunigung Wir
benutzen für unsere Versuche das Handy. Jedes Handy besitzt für die
Lagebestimmung im Raum einen Beschleunigungssensor. Die Daten
dieses Sensors können über Apps ausgelesen werden. Eine sehr bekannte
App ist „phyphox“
von der RWTH Aachen. Man
braucht jetzt nur noch einen Motor, dessen Drehzahl geändert werden
kann. Dieser Motor treibt direkt oder indirekt einen Aufbau an, der aus
einer Schiene besteht, die im Kreis gedreht werden kann. Auf dieser
Schiene wird das Handy sicher befestigt. Also ein ziemlich ein- facher
Aufbau, den man z. Bsp. auch zu Hause mit einer Bohrmaschine durchführen
könnte. Messergebnisse: 1.) a in
Abhängigkeit von T, r bleibt konstant T wird mit
einer normalen Stoppuhr z.B. vom Handy gemessen. a wird in der
App. abgelesen, am besten als Mittelwert aller Messungen oder als
Mittelwert im Diagramm. Eine
Auswertung mit Excel ergibt: a gegen T gibt eine gekrümmte Linie (Hyperbelmäßig);
a gegen 1/T2 ergibt die Ursprungsgerade, also ist a proportional
zu1/T2. 2.) a in Abhängigkeit
von r, T bleibt konstant r muss von der
Drehachse bis zum Mittelpunkt des Handys gemessen werden, da der
Beschleunigungssensor genau in der Mitte des Handys angebracht ist. Die
Drehzahl wird konstant einstellt. a ist also
proportional zu r, da beim Auftrag sofort eine Ursprungsgerade auftritt. Wie üblich werden die
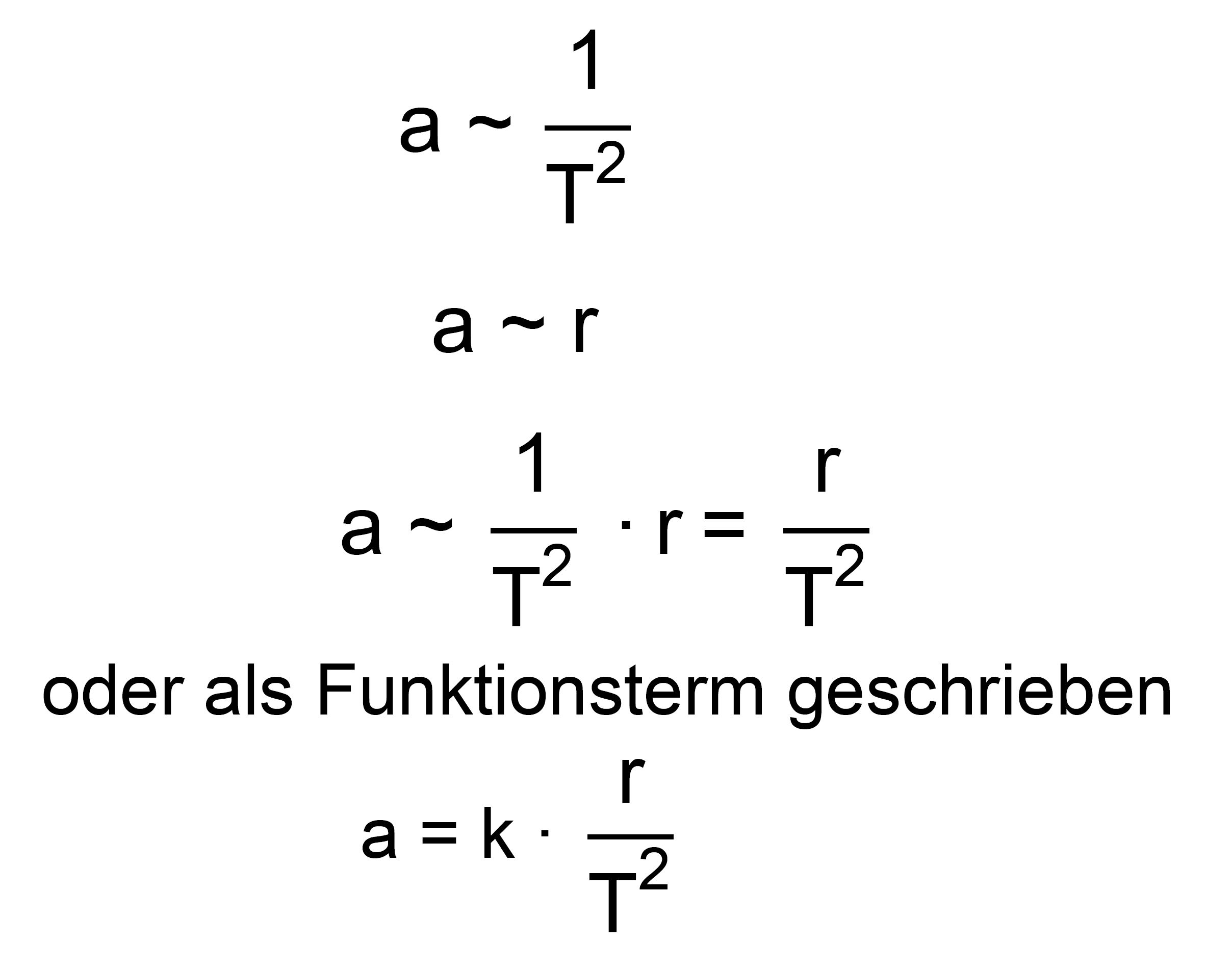
Einzelabhängigkeiten durch Produktbildung zu- sammengeführt. Es gilt also
zusammenfassend:
Es bleibt jetzt noch
übrig, die Proportionalitätskonstante k zu bestim- men. Hierzu gibt es
verschiedene Möglichkeiten: Wir wählen hierzu die
zweite Messreihe. Aus der zweiten Messreihe ergibt sich: a = kr
· r, wobei kr = k/T2 ist. Es gilt also:
Da es sich um
Versuchsergebnisse handelt, erhält man natürlich nicht den exakt richtigen
Wert für die Konstante k. Dies wäre nur mit der the- oretischen Herleitung
möglich. Wir halten also fest:
Mit der
Grundgleichung der Mechanik und dem obigen Ergebnis für a gilt also:
Für den Betrag der
Zentripetalkraft F gelten also obige Formeln. Die Kraft ist aber eine vektorielle
Größe, muss somit also eine Richtung haben, die der
Richtung der Beschleunigung entspricht ( s. Grund- gleichung der
Mechanik). Welche Richtung liegt
nun vor? Da wir uns hier nur mit der gleich- förmigen
Kreisbewegung beschäftigen, bei der ja der Geschwindigkeits- betrag sich nicht
ändert, muss die Kraft senkrecht zu v zeigen, sonst würde die Kraft zu
einer Veränderung des Betrages der Geschwindig- keit führen. Die Kraft muss also
senkrecht zum Geschwindigkeitsvektor zeigen und ist so gerichtet,
dass der Körper auf die Kreisbahn gezwungen wird. Da bleibt nur
die radiale Richtung übrig, d.h. die Kraft zeigt radial zum Mittelpunkt des
Kreises. Hier noch einmal eine
Zusammenfassung in einer Abbildung:
|