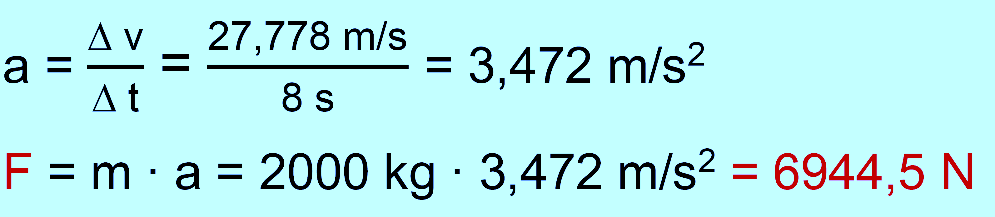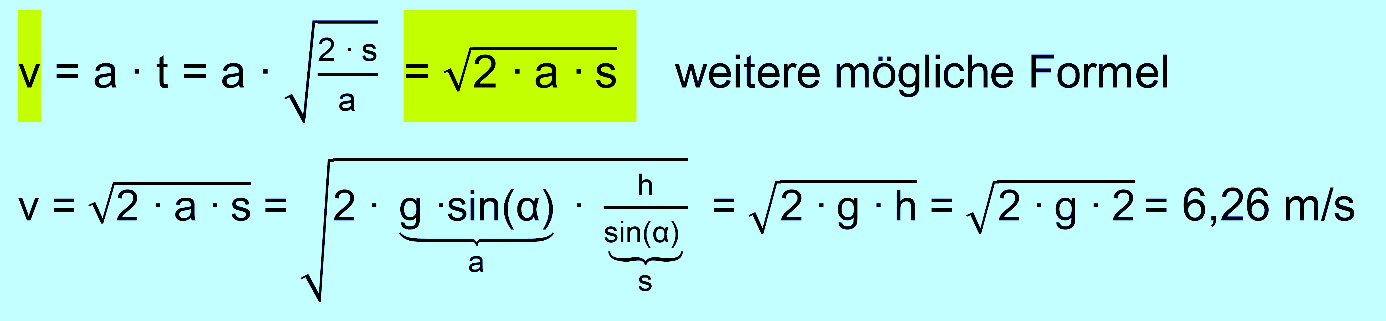|
Axiome von Newton 2.
Newtonsches Axiom oder Grundgleichung der Mechanik Dieses zweite Axiom ergibt sich zum großen Teil
aus dem ersten Axiom. Wenn ein Körper seine Geschwindigkeit
ändert, dann muss eine resultierende Kraft eingewirkt haben. Eine
Geschwindigkeits- änderung bedeutet
in der Physik, dass eine Beschleunigung statt- gefunden hat (s. gleichmäßig beschleunigte
Bewegung). Wenn also eine Kraft auf einen Körper einwirkt, kommt es zu
einer Geschwin- digkeitsänderung dieses Körpers und somit zu einer Beschleuni- gung. Das zweite Axiom
gibt genau an, wie der Zusammenhang zwischen diesen Größen aussieht.
Mit dieser Gleichung kann man jetzt die Krafteinheit 1 N gut
definieren.
Außerdem lässt sich mit dem zweiten Axiom auch
die Gleichung für die Gewichtskraft (= Anziehungskraft der Erde)
erläutern, die meist schon in der Mittelstufe besprochen wird.
Schulunterricht Experimenteller Beweis
des zweiten Axioms Obwohl es sich bei der Grundgleichung der
Mechanik um ein Axiom handelt, wird im Schulunterricht häufig versucht,
diese Gleichung herzuleiten. Dies ist ja eigentlich unsinnig, da
ein Grundsatz vorliegt, der nicht bewiesen werden kann. Daher geht bei
allen experimen- tellen Untersuchungen
des Axioms schon das Axiom ein, meist in Form der Gewichtskraft („Die Katze beißt sich in
den Schwanz“). Hierzu einige Beispiele: 1. Möglichkeit: Aufbau: Ein Schlitten wird auf einer
Luftkissenfahrbahn mittels einer Umlenkrolle mit der Gewichtskraft eines
Massestück beschleunigt. Die Beschleunigung bestimmt man über die
Zeitmessung t (Licht- schranken) für das
Zurücklegen einer vorgegebenen Strecke s (Ab- stand der Lichtschranken). Man berechnet dann die
Beschleunigung über die bekannte Formel s = 0,5 ∙ a ∙
t2. Dieses Verfahren wird in den folgenden Videos
benutzt. Das erste Video zeigt den Grundversuch, der dann im zweiten Video
verbessert wird. Man muss also beide Videos ansehen, wenn man es im
Schulunterricht richtig machen will. Hinweis zu Video 2: Der Physiklehrer versucht am
Anfang seine Fehler klein zu reden 2. Möglichkeit: Wenn im ersten Fall die Reibung über die Rolle
noch zu groß sein sollte (eigene Erfahrung), kann man auch die
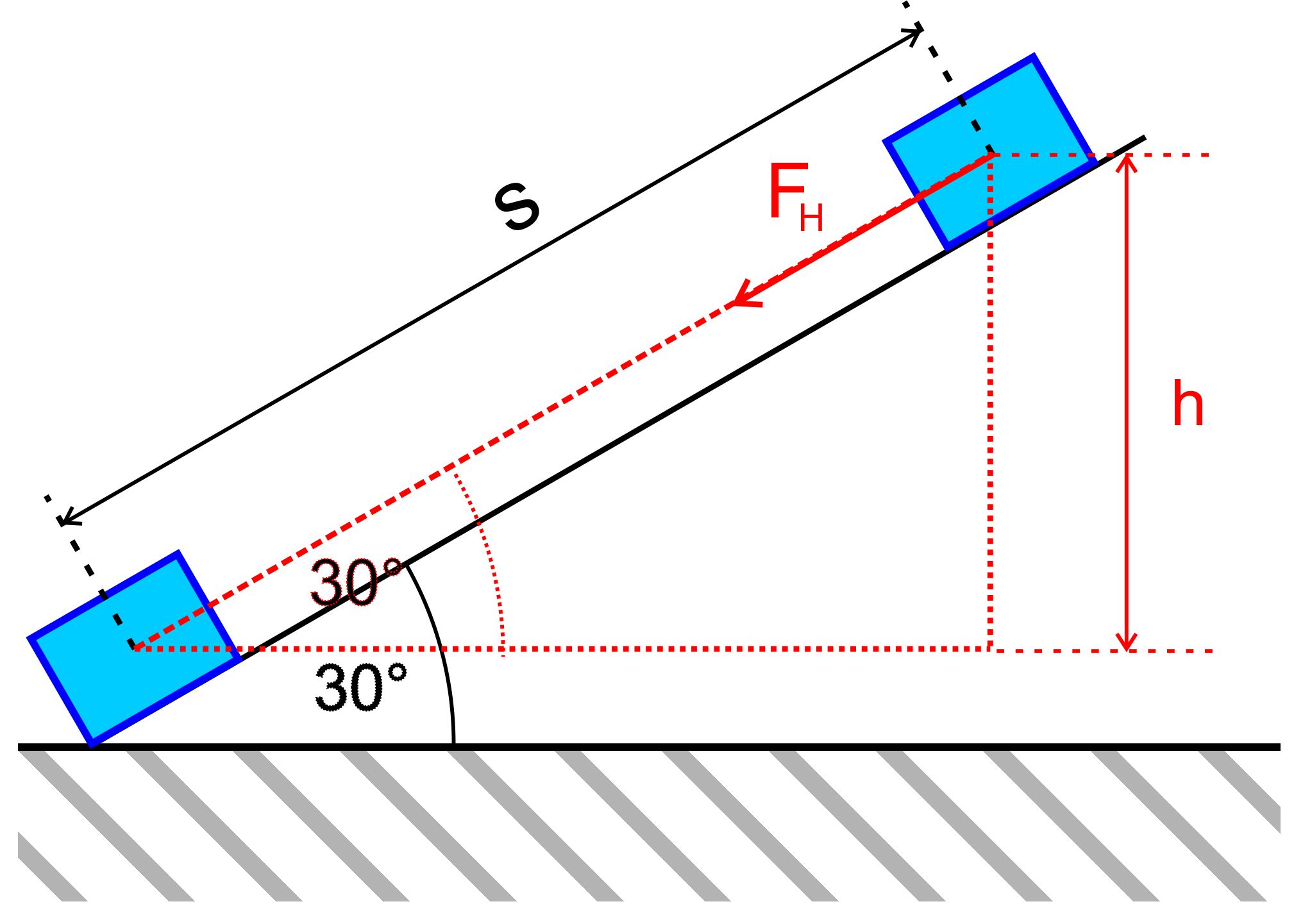
Fahrbahn schräg stel- len und über die
Beschleunigung an der schiefen Ebene den „Be- weis“ führen. Man kann das Video über
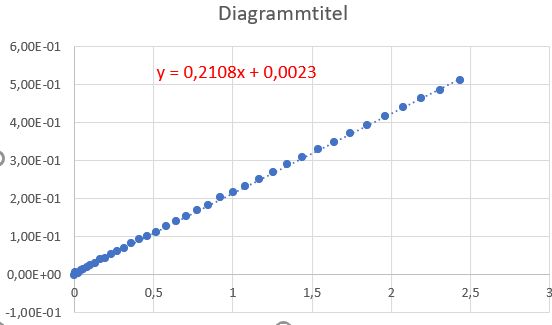
Videoanalyse untersuchen (auch im ersten Fall möglich) und dabei die
Beschleunigung (s.
gleichmäßig beschleunigte Bewegung) bestimmen. Danach kann man die Proportionalitätskonstante mit der Masse
des Schlittens ver- gleichen und erhält nahezu denselben Wert. Die
beschleunigende Kraft ist hier die Hangabtriebskraft FH
= FG ∙ sin(α). α kann man z.Bsp. über die App
„Wasserwaage“ mittels eines Handys messen. Auch hier ein Video und daneben die Auswertung
mit Excel.
|