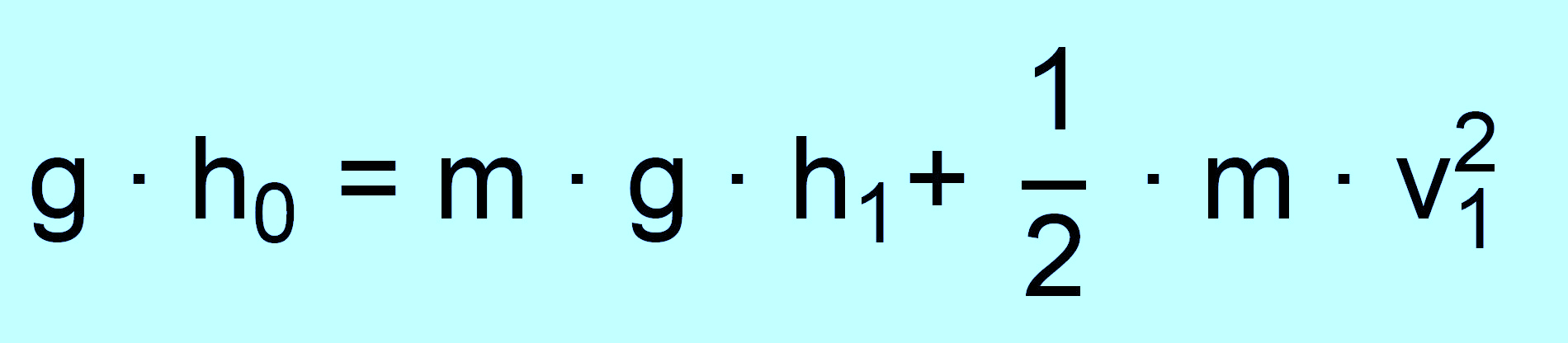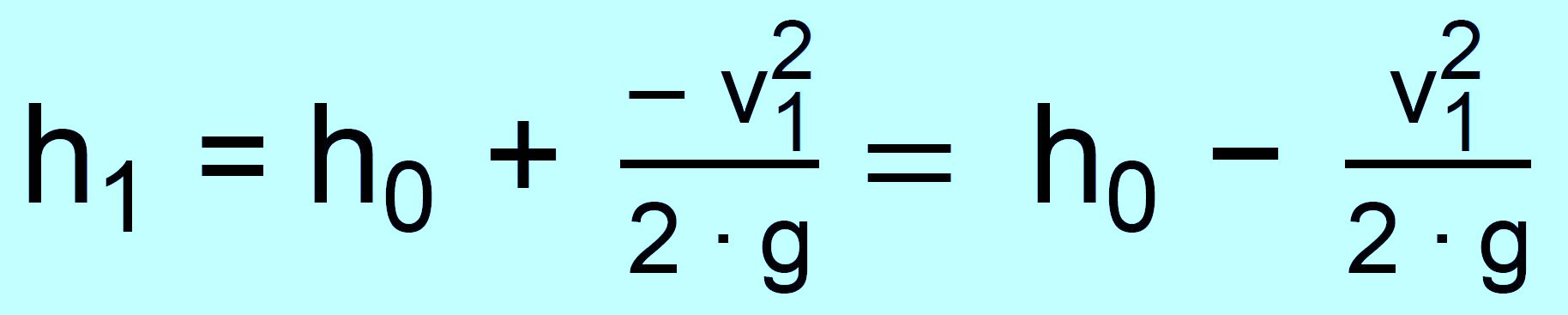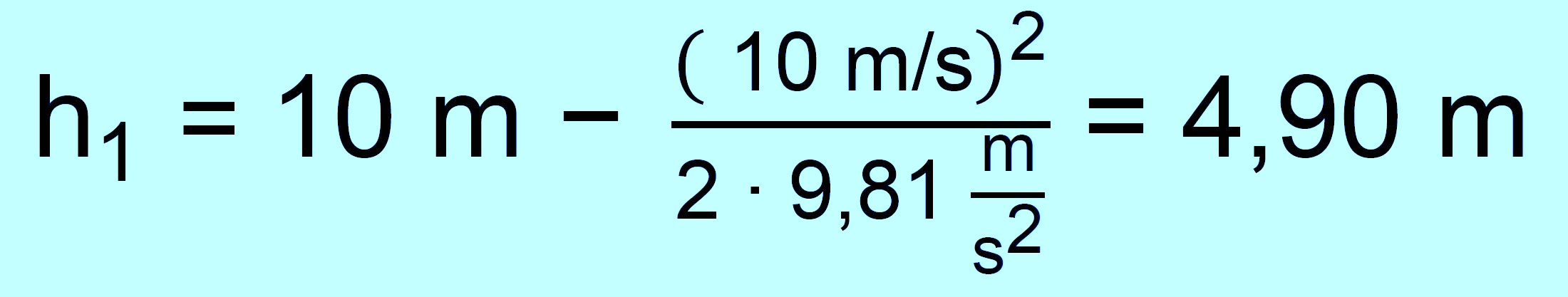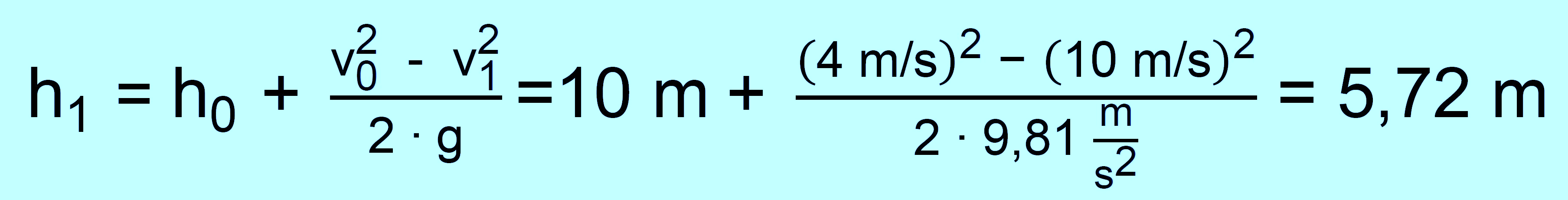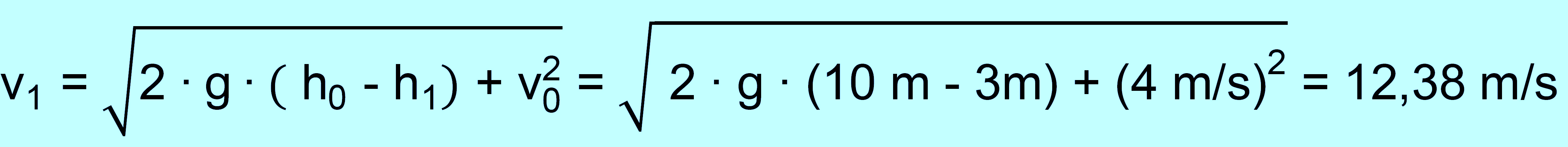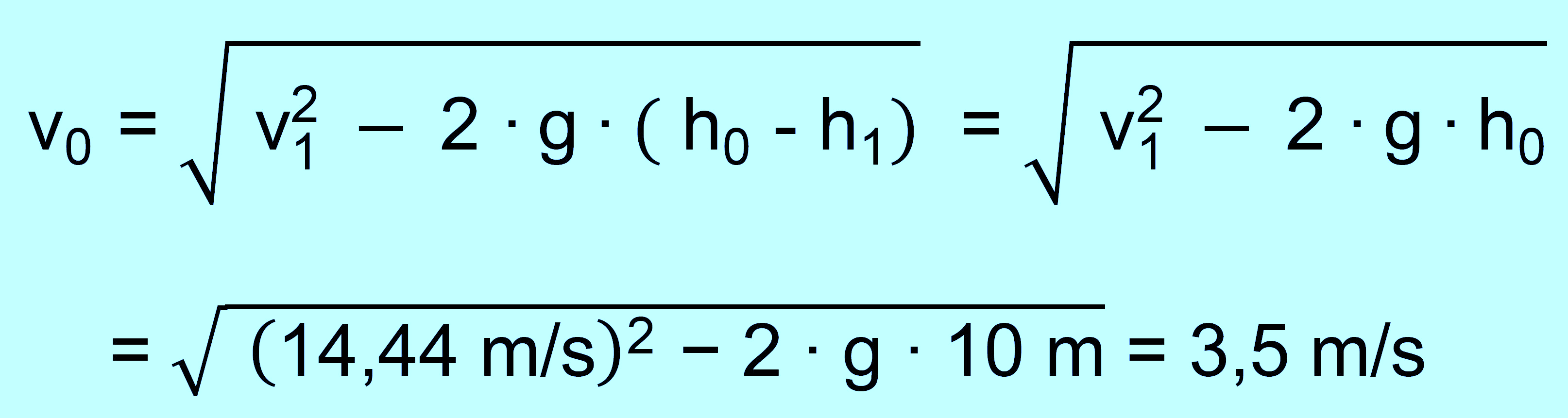|
1. Aufgabe: es gibt nur potentielle
und kinetische Energie
Herleitung einfacher
Formeln
|
Vorgabe: zum
Startzeitpunkt t0 gibt es nur kinetische und potentielle
Energie.
Es findet nur eine Umwandlung innerhalb dieser Energie-
formen
statt.
Es
gilt somit:

|
Zu der Herleitung der Formeln und der
Berechnung von Übungsaufgaben gibt es auch ein Lernvideo, das man
hier findet: Lernvideo
Zu den einfachen Formeln jetzt entsprechende
Aufgaben.
1.1. Freibadaufgabe: nach h1 gefragt
In einem Freibad springt eine Person vom 10 m Brett
a.) ohne Anlauf
b.) mit einem Anlauf (v0 = 4 m/s)
In welcher Höhe weist die Person eine
Geschwindigkeit von 10 m/s
auf? Gerechnet wird für beide Fälle.
Lösungen:
zu a.) ohne Anlauf bedeutet, dass er sich einfach
„runterplumpsen“
lässt, somit keine Anfangsgeschwindigkeit aufweist.
Die kinetische
Energie ist also zum Zeitpunkt t0 nicht
vorhanden.
Die „Grundgleichung“ lautet dann:
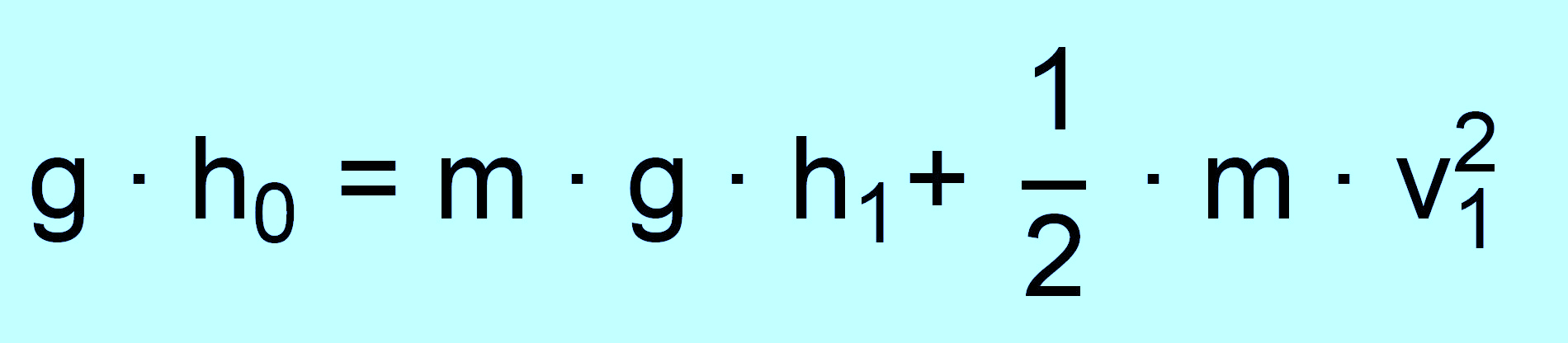
Die Formel für h1 wird dann zu:
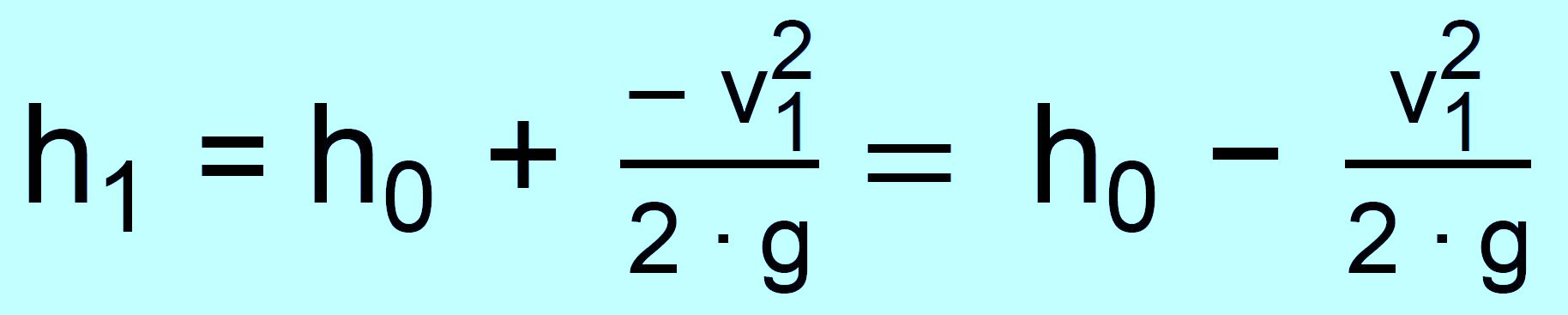
Einsetzen ergibt also:
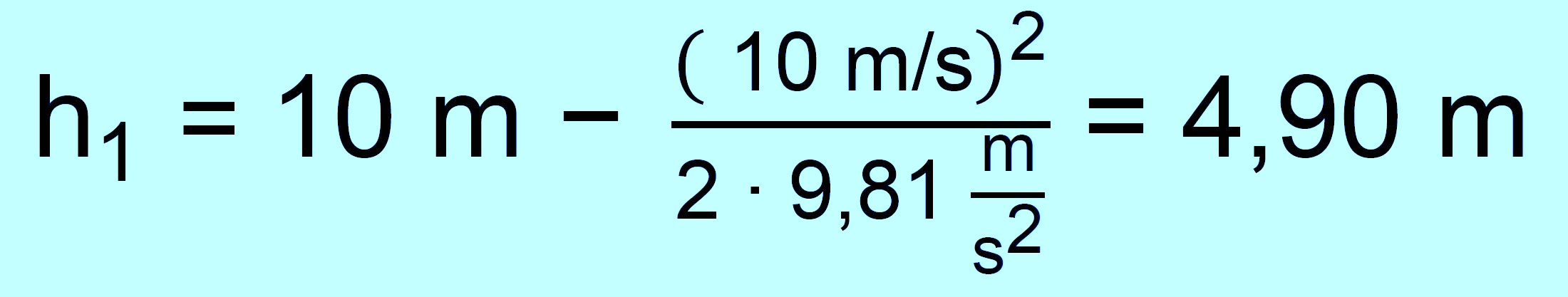
zu b.) diesmal gilt die „Grundgleichung“ vollständig
und somit auch die
vollständige Lösungsformel, also:
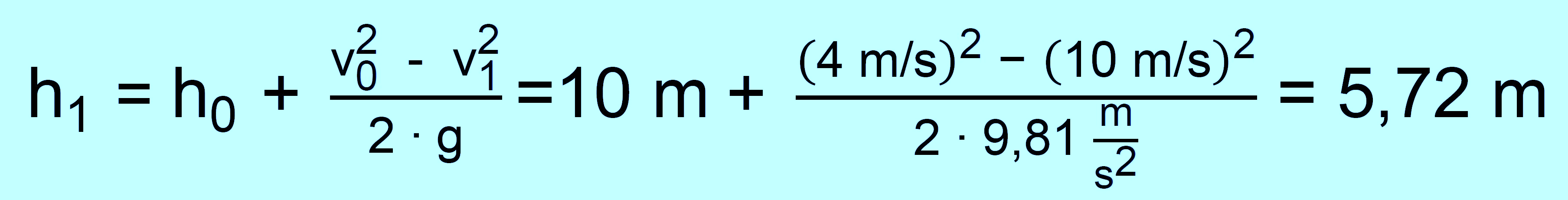
Wir ändern die Fragestellung jetzt etwas.
1.2. Freibadaufgabe: nach v1 gefragt
In einem Freibad springt eine Person vom 10 m Brett
a.) ohne Anlauf
b.) mit einem Anlauf (v0 = 4 m/s)
Welche Geschwindigkeit weist die Person in einer
Höhe von 3 m auf?
Lösungen:
zu a.) s. oben: v0 = 0 m/s; Ekin,0
= 0 J
vereinfachte „Grundgleichung“ gilt (s. oben)
vereinfachte Lösungsformel und Ergebnis:
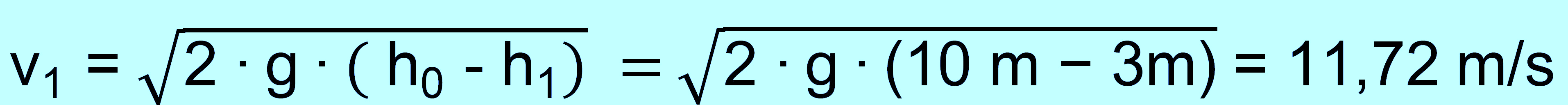
zu b.) s. oben
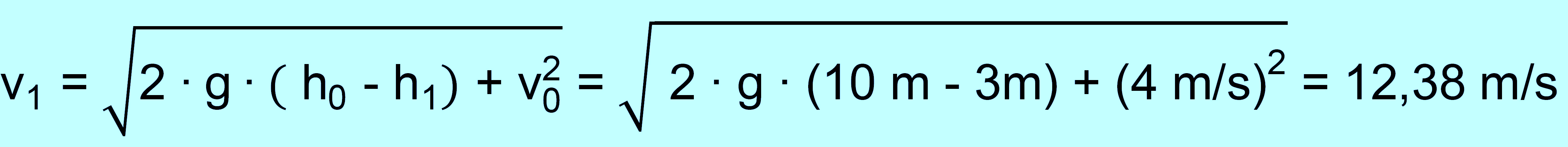
1.3. Freibadaufgabe: nach v0 gefragt
In einem Freibad springt eine Person vom 10 m
Brett.
Die Person weist beim Eintauchen eine
Geschwindigkeit von
14,44 m/s auf?
Wie groß war die Anlaufgeschwindigkeit?
Lösung:
Es ist nach v0 gefragt. v1 ist diesmal
mit 14,44 m/s bekannt. Man muss
die „Grundgleichung“ nach v0 umstellen. h1
= 0 m, da wir uns auf der
Wasseroberfläche befinden. Es ergeben sich folgende
Formeln und
Ergebnisse:
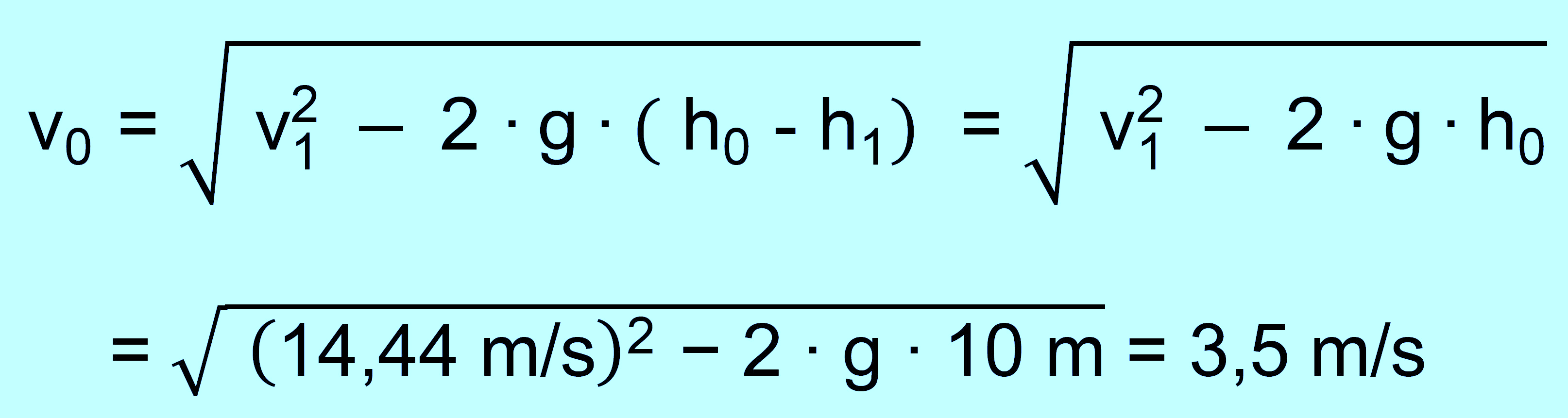
1.4. Wurfaufgabe: nach h0 gefragt
Wir haben ja schon den schiefen Wurf
kennengelernt und gesehen,
dass hier recht komplizierte Formeln auftreten. Man
muss ziemlich
viele Größen kennen, um andere Größen berechnen zu
können.
Der Energieerhaltungssatz verhilft uns jetzt dazu,
dass manche
Größen, wie Höhen und Geschwindigkeiten, sehr
einfach mit hiermit
bestimmt werden können.
Hierzu folgendes Beispiel:
Ein Ball aus einer Höhe h0 schief in den
Raum mit einer Anfangsge
schwindigkeit von v0 = 10 m/s
geworfen. In einer Höhe h1 = 2,76 m
weist der Ball eine Geschwindigkeit von v1
= 12 m/s auf. Aus welcher
Höhe wurde der Ball abgeworfen?
Lösung:
Zunächst wird man vielleicht meinen,
dass einige wichtige Größen,
wie die Masse und der
Abwurfwinkel fehlen. Die Masse spielt bei den
Bewegungsgleichungen des
schiefen Wurfes keine Rolle, weil beim
„Freie Fall“ die
Fallbeschleunigung für alle Massen gleich groß ist (s.
Superpositionsprinzip).
Im Energieerhaltungssatz ist
sie aus dem gleichen Grund nicht not-
wendig. Man erkennt ja in der
Herleitung der „Grundgleichung“ (s.
oben), dass sich die Masse
herauskürzt.
Der Abwurfwinkel würde bei den
Bewegungsgleichungen zur Berech-
nung
nötig sein, spielt aber bei dem Energieerhaltungssatz keine Rolle,
da hier nur der
Höhenunterschied wichtig ist.
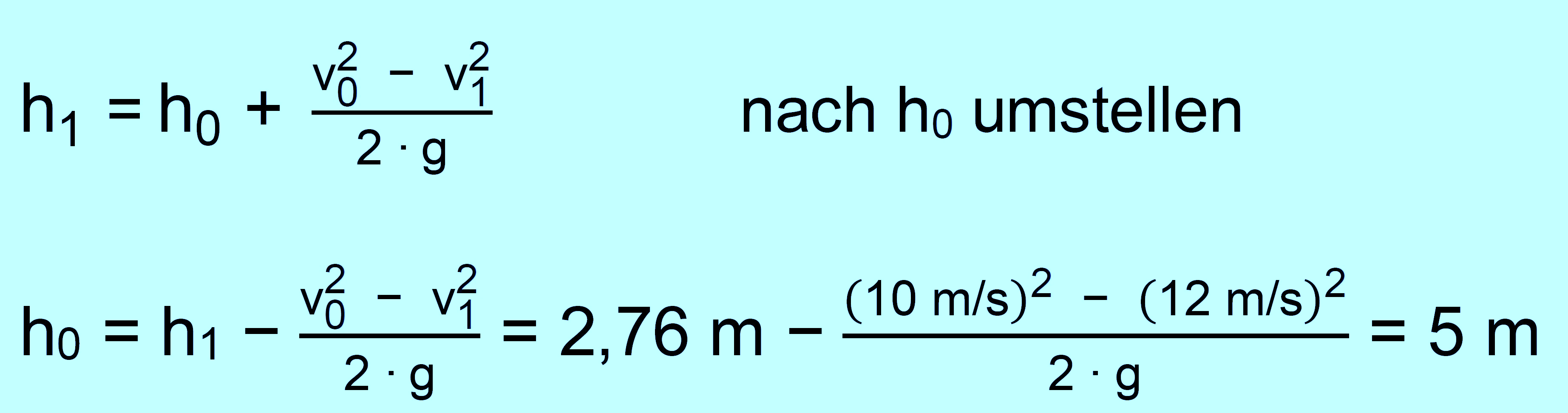
Wir setzen also mit dem
Energieerhaltungssatz („Grundgleichung“) an
und stellen nach h0
um. Er ergibt sich dann:
|
Beispielaufgaben 2.Teil
|
2. Aufgabe: alle
mechanischen Energien liegen vor
Wenn alle
mechanischen Energien in der Aufgabe vorkommen, muss
man auf die
allgemeine Energieerhaltungsgleichung zurückkehren, da
man nicht
mit „m“ teilen kann. Es gilt also:
m∙g∙h0
+ ½ m∙(v0)2 + ½ D∙(s0)2
= m∙g∙h1 + ½ m∙(v1)2
+ ½ D∙(s1)2
Folgende
Aufgabe dazu:
2.1.
Aufgabe: Airsoft-Aufgabe: Berechnung von Geschwindigkeiten
Im Geländespiel „Airsoft“ wird ähnlich dem Paintball mit
Spielzeug-
pistolen (Softairwaffen) geschossen. Als Munition dienen
kleine
Kunststoffkugeln.Die Waffe besteht im Wesentlichen aus einer Feder,
die vor dem Abschuss (Federpistole) gespannt wird.
Eine
Softairwaffe habe eine Federkonstante von 450 N/m. Es wird
Munition
mit einer Masse von 0,0003 kg benutzt. Die Feder wird um
10 cm
gespannt. Die Waffe wird waagerecht gehalten.
Hinweis: Sowohl beim Dehnen einer Feder, als auch beim Spannen
(Zusammendrücken) einer Feder gilt das Hookesche Gesetz.
a.) Mit
welcher Geschwindigkeit verlässt die Munition die Mündung der Waffe? [Zur Kontrolle: v0 = 122,4745 m/s]
b.) Die
Munition trifft mit einer Aufprallgeschwindigkeit von 122,5945 m/s auf
dem Boden auf. In welcher Höhe wurde die Waffe gehalten?
Lösung:



2.2.
Schwingende Schraubenfeder: Geschwindigkeit gefragt (extrem komplex)
Bei einer
schwingenden Feder (s. harmonische Schwingung) sieht es
auf den ersten
Blick recht kompliziert aus (s.
Energie Federschwin-
gung).
Im Folgenden
gibt es noch einmal die Ausführungen aus dem Kapitel
„Energie
Federschwingung“ in Kopie:
Beispielaufgabe
In dem Kapitel „Energie Federschwingung“
wird aber auch gezeigt,
dass man die Aufgabe deutlich schneller rechnen
kann.
Zusatzaufgaben:
- Bungee-Sprung
( sehr schwer)
- Umfangreiche Aufgabe zur Schwingungsenergie
|
|
|