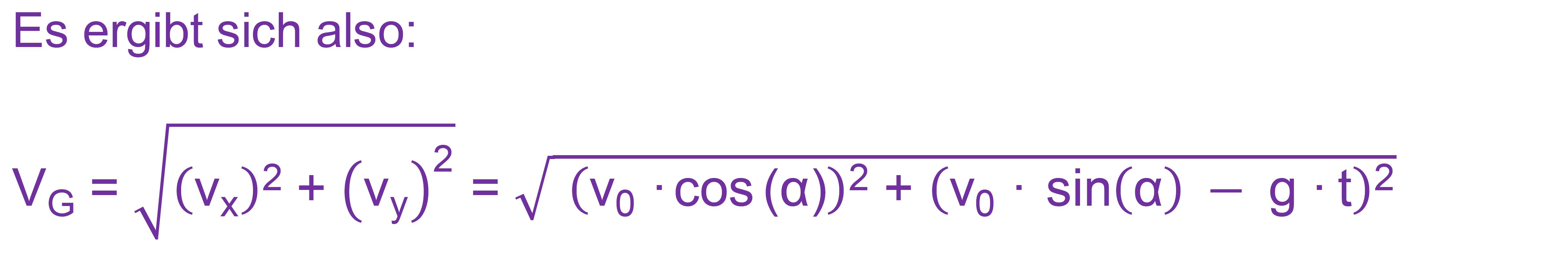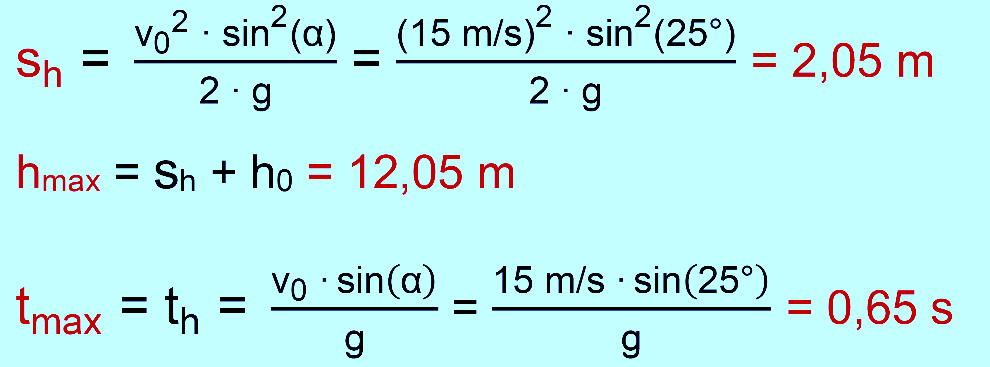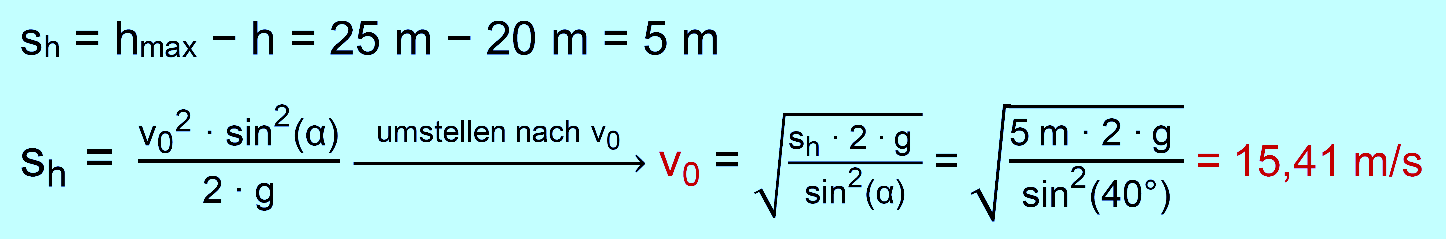|
- Beispiel 1 - Beispiel 2 - Beispiel 3 - Beispiel 4
Beispielaufgaben
1.
Beispielaufgabe (einfach)
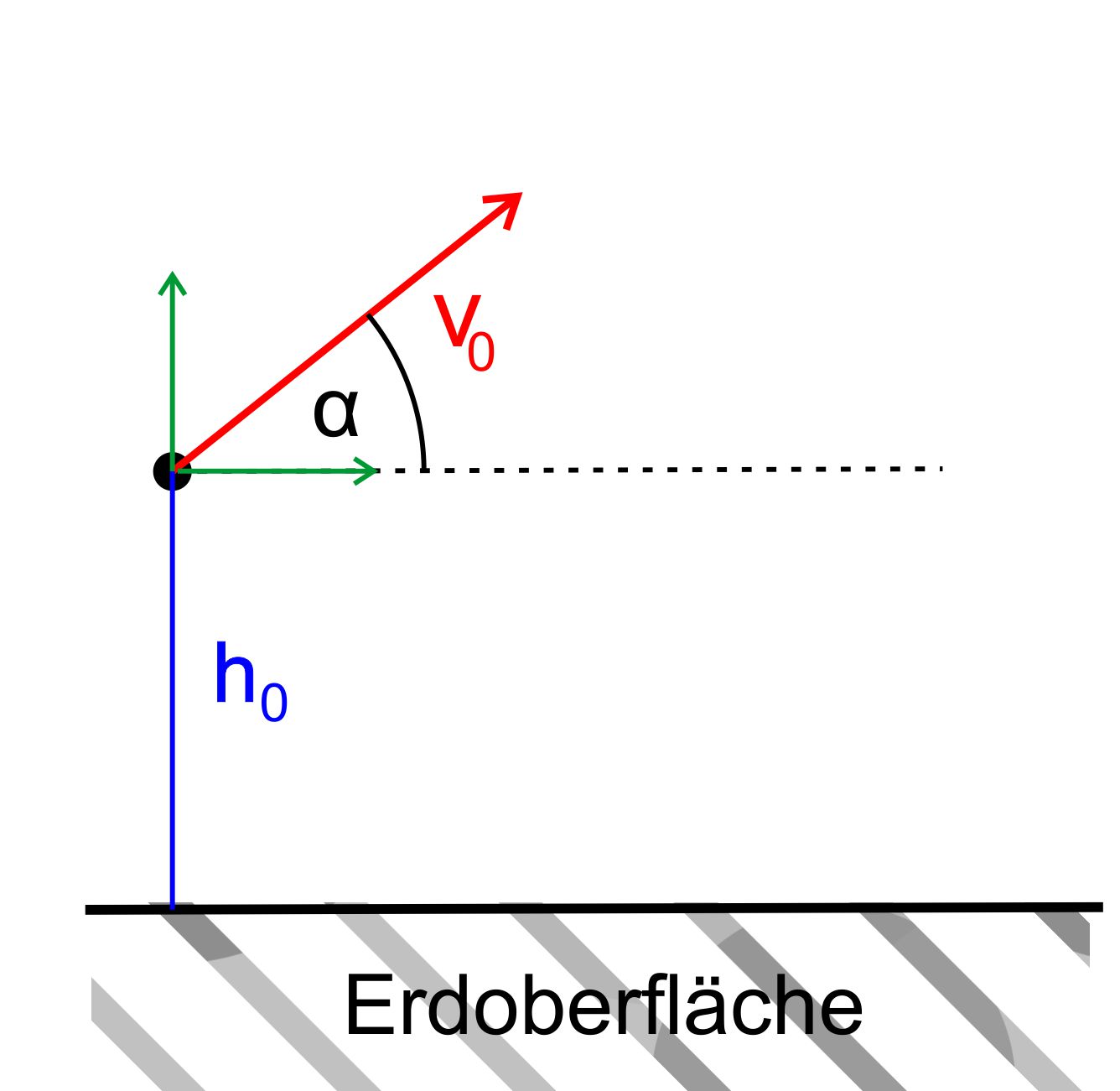
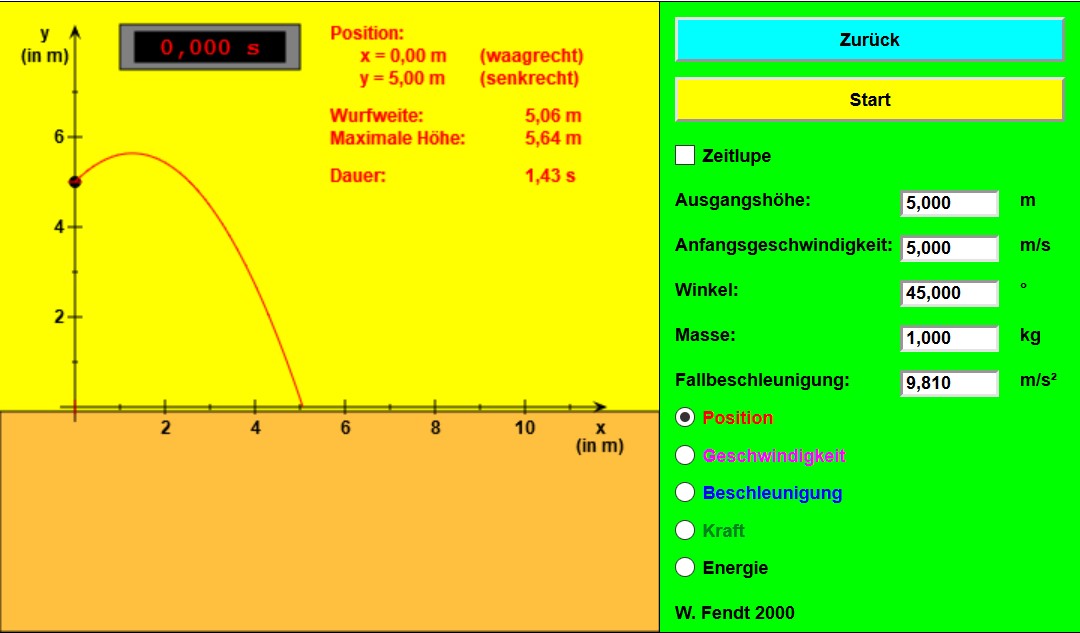
Aus
einer Höhe von 10 m wird ein Ball unter einem Winkel von
25°
mit
einer Geschwindigkeit von v0 = 15 m/s schräg abge-
worfen.
Berechnen
Sie
a.) die
maximale Höhe und die Zeit bis zu dieser Stelle
b.)
den Punkt, an dem sich der Ball nach t1 = 0,4 s, t2
= 1,4 s und
t3
= 3 s befindet
c.)
die Geschwindigkeit nach t = 1,5 s
d.)
die Zeit bis zum Aufprall auf dem Boden und die größte Weite,
sowie
den Aufprallwinkel
e.)
die Höhe, in der sich der Ball befindet, wenn er in der Horizon-
talen 20
m zurückgelegt hat
Lösung:
die
Aufgaben sind einfach, weil nur die bekannten Formeln be-
nutzt
werden
a.)
gegeben: h = 10 m; v0 = 15 m/s ; α = 25°
gesucht:
hmax; tmax
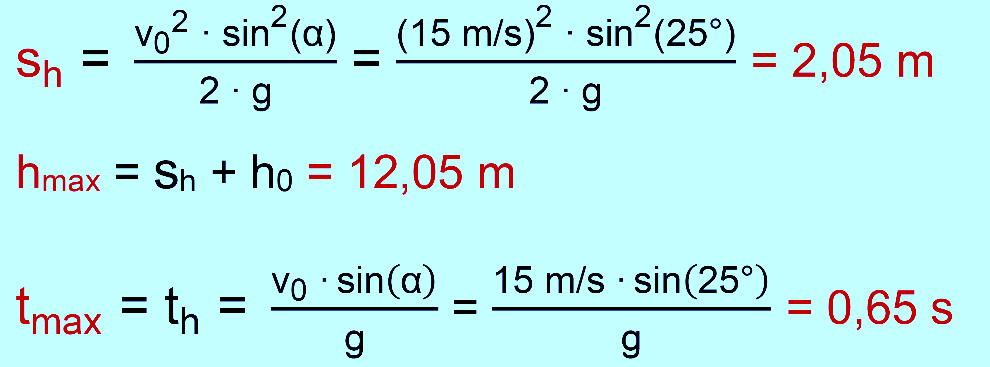
b.)
gegeben: h = 10 m; v0 = 15 m/s ;
α = 25°; t1
= 0,4 s, t2 = 1,4 s und t3 = 3 s
gesucht: Bahnpunkt P (sx
| sy)

c.)
gegeben: h = 10 m; v0 = 15 m/s ;
α = 25°; t = 1,5 s
gesucht:
v

d.) gegeben:
h = 10 m; v0 = 15 m/s ; α = 25°;
gesucht: Aufprallwinkel, größte Weite

e.)
gegeben: h = 10 m; v0 = 15 m/s ;
α = 25°; sx = 20 m
gesucht:
sy

2.
Beispielaufgabe (einfach, mittel, schwer)
Es
sind jeweils folgende Größen bekannt bzw. gesucht.
a.)
gegeben: h = 20 m;
hmax = 25 m; α =
40°
gesucht:
v0
b.)
gegeben: h = 15 m;
hmax = 18 m; v0 = 10 m/s
gesucht:
α
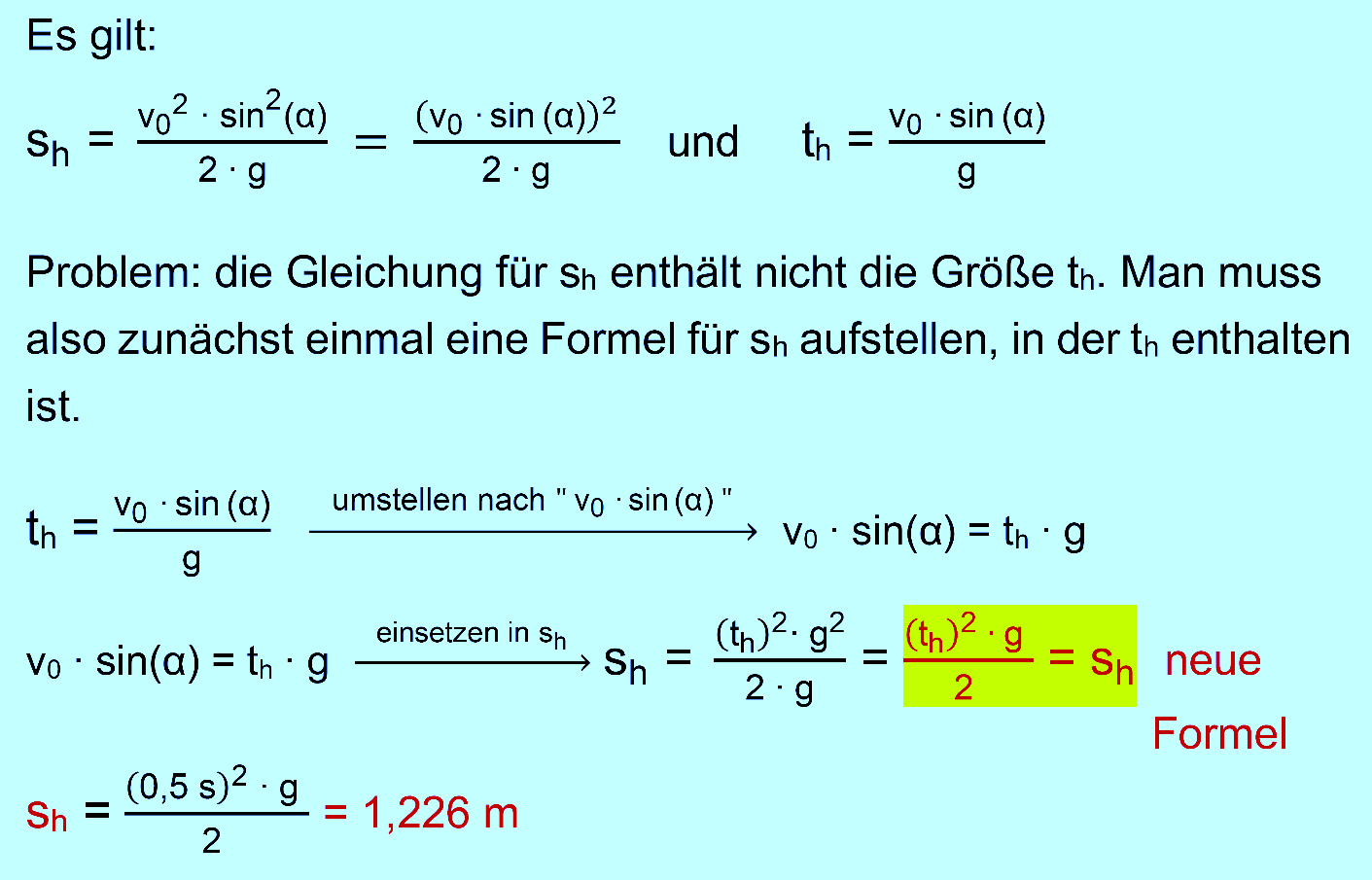
c.)
gegeben: h = 10 m;
th = 0,5 s
gesucht:
sh
Lösungen:
zu a.)
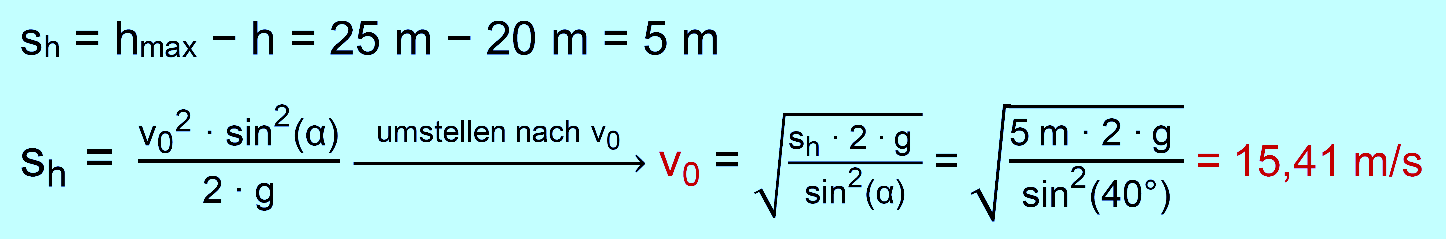
zu b.)
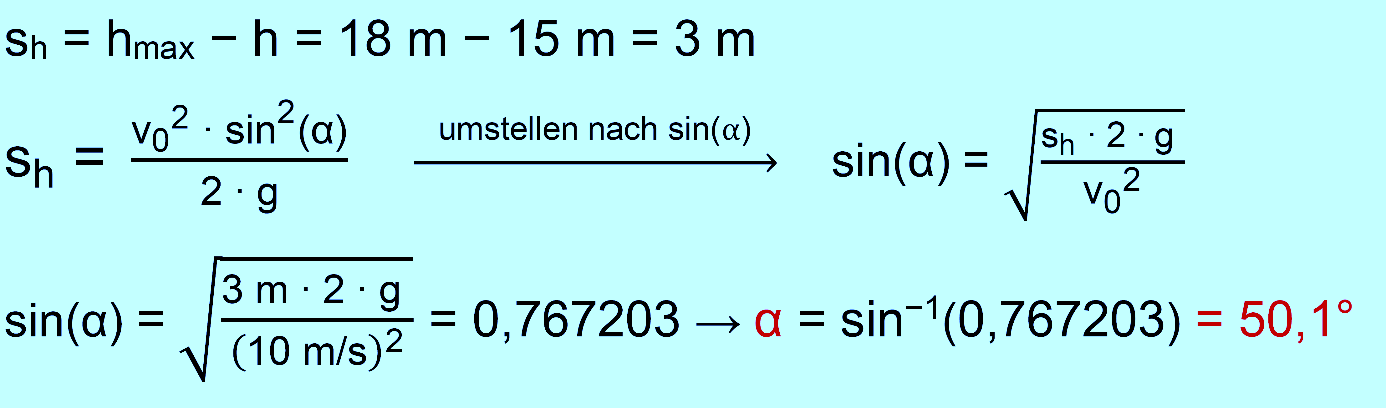
zu c.)
3.
Beispielaufgabe (mittel)
Ein
Ball wird mit v0 = 20 m/s in einem Winkel von α = 35° abge-
worfen.
Welche
Geschwindigkeit weist er bei sy = 4
m auf?
Lösung:


4.
Beispielaufgabe Kombiaufgabe (einfach)
Es
werden Sprünge auf dem 3 m − Sprungbrett betrachtet.
Hierzu
folgendes Video:

Quelle (Ausschnitt): Men's 3m Springboard Final | Rio 2016 Replay -
YouTube
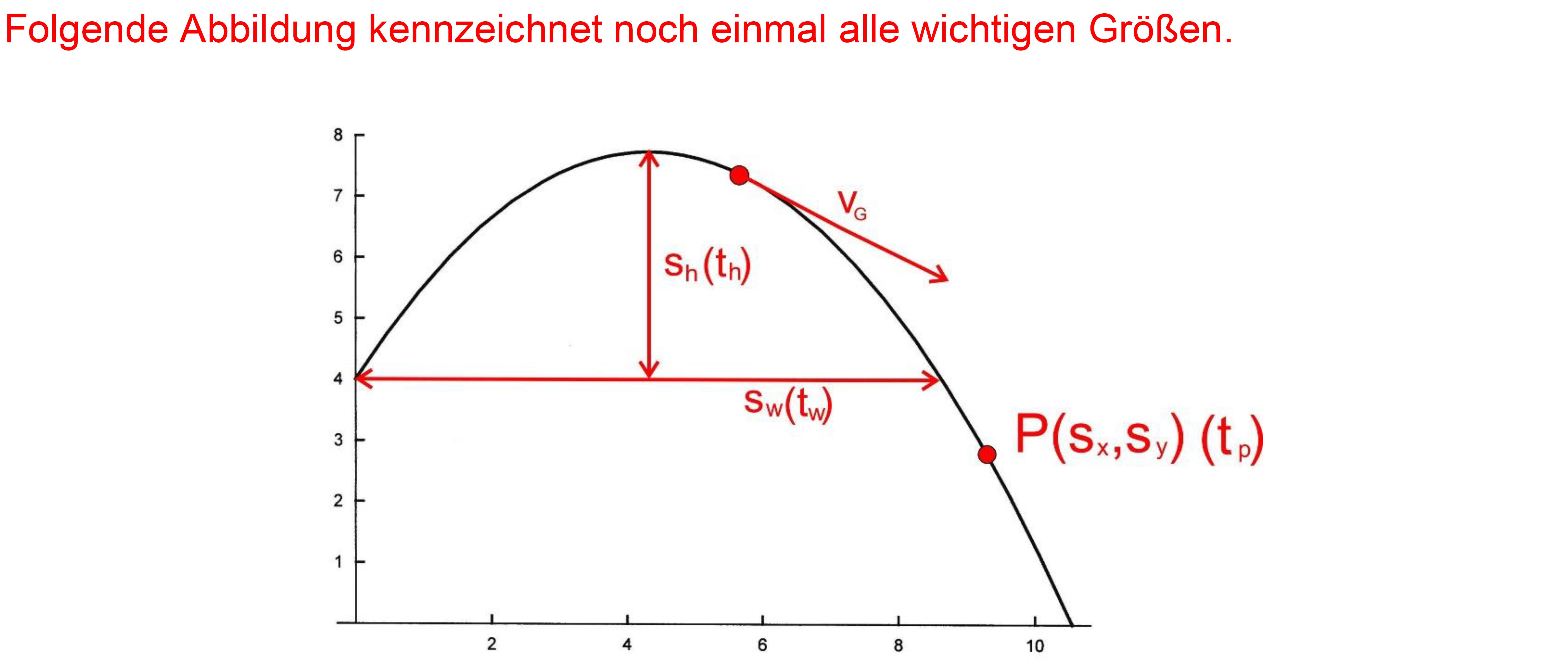
Folgende
Fälle sollen betrachtet werden.
a.)
Ein Kind geht auf das 3 m - Sprungbrett und lässt sich einfach
„herunterplumpsen“.
b.)
Das Kind nimmt jetzt Anlauf und springt mit einer Anfangsge-
schwindigkeit von 2 m vom Brett.
c.)
Ein Wettkampspringer springt vor dem eigentlichen Wettkampf-Sprung auf
dem Brett 2 m in die Höhe (s.Video)
d.)
Beim eigentlichen Wettkampfsprung springt er in einem
Winkel
von 70° ab und erreicht eine Gesamthöhe von 6 m.
Beantworte
folgende Fragen.
Mit
welcher Geschwindigkeit erreicht das Kind bei a.) bzw. b.) die
Wasseroberfläche?
Welche
Anfangsgeschwindigkeit hatten die Wettkampfspringer
in
c.) und d.)
Lösung:

- Beispiel 1 - Beispiel 2 - Beispiel 3 - Beispiel 4
|