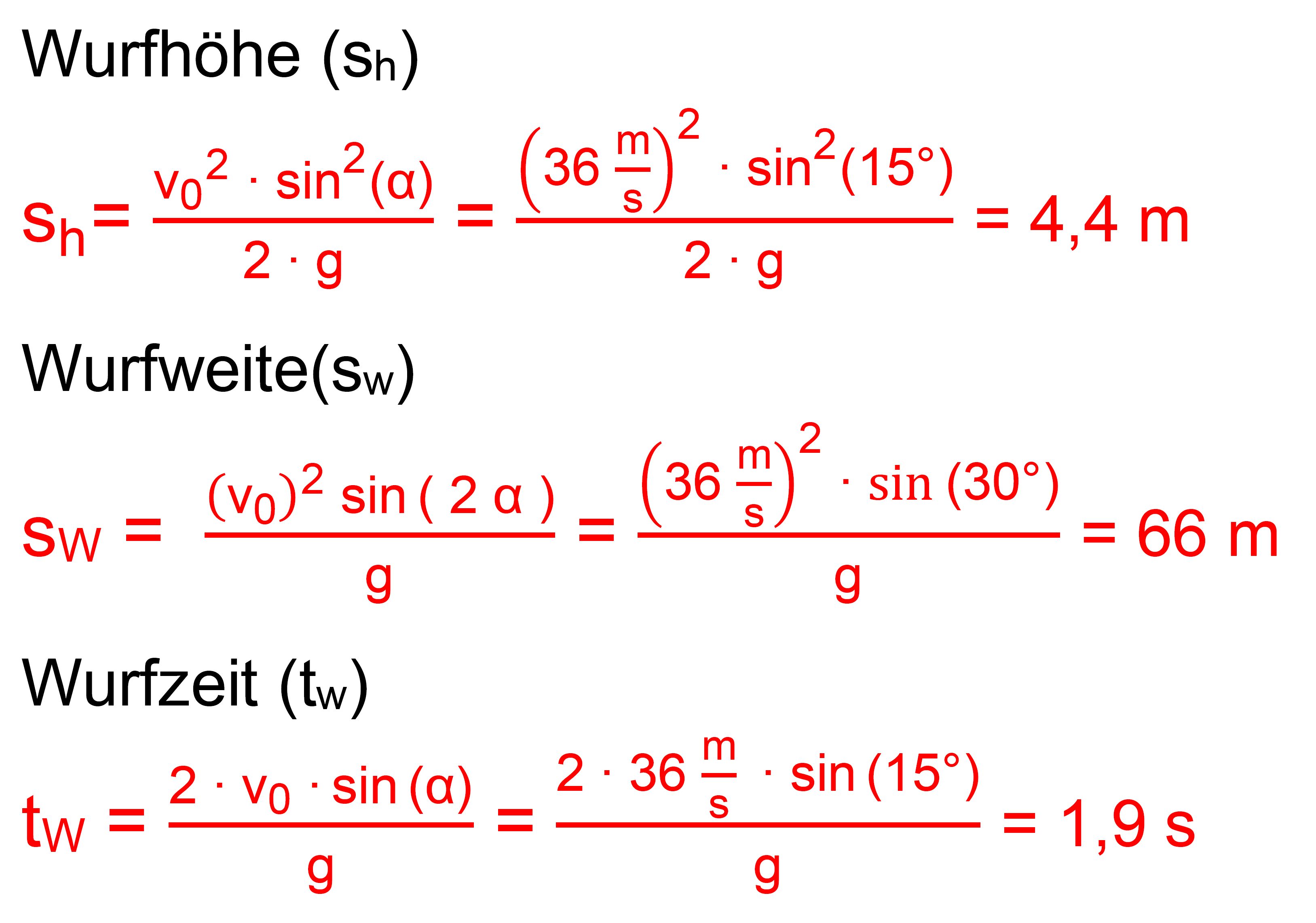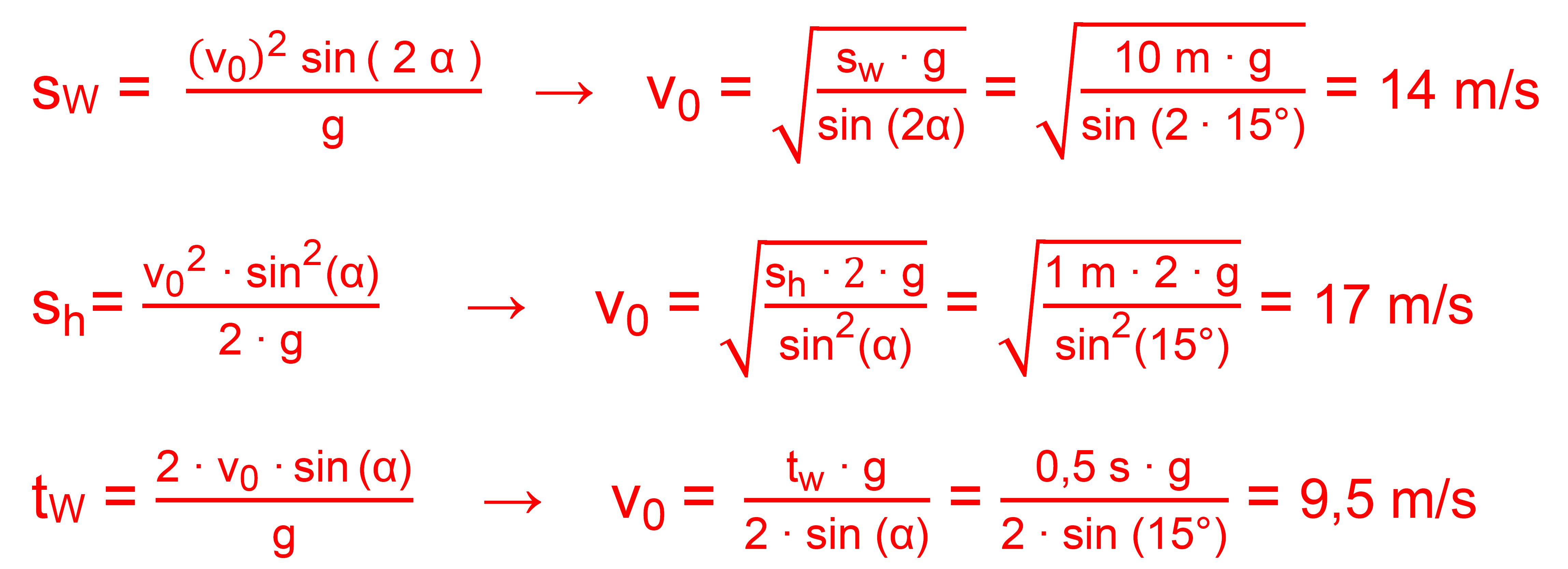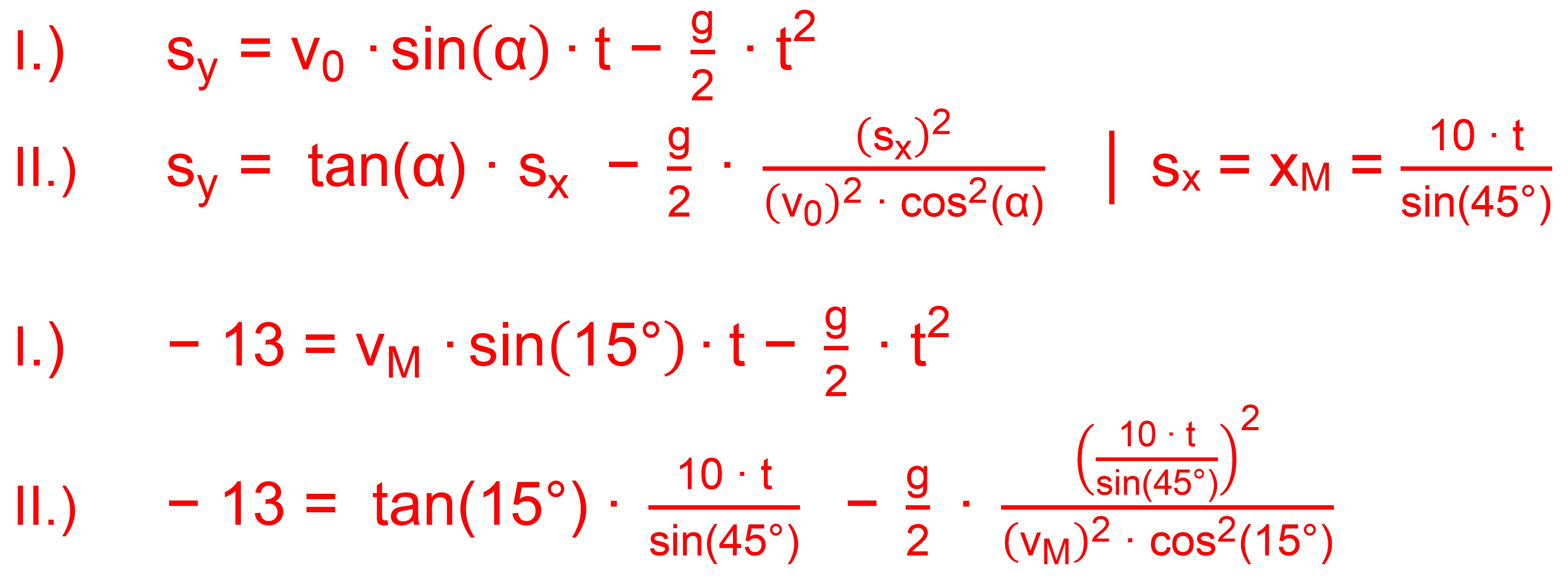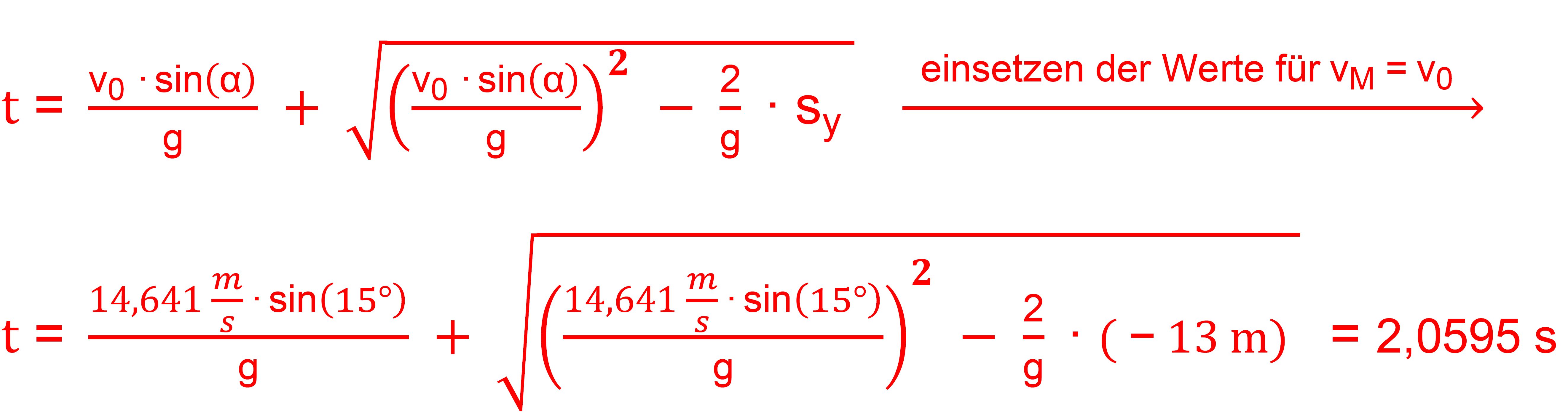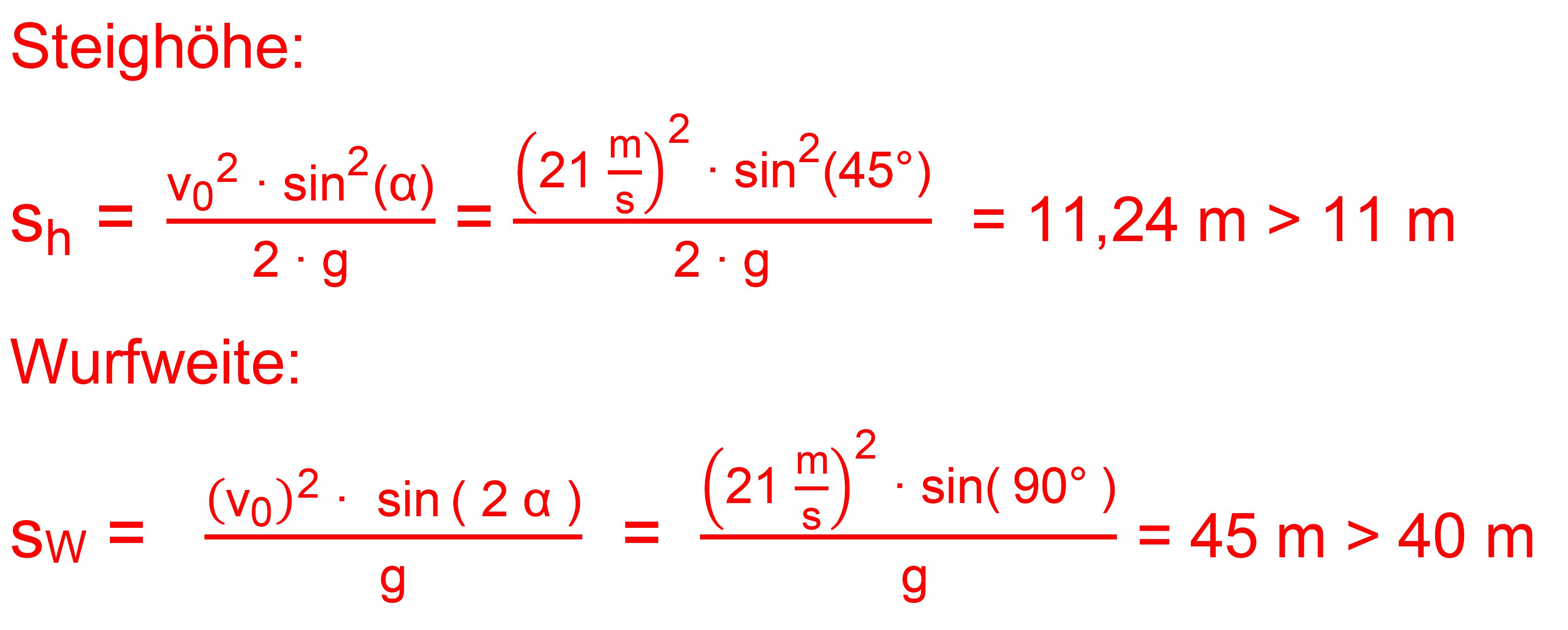|
- zur 2.
Klausuraufgabe: Sprung von der Karlsbrücke - zur 3. Kausuraufgabe.Sprung über die Scheune -
Zusatzaufgabe: Fallschirmsprung Triple X −
Physik − Sprung von der Foresthill
Bridge (mittel) In einer der ersten Filmszenen stürzt sich Vin Diesel mit einer Corvette C5 (max. Geschwindigkeit 300 km/h = 83 m/s) über das Brückengeländer der Foresthill Bridge (Gesamtlänge
= 740m) in
Kalifornien in die Tiefe, um dann mit einem Fallschirm nach unten zu schweben. Wir wollen einmal nachrechnen, - wie lange die Corvette braucht, um auf dem Boden aufzuschlagen - wie weit sie sich dabei in horizontaler Richtung bewegt, d.h. wie weit entfernt von der Brücke sie auf dem Boden aufkommt - welche Aufprallgeschwindigkeit weist die Corvette auf. Voraussetzungen: alle unsere Rechnungen finden ohne Reibung
statt! Video hierzu: Quelle: https://www.youtube.com/watch?v=NcG-rjoYiMo Lösung: Ziemlich schnell wird klar, dass es sich beim dem
Brückensprung um einen schiefen Wurf
handeln muss. Wir werden also die Gleichungen zum schiefen Wurf benutzen. Beim schiefen Wurf muss man allerdings zwei Größen
unbedingt kennen, nämlich den Abwurfwinkel α und die Anfangsgeschwindig- keit v0. Zunächst zum Abwurfwinkel: Der Abwurfwinkel kann einigermaßen gesichert aus
dem Film abge- lesen werden. Der PKW bewegt sich über eine schräg
gestellte Rampe, die aus einem Anhänger besteht, auf dem PKWs
transportiert werden. Die Oberkante der Rampe schließt ungefähr mit dem
Brückengeländer ab. Die Corvette hat eine Länge von ca. 4,6. Sie
muss also auf die Rampe passen. Wir nehmen mal in etwa eine Länge des
Anhängers von 5 m an. Das Brückengeländer muss etwa 1,3 m
hoch sein. Man erkennt dies daran, dass das Brückengeländer den Polizisten ( Video
bei t = 100 s) ungefähr bis zum
Brustkorb geht. Wir erhalten damit:
sin(α) = 1,3 m / 5 m → α = 15° Deutlich schwieriger ist es die
Anfangsgeschwindigkeit zu bestimmen. Viele Szenen haben Schnitte oder werden in Zeitlupe
abgespielt. 1. Möglichkeit: 5 s ≤ t ≤ 12 s Man sieht, wie die Corvette von mehreren
Polizeifahrzeugen auf der Brücke verfolgt wird. Die Szene dauert ca. 7 s. Der
Wagen stürzt sich ziemlich genau in der Mitte der Brücke über die
Brüstung ( t = 29 s ). Er befindet sich beim Beginn der Szene schon auf der
Brücke. Es ist schwer zu schätzen, wie viele Meter dies sind.
Abschätzung: Bis zur Corvette passen vielleicht ca. 20 PKW auf die Brücke.
Dann wären auf der Brücke ca. 20 ∙ 5 m = 100 m zurückgelegt
worden. Eine Hälfte der Brücke ist 370 m (Symmetrie im Brückenaufbau
vorausgesetzt) lang.
Die Szene endet ca. 20 m vor der Rampe. Der Wagen legt also innerhalb von 7 s eine Strecke von
ca. 250 m zurück. v berechnet sich mit: v1 = s / t = 250 m / 7 s
≈ 36 m/s = 130 km/h Dies wäre auf jeden Fall unter 300 km/h. Aber wer traut sich mit 130 km/h schräg auf eine
Rampe zu fahren, die kaum breiter als der PKW ist (t = 19 s)? Weitere
Betrachtungen führen dazu, dass mit dieser Geschwindigkeit nicht auf die
Rampe gefahren wurde. Berechnen wir nämlich einmal für v1 die Wurfhöhe, Wurfweite und Wurfzeit = 2 ∙
Steigzeit aus. Es gilt:
Die Größen beziehen sich auf den Abwurfpunkt, also
hier das Brücken- geländer. Im Video 19 s ≤ t ≤ 21 s passt hierzu
überhaupt kein Wert. Völlig utopisch ist die Wurfweite (gleiche Höhe wie
Brückengeländer)
von 66 m. Realistisch scheinen mir: sw
max. 10 m, sh max. 1 m, tw
max. 0,5 s (
tw
schwer zu schätzen, da eine Zeitlupe vorliegt). 2. Möglichkeit Berechnen wir hiermit jetzt einmal die möglichen Anfangsgeschwindig- keiten:
Man kommt zu deutlich geringeren Werten als 36 m/s. Wir wählen jetzt einmal den Durchschnittswert von
allen drei Ge- schwindigkeit und kommen auf
13,5 m/s ≈ 50 km/h. Dies scheint deutlich realistischer. Im Folgenden rechnen wir mit diesem Wert die
Aufgabe weiter: Es war zunächst nach der Flugdauer bis zum Aufprall
gefragt. Hiermit kann man dann Wurfweite w und die
Aufprallgeschwindigkeit berechnen. Es ergibt sich:
Ziemlich gesichert dürfte die Fallzeit sein, weil
diese praktisch nur von der Fallhöhe (hinterer
Teil der Wurzel) abhängt. Hierfür spielt v0 praktisch keine Rolle. 0,36 s ist übrigens die Zeit bis zum
höchsten Punkt des Wurfes. Nach Video so ziemlich nach Überquerung der
Brückenkante. tW wäre dann 0,72
s. Scheint eher zu viel zu sein, da das Video hier in Zeitlupe läuft und man im Video für die Zeitlupe
so in etwa 2 s erhält. 92,7 m sind auf jeden Fall viel zu groß. Nach Video
stürzt der PKW in der Nähe der Brücke ab, obwohl man am Ende
des Videos keine Absturzstelle erkennt. Man könnte hier mit
Reibung argumen- tieren. Man sieht ja, dass
der PKW seine Flugrichtung ändert und abkippt. Möglicherweise ist die Anfangsgeschwindigkeit aber
immer noch zu groß. Nehmen wir mal für w = 30 m an, dann ergäbe sich
folgende Rechnung für v0 :
Sieht nach einer zu geringen Geschwindigkeit aus.
Die Reibung spielt anscheinend doch eine große Rolle. Man erkennt, dass Berechnungen in der Schule „ohne
Reibung“ manchmal nicht sehr sinnvoll sind. − Sprung von der Karlsbrücke (schwer) Im Film rettet Vin Diesel die Menschheit, indem er
sich auf das Tragflächenboot Ahab mit einem Fallschirm schießt. Vielleicht geht es auch einfacher, indem er sich
mit einem Motorrad von der Karlsbrücke aus, auf das Boot befördert (gemäß der bekannten Bond- Aufgabe
von Leifi). Vin Diesel kann ja auf jeden Fall
mit einer Motorcross- maschine gut umgehen (siehe Drogenkartellszene; Sprung über eine
Scheune, siehe 3. Gehen wir davon aus, er darf ausnahmsweise die
Karlsbrücke be- fahren (Yelena
darf im Film ja auch mit dem Chevrolet Pontiac GTO die Fußgängerbrücke befahren). Die Situation soll in etwa folgendermaßen aussehen:
Motorcross Maschine und Ahab befinden sich beide gleichzeitig
mittig unter bzw. über der Brüstung der Karlsbrücke. Ahab hat
eine konstante Geschwindigkeit von ungefähr 10 m/s Dies ergibt sich aus der
Vorbei- fahrt an einem Häuserblock, wobei Ahab für 30 m
ungefähr 3 s be- nötigt. Man kann es auch aus der Parasailing-Szene ableiten. Beim Parasailing werden zwischen
25 km/h und 50 km/h mit einem Motor- boot gefahren. Wir
liegen dann mit 36 km/h ziemlich in der Mitte dieser Werte. Aufgabenstellung: Vin soll unter den obigen Startbedingungen mit einer Motorcross Maschine genau auf Ahab landen. Welche Geschwindigkeit muss das Motorrad dann aufweisen? Die Karlsbrücke hat mit Brüstung un- gefähr eine Höhe von 14 m. Die Rampe soll
wieder einen Winkel von 15° aufweisen und mit der Brüstung abschließen, also wie in Aufgabe 1. Ahab selber habe eine Höhe von 1 m. Rechnung wieder ohne Reibung. Lösung: Übrigens bei einem Winkel von 15° und einer
Brüstungshöhe von 1 m, müsste die Rampe ca. 4 m lang sein, was bei einer
Breite der Brücke von 10 m durchaus möglich ist. Wir sind wieder beim schiefen Wurf. Was kennen wir?
Wir legen ein Koordinatensystem, wie üblich, in den
Absprungpunkt, also in 14 m Höhe. Ahab selber ist 1 m hoch. Also ist die y-Koordinate von Ahab immer bei −
13 m. Nennen wir die horizontale Bootstrecke xB und die horizontale Motor- crossstrecke xM ergibt sich zwischen den beiden Strecken
(s. Abb.) der Zusammenhang xM = xB / sin(45°) mit xB = 10
m/s ∙ t (gleichförmig). Schaut man in die Formeln, wird ein Vorgehen wie in der Bondaufgabe, bei der zunächst die Fallzeit bestimmt wird, extrem
schwierig, da in allen Formeln auch vM
= Geschwindigkeit des Motorrades enthalten ist. Man muss also ein Gleichungssystem mit zwei Unbekannten
lösen, welches nicht linear ist. Hier die Formeln:
Dies ist in dieser Form im normalen Schulunterricht nicht
möglich. Man müsste komplexe Programme, wie „mathematica“
bemühen. Wir können aber zur Abschätzung einmal den waagerechten
Wurf berechnen, um einen Eindruck zu gewinnen, wo die Fallzeit
und damit die Geschwindigkeit von Vin liegen könnte. Wir tun jetzt
also so, als ob Vin Diesel in 14 m Höhe einen waagerechten Wurf mit dem
Motorrad durchführt. Er ergibt sich:
Das Ergebnis ist äußerst interessant, weil es nämlich
zeigt, dass es vollkommen egal ist, wie groß die Fallzeit ist. Das
Ergebnis für vM ist immer gleich, weil es nur von vB
abhängt. Woran liegt das? Dies hängt mit der Anfangsbedingung zusammen, dass beide Körper zum
Zeit- punkt t = 0 s auf der gleichen Höhe sein sollen. Hinweis: Bei Leifi hat das Motorboot
einen Vorsprung von 10 m, ansonsten bräuchte man hier auch keine Zeit bestimmen, weil bei
gleicher Höhe, die x-Koordinate immer gleich wäre und somit vBond = vMotorboot
wäre. Bei unserer Aufgabe ergeben sich nur unterschiedliche Werte, weil die
Wegstrecke vom Motorrad sich mit dem Faktor 1/ sin(45°)
vergrößert und ein schiefer Wurf von α = 15° vorliegt. Somit erweist sich die Aufgabe bei genauem Hinsehen als
gar nicht so schwer, wie erst vermutet. Wenn schon vM immer gleich
14,641 m/s ist, könnte man jetzt damit die Fallzeit bestimmen. Wir brauchen von der t−Formel
nur den Teil mit dem „+“. Es gilt also:
Die Fallzeit beträgt also tFall
= 2,0595 s. Wer Lust hat, kann oben einsetzen und sieht, dass die
Gleichungen hiermit erfüllt sind. − Sprung über die Scheune (einfach) Zur Rekrutierung muss Vin einen Test in einem Drogencamp
bestehen. Hierbei springt er mit einer Motocross Maschine über
eine Scheune, indem er einen umgestürzten PKW als Rampe benutzt. Eine Motocross Maschine kann Geschwindigkeiten bis 100
km/h er- reichen, fährt aber im Gelände meist nicht schneller als
50 km/h. Die Rampe hat einen Neigungswinkel im Bereich von 40° bis
50°. Aufgabenstellung: Ist es mit einer Motocross Maschine möglich einen solche Sprung durchzuführen? Rechnung ohne Reibung, wie immer! Lösung: Die Scheune hat eine maximale Höhe von 10 m. Gibt man
noch etwas Reserve dazu, muss Vin mindestens 11 m Höhe erreichen.
Sie ist maximal 4-mal so breit wie hoch. Also muss Vin eine Länge
von 40 m überspringen. Wir rechnen mal ein bisschen nach, was so möglich ist. 1. Fall Vorgabe: v0 = 21 m/s ≈ 76 km/h = Mitte zwischen
50 km/h und 100 km/h α = 45° = Mitte zwischen 40° und 50°
Man sieht, bei diesen Vorgaben ist es kein Problem, die
Scheune zu überspringen. Für andere Vorgaben ( v = 21 m/s
bleibt) gilt: α = 40° → sh = 9,3 m, sW = 44,3 m α = 50° → sh = 13,2 m, sW = 44,3 m Resümee: Für v = 21 m/s gibt es für die Weite keine
Probleme, nur die Höhe ist bei kleinen Winkeln nicht gegeben. Man kann jetzt mal die Geschwindigkeiten bzw. Winkel vorgeben
und bestimmen, welcher Winkel bzw. Geschwindigkeit für sh
= 11 m nötig wäre. Die Formeln lauten dann:
Es ergibt sich dann. v0 = 14 m/s → kein α möglich v0 = 21 m/s → α = 45° v0 = 27 m/s → α = 34° α = 40° → v0 = 22,85 m/s ( ≈ 82
km/h) α = 45° → v0 = 20,78 m/s ( ≈ 75
km/h) α = 50° → v0 = 19,18 m/s ( ≈ 69
km/h) Dies zeigt, dass dieser Stunt für Vin Diesel wohl einer
der einfacheren war, da es fast immer möglich ist, die Höhe zu erreichen,
wenn die Geschwindigkeit genügend groß ist. Mögliche weitere Klausuraufgaben: Wer einmal etwas mit Reibung betrachten will, könnte sich z. Bsp. den Fallschirmsprung von Vin Diesel von der Foresthillbridge
ansehen. Im digitalen Physikbuch gibt es ein Kapitel mit Reibung im Zusammen- hang mit dem Skispringen. Man
kann sich auch ein Lernvideo
von mir bei youtube ansehen. Es gibt auch ein mathematisches
Kapitel zur Lösung der auftretenden Differentialgleichungen. Zum Fallschirmsprung liegen allerdings sehr schöne Quellen (s. dort) vor, so dass ich hierzu nichts an dieser Stelle schreibe. Zusatzmaterial:
- zur 1.
Klausuraufgabe: Sprung von der Foresthill Bridge - zur 2.
Klausuraufgabe: Sprung von der Karlsbrücke - zur 3. Kausuraufgabe.Sprung über die Scheune - zurück
zum Kapitel „Schiefer Wurf“ - zurück
zum Oberkapitel „Bewegungen“ |