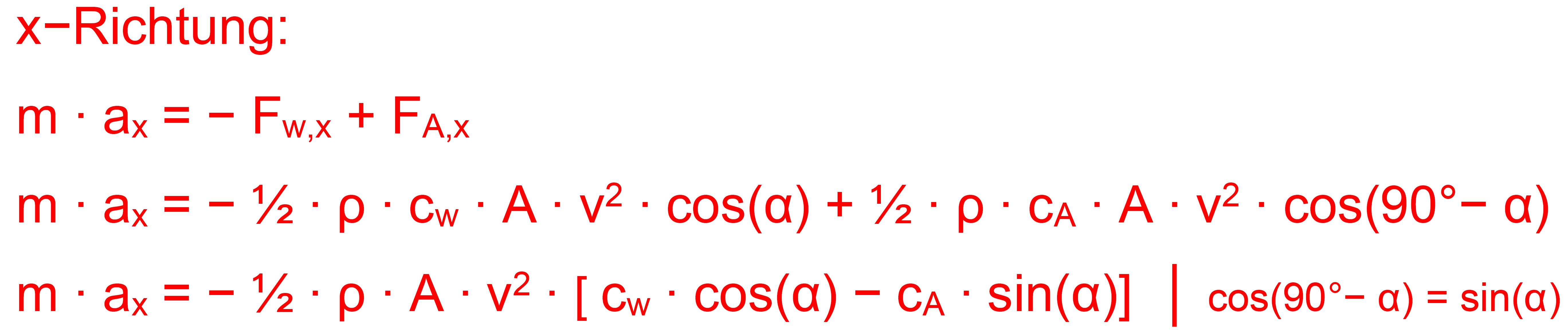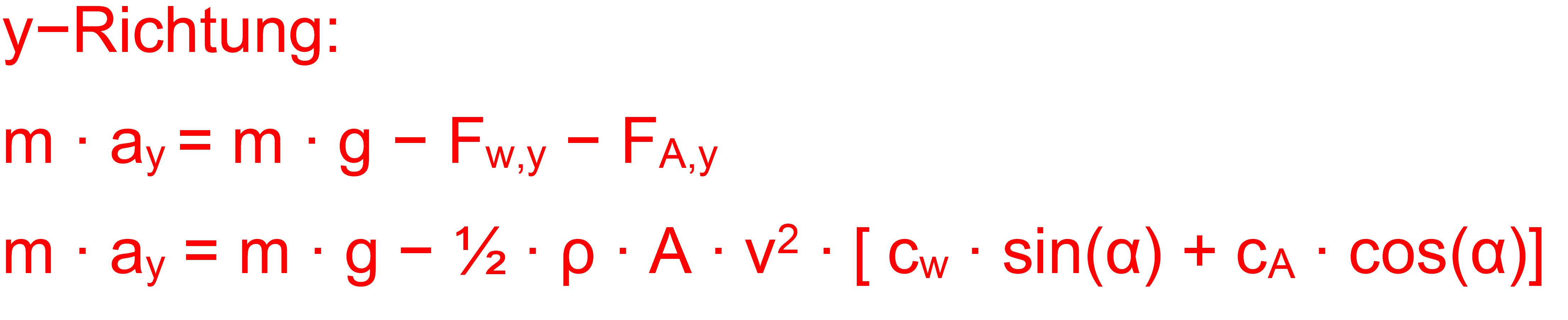|
Skispringen
- Extrateil Wir haben uns über eine Klausuraufgabe
schon einmal mit dem Skispringen beschäftigt. Dort musste man viele unrealistische Annahmen
machen, um die Aufgabe mit Mittel der Schulphysik rechnen zu können. Jetzt wollen wir uns die Verhältnisse noch einmal genauer
ansehen. 1. Teil:
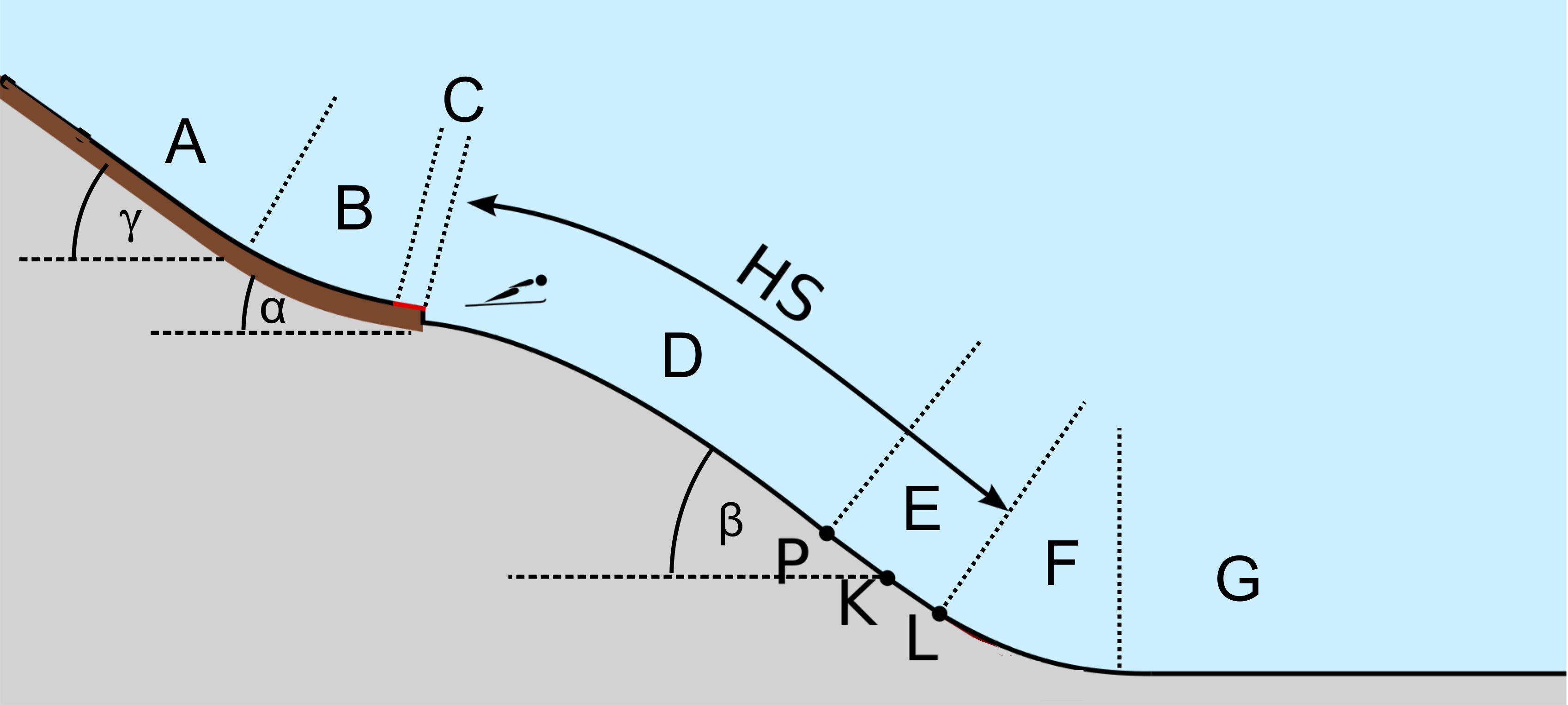
Zunächst zum Aussehen einer Skisprungschanzenanlage.
Quelle: https://de.wikipedia.org/wiki/Skisprungschanze#/media/Datei:Ski_jumping_hill_profile.svg leicht verändert !!! Man kann sieben Abschnitte unterscheiden, die durch die
Buchstaben A−G gekennzeichnet sind. Hinweis: Ich orientiere mich bei den Einteilungen an den
Unterlagen von Hans-Heini Gasser, dem Pionier im Skischanzenbau. ( s. Link 1 + 2 )) A: Der Anlauf bildet eine schiefe Ebene. Der Neigungswinkel
γ sollte einen Wert zwischen 30° bis 35° haben und maximal 37° betragen. B: Der Übergangsbogen stellt die allmähliche Verbindung
zwischen dem geradlinigen Anlauf und dem geradlinigen Schanzentisch C her.
Früher war dies häufig ein Kreisbogen. Bei neueren Schanzen soll es
eine Klothoide darstellen, wie dies z.B. bei Loopings in Achterbahnen
üblich ist. Ziel ist wohl, wie bei der Achterbahn, dass der Übergang zur
gekrümmten Form nicht zu abrupt passiert, so dass die g-Werte im Rahmen
bleiben. Diese werden mit maximal 1,7 angesetzt. Nach Gasser würde aber eine
Parabel dritten Grades (kubische Parabel) ausreichen (Link 2.)). C: Der Schanzentisch verläuft wieder geradlinig. Der Winkel
α bewegt sich in einem Bereich von 10°−11°. Die Tischlänge beträgt
zwischen 6 m und 8 m. D: Man spricht vom Vorbau des Aufsprungprofils.
Hier hat sich wohl eine kubische Parabel (s. „B“.) als Form bewährt. Ziel ist
es, dass der Abstand zwischen Springer und Aufsprunghang
nicht zu groß wird. E: Der Landebereich ist durch die Punkte P, K und L
gekennzeichnet. Am Punkt P beginnt der Landebereich. Dies ist der
„Wendepunkt“ des Profils, d.h. ab hier geht das Profil von der nach unten offenen Parabel in einen nach oben offenen Kreisbogen über. Es liegt ein
recht großer Radius für den Kreis vor. Die Belastung beim Aufsprung soll
möglichst 1,8 g nicht überschreiten. Die Winkel bei P, K und L
unterscheiden sich nicht wesentlich. Bei P ist natürlich der größte Winkel mit
max. 37°, bei K ca. 35° und bei L um die 32°. F: Der Übergangsbogen zwischen Landebereich und
Auslaufbereich G wird durch eine quadratische Parabel dargestellt. G: Der Auslauf kann verschiedene Formen aufweisen. Es soll
allerdings ein möglichst fließender Übergang zwischen L und G
stattfinden. Zu den Punkten P, K und L: - Der Punkt P (s.o.) entspricht dem „Wendepunkt“, also dem
Übergang von nach unten offener kubischer Parabel zu dem nach oben
offenen Kreisbogen. - Der Punkt L wird auch Hillsize-Punkt
genannt. Hier ist der Landebereich zu Ende. Eigentlich soll kein Springer weiter als L
springen, weil es dann zu gefährlich wird. Die Erfahrung zeigt, dass dieser Punkt
häufig doch übersprungen wird. Für die Hangneigung hat der frühere
Renndirektor Walter Hofer als Richtwerte 32° (für Normalschanzen), 31°
(für Groß-schanzen) und 27°− 28° (für Flugschanzen) angegeben (Link 3 hierzu). - Der Punkt K ist eigentlich der wichtigste Punkt. Er heißt
auch Konstruktions- punkt, weil nach ihm zum großen Teil das Profil der Schanze
konstruiert wird. Die Lage ist im Rahmen der Erfahrung offensichtlich frei
wählbar. Man soll auf dem Punkt sicher landen können. Es sind Neigungswinkel
β um 35° vor- gesehen. Viele Werte einer Schanze bestimmen sich aus der
Lage von K und dem Verhältnis h/n ( h = Vertikale Entfernung zwischen
Absprung und Punkt K, n = horizontale Entfernung zwischen Absprung und Punkt
K). Zitat aus Link 1 S.9: „Die Ausgangswerte einer Schanze sind die Weite w zum Punkt
K und die Steilheit, ausgedrückt durch das Verhältnis h/n.“ „Die beiden Größen w und h/n sind an sich weitgehend frei
wählbar. Die jahrzehntelange Erfahrung mit Schanzen aller
Größenordnungen hat eine Einschränkung dieser Freiheit geboten“. Im Folgenden sieht man einmal ein paar Werte wichtiger
Größen für einige Schanzen an (Link 4 hierzu).
Hinweis: die letzten vier Schanzen
gehören zur Vierschanzentournee 2.Teil: Reale Physik beim Skispringen (Quelle 1) Bei der Klausuraufgabe
zum Skispringen musste man viele Einschränkungen machen, um die Aufgabe überhaupt rechnen zu können, vor
allem wurde auf Reibung verzichtet. Beim Skispringen kommt es aber vor
allem auf Reibung an, sonst wäre nicht der V−Stil
erfunden worden, wobei die Anströmfläche stark vergrößert wird. 2.1. Verhältnisse beim Anlauf Der Skispringer bewegt sich beim Anlauf auf dem
Schanzentisch in einer Anlaufspur. Diese Anlaufspur entspricht einer schiefen
Ebene. Die be- schleunigende Kraft (ohne Reibung) ist also die
Hangabtriebskraft mit FH
= m ∙ g ∙ sin(α). Da der Springer in die Anlaufspur gedrückt wird, findet
also auf jeden Fall Gleitreibung statt, die allerdings durch das Material der
Spur (Schnee, Eis usw.) möglichst gering gehalten
werden soll. Außerdem ergibt sich ein Luftwiderstand, denn der Springer bewegt sich natürlich
nicht im Vakuum. Für die Gleitreibung ergibt sich die Formel FR = µ ∙ FN , wobei FN die Normalkraft ist, d.h. die Kraft, die senkrecht (also
normal) auf die Spur drückt. µ ist der Gleitreibungskoeffizient.
Im ersten Teil des Anlaufes (schiefe
Ebene) wirkt als Normalkraft die Komponente der Gewichtskraft, die senkrecht zur Spur zeigt.
Im Kapitel „Schiefe
Ebene“ erhält man dafür die Formel FN = m ∙ g ∙ cos(α), mit α dem Neigungswinkel der schiefen Ebene, also in unserem Fall
γ (schiefe Ebene am Start) oder α (Neigung des Tisches) bzw. etwas dazwischen
(kubische Parabel). Sobald die kubische Parabel erreicht wird, kommt noch die
Zentrifugalkraft zu der Normalkraft der schiefen Ebene hinzu. Wenn man die
kubische Parabel als „Kreisbogen“ ansieht, erhält man für die Kraft
die Formel FZ = m ∙ v2/r. Für den Luftwiderstand gilt die Formel FW = ½ ∙ ρ ∙ cw ∙ A ∙ v2 mit ρ = Luftdichte, A = Größe der Stirnfläche =
Querschnittsfläche, die von vorne angeströmt wird, v = Geschwindigkeit des
Springers (windstill) = Relativ- geschwindigkeit zwischen Springer und Außenluft = Anströmge- schwindigkeit, cw
= Strömungswiderstandskoeffizient (hängt stark von der Form ab).
Die Widerstandskräfte wirken alle entgegen der
Bewegungsrichtung, d.h. sie vermindern die Beschleunigung. Da die Luftreibung von v
„quadratisch“ abhängt, erfolgt eine starke Vergrößerung des
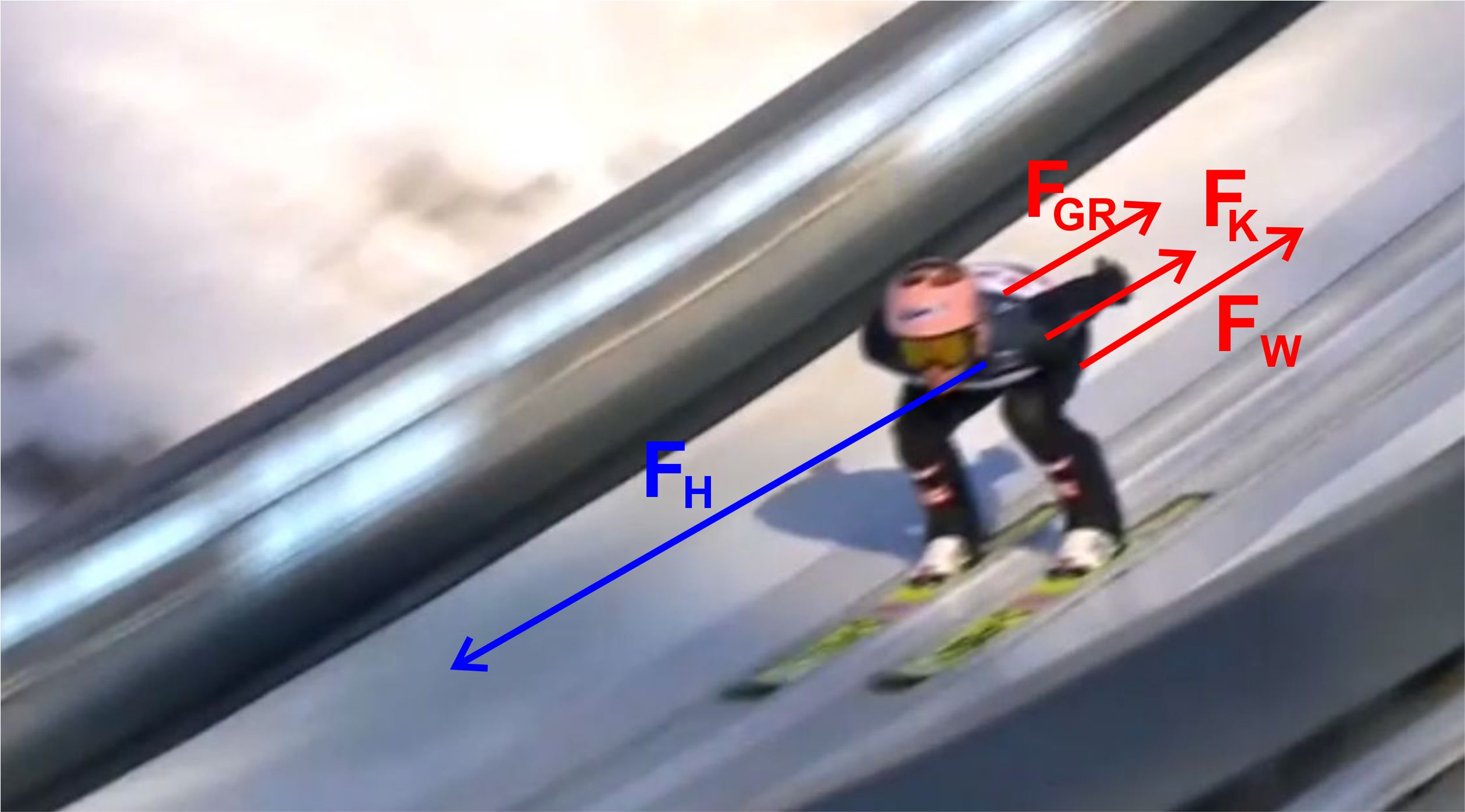
Luftwiderstandes mit der Geschwindigkeit. Die Richtungen der Kräfte kann man sich an folgender
Abbildung noch einmal ansehen:
FH =
m ∙ g ∙ sin(α) = Hangabtriebskraft (sorgt für die
Beschleunigung) FGR = µ ∙ m ∙
g ∙ cos(α) = Gleitreibung durch die schiefe Ebene FK = µ ∙ m ∙
v2/r = Gleitreibung durch Kurvenverlauf FW = ½ ∙
ρ ∙ cw ∙ A ∙ v2
= Luftwiderstand Wir fassen zusammen: Die beschleunigende Kraft F = m ∙ a (Grundgleichung
der Mechanik) ergibt sich aus der Hangabtriebskraft, der Widerstandskräfte durch
Gleitreibung und Luftreibung. Es gilt also:
Wenn man diese Gleichung nach v auflösen will, ist das
nicht ohne weiteres möglich. Es muss eine Differentialgleichung gelöst werden,
da a = v‘ ist. 2.2. Verhältnisse im Flug Es
liegen ähnliche Verhältnisse wie beim schiefen
Wurf vor, nur das in diesem Fall die Luftreibung berücksichtigt werden
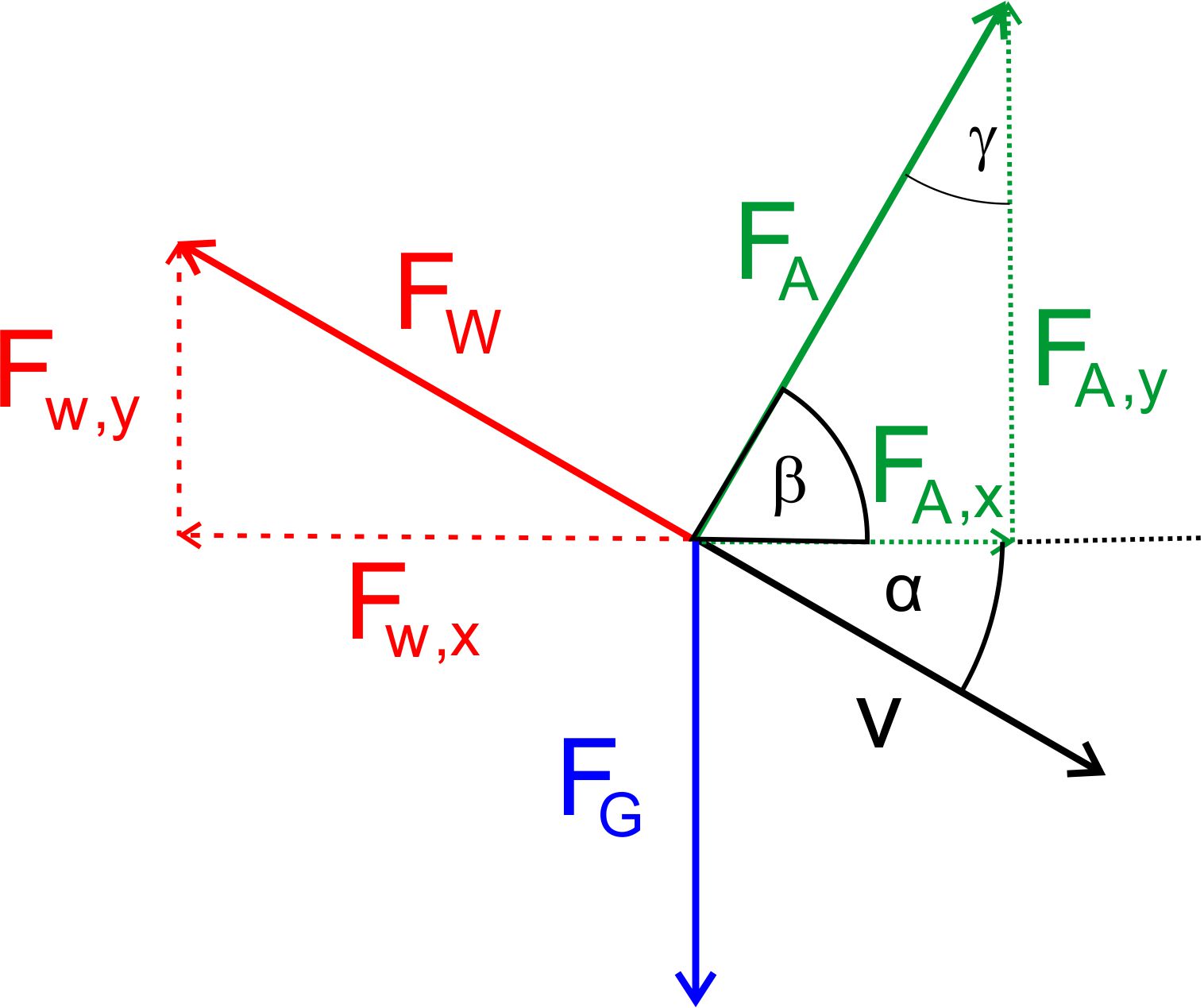
muss. Man zerlegt, wie beim
schiefen Wurf in eine Komponente in x-Richtung (Horizontale) und in eine
Komponente in y-Richtung (Vertikale). x- und y-Koordinate be- ziehen
sich auf ein Koordinatensystem mit dem Ursprung im Absprung- punkt. x-Richtung: Es liegt
wegen der Reibung leider keine gleichförmige Bewegung vor. Die
Anfangsgeschwindigkeit vx,0 in der Horizontalen wird sich immer
mehr verringern aufgrund des bremsenden Luftwiderstandes. Neben
dem Luftwiderstand, der entgegengesetzt zur Geschwindigkeits- richtung
wirkt, kommt jetzt noch eine dynamische Auftriebskraft zum Tragen. Diese
spielt beim Anlauf „wohl“ kaum eine Rolle, weil die Luft in der Hocke nicht
senkrecht zur Geschwindigkeitsrichtung angreifen kann. (s. Link Nr.1). Wenn ein
Körper („Platte“) aber schräg zur Bewegungsrichtung in der Luft
steht, gibt es neben dem Widerstand auch
einen Auftrieb. Der Auftrieb wirkt
genau senkrecht zur Bewegungsrichtung. Für den Auftrieb gilt die Formel FA = ½ ∙ ρ ∙ cA ∙ A ∙ v2
,
also ähnlich wie FW nur mit einem anderen Faktor, nämlich cA = Auftriebsbeiwert. y-Richtung: Auch
hier wirken Komponenten des Luftwiderstandes und der dynamischen Auftriebskraft,
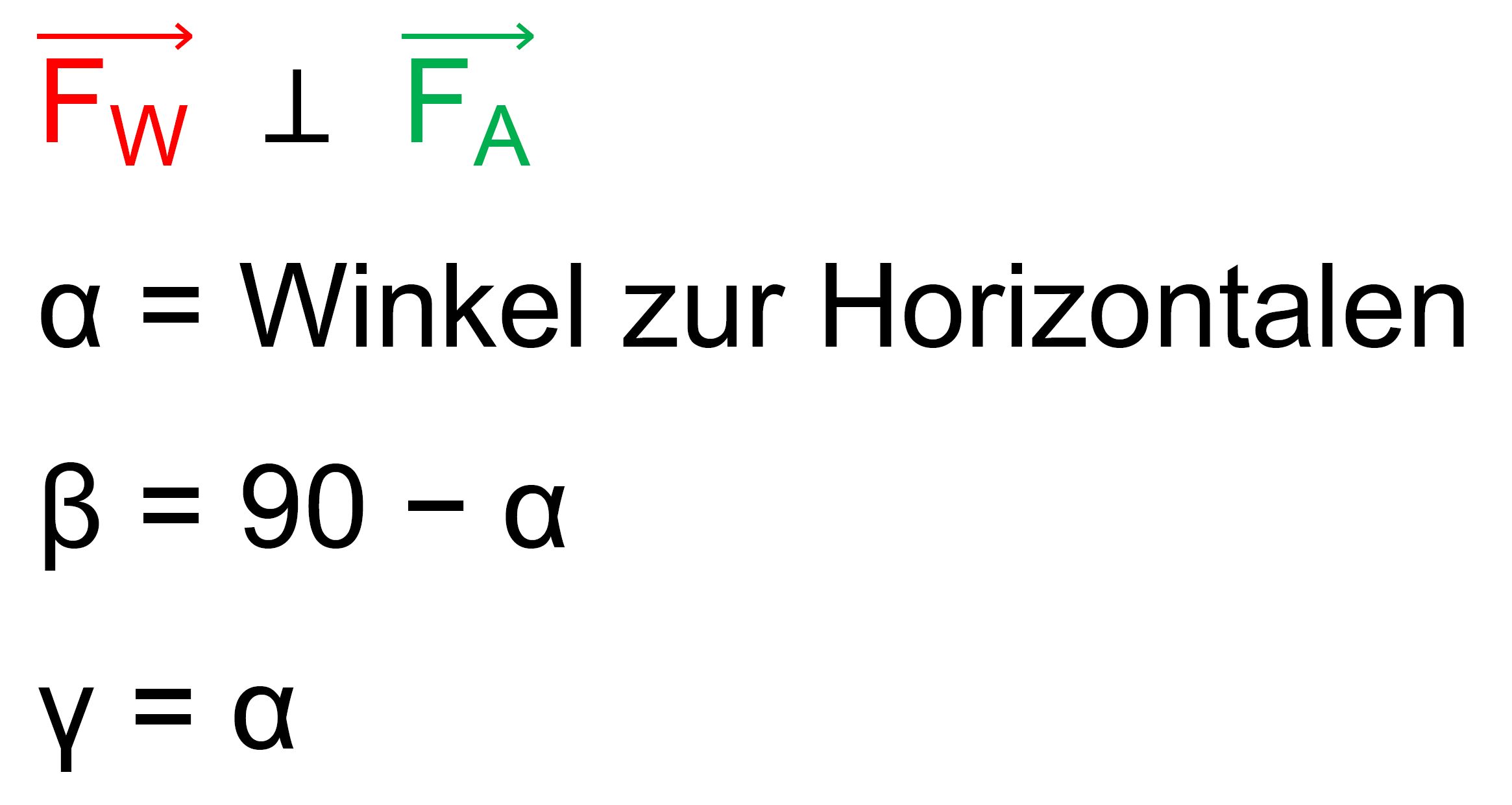
allerdings zusätzlich noch die Gewichtskraft. Wir betrachten die Verhältnisse einmal an einer Abbildung.
Somit ergibt sich jetzt.
Es sind wiederum Differentialgleichungen zu lösen. 1.Hinweis: Zur Lösung der Differentialgleichungen gibt es einen Extrateil. 2.Hinweis: Man findet in der Literatur häufig statt „Luftwiderstand“ den englischen Begriff „drag“ und statt „Auftrieb“ den
Begriff „lift“. 3.Hinweis. Wer etwas zum Absprung wissen will, sollte sich
die Quellen „zum Skisprung 1.)+2.)“ ansehen. Trotz intensiver Recherche ist es extrem schwierig Werte
für cW und cA zu finden, obwohl diese Werte natürlich den Ablauf des
Skispringens stark beeinflussen. Für folgende Beispielaufgaben ist versucht worden, die
Größen gut zu schätzen. Daher sind die Aufgaben sicherlich mit Fehlern
behaftet. Hinweis: Wenn jemand Werte für cW und cA
beim Skispringen kennen sollte, biite ich darum, mich über E-Mail zu informieren (Hinweise auf der Startseite der homepage).
Ich würde dann die Beispielaufgaben umarbeiten. Beispielaufgaben
Quellen und Links:
- reale Physik beim Skispringen - Lösung der DGL für die schiefe Ebene im Realfall -
|