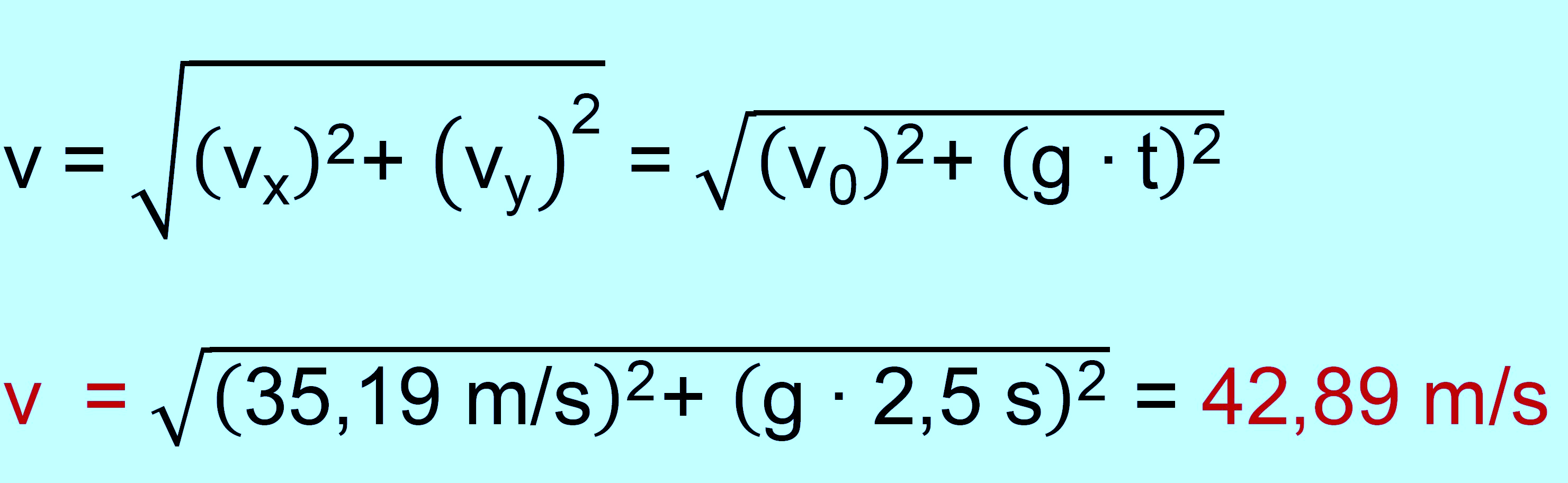|
Waagerechter
Wurf – Klausuraufgaben 1. Klausuraufgabe:
Skispringen (mittel) Im Folgenden soll ein Skispringen auf der Mühlenkopfschanze in
Willingen betrachtet werden. Von der Mühlenkopfschanze wird dazu
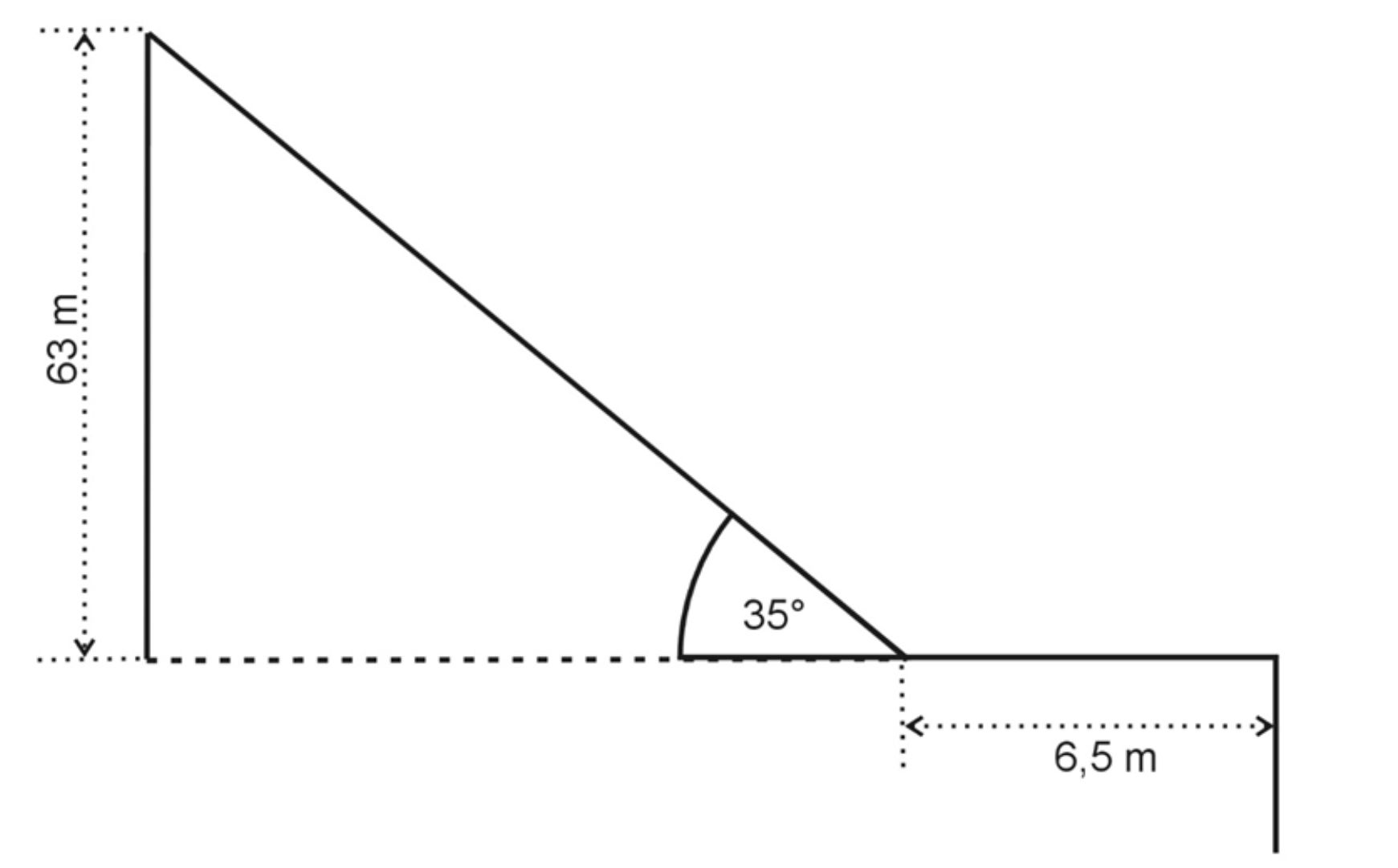
folgendes verein- fachtes Profil angenommen (s. Abb.). Die Schanze besteht
zunächst aus einer schiefen Ebene mit einem Neigungswinkel von 35°
(Anlauf). Hieran schließt sich eine waagerechte Ebene der Länge 6,5 m an
(Schanzentisch). Der Skispringer wird idealisiert als Massepunkt (ohne
Ausdehnung) angesehen, der reibungsfrei direkt auf der Anlaufebene
herunterrutscht.
a.) Ein Skispringer mit einer Masse von 65 kg startet
aus der Ruhe in einer Höhe von 63 m über dem Schanzentisch. Begründen Sie, welche
Bewegung der Skispringer ausübt? Berechnen Sie die Beschleunigung des
Skispringers. Bestimmen Sie die Zeit, die der Skispringer braucht, um bis
zum Schanzen- tisch zu gelangen. b.) Leiten Sie her, welche Geschwindigkeit er auf dem
Schanzentisch aufweist. [
Zur Kontrolle: 35,19 m/s ]. In den offiziellen Unterlagen zur Schanze wird eine
Endgeschwindigkeit von 26 m/s angegeben. Erklären Sie, wie es zu dieser
geringeren Geschwindigkeit kommt. Der Skispringer verlässt jetzt mit einer Geschwindigkeit von
35,19 m/s den Schanzentisch. Die Bewegung soll weiterhin reibungsfrei
betrachtet werden. Der Absprungpunkt soll der Ursprung eines Koordinatensystems
sein, im dem der Sprung im Folgenden betrachtet wird. c.) Berechnen Sie die Koordinaten des Punktes im
Koordinatensystem, in dem sich der Springer 2,5 s nach dem Absprung befindet. Welche Gesamtgeschwindigkeit weist er hier auf? d.) Die größte Skischanze der Welt steht in Vikersund
(Norwegen). Der Konstruktionspunkt (K-Punkt) liegt hier 100m unterhalb des
Schanzentisches. Ein Skispringer hat bei reibungsfreiem Flug
dort eine Geschwindigkeit von 53,5 m/s. Berechnen Sie die
Absprunggeschwindigkeit des Springers am Schanzentisch und seine Anfangshöhe beim
Start. Lösung: a.) Es liegt eine gleichmäßig beschleunigte Bewegung
vor, da die beschleunigende
Kraft konstant ist. Der Skispringer bewegt sich auf
einer schiefen
Ebene, d.h. die beschleunigende Kraft ist die Hangabtriebskraft. Für die
Hangabtriebskraft gilt: FH
= m ∙ g ∙ sin(α) = 65 kg ∙ 9,81 m/s2 ∙
sin(35°) = 365,7 N = konstant Da FH
konstant ist, gilt mit F = m ∙ a → a =
F/m = 365,7 N / 65 kg = 5,63 m/s2 Eine gleichmäßig beschleunigte Bewegung liegt vor. Man kann
die Formeln hierfür benutzen, also
b.) Die Geschwindigkeit v lässt sich mit v = a ∙ t = 5,63 m/s2 ∙ 6,25 s = 35,19 m/s
bestimmen. In den offiziellen Unterlagen liegt eine geringere
Geschwindigkeit vor, da sowohl Gleitreibung als auch Luftreibung nicht
berücksichtigt werden. Auch hier wird von einem reibungsfreien Bewegungsablauf
ausgegangen, was natürlich völlig unrealistisch ist, weil der Springer ja gerade ein gutes Luftpolster
ausbilden will, um lange in der Luft zu bleiben. Es wird also eine große Luftreibung (V-Stil
führt zu großer Fläche) erwünscht. Allerdings darf er auch nicht zu stark abgebremst werden,
damit er nicht zu schnell herunter- fällt. In manchen Aufgaben wird sogar von einer
gleichförmigen Bewegung ausgegangen. Wir
wollen die Formeln zum waagerechten Wurf üben, deshalb die un- realistische
Annahme. Nach
Voraussetzung soll der Ursprung des Koordinatensystems im Absprungpunkt
liegen. Hierauf beziehen sich also die nachfolgenden Angaben.
Der Absprungpunkt ist also der Abwurfpunkt für den waage- rechten Wurf. Es gilt: x−Koordinate = x−Richtung
= v0 ∙ t = 35,19 m/s ∙ 2,5 s = 88,0 m y−Koordinate = −
Strecke in y-Richtung nach unten = − ½ ∙ g ∙ t2 = −
½ ∙ g ∙ (2,5 s)2 = − 30,7
m Die Koordinaten lauten also ( 88,0 | −
30,7 ).
Die
Gesamtgeschwindigkeit bestimmt sich mit der Formel durch Einsetzen
Für
diese Aufgabe müssen Kenntnisse aus dem Bereich „Energie“ und „Energieerhaltungs- satz“
vorliegen. Die Landegeschwindigkeit ist viel zu hoch, da reibungsfrei
gerechnet wird.
Zusatzmaterial: Videos:
1.) − 3.) Mühlenkopfschanze: 1.) Sprung Geiger 2.) Helmkamera 3.) im
Sommer 4.) Vikersund: Weltrekord Stefan
Kraft
Links:
- Skispringen (reale Verhältnisse mit
Reibung) - Skispringen (Lösung der DGL) - zurück zum Kapitel „waagerechter Wurf“ - nächstes Kapitel „schiefer Wurf“ |