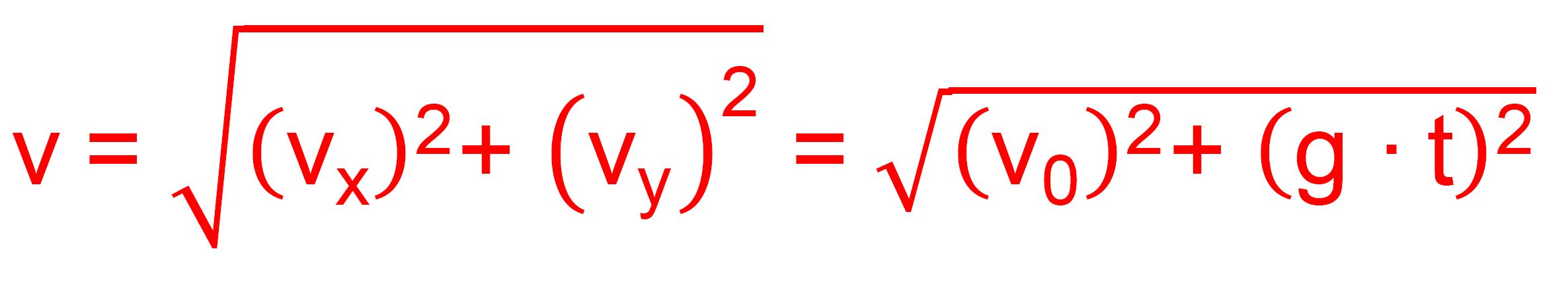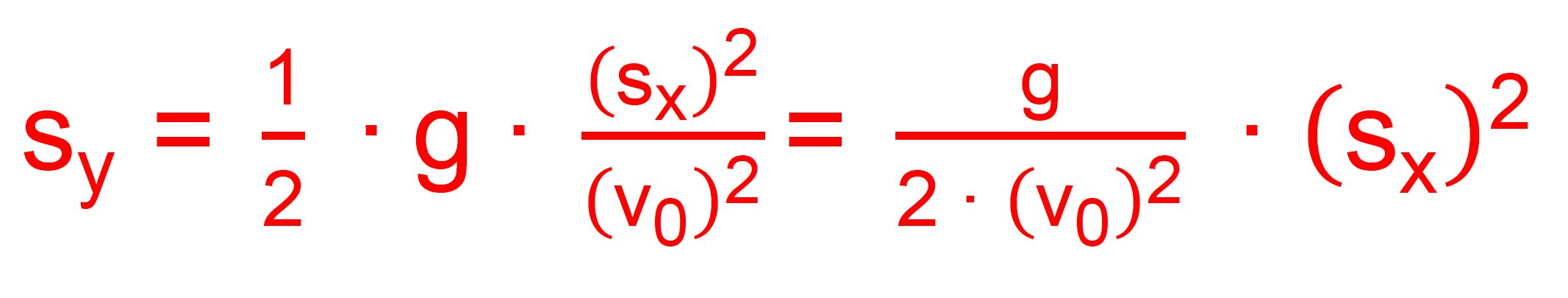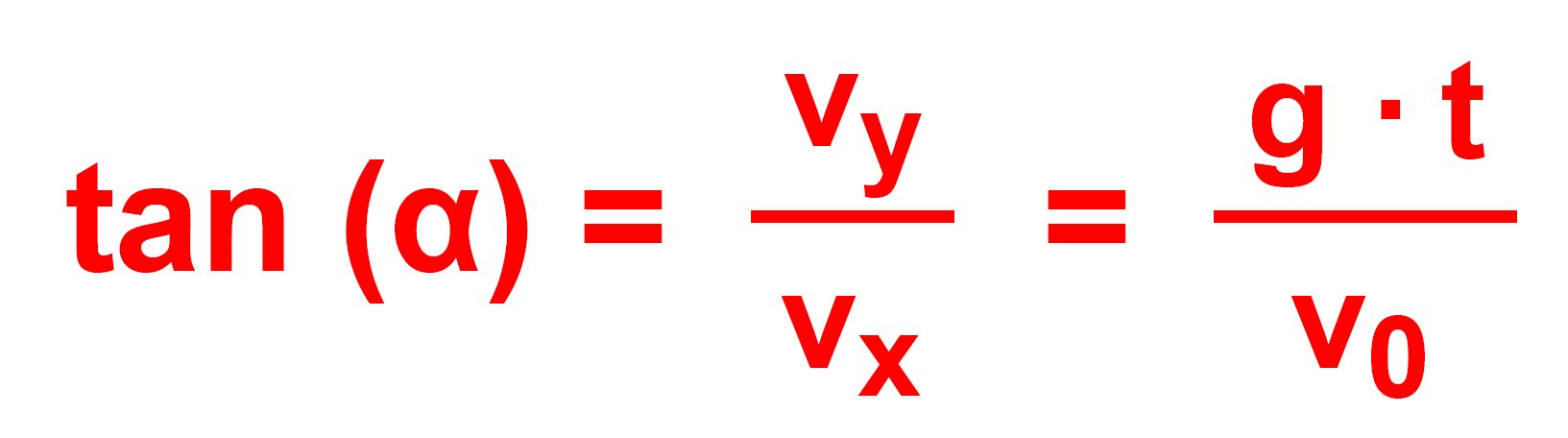|
Komplexe Bewegungen |
|||||||||
|
Waagerechter Wurf Ein waagerechter Wurf liegt vor, wenn der Körper horizontal (also parallel zur Erdoberfläche) abgeworfen wird. Wir untersuchen diese Bewegung zunächst wieder mit Videoanalyse. Hierzu wird folgendes Video ausgewertet. (beides auf eigenem
Computer speichern, Auswertung: s. Videoanalyse) Es wird in diesem
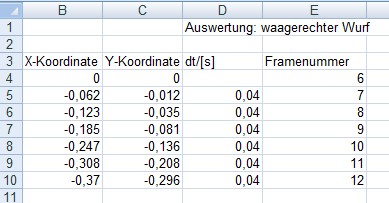
Fall die rote Kugel ausgewertet, die einen waage- rechten Wurf
durchführt. Man beginnt, wenn die Kugel den Bolzen verlässt (Frame 6)
und wertet sowohl die x- als auch die y-Koordinate Man erhält folgende
Exceltabelle:
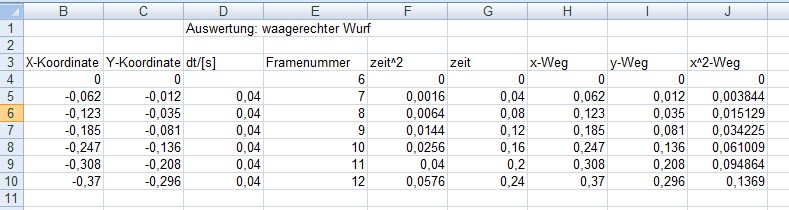
Bei einer weiteren
Bearbeitung in Excel ergibt sich folgende Tabelle:
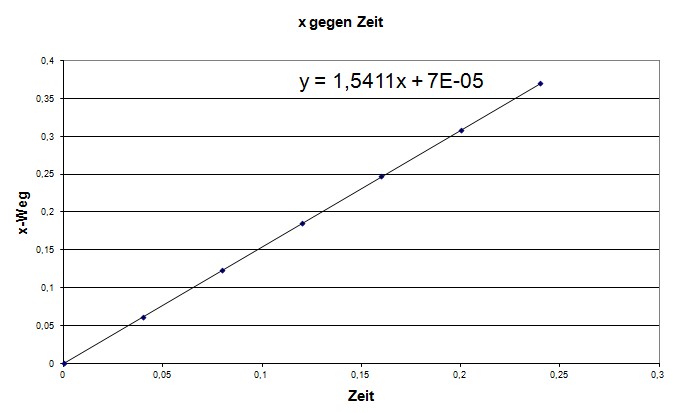
Lässt man die
zugehörigen Diagramme zeichnen, ergeben sich folgende Abbildungen:
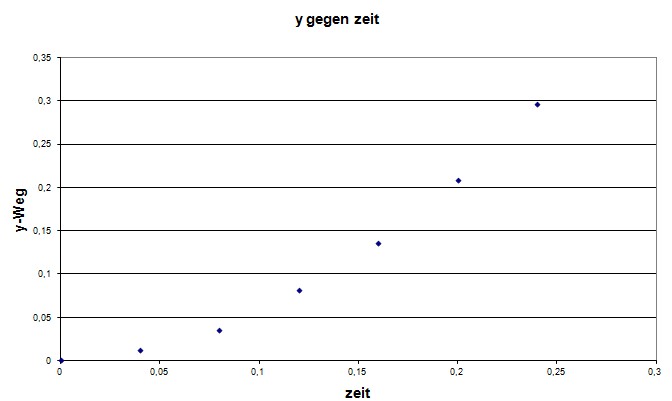
Man erkennt, dass es
eine Ursprungsgerade ergibt, d.h. es liegt eine gleichförmige Bewegung in der
Horizontalen vor (s.dort)
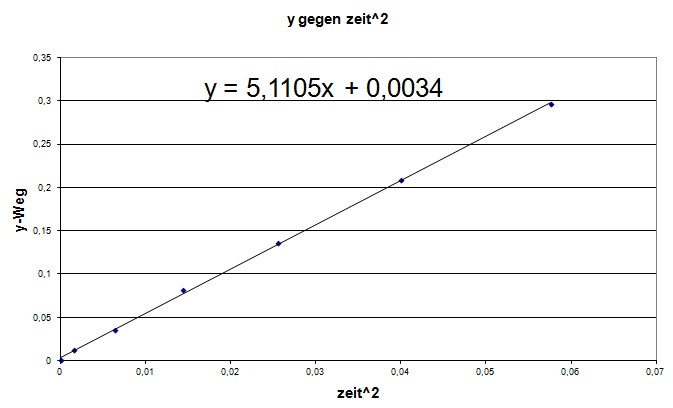
Hier ist erkennbar,
dass eine gleichmäßig beschleunigte Bewegung vorliegt (s.dort). Im Rahmen der Messgenauigkeit ergibt
sich ungefähr ein Wert von a = 10
m/s^2 für die Beschleunigung, d.h. es liegt wohl offensichtlich ein
freier Fall in der Vertikalen vor (s. dort).
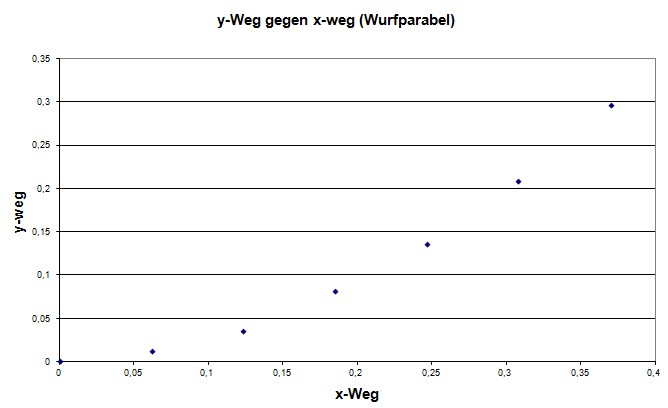
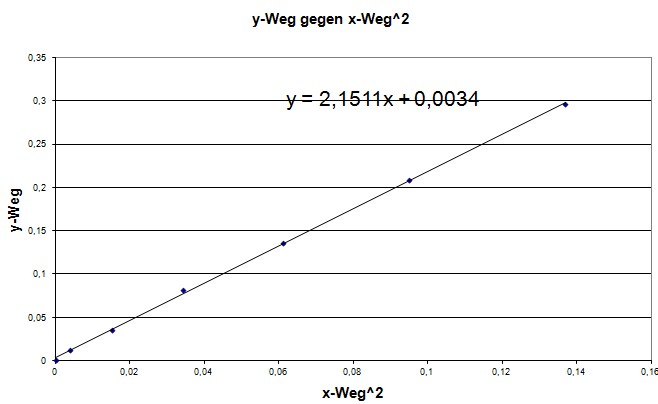
Auch der Zusammenhang
zwischen den Ortskoordinaten (die Bahn- kurve) ist
quadratisch. Deshalb spricht man bei der Bahnkurve von einer Wurfparabel. Superpositionsprinzip Beim waagerechten
Wurf kommt (wie man an der Auswertung sieht) das
Superpositionsprinzip zum Tragen. Dies bedeutet, dass
sich die komplexe Bewegung des waagerechten Wurfes aus einfachen
Bewegungen zusammensetzt, die sich ungestört überlagern. In diesem Fall ergibt
sich der waagerechte Wurf als eine Kombination zwischen einer
gleichförmigen Bewegung in der Horizontalen und einem freien Fall in
der Vertikalen. Den freien Fall kann man gut daran erkennen, dass sich
im Video die rote und die grüne Kugel immer in der gleichen Höhe
befinden. Bewegungsgleichungen Unter den
Bewegungsgleichungen versteht man die Abhängigkeit der jeweiligen
physikalischen Größen (Weg, Geschwindigkeit, Beschleuni- gung) in horizontaler
bzw. vertikaler Richtung von der Zeit. Er ergibt sich hierfür aufgrund der Superposition:
Für
die Gesamtgeschwindigkeit v ist eine vektorielle Addition der Einzelgeschwindigkeiten
notwendig. ( Zur vektoriellen
Addition findest man hier eine kleine Präsentation aus dem Internet: vektorielle Addition von Geschwindigkeiten
(Quelle:
Landesbildungsserver-Baden-Württemberg) . Es
ergibt sich dann für die Gesamtgeschwindigkeit (s.hierzu auch die Abbildung):
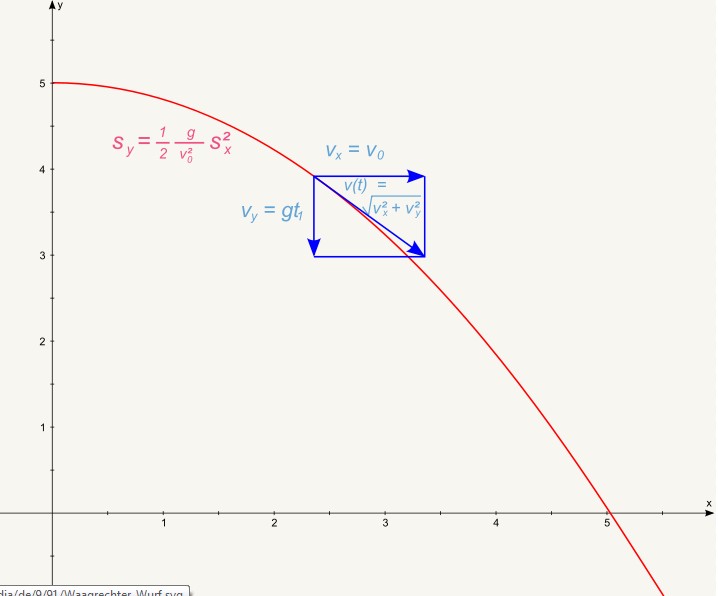
Quelle: Wikipedia (frei verfügbar) Herleitung der Formel für die Bahnkurve Die Herleitung der
Formel für die Bahnkurve (s. hierzu die Abbildung) geschieht, indem man
in die Formel für sy die nach t umgestellt Formel von sx einsetzt. Der Vorgang sieht dann also
folgendermaßen aus.
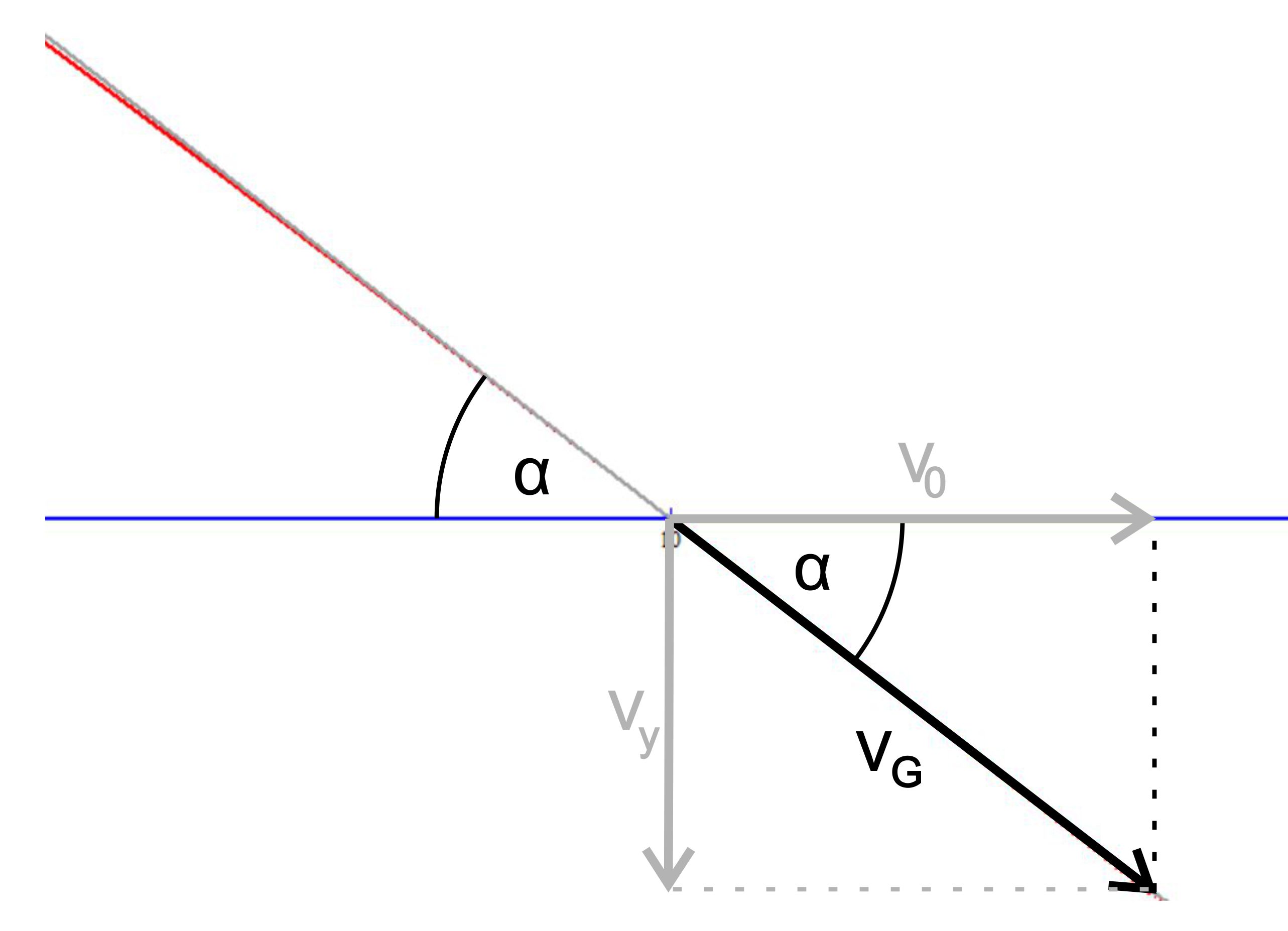
Herleitung der Formel für den Aufprallwinkel Der Aufprallwinkel
ist der Winkel mit dem der Körper auf dem Boden aufprallt, also ganz
genau der Winkel zwischen Erdboden und Bahn- kurve am
Aufprallpunkt. Die Richtung der Bahnkurve wird dabei durch die Richtung der
Tangenten an die Bahnkurve im Punkt angegeben und diese entspricht
somit der Richtung des Geschwindigkeitsvektors. Hierzu folgende
Abbildung:
blau: Erdboden; rot: Bahnkurve; schwarz: Tangente, α =
Aufprallwinkel, grau: Komponenten
|