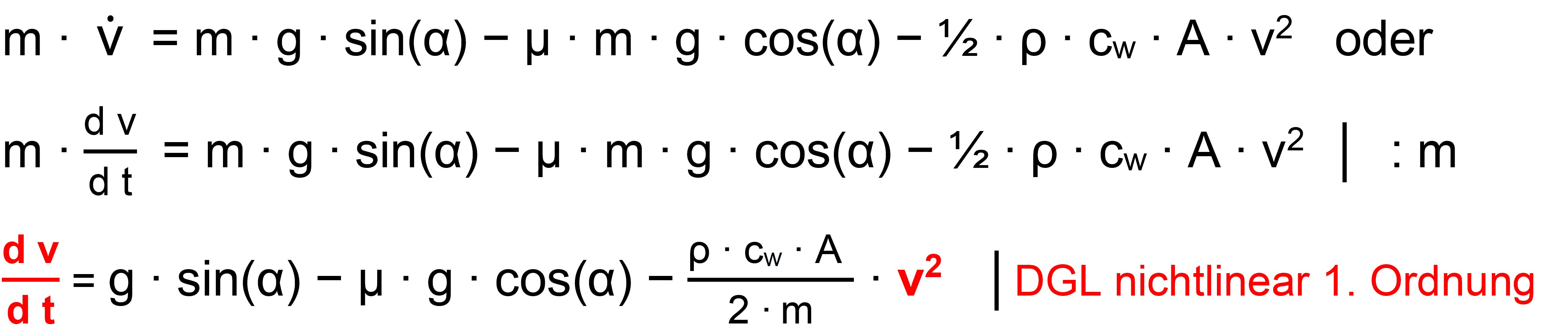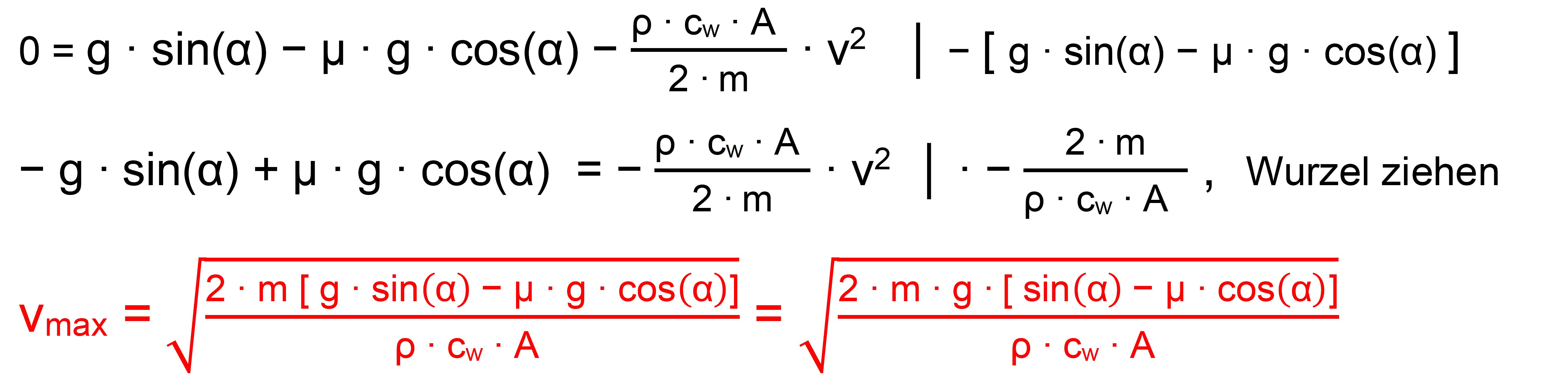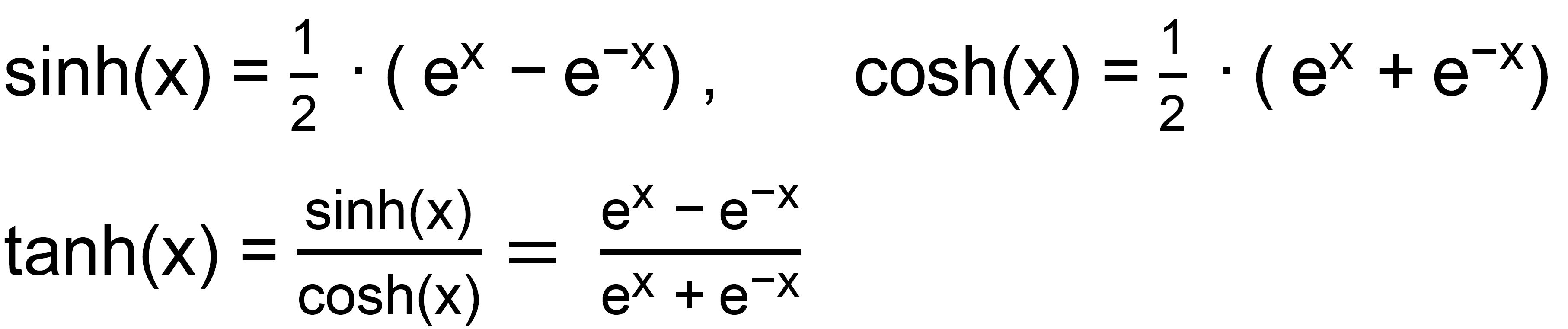|
Skispringen extra − Lösung der Differentialgleichung Im
Kapitel „Skispringen extra“ tauchen Gleichungen zu den auftretenden Kräften auf,
die eine Differentialgleichung (DGL)bilden. Wir wollen in diesem Kapitel
jetzt diese DGL lösen. Wir machen dies exemplarisch am Bespiel
der DGL für die Kräfte beim Anlauf auf der schiefen Ebene. Die
Kräftegleichung lautet hierfür: (s.
Skispringen extra) m ∙ a = m ∙ g ∙ sin(α) − µ ∙ m ∙
g ∙ cos(α) − ½ ∙ ρ ∙ cw
∙ A ∙ v2 Am
einfachsten ist es diese Gleichung für v zu lösen. Dann ergibt sich eine
relativ einfache DGL. Warum liegt überhaupt eine DGL vor? Man kann
a umschreiben, nämlich
Wenn man
dies für a in die Gleichung einsetzt, hat man eine Gleichung der
Originalfunktion v mit der Ableitung von v, also eine DGL. Es gilt
also:
Maximale Geschwindigkeit Bevor
wir jetzt die DGL lösen, wollen wir zunächst einmal eine Formel für die
Höchstgeschwindigkeit bestimmen, die man auf der schiefen Ebene
erreichen könnte. Warum gibt es überhaupt eine maximale Geschwindigkeit? Da der
Luftwiderstand von der Geschwindigkeit abhängt, wird dieser Wert
also immer größer, wenn eine Beschleunigung stattfindet. Irgend- wann
wird der Luftwiderstand zusammen mit der Gleitreibung also genau so groß wie
die Hangabtriebskraft sein. Dies würde bedeutet, dass auf der
rechten Seite keine Kraft mehr wirkt, also muss a = 0 m/s2 werden. Die
beschleunigte Bewegung ist in eine gleichförmige Bewegung überführt
worden. Dies passiert übrigens bei allen Bewegungen, bei denen
Luftreibung vorliegt. Die Bewegung muss allerdings lange genug stattfinden. Der
Ansatz für die Berechnung der maximalen Geschwindigkeit lautet also: m ∙
a = 0 bzw. FH = FR
+ FW (s. Skispringen extra) Es
ergibt sich dann:
Wir
setzen jetzt einmal die Werte aus „Skispringen
extra“ für Stefan Kraft
auf der Skischanze Vikersund (Monsterbakken) ein. Es galt dort ja: m = 60 kg, µ =0,05, A = 0,45 m2, ρ
= 1,2 kg/m3, γ = α = 36°, cW = 0,45, v = 22 m/s
Der maximale
Wert liegt sehr hoch und wird auf der Skischanze nie erreicht
werden. Beim Anlauf wird der Skispringer also die ganze Zeit beschleunigt. Lösung der Differentialgleichung Zunächst
einmal zu den Voraussetzungen (keine Schulmathematik) um die Rechenschritte
zu verstehen. Man muss sich in folgenden Inhalten
auskennen (vielleicht gibt es ja mal
ein digitales Mathematikbuch hierzu): - Hyperbelfunktionen
(Hyperbolicusfunktionen) :
- Umkehrfunktionen
der Hyperbelfunktionen (Areafunktionen)
- Wendet
man die Funktion f auf die Umkehrfunktion f−1 an, ergibt sich die
Identität oder in Formelschreibweise f (f−1(x)) = x -
Ableitungen und Integrale der obigen Funktionen, am wichtigsten
Lösungsweg:
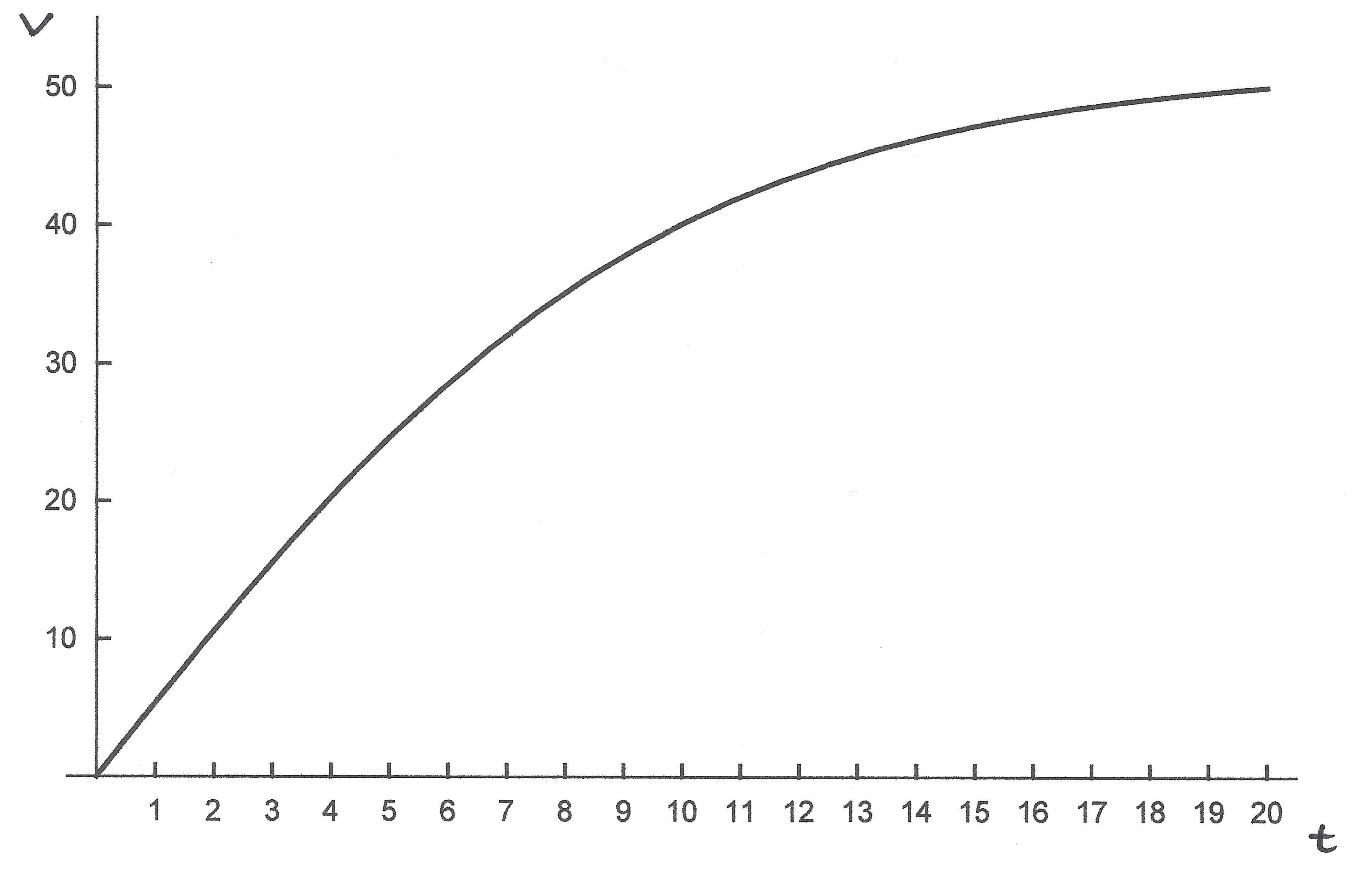
Der Graph
für die Werte von oben (Stefan Kraft) hat dann folgendes
Aussehen.
Man
erkennt die max. Geschwindigkeit bei v = 51,5 m/s, die erst nach ca.
20 s erreicht wird. Stefan Kraft braucht aber (s. Video) gerade
mal ca. 5 s bis zum Absprung und ca. 4 s auf der schiefen Ebene.
Dies würde nach der Abb. einer Geschwindigkeit von 88,6
km/h bzw. 73 km/h entsprechen. Dies
stimmt recht gut mit der Beispielaufgabe zum „Skispringen Extra“ überein.
Dies würde dafür sprechen, dass die Abschätzungen
gut gewählt sind. Zusatzmaterial:
Links und Quellen
- zur Beispielaufgabe „Skispringen“
ohne Reibung - Kapitel „zum Skispringen mit Reibung“ |