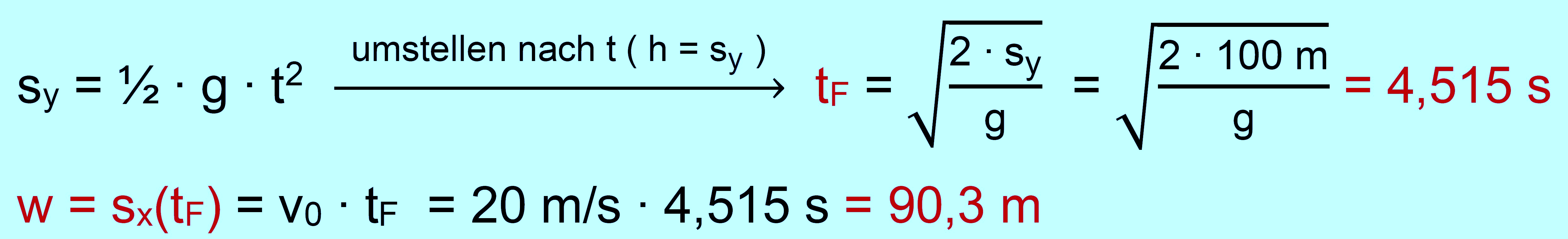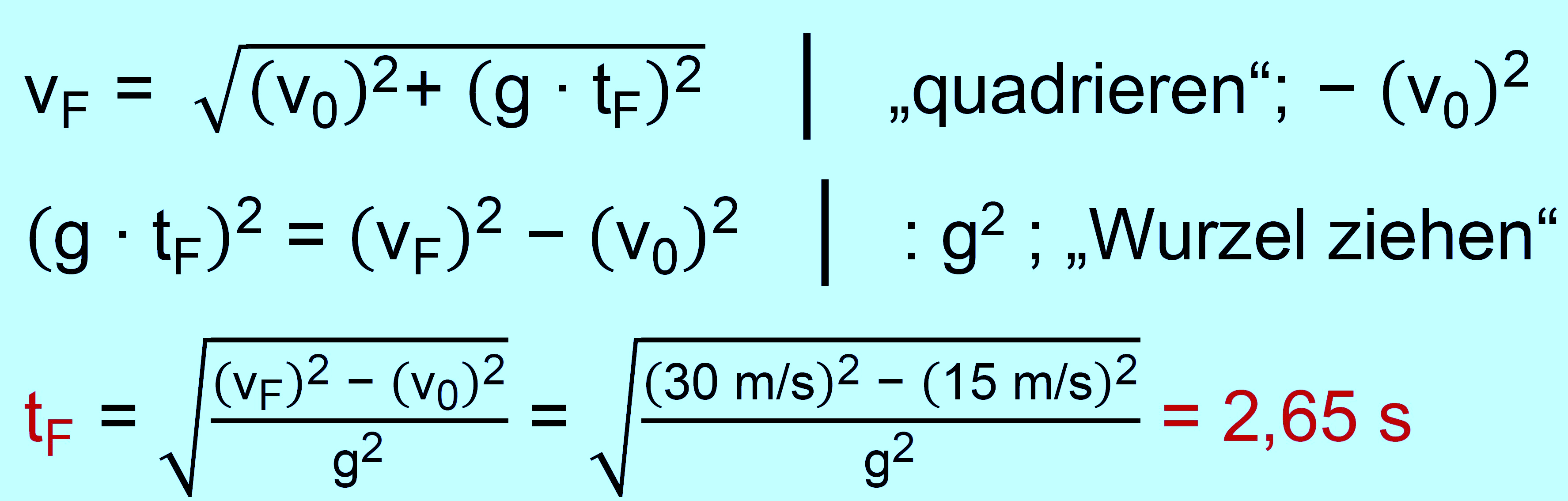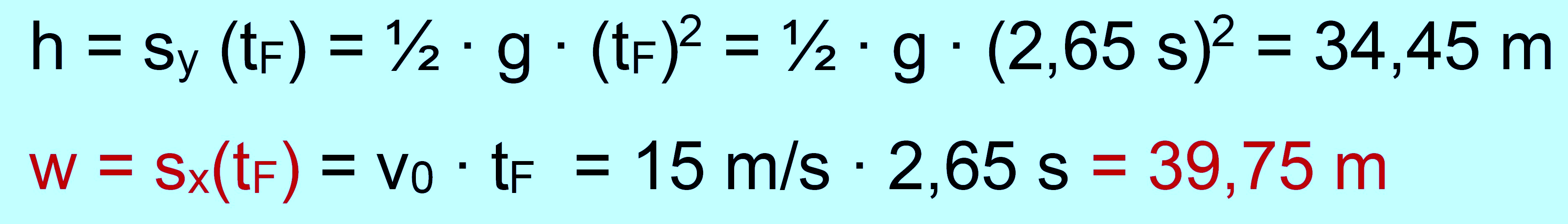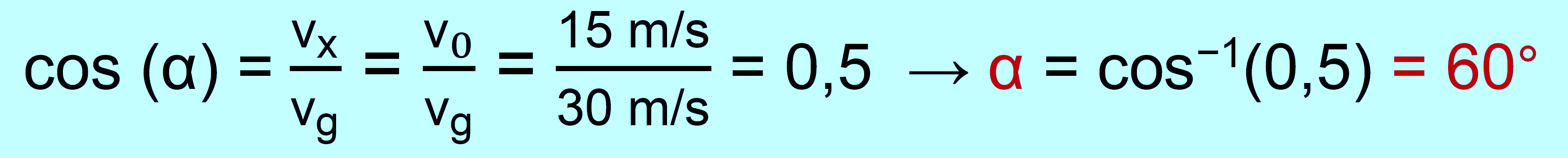|
Übungsaufgaben Übungsaufgabe
Nr.1 (leicht-mittel) Aus einer Höhe
von h= 100m wird ein Ball mit der Geschwindigkeit v0
= 20 m/s waagerecht abgeworfen. Wie weit
fliegt der Ball? Welche Aufprallgeschwindigkeit weist er auf? Lösung: gegeben: h = 100m; v0 = 20 m/s gesucht: w = maximale horizontale Strecke, vF = Aufprallgeschw. Es gibt keine Formel mit einem direkten Zusammenhang zwischen w und h. Man muss daher zunächst eine andere Größe bestimmen. In den Bewegungsgleichungen taucht immer die Zeit t auf. Also muss zunächst die Flugzeit tF bestimmt werden (s. Beispielaufgabe Nr.1).
Wenn man die Formel für tF in w einsetzt, erhält man eine Formel für w.
Aufprallgeschwindigkeit wie bei „Boris Becker“:
Übungsaufgabe Nr.2 (mittel-schwer) Ein Ball,
der mit der Anfangsgeschwindigkeit v0 = 15 m7s waagerecht abgeworfen
wird, kommt mit einer Aufprallgeschwindigkeit von vF
= 30 m/s auf dem Boden an. Berechnen
Sie die Abwurfhöhe, die Wurfweite und den Aufprall- winkel. Lösung: gegeben: v0 = 15 m/s; vF = 30 m/s gesucht: h; w; αF Vorgehen wie in ÜA 1, zunächst „tF“ bestimmen
Jetzt einfach nur einsetzen:
Statt tan(α) kann man besser cos(α) benutzen (s. waagerechter Wurf).
Übungsaufgabe Nr.3 (mittel) Nach einer
Flugzeit von tF = 7,5 s kommt ein Ball
mit dem Aufprall- winkel α
= 75° auf dem Boden auf. Berechnen
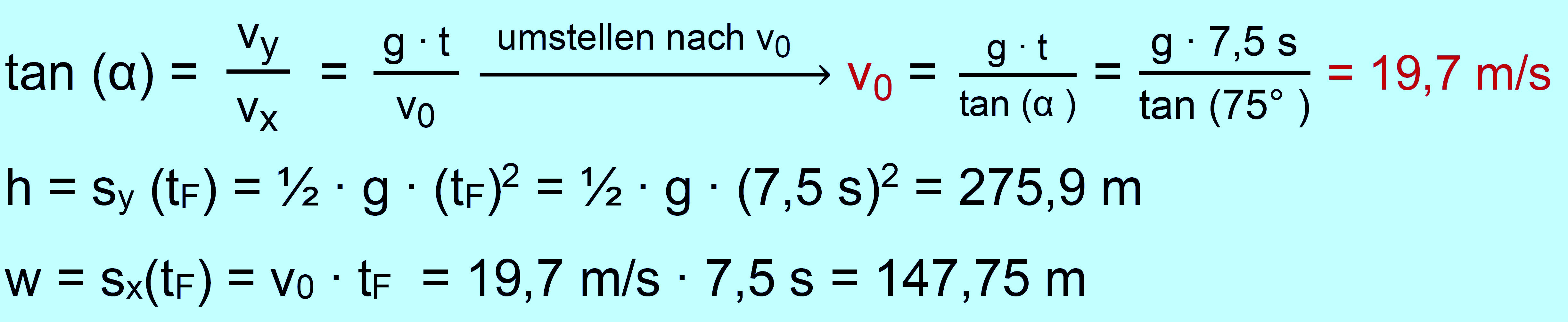
Sie die Anfangsgeschwindigkeit, die Abwurfhöhe und die Wurfweite. Lösung: gegeben: tF = 7,5 s; αF = 75°
Übungsaufgabe Nr.4 (sehr schwer) Ein Ball,
der aus einer Höhe von 100 m waagerecht abgeworfen wurde, geht auf
seiner Bahnkurve durch den Punkt ( 25 m | − 40 m ). Wie weit
fliegt der Ball? Lösung: gegeben: h = 100m; Bahnpunkt ( 25 | − 40 ) → sx = 25 , sy = − 40 - 40 ist eine Koordinate im Koordinatensystem (Ursprung = Abwurf) gesucht: w Es fehlen beide Größen v0 und tF. Beides muss zunächst ander- weitig berechnet werden.
- zurück zum Kapitel
„waagerechter Wurf“ - zurück zur Übersicht
„Bewegung“ |