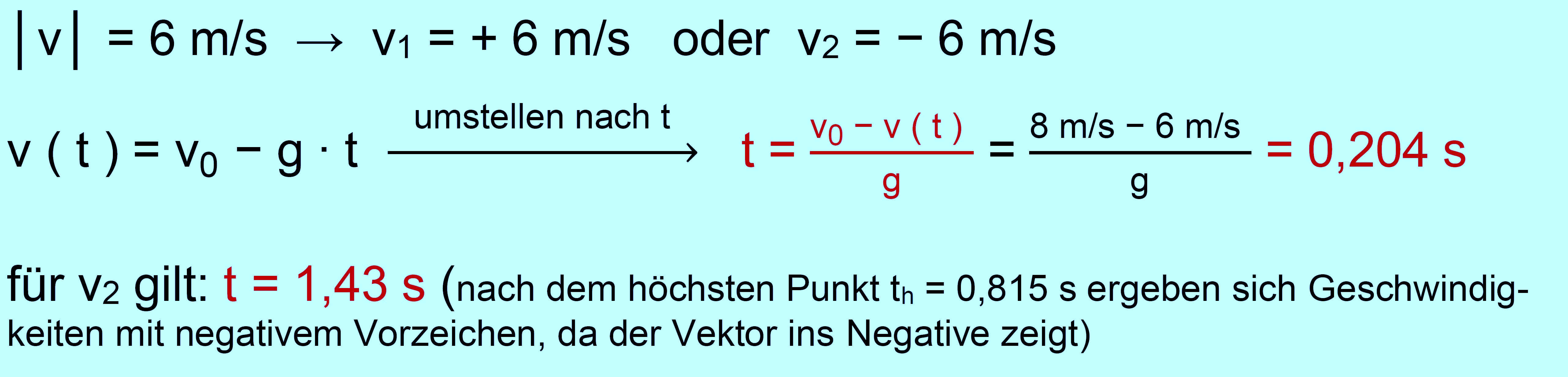
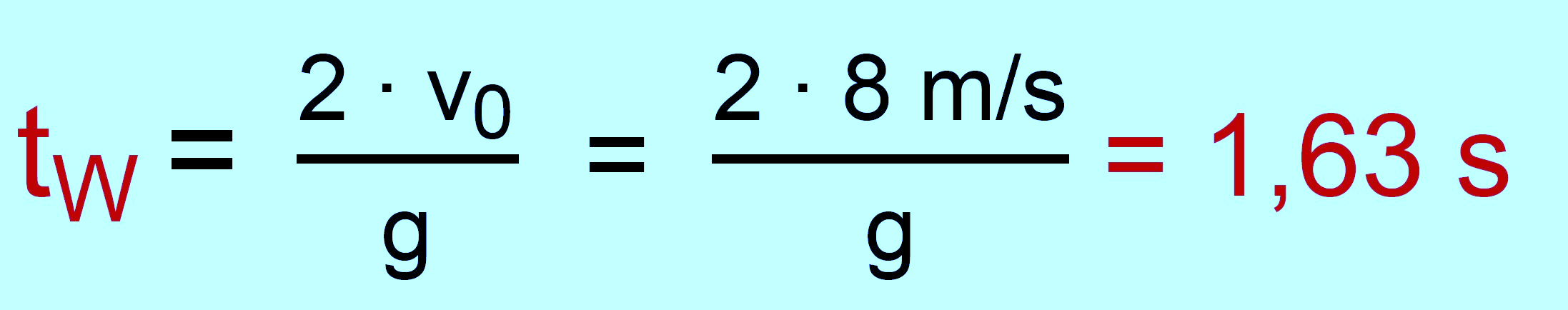Lotrechter Wurf oder Senkrechter Wurf

1.Fall: Wurf nach oben

Was versteht man unter einem lotrechten Wurf? Wenn man einen Gegen-

stand (z. Bsp. Ball) senkrecht zur Erdoberfläche nach oben wirft, übt man

einen lotrechten Wurf aus. Ein Beispiel wäre ein Volleyballspieler, der

einen Aufschlag von oben macht und dazu den Volleyball vor seinem

Körper senkrecht nach oben werfen muss. Dieser Aufschlag wird auch

Tennisaufschlag genannt,weil man ihn natürlich auch vom Tennis kennt.

Video zum Tennisaufschlag beim Beachvolleyball

Quelle: https://www.youtube.com/watch?v=nQSKxhpmkRY

https://commons.wikimedia.org/wiki/File:Flavia_Pennetta_at_the_2008_US_Open.jpg

Folgende Videos zeigen ebenfalls einen lotrechten Wurf nach oben und

könnten für eine Videoanalyse benutzt werden.

Quelle: https://www.youtube.com/watch?v=u0ttV_NQYZM

Quelle: https://youtu.be/dkb7Kl61wiI

Wir benutzen wieder (s. waagerechter Wurf) das Superpositionsprinzip,

welches uns bei komplexen Bewegungen immer gute Dienste leistet.

Welche einfachen Bewegungen überlagern sich aber beim lotrechten

Wurf?

Stellen wir uns vor, wir würden einen Ball im Weltraum (fern aller Massen)

mit der Geschwindigkeit v₀ versehen, würde er sich immer weiter mit

dieser Geschwindigkeit bewegen, also eine gleichförmige Bewegung

durchführen.

Kommt die Erde hinzu, tritt die Erdanziehung auf, die jetzt auf den Ball

einwirkt. Diese Kraft ist zum Erdmittelpunkt gerichtet. Bei einem lotrechten

Wurf nach oben, würde diese Kraft also die Bewegung nach oben „be-

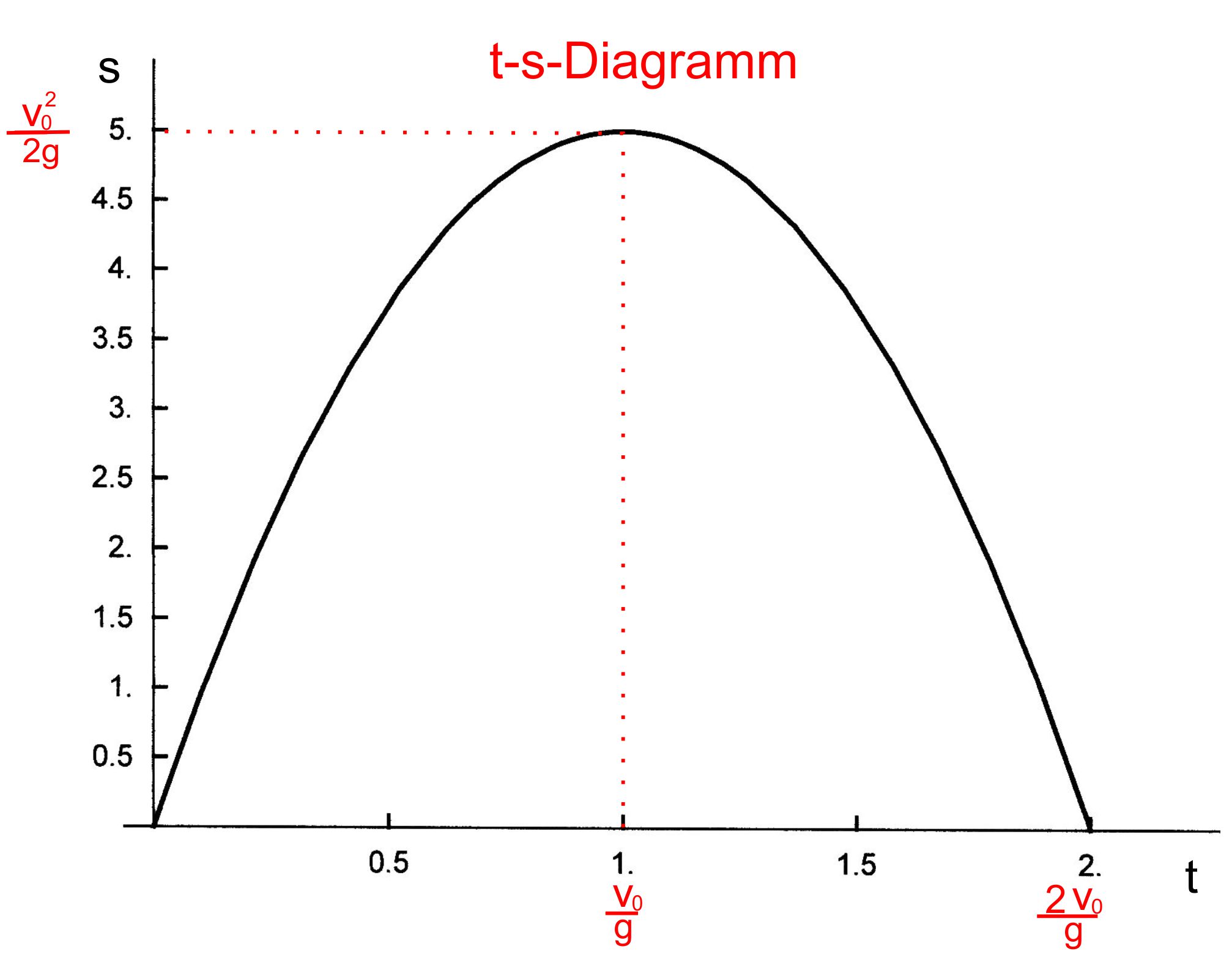
hindern“. Die Erdanziehung macht sich als freier Fall bemerkbar.

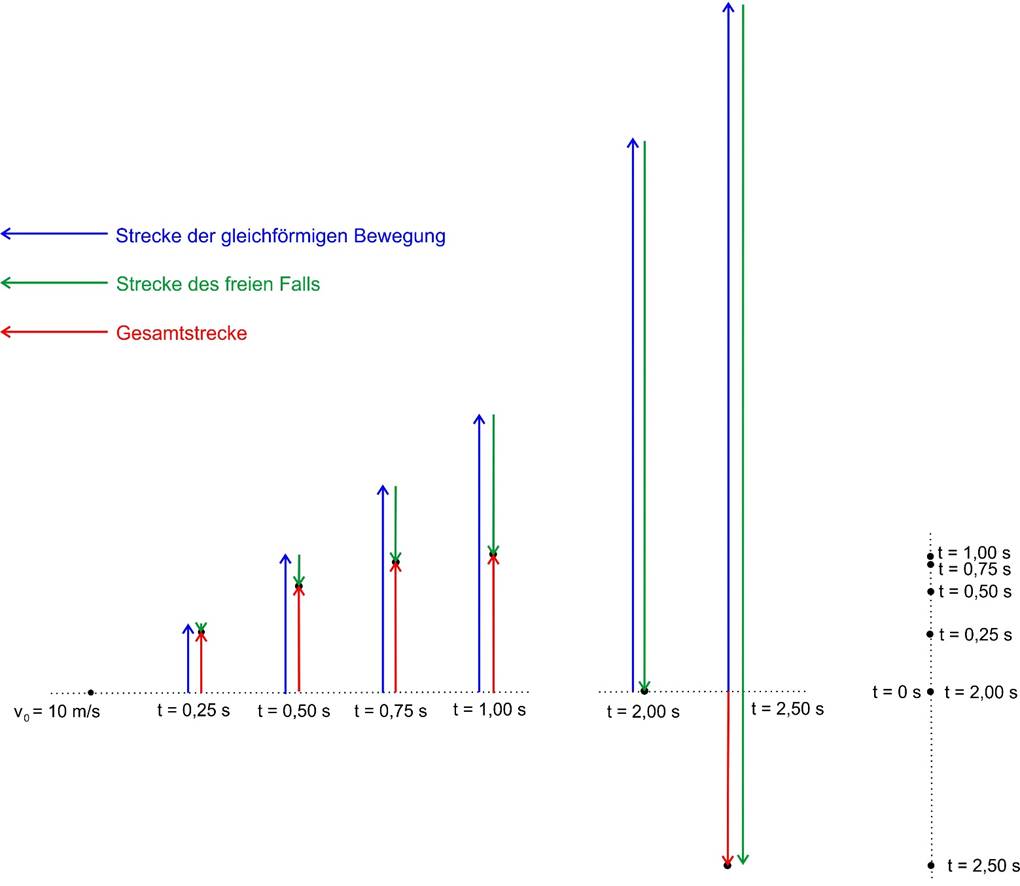
Es überlagern sich also eine gleichförmigen Bewegung nach oben mit

einem freien Fall nach unten.

Die folgende Abbildung soll dies noch einmal veranschaulichen.

Hierzu sind einmal der Streckenabschnitt durch die gleichförmige Bewe-

gung (blau) mit der Strecke durch den freien Fall (grün) kombiniert worden.

Es ergibt sich als Gesamtstrecke die rote Strecke. Links werden diese

Strecken zu verschiedenen Zeiten abgebildet, wobei die Anfangsge-

schwindigkeit v₀ = 10 m/s beträgt. Rechts sieht man die reale Bewegung

auf der lotrechten Linie.

Im Folgenden findet man eine sehr schöne Animation, die alle komplexen

Bewegungen betrachtet. Wir erhalten in dieser Animation einen lotrechten

Wurf, wenn man den Winkel +90° wählt.

Wenn man für Anfangsgeschwindigkeit 10 m/s wählt und die Ausgangshöhe bei 5 m einstellt, erhält man in etwa den Verlauf der obigen Abbildung. Am besten man benutzt immer die Zeitlupe.

Ändert man danach die Masse, erkennt man, dass sich der Geschwindigkeitsverlauf nicht ändert. Die Beschleunigung bleibt immer konstant, nämlich 9,81 m/s^2. Während des gesamten Wurfes ändert sich auch die Kraft nicht. Die Kraft hängt allerdings von der Masse ab.

Erklärung: In den Bewegungsgleichungen taucht nirgendwo die Masse auf, da der freie Fall ja von der Masse nicht abhängt.

Die wirkende Kraft ist die Gewichtskraft F = m*g. Diese hat keine Abhängigkeit von v.