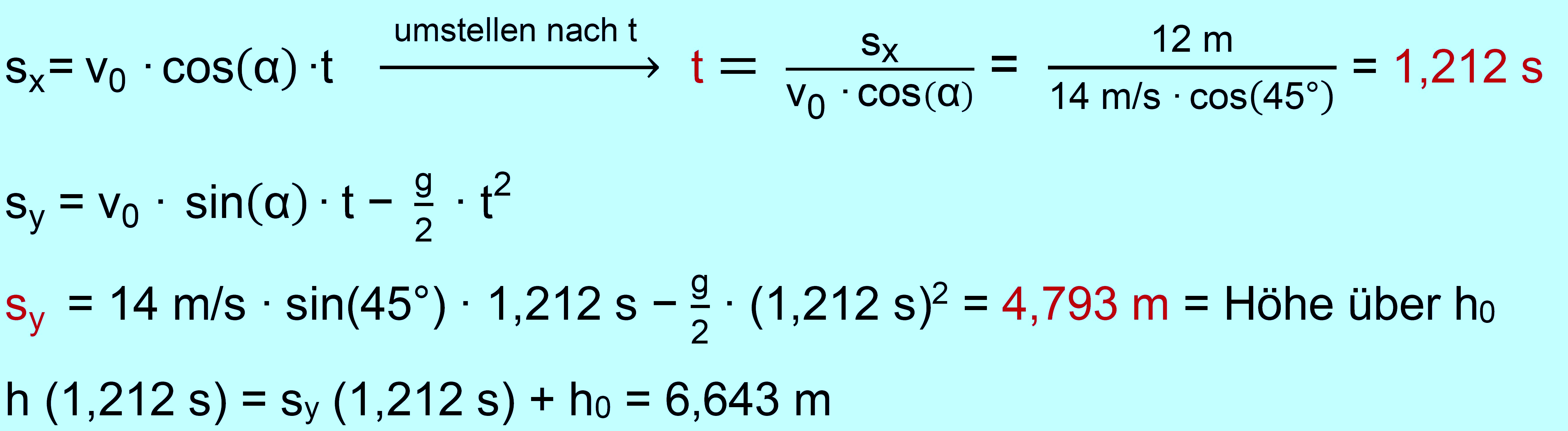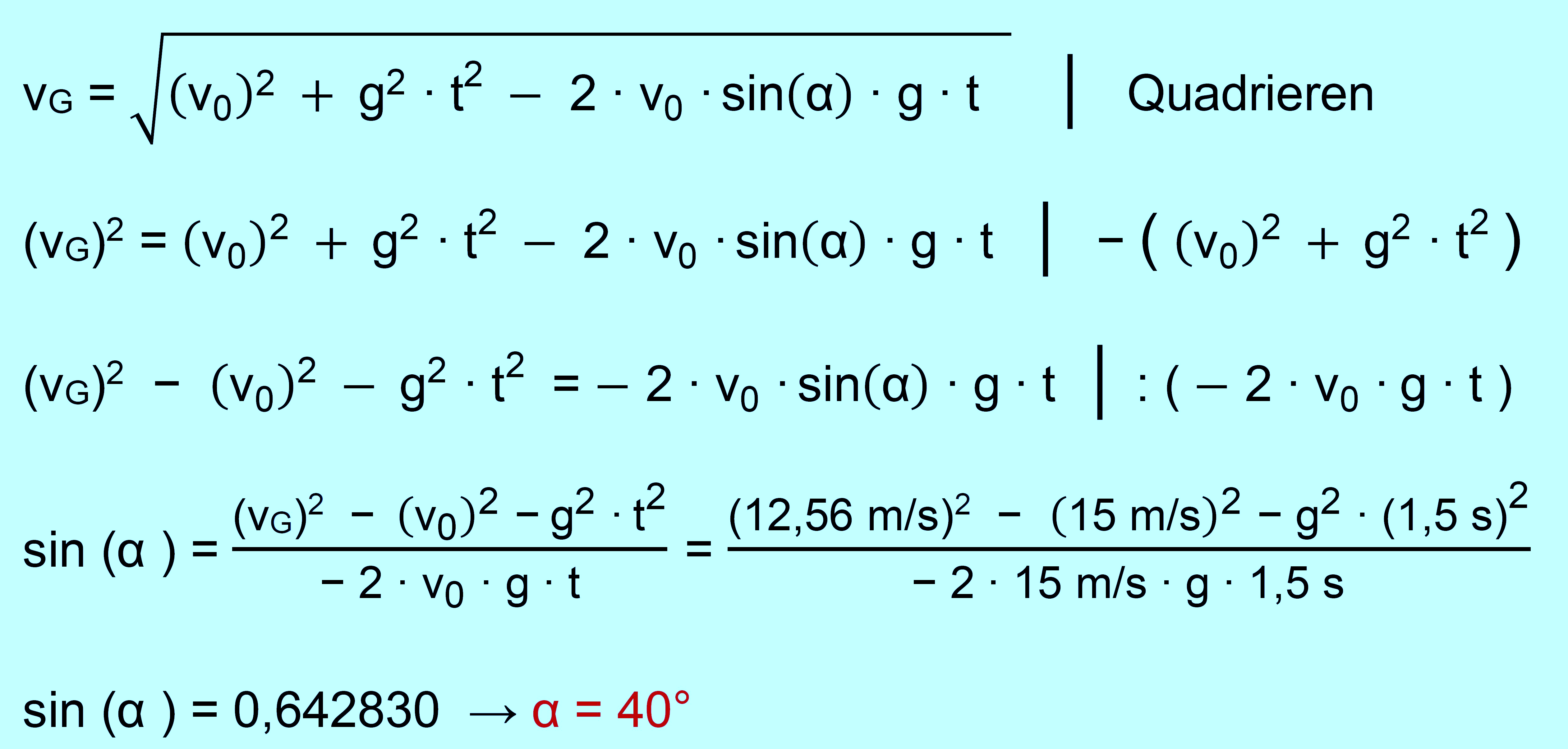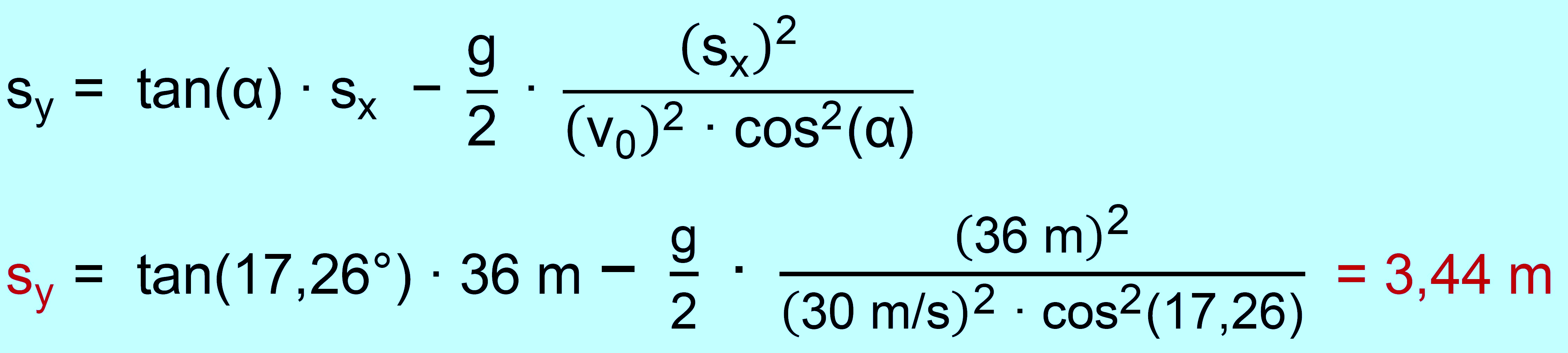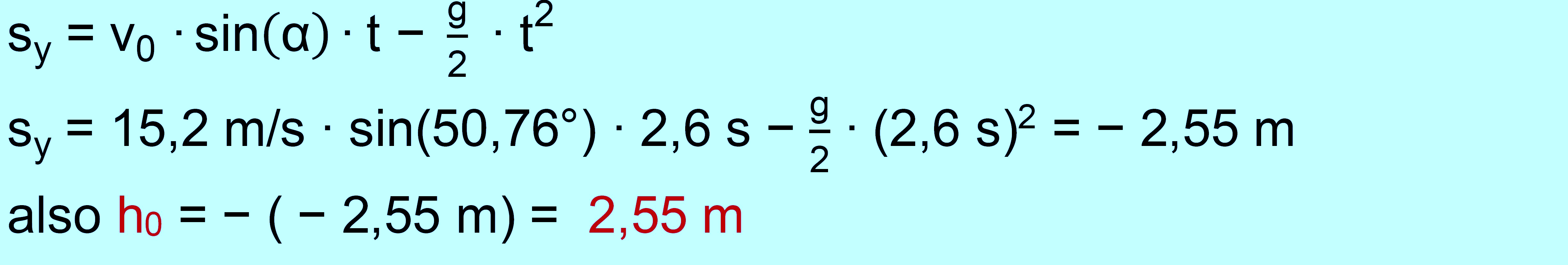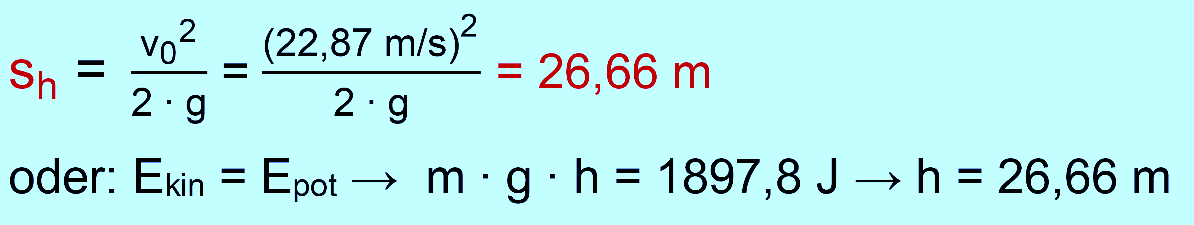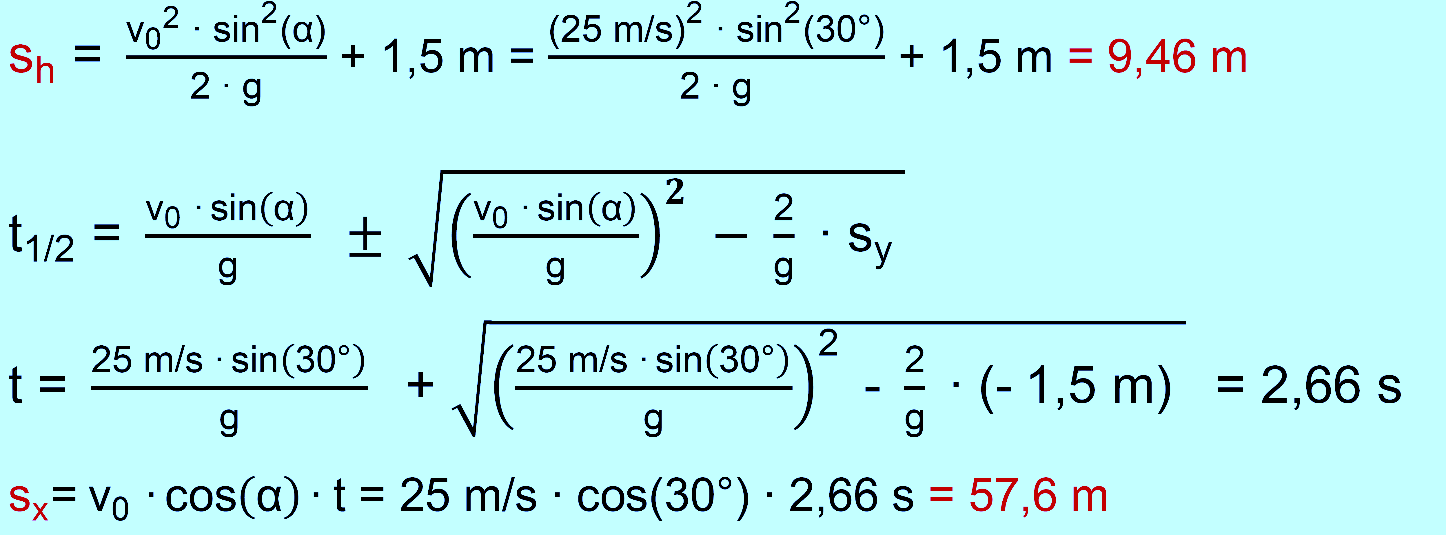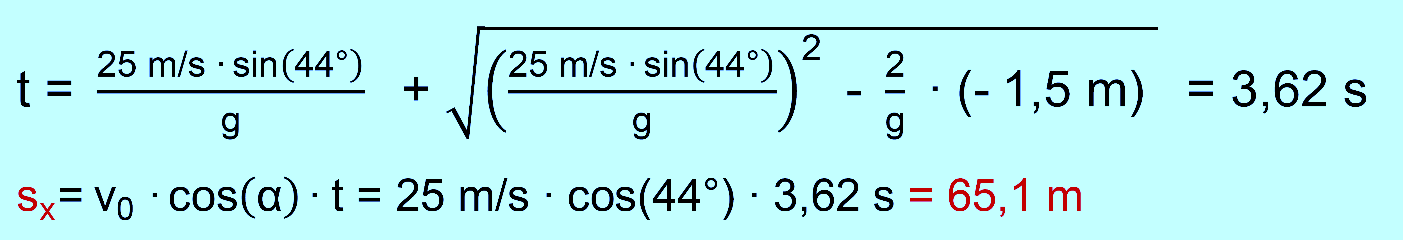|
- erste
Klausuraufgabe: Kugelstoßen - vierte Klausuraufgabe: Basketball - zweite Klausuraufgabe: Fußball -
fünfte Klausuraufgabe: Hammerwurf - dritte
Klausuraufgabe: Volleyball Sport und Physik 1. Klausuraufgabe − Kugelstoßen (mittel) Ein Kugelstoßer wirft seine 7,26 kg schwere Kugel aus einer Höhe von 1,85 m in einem Abwurfwinkel von 45° mit einer Anfangsge- schwindigkeit von v0 = 14 m/s ab. Es soll ein reibungsfreier Ablauf
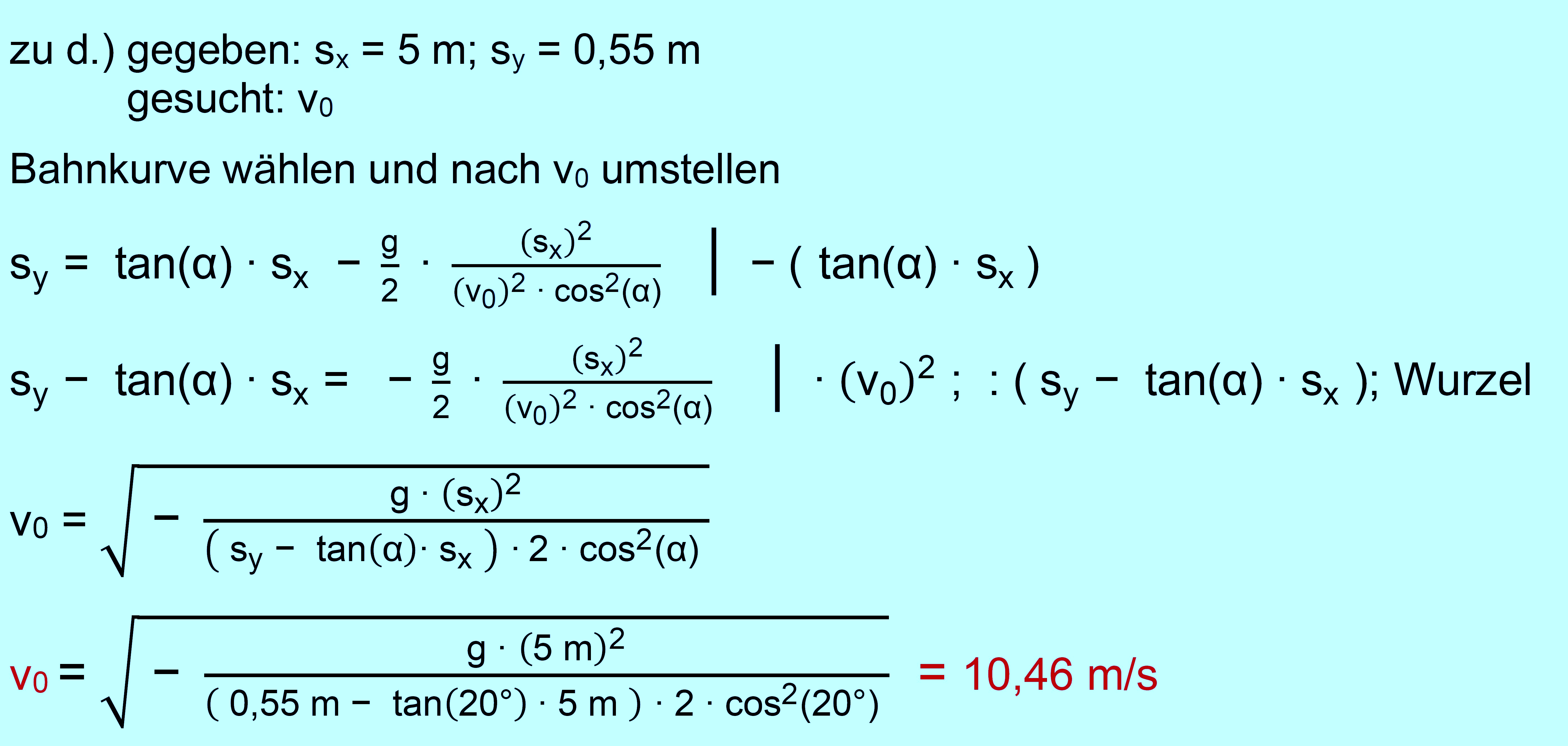
betrachtet werden. a.) Nach welcher Zeit hat die Kugel in der Horizontalen eine Strecke von 12 m zurückgelegt? In welcher Höhe über dem Erdboden befindet sich die Kugel zu diesem Zeitpunkt? (einfach) b.) Bestimme die größte Höhe und die Gesamtweite, die der Kugel- stoßer erreicht. (einfach,mittel) c.) Randy Barnes hielt bis 2022 den Weltrekord im Kugelstoßen mit 23,12 m. Er ist 1,94 m groß. Nehmen Sie an, dass er die Kugel in 2,10 m Höhe mit einer Anfangsgeschwindigkeit von 15 m/s abwirft. Welche Geschwindigkeit weist die Kugel dann beim Auftreffen auf dem Boden auf? Welchen Abwurfwinkel hat Randy gewählt, wenn die Kugel 2 s in der Luft ist?(mittel) zu a.) und b.) gegeben: sx = 12 m,
h0 = 1,85 m, α = 45°, v0 = 14 m/s, m = 7,26 kg gesucht: a.) t, sy b.) hmax , smax = w
zu b.)
zu c.) 1.Teil gegeben: v0 = 15 m/s , h0 = 2,10 m, t = 1,5 s,
vG (1,5
s) = 12,56 m/s gesucht: α, vB = Geschwindigkeit auf dem
Boden
zu c.) 2.Teil 1.) ohne Energieerhaltungssatz: - zunächst die Berechnung der Flugzeit bis zum Boden ( sy
= − 2,10 m)
2.) mit Energieerhaltungssatz:
Man erkennt sofort, dass dieser Teil mit dem
Energieerhaltungssatz deutlich schneller und einfacher zu lösen ist. Deshalb
macht es Sinn, sich mit diesem Kapitel
auf jeden Fall zu beschäftigen. 2. Klausuraufgabe − Fußball (mittel bis schwer) a.) Ein Spieler tritt beim Fußballspiel einen Freistoß direkt vom
Mittel- punkt in Form eines schiefen Wurfes auf das Tor. Der Ball kommt genau auf der Torlinie auf, wenn kein Torwart eingreift. Der Abstand zwischen Abschusspunkt und Torlinie beträgt 52 m. Die Abschuss- geschwindigkeit ist v0 = 108 km/h. Hinweis: Der Ball wird als Punkt angesehen.
Es liegt keine Reibung vor. 1.) Bestimmen
Sie den Abschusswinkel und die größte Flughöhe. Berechnen Sie die Flugdauer. [Zur
Kontrolle: α = 17,26°](mittel, einfach) 2.) Der
Torwart steht 16 m vom Tor entfernt gerade noch im Strafraum. Er befindet sich dabei genau auf der
Fluglinie des Balles, d.h. der Ball fliegt genau auf ihn zu. Zeigen Sie,
dass der Torwart den Ball in dieser Position nicht fangen kann, wenn die
größte Höhe, die der Torwart mit den Händen erreichen kann, 3,3 m sind.(mittel) b.) Zlatan
Ibrahimovic gelang in einem Freundschaftsspiel gegen England im Jahr 2012 ein legendärer
Fallrückzieher. Sieht man sich das Video an, so beträgt die
Gesamtflugzeit 2,6 s. Die größte Höhe erreicht der Ball nach 1,20 s. Die
Entfernung zwischen Abschusspunkt (am Boden gemessen) und dem
Auftreffpunkt beträgt 25 m. Bestimmen Sie aus diesen Daten die
Abschussgeschwindigkeit und den Abschusswinkel. (schwer) [ Zur Kontrolle: v0
= 15,20 m/s; α = 50,76 °] Bestimmen Sie mittels der
Lösungsdaten (Sie können auch die Kontrolldaten wählen) und den vorgegebenen Daten die Höhe
des Abschusspunktes über dem Boden(mittel,schwer) Zusatzaufgabe zu b): Wie weit hätte der Torwart herauslaufen dürfen, um den Ball noch zu fangen (Annahme: größte Fanghöhe 3,3 m)?(schwer) Video zu b.) zu a.) 1.) Da vom Boden aus geschossen
wird (h0 = 0 m), können die Formeln von sw , sh und tw
direkt übernommen werden gegeben: v0 = 108 km/h = 30 m/s, sw = 52 m
zu a.) 2.) gegeben: v0 = 108 km/h = 30 m/s, sw = 52 m , α =
17,26° , sx = 36 m = 52 m − 16 m gesucht: sy an der
Stelle sx = 36 m
3,44 m > 3,30 m , also nicht
zu fangen zu b.) − schwer: es fehlen beide wichtigen Größen (v0
und α), da nach ihnen gefragt wird →
man muss aus bekannten Formeln eine neue Formel entwickeln, die nur die gegebenen Größen enthält
Abschusspunkt über die y−Koordinate des Auftreffpunktes berechnen ; Abschusspunkt = Ursprung des Koordinatensystems
Zusatzaufgabe: Lösungsweg: an welcher Stelle sx liegt eine Höhe von 3,3 m vor → an welcher Stelle sx beträgt die y-Koordinate sy = + 0,75 m (3,3 − 2,55) Man hat zwei Möglichkeiten: 1.) Man wählt die Formel für die
Bahnkurve und stellt nach sx um, was ziemlich aufwendig ist. 2.) Man bestimmt zunächst die Zeit
bis zur Höhe von 0,75 m und setzt diese dann in die Bewegungsgleichung
für sx ein. Die zweite Möglichkeit hat den
Vorteil, dass schon alle Formeln vorliegen. Wir wählen die zweite Möglichkeit.
Im ersten Fall (Abwärtskurve) hätte der Torwart bis fast zur Torlinie zurücklaufen müssen, da der Ball ca.1 m hinter der Torlinie ins Tor fällt. Da der Torwart sich außerhalb des 16 m −
Raums befindet, als er den Ball unglücklich wegköpft, hat er keine Zeit mehr, um dorthin zu gelangen. Besser wäre gewesen,
dass er wie im zweiten Fall
(Aufwärtskurve) auf Ibrahimovic zuläuft, um den Ball direkt beim Abschuss wegzu- fangen. Er wäre dann zwar
vom Platz gestellt worden. Aber das wäre in der Nachspielzeit nicht mehr
so schlimm gewesen. 3. Klausuraufgabe − Volleyball (leicht-mittel) Beim einem Volleyballspiel wird ein unterer Aufschlag
senkrecht zum Netz in einer Höhe von 60 cm über dem Boden ausgeführt. Der Abwurfwinkel beträgt 25°. Die Abwurfgeschwindigkeit
sind 15 m/s. Der Abstand zur Netzebene liegt bei 10 m. Die
Netzoberkante befindet sich in einer Höhe von 2,35 m. a.) Wann erreicht der Ball die Netzebene?(einfach) b.) Zeige, dass der Ball über das Netz fliegt. Berechne
hierzu die Höhe des Balles in der Netzebene.(einfach) c.) Welches ist die größte Höhe, die der Ball erreicht.
Befindet sich der Ball dann schon auf der gegnerischen Seite?(mittel) d.) Nach welcher Zeit trifft der Ball auf dem Boden auf ( Annahme.
kein Gegner berührt den Ball )? Liegt der
Auftreffpunkt im gegnerischen Feld ? (mittel) ( Hinweis:
ein Volleyballfeld hat die Maße: 18 m lang, 9 m breit ). Runde auf Hundertstel
4. Klausuraufgabe − Basketball (einfach-schwer) Beim Basketball befindet sich die Korböffnung in einer Höhe von 3,05 m. Ein Basketballspieler versucht einen 3-Punktewurf aus einer Entfernung von 5 m. Er wirft den Ball in einer Höhe von 2,5 m mit der
Geschwindigkeit 10 m/s ab. Der Abwurfwinkel beträgt 20°. a.) Wann erreicht der Ball den Korbabstand von 5 m
?(einfach) b.) Trifft der Werfer direkt in den Korb? Begründe!(mittel) c.) Welche größte Höhe erreicht der Ball? Hat der Ball dann schon die
Hälfte des Korbabstandes zurückgelegt? Berechne!(einfach,mittel) d.) Mit welcher Geschwindigkeit muss der Werfer abwerfen, um den Korb bei sonst unveränderten Bedingungen direkt zu treffen?(schwer) Beachte: Der Durchmesser des Balls und des
Korbes wird nicht berücksichtigt! Beide werden als punktförmig angesehen.
Die
nächste Aufgabe ist sehr komplex, da Inhalte aus den Kapiteln: Kreisbewegung, Energieerhaltungssatz,
lotrechter Wurf und schiefer Wurf benötigt werden. 5. Klausuraufgabe − Hammerwerfen (schwer) Bei der Sportart "Hammmerwerfen"
wird eine eiserne Kugel mit der Masse m = 7,257 kg an einem Drahtseil durch Herumschleudern auf die Geschwindigkeit v gebracht. Die Kugel bewege sich auf einer exakten Kreisbahn. a.) Der Radius des Kreises sei die Summe aus der Drahtseillänge 1,22 m und der Armlänge 0,60 m. Die Kugel führt zwei Umdrehungen pro Sekunde durch. 1.) Welche Geschwindigkeit weist die Kugel dann auf? 2.) Mit welcher Kraft muss der Sportler die Kugel halten? (Hinweis: Sie dürfen FG
vernachlässigen) 3.) Wie groß ist die kinetische Energie der Kugel? b.) Welche Höhe würde die Kugel erreichen, wenn sie mit der kine- tischen Energie aus a.) 3.) senkrecht nach oben geworfen würde? (Höhe = Höhe über der Abwurfstelle) c.) Ein Hammerwerfer wirft die Kugel unter einem Winkel von 30° zur Horizontalen mit einer Geschwindigkeit von 25 m/s aus einer Höhe von 1,50 m ab. 1.) Bestimme die größte Höhe, die der Hammer jetzt erreicht. 2.) In welcher Entfernung vom Abwurfort wird die Kugel auf dem Erd- boden aufschlagen? d.) Im Kapitel „Optimaler
Wurfwinkel für maximale Weite“ gibt es eine Formel
für den besten Winkel, mit dem man abwerfen sollte. Daraus ergibt
sich, dass der optimale Winkel bei 44° liegt. Berechne hiermit noch
einmal die Wurfweite. Lösung: zu a.) einfach in die jeweiligen Formeln einsetzen
zu b.) über die Formel von sh berechnen oder
über den Energieer- haltungssatz
zu c.) Höhe über sh; Weite über sx
, wobei zunächst die Flugzeit be- stimmt wird.
zu d.)
- erste
Klausuraufgabe: Kugelstoßen - vierte Klausuraufgabe: Basketball - zweite Klausuraufgabe: Fußball -
fünfte Klausuraufgabe: Hammerwurf - dritte
Klausuraufgabe: Volleyball - zurück zum
Kapitel „Schiefer Wurf“ |