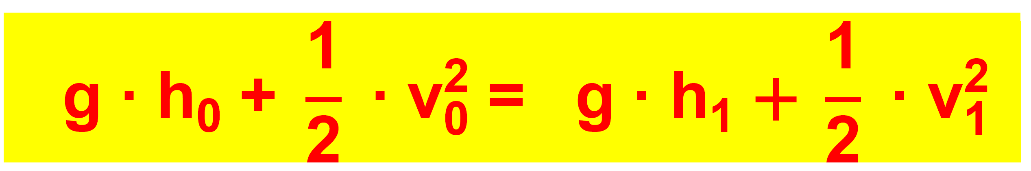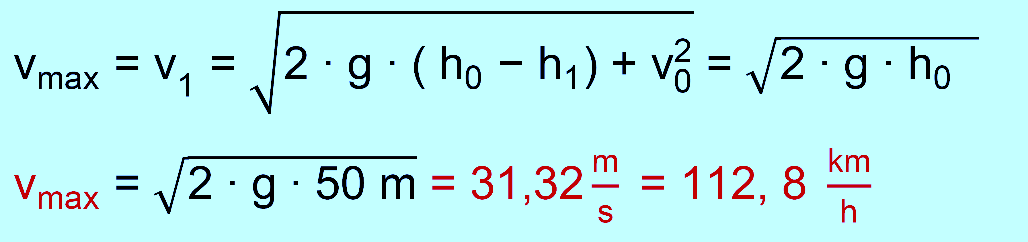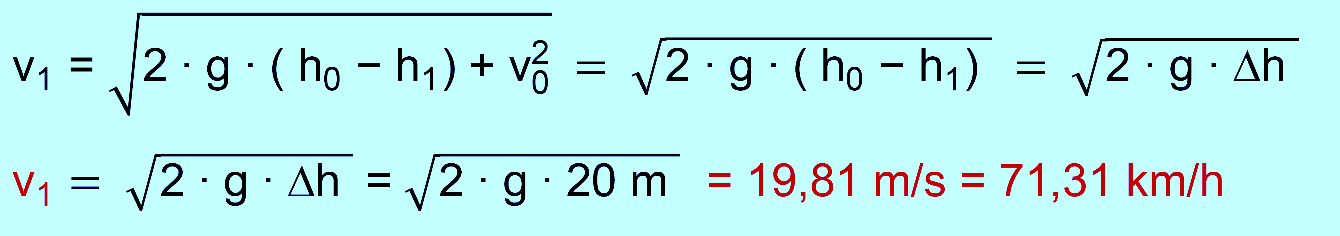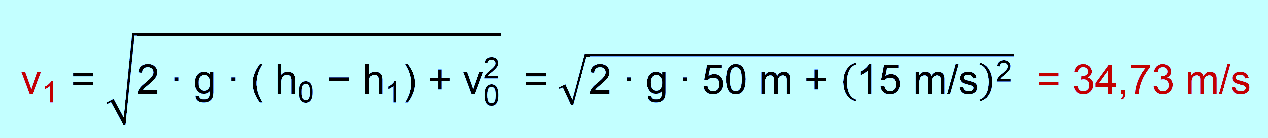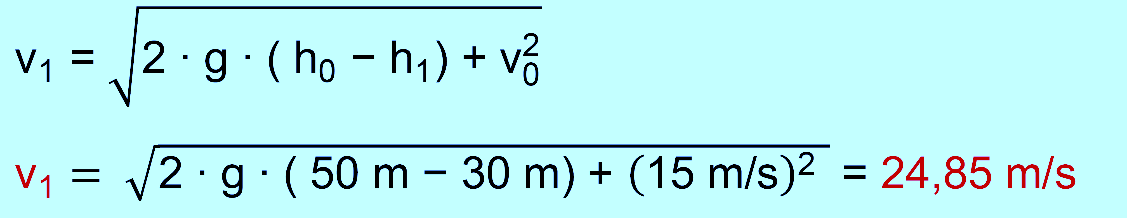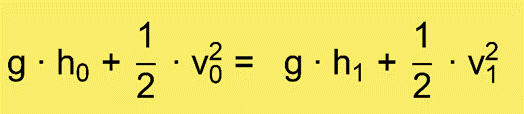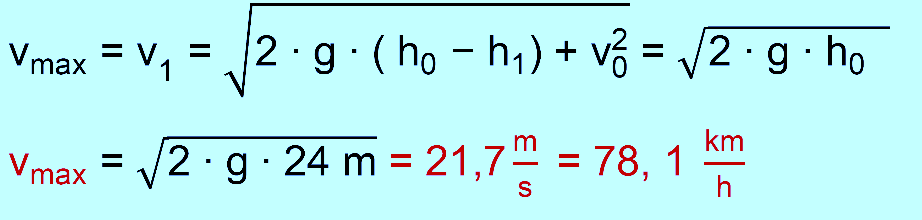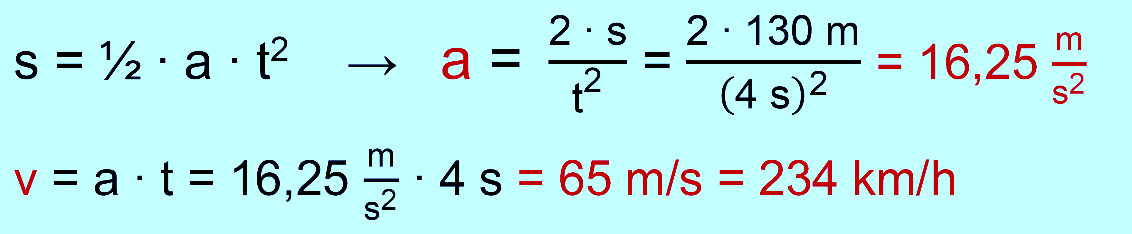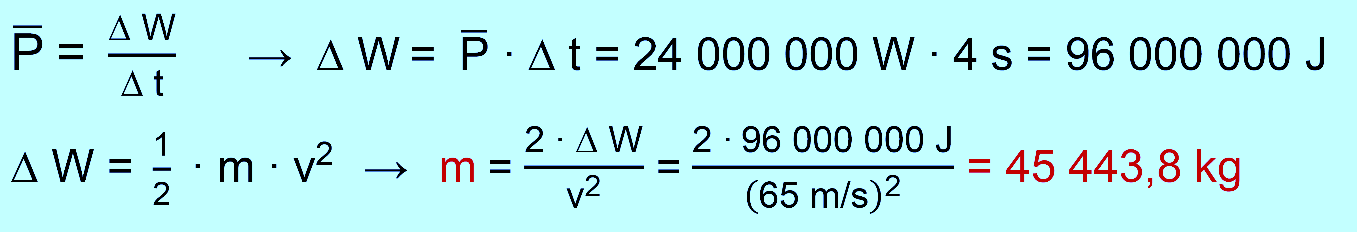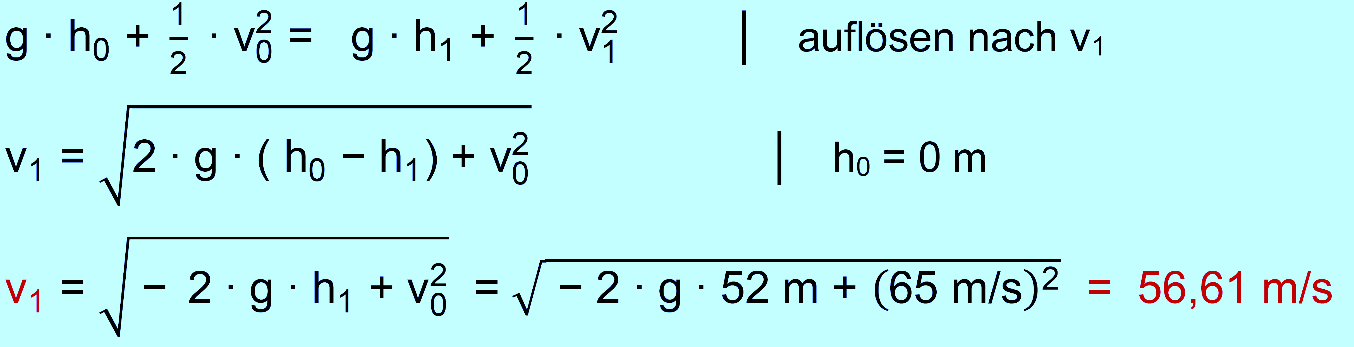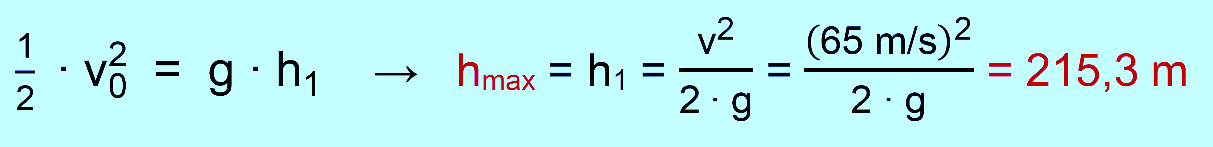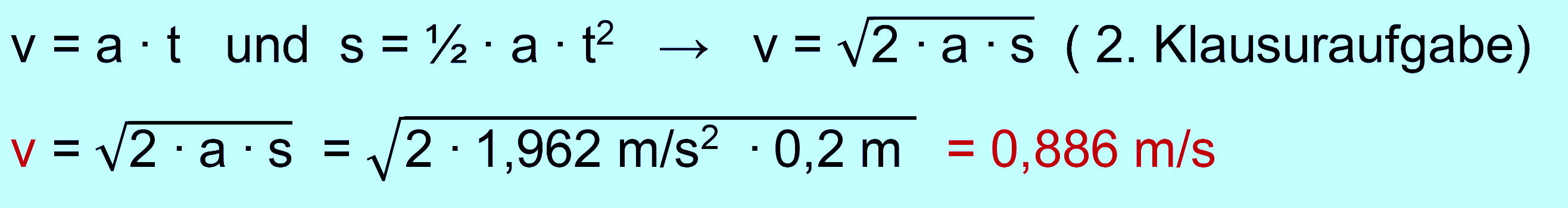|
Sprung zu: 1. Klausuraufgabe ( Holzachterbahn Colossos):
leicht, mittel 2. Klausuraufgabe
(Looping Star): mittel, schwer 3. Klausuraufgabe (Formula
Rossa): mittel, schwer 4. Klausuraufgabe (Massefahrstuhl): mittel, schwer 5.
Klausuraufgabe (Atwood): mittel, schwer Energieerhaltung
– Klausuraufgaben 1. Klausuraufgabe (leicht, mittel) Colossos ist die größte Holzachterbahn der Welt (im Jahr 2022). Bei dieser Achterbahn werden die Wagen auf eine Höhe von ca. 50 m hochgezogen (Lifthill). Die
Wagen fahren dann ohne An- fangsgeschwindigkeit die Achterbahn herunter. a.) Welche größte Geschwindigkeit kann die Achterbahn
erreichen? b.) Nach dem Absturz auf das Grundniveau steigen die Wagen
dann wieder
auf eine
Höhe von 30 m (Airtimehügel). Berechne die Ge- schwindigkeit auf dem Airtimehügel. c.) Berechne die Werte aus a.) und b.) noch einmal neu, wenn
die Wagen am höchsten Punkt noch mit einem Katapult auf 54 km/h (15 m/s) beschleunigt werden würden. Lösung: Wir
lösen die Aufgabe, wie so oft, mit der Grundgleichung und schauen,
welche Größen gegeben sind bzw. welche gesucht werden.
Die Grundgleichung lautet (s.Formeln).
zu a.) gegeben: h0 = 50 m, v0
= 0 m/s, h1 = 0 m (Erdboden) gesucht v1 zu b.) gegeben: h0 = 50 m, v0
= 0 m/s, h1 = 30 m (Airtime) gesucht v1
zu c.) 1.) gegeben: h0 = 50 m, v0
= 15 m/s, h1 = 0 m (Erdboden) gesucht v1
zu c.) 2.) gegeben: h0 = 50 m, v0
= 15 m/s, h1 = 30 m (Airtime) gesucht v1
Kombiaufgaben: Hinweis: ab hier werden die Aufgaben schwerer, da mehr als nur
der Energieerhaltungssatz abgefragt wird. Es kann auch um die
Bereiche: einfache Bewegungen,
komplexe Bewegungen, Leistung
gehen 2. Klausuraufgabe (mittel, schwer) Beim „Looping Star“, der ersten
transportablen Looping-Achterbahn, werden die Wagen zu Beginn 24 m
hochgezogen (Lifthill) und dann losgelassen. a.) Bestimmen
Sie die Geschwindigkeit der Wagen in km/h, wenn sie auf dem Boden ankommen. [ Zur Kontrolle: v1 = 21,70
m/s ] b.) Der
Looping hat eine Höhe von 14 m. Berechnen Sie die Ge- schwindigkeit der Wagen am höchsten Punkt des
Loopings. c.) Man möchte
jetzt die Bodengeschwindigkeit v1 als Startge- schwindigkeit durch ein Katapult erreichen. Dieses
beschleunigt die Wagen gleichmäßig am Boden auf die Geschwindigkeit v1,
wobei eine Beschleunigungsstrecke von 50 m zur Verfügung
steht. Bestimmen Sie die Zeitdauer der Beschleunigungsphase. Lösung: a.) und
b.) werden entsprechend der 1. Klausuraufgabe gelöst. Wir beginnen wieder mit der Grundgleichung usw.
zu a.) gegeben: h0 = 24 m, v0
= 0 m/s, h1 = 0 m (Erdboden) gesucht v1
zu b.) gegeben: h0 = 24
m, v0 = 0 m/s, h1 = 14 m (Looping) gesucht v1
zu c.)
es handelt sich um eine gleichmäßig
beschleunigte Bewegung. Wir
können also die entsprechenden Formeln anwenden. Es gibt allerdings
keine Formel, die v mit s verbindet. Diese muss also zu- nächst
hergeleitet werden. Dazu werden die bekannten Gleichungen nach t
aufgelöst und gleichgesetzt. Man erhält eine Formel zwischen v und a,
mit der man a bestimmen kann. Danach ist t einfach zu be- rechnen.
3. Klausuraufgabe (mittel, schwer) Die Katapult-Achterbahn „Formula Rossa“
in Abu Dhabi gilt als die schnellste Achterbahn der Welt. Bei
dieser Achterbahn werden die Wagen innerhalb von 4 s auf einer
Strecke von 130 m gleichmäßig beschleunigt. a.) Berechnen Sie die
Startgeschwindigkeit v1 der Wagen in km/h. [ Zur Kontrolle: v1 = 65
m/s] Die Achterbahn besitzt eine Leistung
von 24 000 000 W, um die Wagen zu beschleunigen. Bestimmen Sie
die Masse der Wagen. b.) Die größte Höhe, die die
Achterbahn aufweist, sind 52 m. Berechnen Sie die Geschwindigkeit, die
die Wagen in dieser Höhe haben. c.) Bei vielen Achterbahnen werden die
Wagen zunächst in die Höhe gezogen und dann heruntergelassen.
Bestimmen Sie die Höhe, auf die bei einer solchen Bahn die Wagen gezogen
werden müssten, um am Boden dieselbe Geschwindigkeit wie
die „Formula Rossa“ zu bekommen. Lösung: zu a.)
Formeln zur gleichmäßig
beschleunigten Bewegung wählen. Zunächst
a bestimmen und danach v mittels dieser Formeln.
Zum
zweiten Teil von a.): Es handelt sich um eine mittlere Leistung. Die
Formel wird zunächst nach der Arbeit aufgelöst. Mit dieser Be- schleunigungsarbeit wird die Masse bestimmt.
zu b.) Ansatz
über die Grundgleichung: gegeben:
h0 = 0 m, v0 = 65 m/s, h1 = 52 m gesucht: v1
zu c.) Ansatz
über die Grundgleichung: gegeben:
h0 = 0 m, v0 = 65 m/s, v1 = 0 m/s gesucht:
h1 = hmax
4. Klausuraufgabe (mittel; gleichmäßig beschleunigt,
schiefe Ebene,
Energieerhaltungssatz)
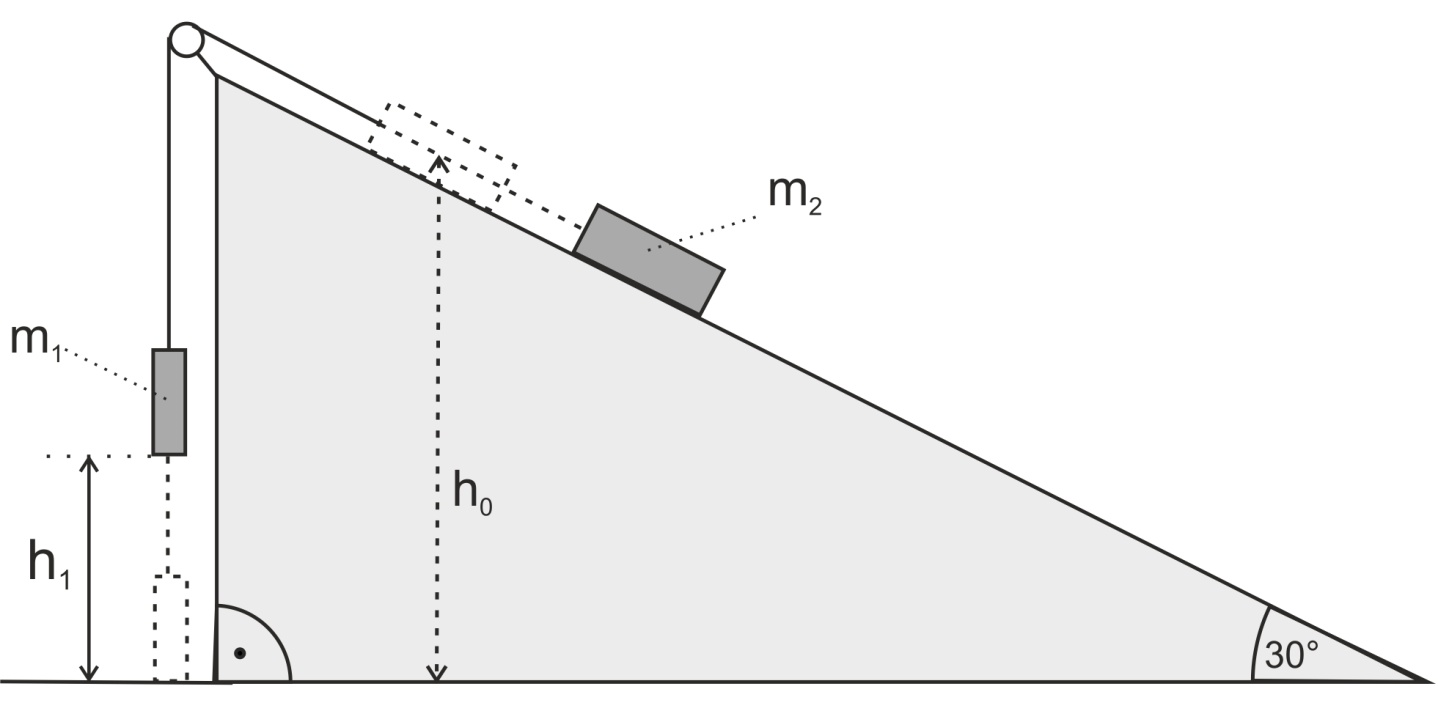
Der abgebildete Aufbau wird als Massefahrstuhl
bezeichnet. Eine große Masse m2 zieht eine kleine Masse
m1 nach oben. Beim Start befindet sich m1 auf dem
Erdboden. Das System be- wegt sich
nicht. Die kleine Masse m1 beträgt 2 kg, der große Körper hat eine Masse von m2 = 8 kg. Die
Schnur ist straff gespannt. m2 befindet sich beim Start in einer Höhe h0
von 10 m. Es liegt keine Reibung vor. Bestimmen Sie die Gesamtenergie des Systems am Start. Begründen Sie, welche Bewegungsform nach dem Start
vorliegt. Berechnen Sie die Beschleunigung des Systems. Bestimmen
Sie die Zeit t1 (seit dem Start), die der
Fahrstuhl braucht bis m1 eine Höhe h1 von 5 m erreicht hat [ Zur Kontrolle: t1 = 2,258
s ] . Welche kinetische Energie besitzt dann der Gesamtaufbau? Wie
groß ist zum Zeitpunkt t1 die gesamte
Lageenergie? Welche Lage- energie
weisen die einzelnen Massen auf? In welcher Höhe be findet daher zum Zeitpunkt t1 die Masse m2 ? [Zur Kontrolle: h=7,5 m ] Lösung:
Die beschleunigende Kraft ist konstant. Sie entspricht der Diffe- renz zwischen der Hangabtriebskraft von m2 und der Gewichts- kraft von m1. Deshalb liegt eine gleichmäßig beschleunigte Bewegung vor.
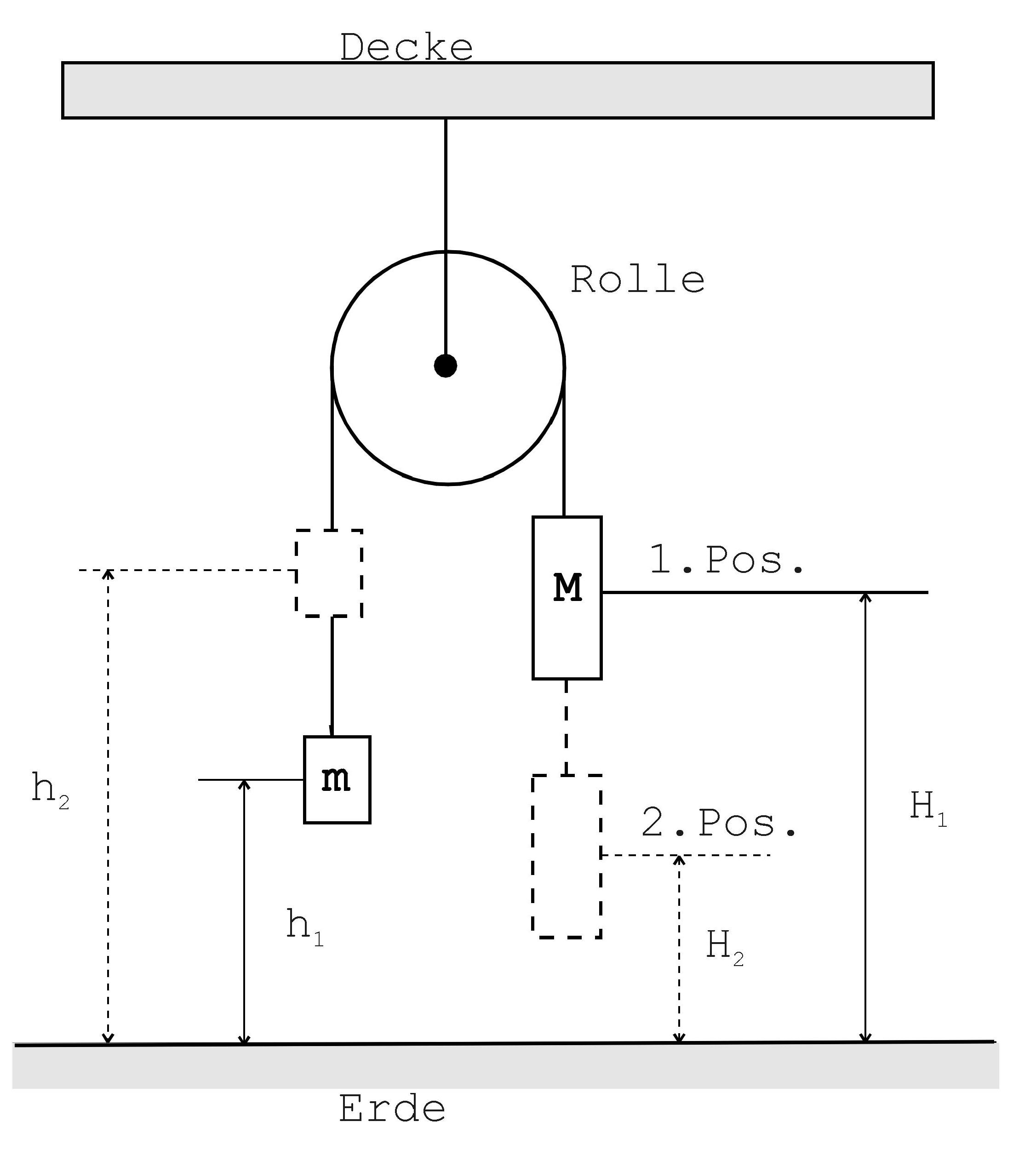
5. Klausuraufgabe (mittel-schwer; gleichmäßig beschleunigt, Energie- erhaltungssatz) In der Abbildung
ist eine Atwoodsche Fallmaschine abgebildet. Bei diesem Gerät
wird über eine große Masse M eine kleine Masse m gehoben. Die
Maschine soll sich zu Anfang in Ruhe auf der 1. Position
befinden. Die Masse M wird losgelassen. Man betrachtet nach einiger
Zeit das bewegte System an der 2.Position (gestrichelt). Es sollen
folgende Werte gelten: m = 2 kg, M = 3 kg, H1 = 50 cm, H2 =
30 cm. a.) Bestimme
zunächst formelhaft und dann konkret die Beschleuni- gung des Systems. b.) Berechne die
Geschwindigkeit des Systems an der 2.Position. c.) Geben Sie in
Formelschreibweise an, wie sich die Gesamtenergie an den einzelnen Positionen zusammensetzt. Bestimmen
Sie hiermit die Höhe H2,
bei der das System genau die Geschwindigkeit 0,5 m/s aufweist. Hinweis: Sie
dürfen Werte einsetzen, wenn alle Terme mit H2 auf der linken Seite stehen.
Lösung: a.)
Wenn man die Formel
für „a“ nach „g“ umstellt, hat man eine „bequeme“
Möglichkeit die Fallbeschleunigung „g“ zu bestimmen. Links: -
ATWOODsche Fallmaschine | LEIFIphysik
- Atwoodsche Fallmaschine – Wikipedia b.)
c.)
Sprung zu: 1. Klausuraufgabe (
Holzachterbahn Colossos): leicht, mittel 2. Klausuraufgabe (Looping Star): mittel, schwer 3. Klausuraufgabe (Formula Rossa): mittel,
schwer 4. Klausuraufgabe
(Massefahrstuhl): mittel, schwer 5.
Klausuraufgabe (Atwood): mittel, schwer zurück zum Kapitel „Energieerhaltungssatz“ zurück zur Übersicht „Arbeit
und Energie“ |