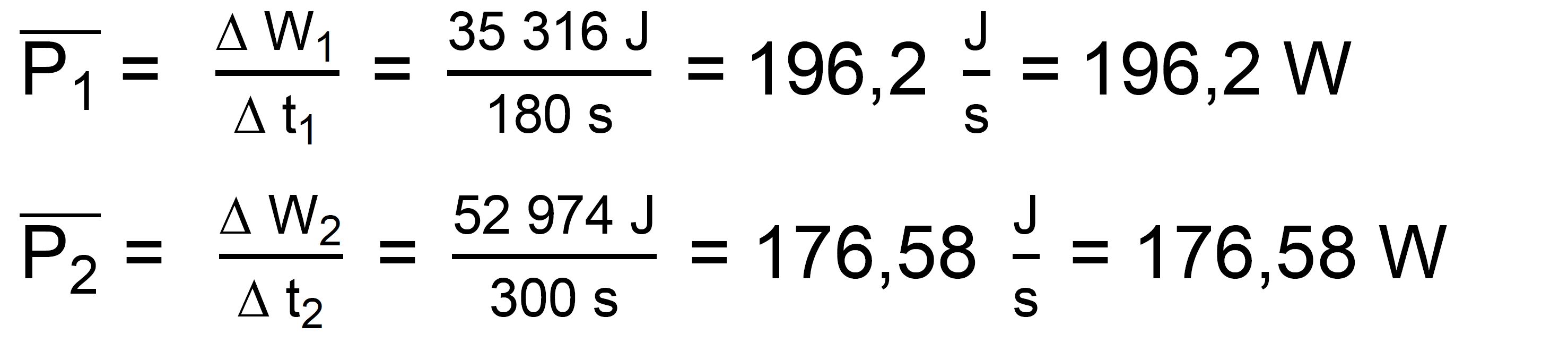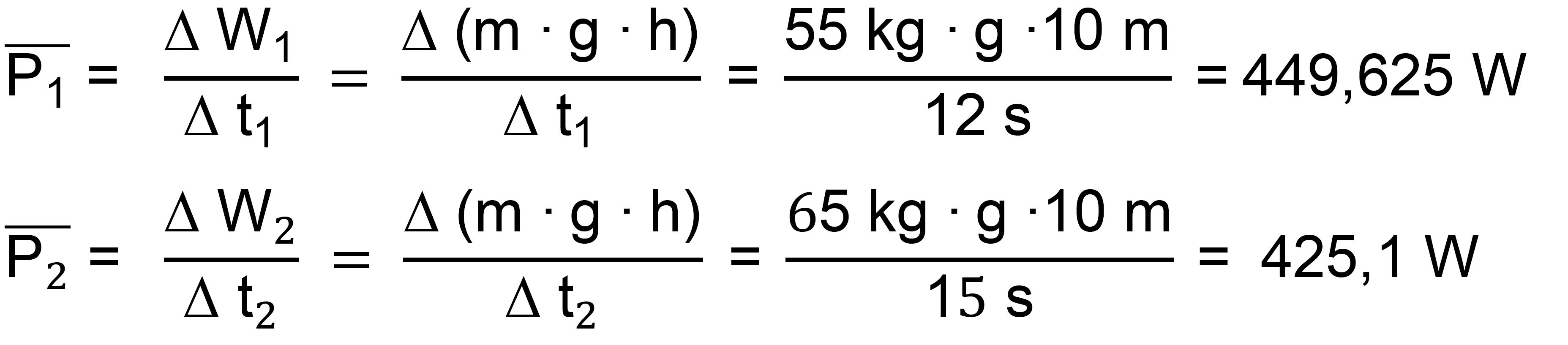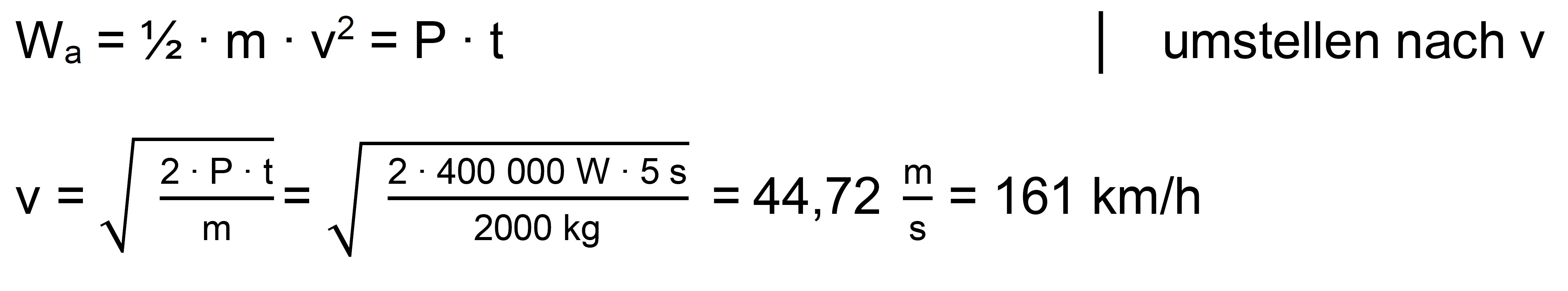|
nach unten
zur Momentanleistung
beispielaufgabe 1 treppenhaus
schüler
beispielaufgabe 2 marcel
kittel
beispielaufgabe 3 pkw
fahrt
Leistung
Durchschnittsleistung
Der Begriff „Leistung“ kommt häufig im
alltäglichen Sprachgebrauch vor:
„Man leistet viel oder wenig“, „Die
Leistung ist ungewöhnlich“ usw.
Ein kleines Beispiel zum Einstieg in
das Thema:
Der erste Maurer schleppt zwei
Zementsäcke in 3 Minuten in den dritten Stock.
Der zweite Maurer schafft drei
Zementsäcke in 5 Minuten in den dritten Stock.
Wer hat mehr geleistet?
Zunächst muss man wohl auf die gleiche
Zeit zurückrechnen, z.B. auf eine Minute:
Maurer 1: 2/3 Säcke in einer Minute
Maurer 2: 0,6 Säcke in einer Minute
Also schafft der erste Maurer mehr
Säcke in einer Minute in den dritten Stock.
Er leistet mehr.
Bei der Leistung spielt also die Zeit,
in der etwas geschafft wird, eine entscheidende Rolle.
Wir erhalten also folgende Definition
Für unser kleines Beispiel gilt: m
(Zement) = 50 kg, h = 12 m (3. Stock)
beide Maurer haben jeweils eine Masse
von 100 kg
∆ W1 = m ∙ g ∙
h = 2 ∙ 150 kg ∙ g ∙ 12 m = 35 316 J ; t1 = 180 s
∆ W2
= m ∙ g ∙ h = 3 ∙ 150 kg ∙ g ∙ 12 m = 52 974 J ; t2
= 300 s
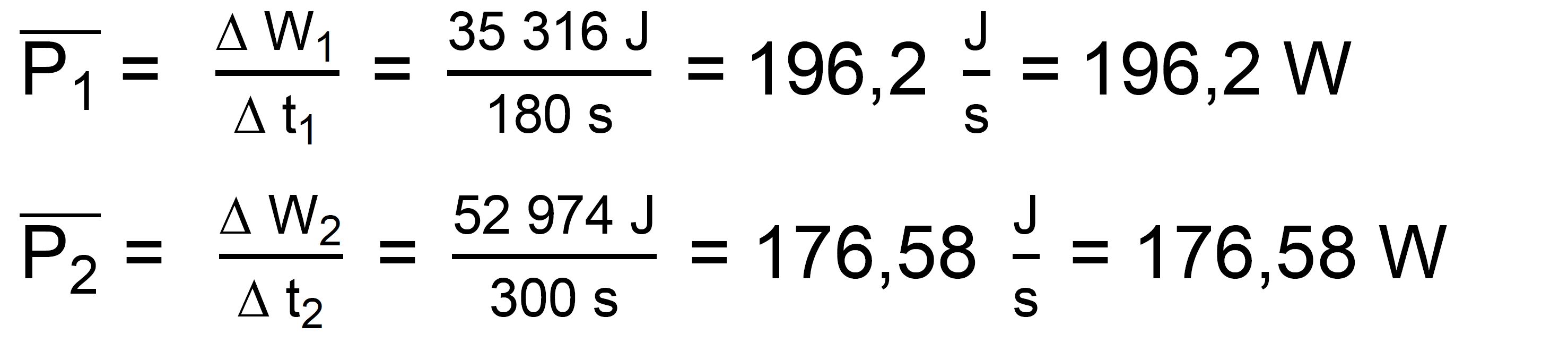
Der
erste Maurer leistet also mehr als der zweite Maurer.
Beispielaufgaben
|
1.
Aufgabe
Zwei Schüler rennen im Treppenhaus
der Schule um die Wette. Sie
starten im Erdgeschoss
und laufen in den zweiten Stock. Der zweite
Stock liegt 10 m höher
als das Erdgeschoss. Der erste Schüler hat eine
Masse von 55 kg, der
zweite eine Masse von 65 kg. Der erste Schüler
schafft die Strecke in
12 s, der zweite in 15 s.
Wie groß ist die
Leistung der einzelnen Schüler?
Lösung:
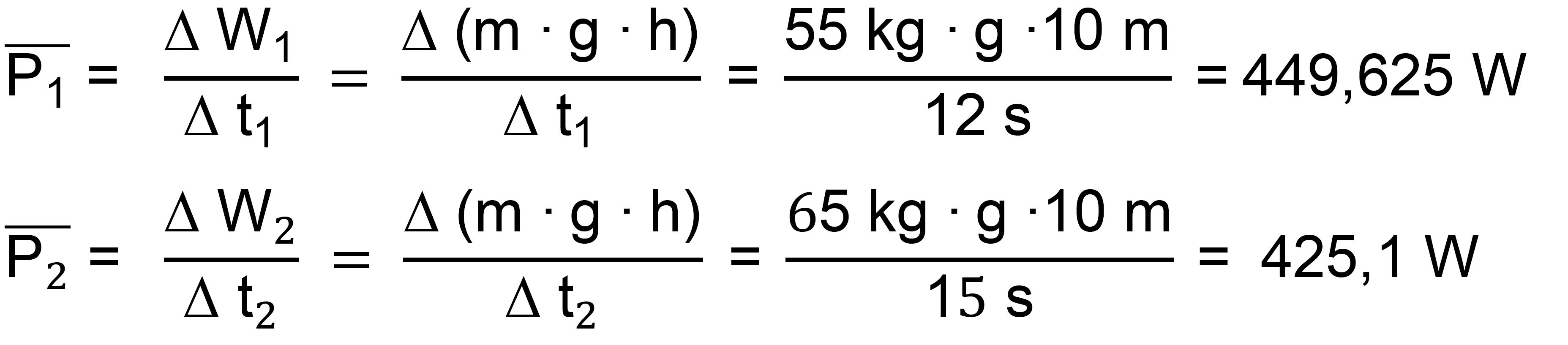
2.
Aufgabe
Marcel Kittel ist ein
ehemaliger deutscher Radrennfahrer der Tour
de France. Er konnte als
Sprinter kurzzeitig eine Leistung von 1900 W
mit dem Rad erreichen.
Marcel Kittel möge mit dem Rad von 0 km/h
auf 54 km/h mit
maximaler Leistung (gleichmäßig)
beschleunigen. Die Gesamtmasse ( Körper + Rad )
soll 95 kg betragen.
a.) Wie lange braucht er
für den Beschleunigungsvorgang?
b.) Wie groß ist die
Beschleunigung und welche Strecke legt er während
der Beschleunigung zurück?
Lösung:
zu a.) gegeben: P = 1900 W, m = 95 kg, vStart
= 0 m/s,
vEnde
= 54 km/h = 15 m/s
gesucht: t
Die verrichtete Arbeit ist Beschleunigungsarbeit.
Es gilt dann
Wa = ½ ∙ m ∙ v2 = ½
∙ 95 kg ∙ (15 m/s)2 = 10 687,5 J
mit der Formel zur Leistung ergibt sich
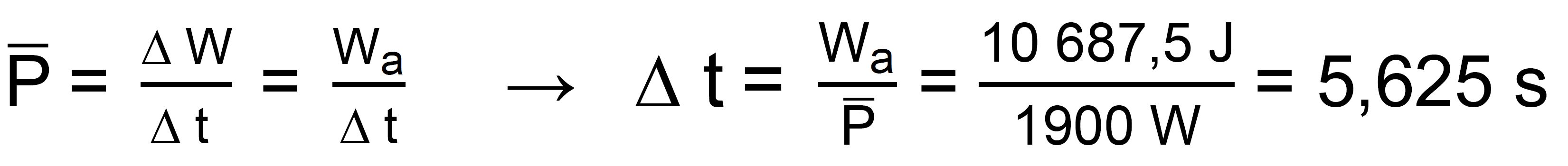
zu b.) Formeln zur gleichmäßig
beschleunigten Bewegung benutzen
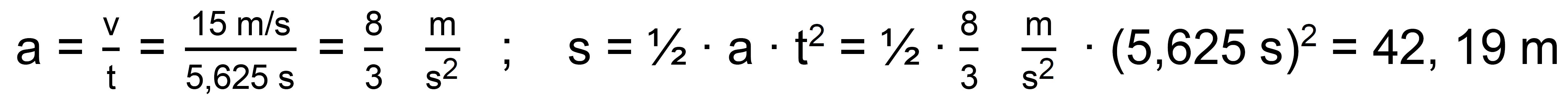
|
Momentanleistung
Aus
der Mathematik (s Link-Liste) wissen wir, dass der Durchschnittswert
(Mittelwert)
der Sekantensteigung (mittlere Änderungsrate)
entspricht.
Der
Momentanwert ergibt sich aus der Tangentensteigung oder Ableitung
(momentane
Änderungsrate).
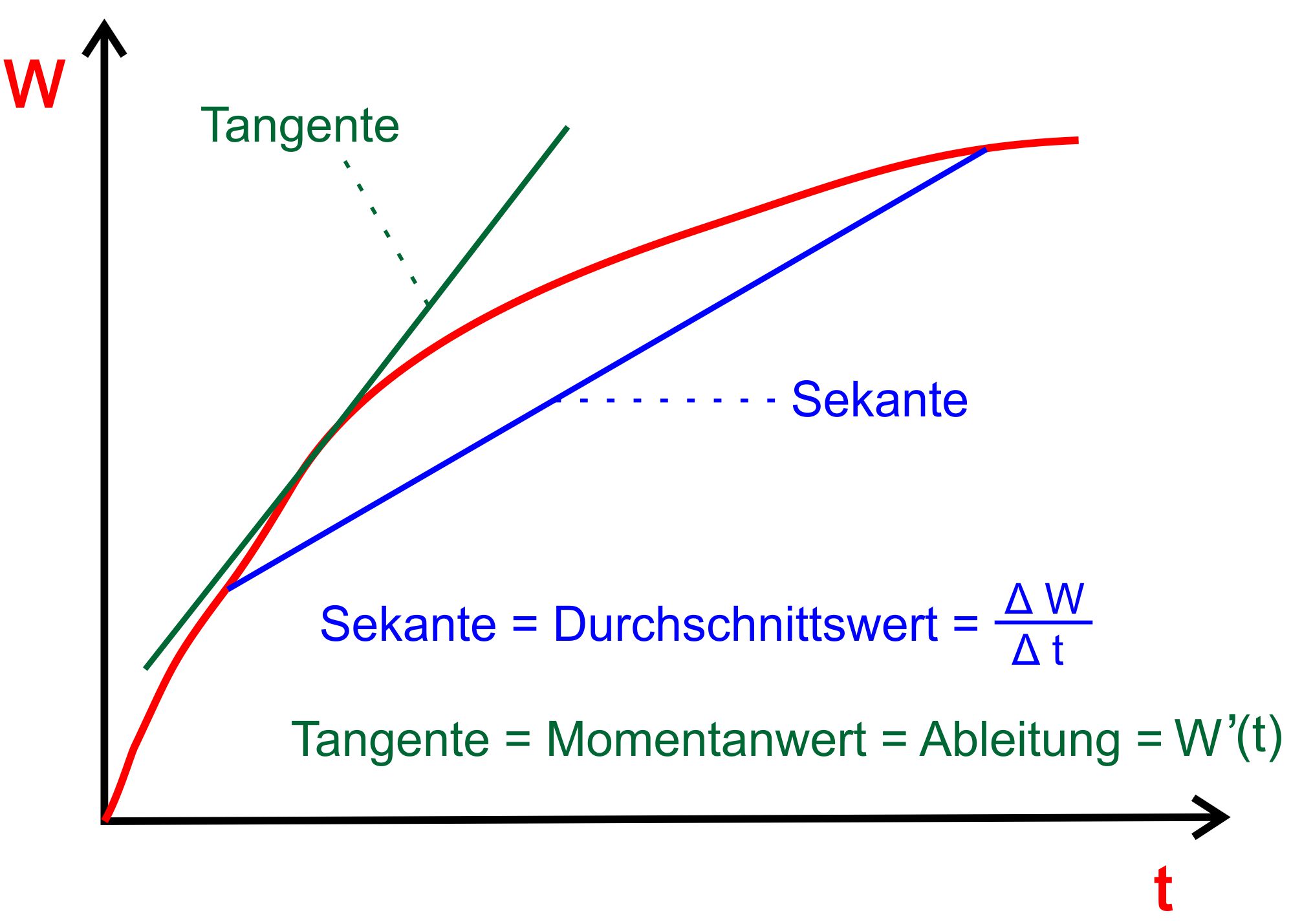
Bei
der Leistung geht es um ein Diagramm, in dem die verrichtete Arbeit W
gegen
die Zeit t aufgetragen wird.
In
der folgenden Abbildung sieht man noch einmal die Verhältnisse.
Hinweis zu den Gleichungen: „Sekante“ bedeutet Sekantensteigung, „Tangente“
bedeutet Tangentensteigung
Für
die Momentanleistung heißt dies jetzt:
|
Momentanleistung = P ( t ) = W ‘ (t)
|
Um
die Momentanleistung zu bestimmen, muss man also W(t) kennen.
Dann
kann man die Ableitung aufstellen und damit die Leistung berechnen.
Hinweis: Solch ein Fall kommt in der Schule
praktisch nicht vor
Die
Formel kann aber dazu dienen für den Fall einer konstanten Kraft F
eine
einfache
Formel herzuleiten. Es gilt nämlich dann:
Hinweis:
Wir verwenden statt der „Strich-Schreibweise“ die in der Physik übliche
„Differenzenschreibweise“ bzw.
„Differentialschreibweise“
oder auch „Leibniz-Notation“ für die Ableitung

Falls also F =
konstant während der
Arbeitsverrichtung, gilt folgende einfache
Formel:
|
Falls F = konstant ergibt
sich
P ( t ) = F ∙
v(t) ,
F = konstant
|
Beispielaufgabe
|
3. Aufgabe:
a.) Ein PKW hat eine maximale Leistung von 110 kW
und fährt dauerhaft
mit einer Höchstgeschwindigkeit von 216 km/h.
Welche Widerstandskraft
muss der PKW überwinden?
b.) Es gibt Elektro-PKWs die Leistungen von 400 kW
aufbringen können.
Die Masse eines solchen PKWs soll 2 t betragen. Die
Leistung soll nur
zur Beschleunigung des PKWs benutzt werden. Der PKW
beschleunigt
gleichmäßig aus dem Stand 5 s lang mit
maximaler Leistung.
Welche Geschwindigkeit hat er nach 5 s erreicht?
Wie groß ist die Beschleunigung?
Bestimme die Beschleunigungskraft und die
Beschleunigungsstrecke.
Lösung:
zu a.) gegeben P = 110 kW = 110 000 W, v = 216 km/h
= 60 m/s
gesucht: Widerstandskraft F
Der PKW fährt mit konstanter
Geschwindigkeit. Man könnte denken,
dass es nach dem Trägheitssatz
keine Kraft geben müsste. Wir haben
aber in diesem Fall keinen reibungsfreien
Fall vorliegen. Es gibt Reibung
durch den Luftwiderstand und den
Rollwiderstand. Diese abbremsenden Kräfte müssen durch die Motorkraft
ausgeglichen werden. Man hat ein
Kräftegleichgewicht vorliegen.
Die resultierende Kraft ist tatsächlich
Null.
Uns interessiert aber die
Motorkraft, die ja der Widerstandskraft ent-
spricht.

zu b.) gegeben: P = 400 kW = 400 000 W, m = 2 t = 2000
kg,
t = 5 s
gleichmäßige
Beschleunigung
Es wird nur
Beschleunigungsarbeit verrichtet. Wir gehen von einem
reibungsfreien Fall aus. Die
Beschleunigungsarbeit lässt sich auf zwei
Arten ausdrücken.
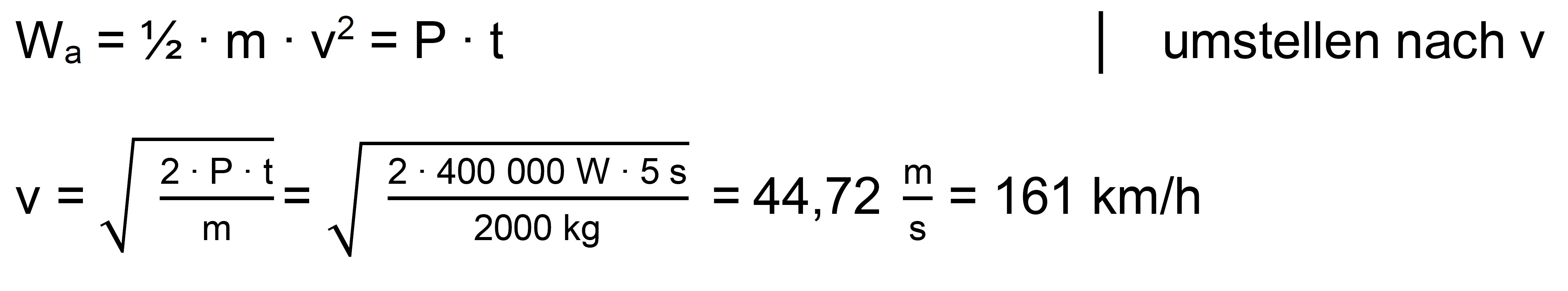
Es werden die Formeln für die
gleichmäßig beschleunigte Bewegung
benutzt.

|
|
Liste von Links:
-
https://abimathe.de/lernvideos/die-bedeutung-der-ersten-ableitung/
Bedeutung der Ableitung, Änderungsrate, Durchschnittwert,
Momentanwert
- https://www.wienenergie.at/blog/der-mensch-in-watt/
Leistungsangaben für den menschlichen Körper (hier ok)
Hinweis: viele Angaben über die Leistung
des Menschen auf Internetseiten erscheinen
mir falsch zu sein. Es wird auch immer noch die Einheit kcal oder
sogar cal für die Arbeit
benutzt. Auch Trainingsgeräte benutzen
häufig diese Angaben. Man sollte bei diesen Angaben vorsichtig sein und
genau nachrechnen. Wenn man die Werte in Leistungsangaben in Watt
umrechnet, kommt man zu völlig illusorischen Angaben
|
nach oben
zur Momentanleistung
beispielaufgabe 1 treppenhaus
schüler
beispielaufgabe 2 marcel
kittel
beispielaufgabe 3 pkw
fahrt
|