Mechanische Schwingungen

Definition: Schwingung

Schwingungen sind zeitlich periodische (sich wiederholende) Zustands-änderungen um einen festen Punkt, der Ruhelage (Nullpunkt, Gleich-

gewichtslage) genannt wird.

Einige typische Beispiele, die wir auch genauer untersuchen werden, ist das Federpendel und das Fadenpendel.

Beim Federpendel wird an eine vertikale Schraubenfeder eine Masse gehängt und durch Ausdehnung der Feder von außen zum Schwingen gebracht. Beim Fadenpendel befindet sich an einem vertikal aufgehängten Faden eine Masse, die durch Anstoßen in Schwingungen versetzt wird. Das Fadenpendel hat große Ähnlichkeit mit einer Schaukel.

Beispiel: Federpendel; Beispiel: Fadenpendel

https://commons.wikimedia.org/wiki/File:Simple_harmonic_oscillator.gif         https://commons.wikimedia.org/wiki/File:Pendelschwingung.gif   lizenzfrei

lizenzfrei

Das Feder- und das Fadenpendel gehören zu den mechanischen Schwingungen, da bei ihnen eine Masse schwingt.

Wir müssen zunächst einige Fachbegriffe klären, die für das Verständnis wichtig sind.

Ruhelage:

Die Ruhelage ist der „Symmetriepunkt“ der Schwingung, d.h. um ihn herum findet die periodische Bewegung statt.

Falls die Schwingung zum Stillstand käme, würde die Masse hier zur Ruhe kommen.

Umkehrpunkte:

Die Umkehrpunkte sind die Punkte, in denen die Bewegungsrichtung der Masse sich ändert, also die äußeren Punkte der Schwingung.

Schwingungsdauer T

Die Schwingungsdauer T ist die Zeit, die man für eine vollständige Schwingung braucht. Eine vollständige Schwingung liegt vor, wenn sich der Bewegungsablauf wiederholt, d.h. wenn ein Bahnpunkt wieder in der gleichen Richtung durchlaufen wird. Am einfachsten kann man die Schwingungsdauer messen, indem man die Zeitdauer bis zum Erreichen desselben Umkehrpunktes misst.

Frequenz f

Die Frequenz gibt die Anzahl der Schwingungen für eine Sekunde an.

Es gilt folgender Zusammenhang zwischen Schwingungsdauer und Frequenz

(siehe Kreisbewegung)

Elongation s

Unter der Elongation s versteht man die zu dem Zeitpunkt t vorliegende Entfernung der Masse von der Ruhelage. Es geht dabei aber um die zurückgelegte Strecke. Je nach der Lage der Masse hat die Elongation unterschiedliche Vorzeichen, ist somit eine vektorielle Größe.

Amplitude

Die Amplitude ist die größte Elongation, d.h. also die Entfernung (als Wegstrecke) zwischen Ruhelage und Umkehrpunkt.

gedämpfte und ungedämpfte Schwingung

Bei der ungedämpften Schwingung ist die Amplitude konstant, bei der gedämpften Schwingung nimmt die Amplitude ab.

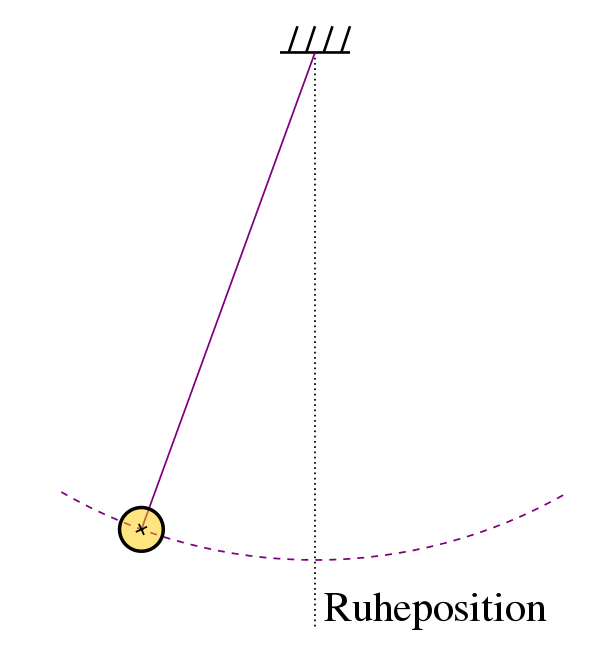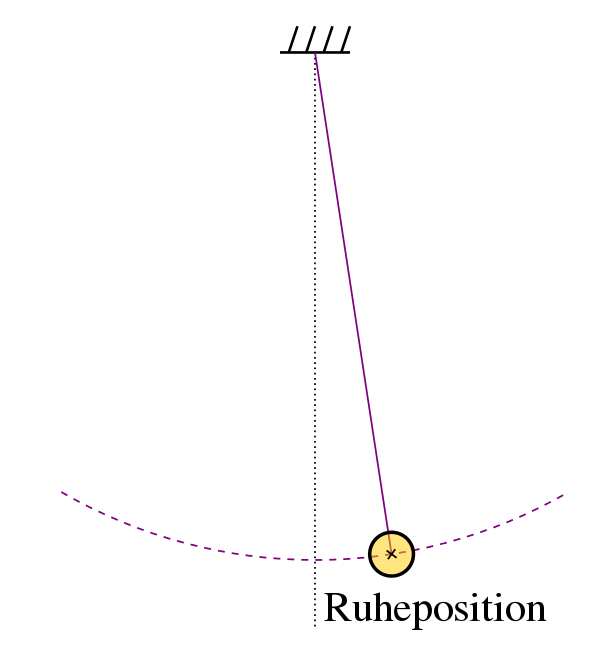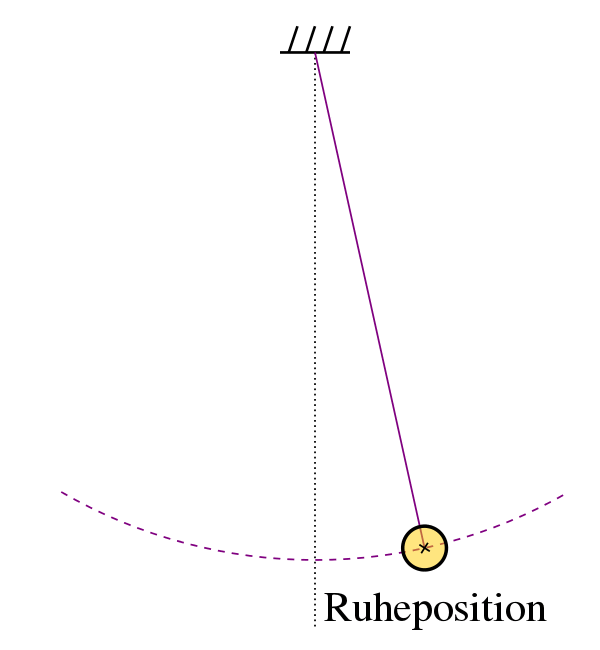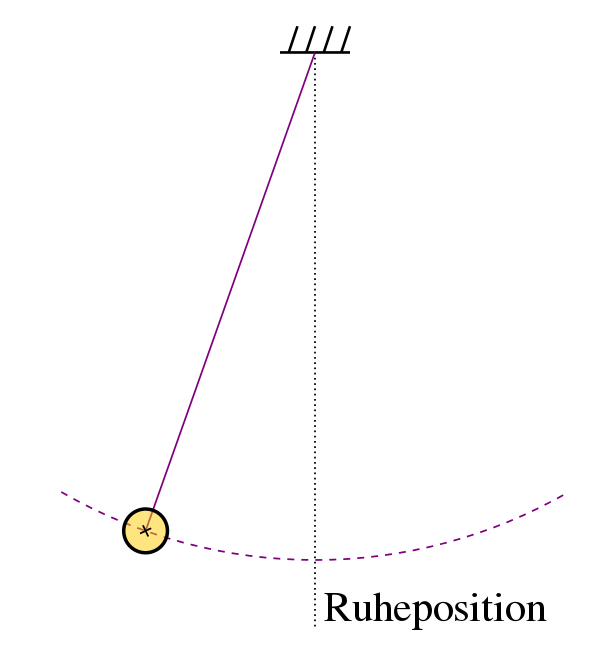
Hier die Erklärung anhand der Abbildung:

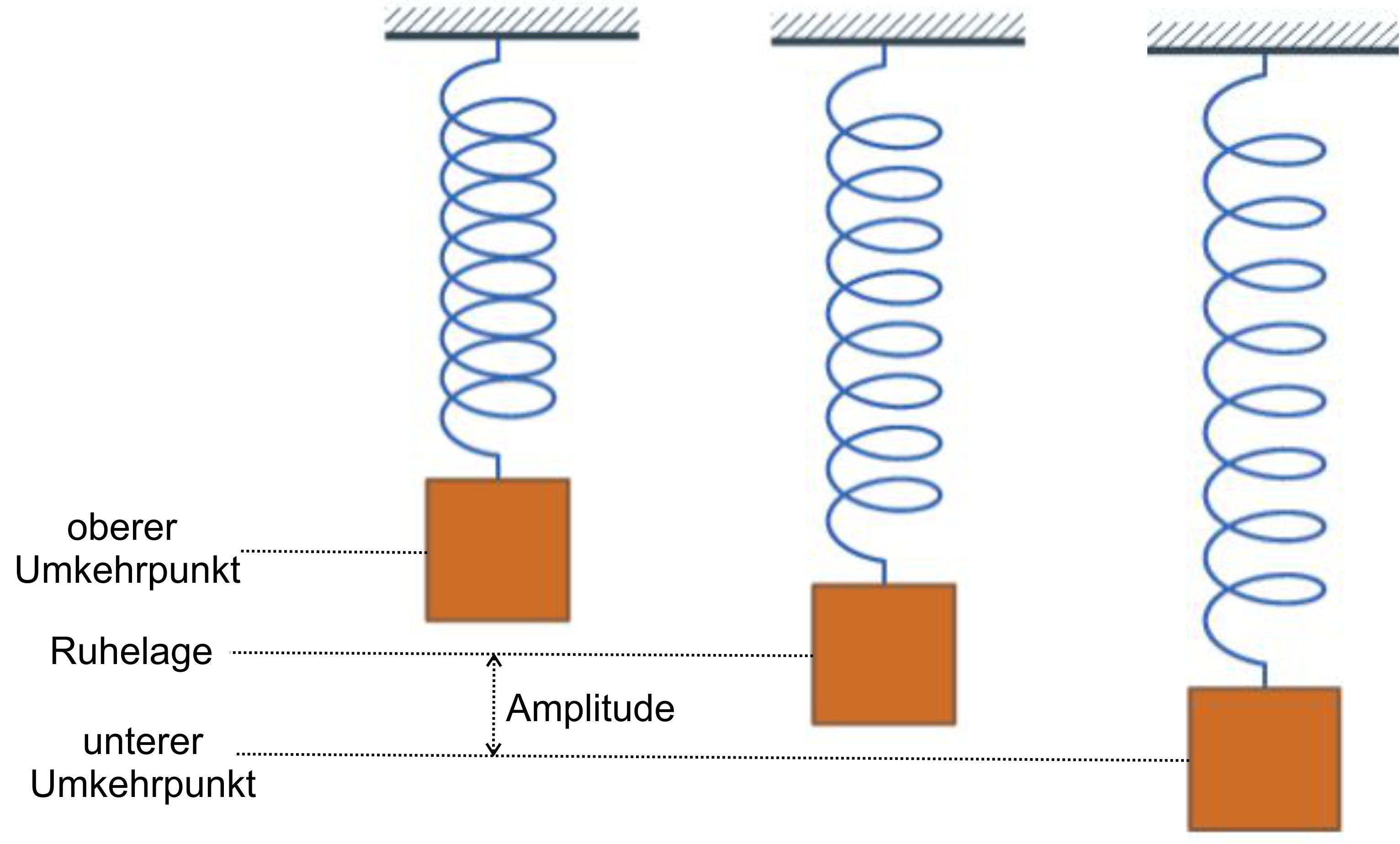
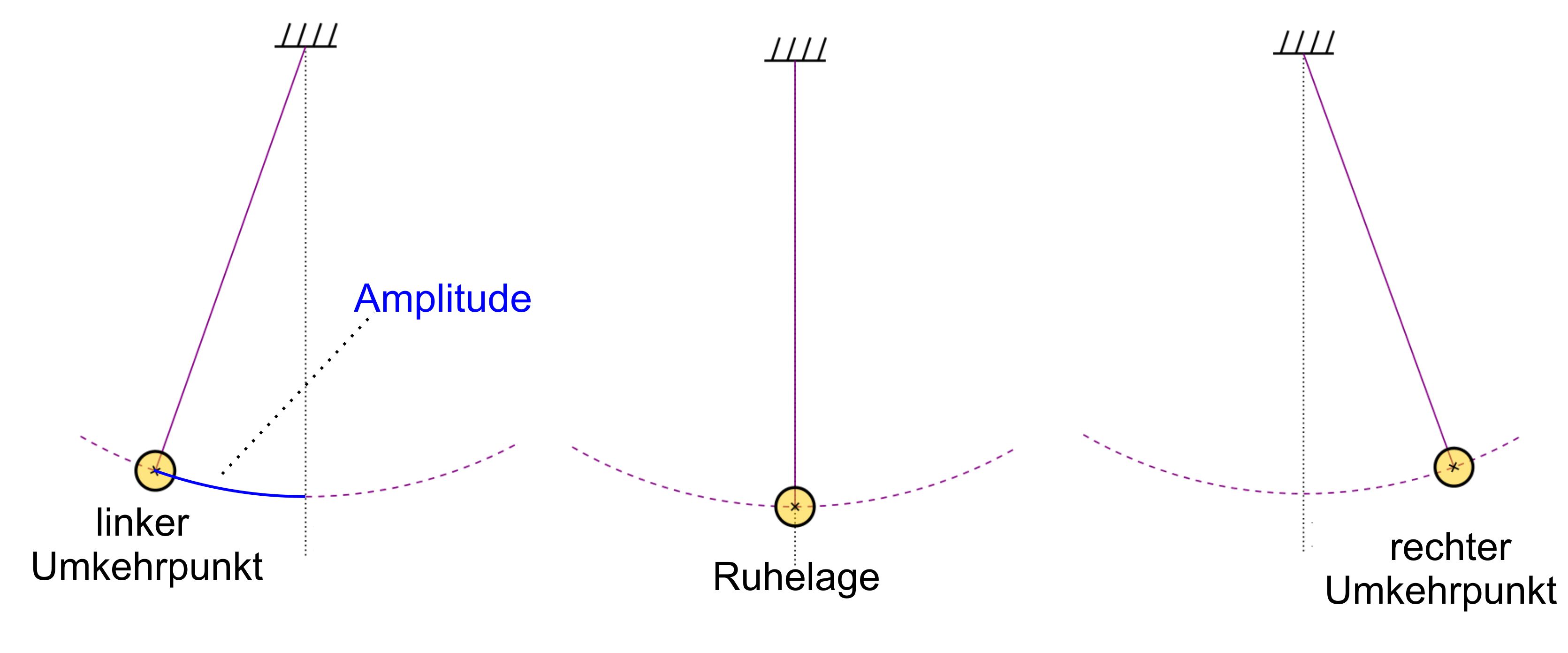
Man beachte beim Fadenpendel, dass die Amplitude die größte Kreisbogenlänge ist, entsprechend ist auch die Elongation die Kreisbogenlänge zu einem bestimmten Zeitpunkt.

Rückstellkraft

Da sich bei einem Schwingungsvorgang laufend die Geschwindigkeit ändert, muss es sich um eine beschleunigte Bewegungen handeln, d.h. es muss eine Kraft (2.Axiom von Newton = Grundgleichung der Mechanik) vorliegen, die die Masse immer wieder zur Ruhelage zurückbewegt. Diese Kraft wird Rückstellkraft F_R genannt.

Diese Kraft soll anhand des Federpendels genauer betrachtet werden. Zur Betrachtung soll

folgende Abbildung dienen:

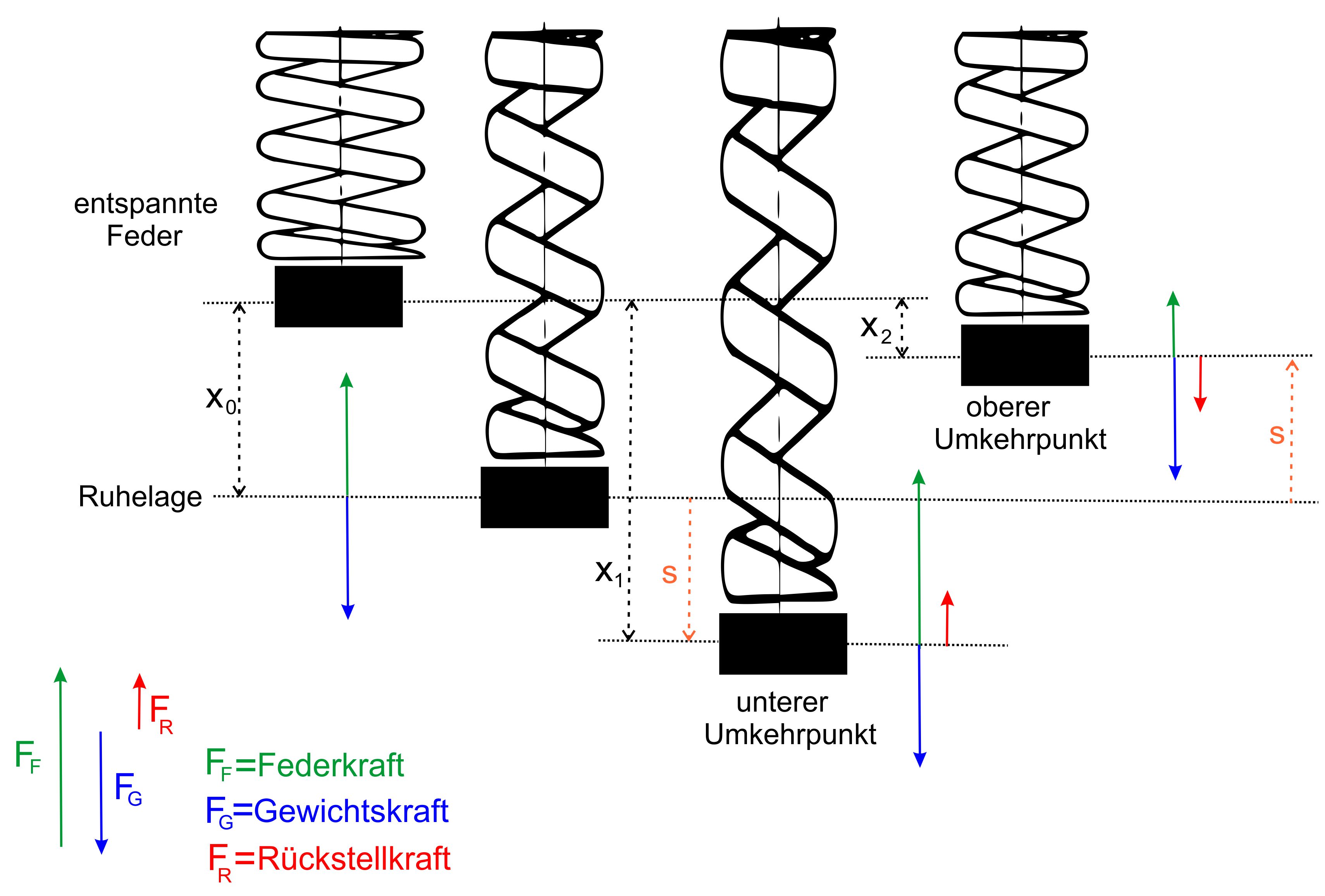
Erläuterung:

Da die Feder bei der Schwingung immer gedehnt ist, muss immer eine Federkraft auftreten.

Diese lässt sich mit dem Hookeschen Gesetz (s. dort) bestimmen.

Die Berechnung lautet F = D * s , in unserem Fall wählen wir statt „s“ den Buchstaben „x“, damit keine Verwechslung mit der Elongation stattfindet. In der Ruhelage also F₀ = D*x₀ , am unteren Umkehrpunkt F₁ = D * x₁ , am oberen Umkehrpunkt F₂ = D*x₂ .

Da x₂ < x₀ < x₁ gilt, ergibt sich für die Federkraft F₂ < F₀ < F₁ .

Gleichzeitig wirkt immer die Gewichtskraft der angehängten Masse m, die immer gleich groß ist, da gilt F_G = m*g.

Diese beiden Kräfte wirken gegeneinander und heben sich zum Teil auf. Die resultierende Kraft aus beiden Kräften ist dann die Rückstellkraft F_R .

Zusammenfassung:

Definition: Harmonische Schwingung

Eine harmonische Schwingung liegt vor, wenn die Rückstellkraft proportional zur Elongation ist, d.h. wenn gilt

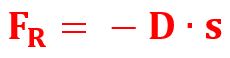
D = Richtgröße

D ist die Proportionalitätskonstante und wird Richtgröße genannt. Sie stimmt nur beim Fadenpendel mit der Federkonstanten überein. Bei anderen harmonischen Schwingungen muss D neu bestimmt werden (s. unten, Fadenpendel).

Beispielaufgabe

1. Berechnung einfacher Größen

Wenn man an eine Feder eine Masse m von 500 g hängt, wird die Feder um 40 cm gedehnt.

Anschließend wird bei eingehängter Masse m die Feder um weitere 30 cm gedehnt und dann losgelassen. Die Feder übt jetzt harmonische Federschwindungen aus.

Wie groß ist die größte Rückstellkraft? Wie groß sind die einzelnen Kräfte (Federkraft, Gewichtskraft, Rückstellkraft) bei einer Gesamtauslenkung der Feder von 60 cm? Welche Beschleunigung weist die Masse m dann auf?

Link zum Hookeschen Gesetz

Ausblick: Fadenpendel

Bisher haben wir fast ausschließlich das Federpendel betrachtet. Wie sieht es denn beim Fadenpendel aus? Handelt es sich hier um eine harmonische Schwingung?

Nach unseren Erkenntnissen ( s.oben ) müssen wir dazu kontrollieren, ob die Rückstellkraft proportional zur Elongation ist. Schauen wir uns dazu einmal die folgende Abbildung an.

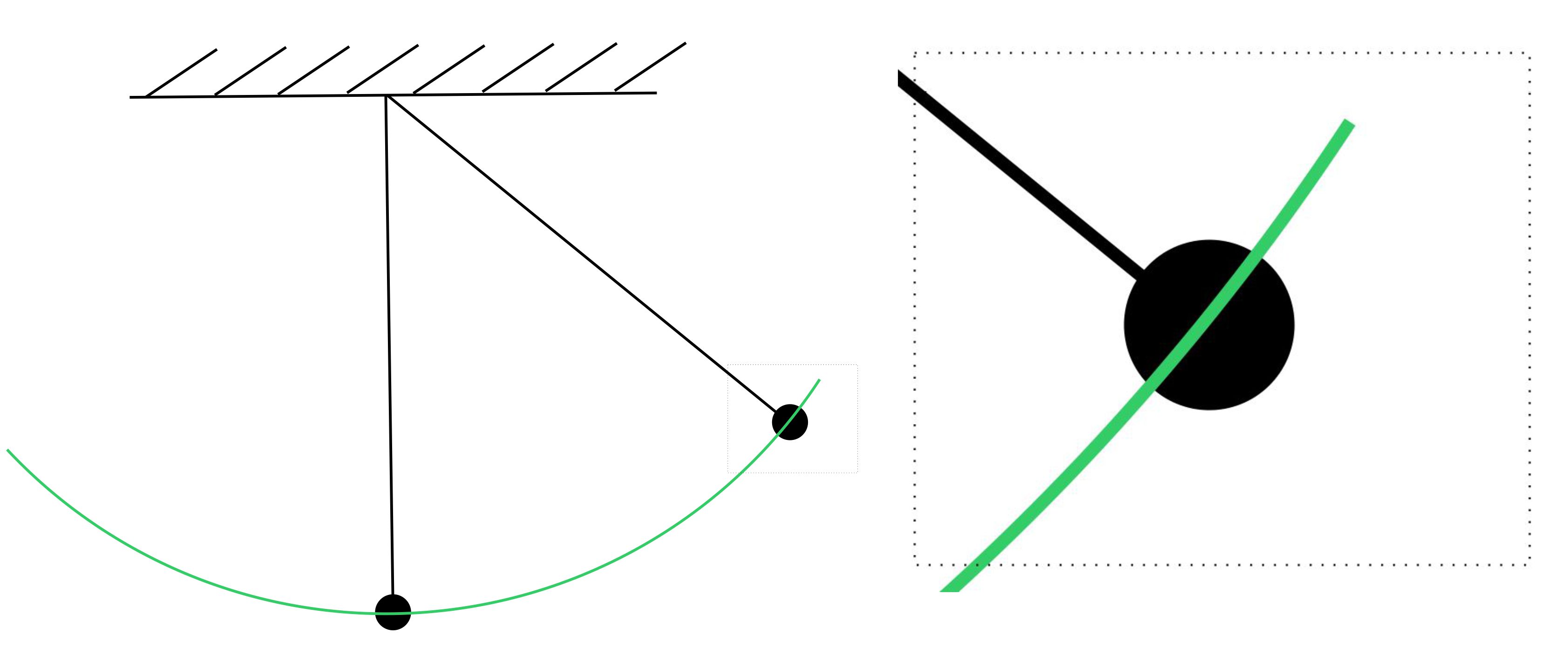
In welche Richtung zeigt die Rückstellkraft? Die Kraft zeigt immer in Richtung der Elongation. Die Elongation entspricht aber (s. oben) der Kreisbogenlänge. Wohin „zeigt“ die Kreisbogenlänge im rechten Punkt? Hierzu vergrößern wir einmal die Umgebung um den Punkt (s. Kreisbewegung). Dann sieht man in der rechten Abbildung, dass die Krümmung des Kreisbogens immer geradliniger wird und schließlich der Tangente an den Kreis entspricht, also zeigt die Rückstellkraft tangential zum Kreisbogen.

Woher stammt die Rückstellkraft? Es liegt nur eine Kraft vor, nämlich die Gewichtskraft. Diese hat aber Auswirkungen in Bewegungsrichtung. Man muss eine Komponentenzerlegung der Gewichtskraft vornehmen, d.h. ein Kräfteparallelogramm zeichnen, wobei die eine Richtung, eben die gesuchte, also die Tangente ist. Die andere Richtung steht dann senkrecht zu dieser Richtung, somit in Verlängerung des Fadens.

Folgende Abbildung zeigt die Gegebenheiten.

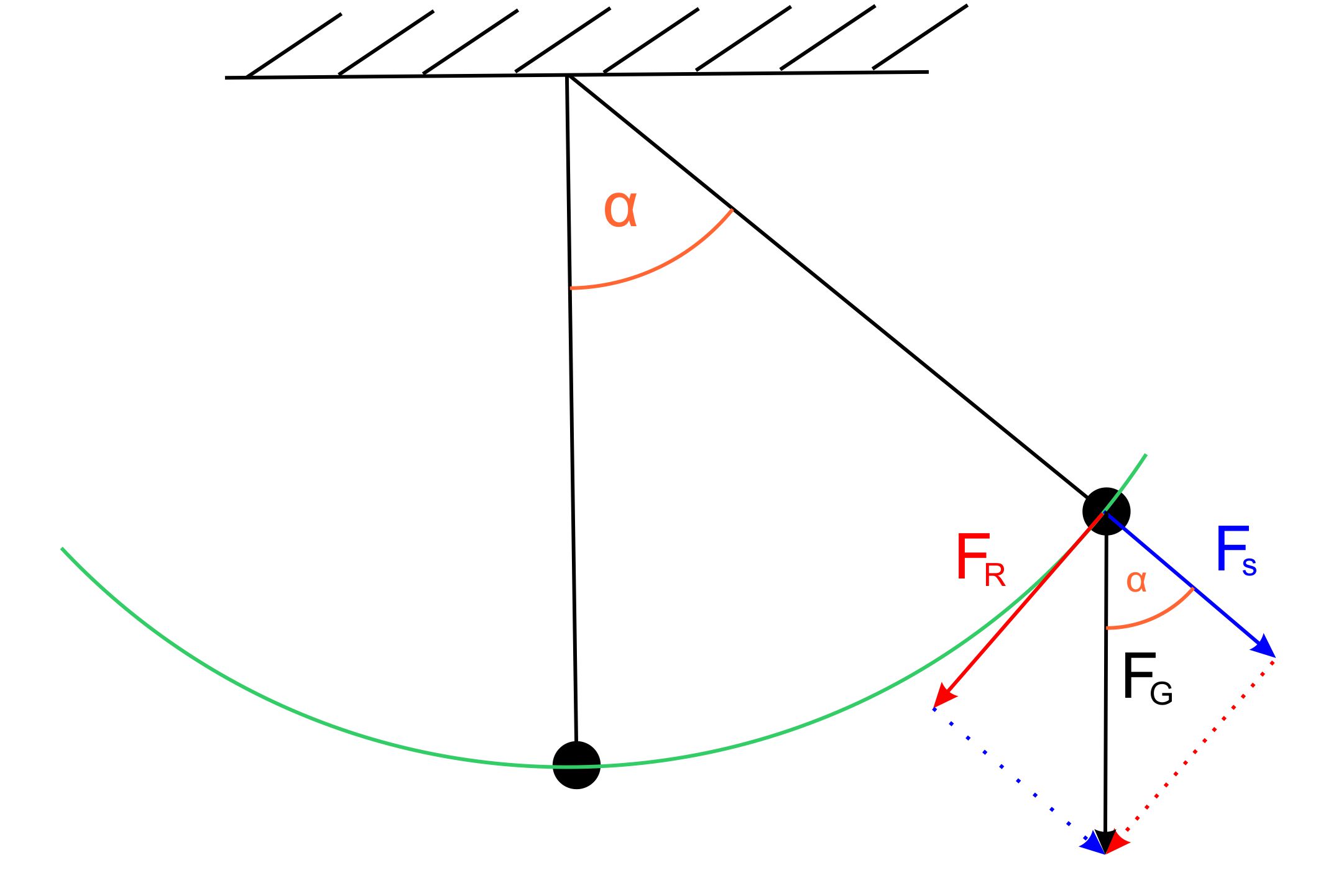
Man erkennt schnell aufgrund von Parallelitäten, dass der Auslenkwinkel α sich im Kräfteparallelogramm wiederfindet.

Es gilt somit:

Bewegungsgleichung – Schwingungsdauer

Das folgende Kapitel soll sich mit der Bewegungsgleichung und der Formel für die Schwingungsdauer beschäftigen. Die Bewegungsgleichung (s. Bewegungen) gibt den Zusammenhang zwischen der Elongation und der Zeit an, also s(t). Häufig interessiert man sich bei den Schwingungen noch mehr für die Schwingungsdauer (z.B. Pendeluhr). Daher ist es wichtig hier eine Formel aufzustellen, mit der man aus einfachen Vorgaben, die Schwingungsdauer T bestimmen kann. Da die Herleitungen sehr von den mathematischen Vorkenntnissen abhängen, wird im Folgenden je nach Jahrgangsstufe unterschiedlich vorgegangen.

1. Fall: Einführungsphase (hier nur die Herleitung der Schwingungsdauer)

2. Fall: Grundkurs Q1 und Leistungskurs Q1 (Herleitung Bewegungsgleichung und Schwingungsdauer)