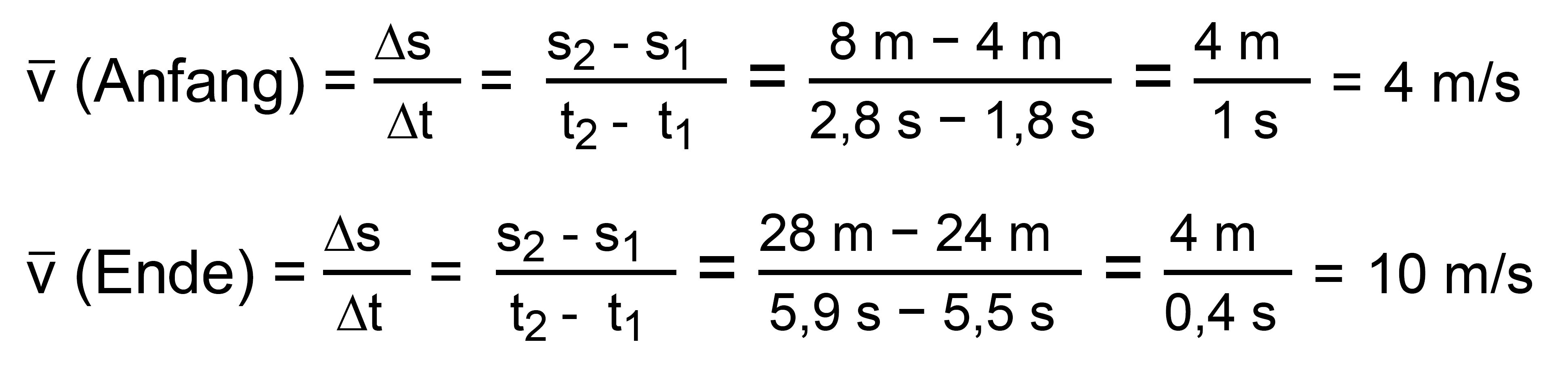|
Kinematik Beschreibung von Bewegungen Es
gibt verschiedene Möglichkeiten Bewegungen zu beschreiben. Nehmen
wir zum Beispiel eine Tachoscheibe.
Quelle:
wikipedia Auf
einer solchen Scheibe werden verschiedene Werte registriert. Man
sieht, zu welcher Zeit (am Rand) der Fahrer welche Geschwin- digkeit (Mitte)
gefahren ist. Es werden also die Werte "Zeit" und "Ge- schwindigkeit"
aufgenommen. Im
Allgemeinen hat man bei Bewegungen aber häufig das Problem, dass
kein "Tachometer" vorhanden ist, mit dem man Geschwindig- keiten messen
kann. Dann wird man im einfachsten Fall den zurück- gelegten
Weg in Abhängigkeit von der Zeit messen. Man fertigt da- nach
zur Auswertung sogenannte t-s−Diagramme an. In einem t- s−Diagramm
wird auf der Abszisse (x-Achse) die Zeit und auf der Ordinate
(y-Achse) der dazu gehörige zurückgelegte Weg (vom Start ausgehend)
aufgetragen. Der Graph dieser Diagramme macht dann Aussagen
über die Art der Bewegung. Beispiel der
Untersuchung einer Bewegung: Anfahren eines
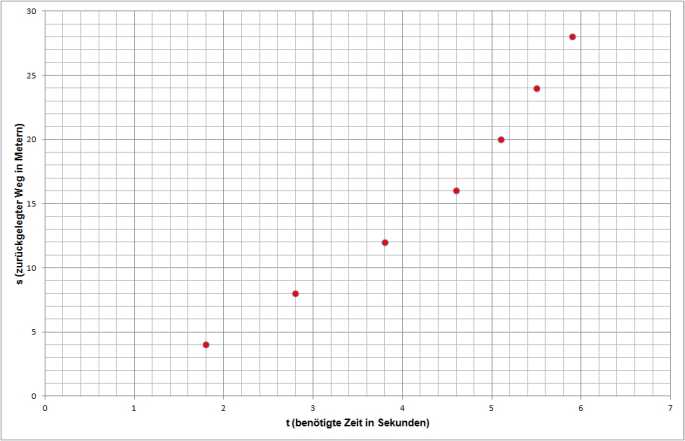
Fahrradfahrers Es werden folgende Messwerte aufgenommen:
Diese
Messwerte werden in einem t-s-Diagramm dargestellt (am
ein- fachsten
mit einer Tabellenkalkulation (z.B. Excel))
Aus
diesem Diagramm werden jetzt verschiedene Schlussfolger- ungen über
die Bewegung gezogen. Zum Beispiel sieht man sofort, dass
es sich um eine beschleunigte Bewegung handeln muss, da am
Schluss mehr Strecke in dem gleichen Zeitintervall zurückgelegt wird
als am Anfang, d.h. die Geschwindigkeit hat zugenommen. Wie
bestimmt sich jetzt aber die Geschwindigkeit genau? In diesem Fall
kann man zunächst nur Durchschnittsgeschwindigkeiten be- stimmen. Es
wird dabei festgelegt:
Es
ergibt sich somit die Einheit:
Konkret
heißt dies jetzt für den obigen Fall: Wollen
wir die Durchschnittsgeschwindigkeit am Anfang und am Ende
bestimmen, müssen wir uns ein Zeitintervall am Anfang und am
Ende wählen und die in diesem Zeitintervall zurückgelegte Strecke
wählen. Also z. Bsp. Anfang: Zeitintervall von 1,8 s bis 2,8 s mit
der Strecke 4 m; Ende: Zeitintervall von 5,5 s bis 5,9 s mit eben- falls
4 m. Es
ergibt sich somit:
Eine
Umrechnung in die im Alltag häufige Einheit km/h ist recht einfach. Es
gilt nämlich:
|