|
Schwingungsdauer – E-Phase Zunächst einmal schauen wir uns die
Projektion einer Kreisbewegung an und klären den Zusammenhang zur
harmonischen Schwingung. Projektion bedeutet, dass man sich den
Schattenwurf einer gleich- förmigen Kreisbewegung ansieht. Hierzu gibt es ein nettes Video, welches auch
schon zeigt, dass der Schattenwurf, also die Projektion, etwas mit der
harmonischen Schwin- gung zu tun hat. Quelle: https://www.youtube.com/watch?v=ZZiE8KbkTuw An folgender Abbildung soll dies mathematisch
exakt geklärt werden:
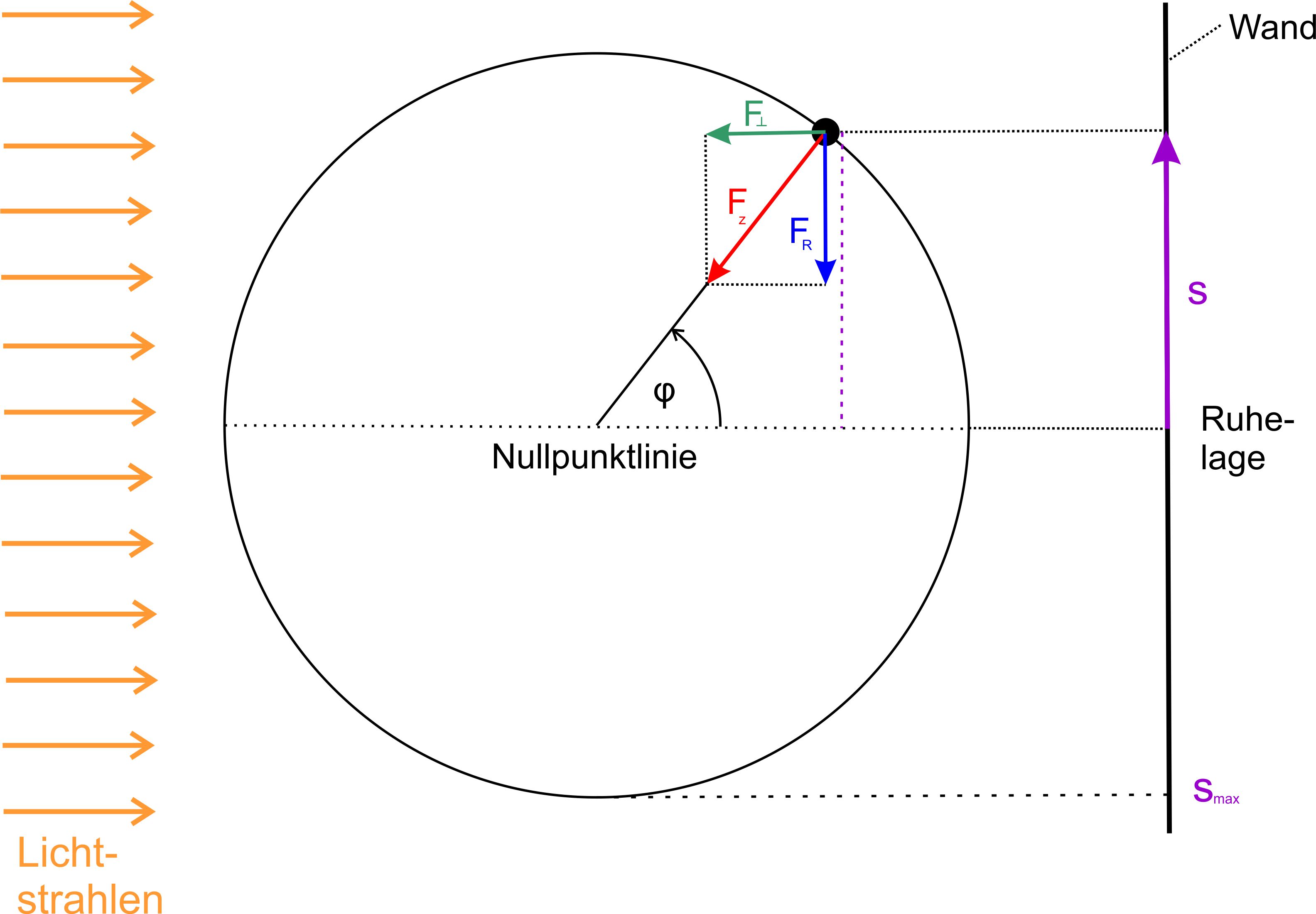
In der Mitte befindet sich eine Masse, die
sich gleichförmig auf einer Kreisbahn bewegt. Diese Kreisbewegung wird
von links mit parallelem Licht bestrahlt, so dass an der Wand ein
Schattenwurf (eine Projektion) der Kreisbewegung zu sehen ist. Die Frage
ist, ob die Bewegung des Schattenpunktes eine harmonische Schwingung
darstellt. Zur Erinnerung: (s. harmonische Schwingung) Eine harmonische Schwingung liegt vor, wenn
die Rückstellkraft propor- tional zur Elongation ist,
d.h. FR = - D · s gilt. Wir müssen also zeigen, dass dieser
Zusammenhang besteht. Was ist aber die Rückstellkraft im Schattenwurf. Dies
ist natürlich die Kraftkom ponente der Zentripetalkraft
FZ , die als Schattenwurf auf die Wand projiziert wird. In der Abbildung ist das die
blaue Kraftkomponente. Es gilt nun Folgendes:
Zunächst wurde jetzt gezeigt, dass die
Projektion einer gleichförmigen Kreisbewegung eine harmonische Schwingung
ist. Wie hilft uns dies weiter, um eine Formel für die
Schwingungsdauer zu gewinnen? Dazu stellen wir uns einmal vor, die Masse
würde einen vollständigen Kreis umlaufen, wobei wir die Uhr starten,
wenn die Masse sich auf der Nullpunktslinie, also in der Projektion in
der Ruhelage, befindet. Wenn die Masse einen vollständigen Kreis
beschreibt, ist in der Projektion, also bei der harmonischen Schwingung, eine
vollständige Schwingung ablaufen. Dies bedeutet, dass die Umlaufdauer
des Kreises der Schwin- gungsdauer entspricht. Wir können
unser Wissen über gleichförmige
Kreisbewegungen dazu nutzen die Schwingungsdauer auszurechnen. Es ergibt sich Folgendes:
Zusammenfassend ergibt sich also:
Schwingungsdauer: Federpendel und
Fadenpendel Die häufigsten harmonischen Schwingungen sind die
Schwingung des Federpendels und des Fadenpendels (bei
kleinem Auslenkungs- winkel).
Hier kennen wir auch die Richtgröße D. Es gilt:
Bewegungsgleichung Um zur
Bewegungsgleichung zu kommen, gehen wir noch einmal zur Herleitung
der Rückstellkraft zurück. Hier steht eine Formel für s(t), mit der wir
weiterarbeiten können.
Somit gilt
also Folgendes für die Bewegungsgleichung:
- zurück zur „Harmonischen Schwingung“ - weiter zur „Energie
einer harmonischen Schwingung“ |