|
Zusatzaufgaben 1.
Bungee-Sprung ( sehr schwer) Vorweg-Kommentar: Eine Aufgabe, die eine Zeit lang im
Fokus der Öffentlichkeit stand, war die Aufgabe zum Bungee-Sprung. Diese Aufgabe wurde in der
Presse angepriesen als die Aufgabe, die endlich einmal den Anwendungsbezug zum
Alltag der Schüler herstellt. Für Schüler wäre der Physik-Unterricht nur interessant,
wenn diese Aufgabe im Unterricht behandelt würde. Verkannt wurde dabei völlig, dass diese
Aufgabe extrem viel voraussetzt und damit extrem schwierig ist. Video eines Bungee-Sprungs: Hier eine mögliche Aufgabenstellung: Ein Bungeespringer mit
einer Masse von 70 kg springt aus einer Höhe von 60 m über dem
Erdboden ab. Er hängt an einem Seil der Länge 25 m. Wenn er am Ende
des Sprungs zum Stillstand kommt, befindet er sich 30,4 m über dem
Erdboden. Vor dem Stillstand bewegt er sich periodisch auf und ab.
a.) Bestimmen Sie die
Schwingungsdauer T des Sprunges. Hinweis: Man soll von
einer harmonischen
Schwingung ausgehen und das Hookesche Gesetz soll gelten. b.) Berechnen Sie die
maximale Geschwindigkeit des Springers. c.) Wie weit wird das
Seil maximal ausgedehnt? d.) Welchen Wert hat die
größte Beschleunigung? Hinweis: Um diese Aufgabe
zu lösen, müssen viele Einschränkungen (neben den Bedin- gungen
unter a.))
in Kauf genommen werden, nämlich - der Sprung erfolgt
reibungsfrei - die Person bildet
einen Massepunkt, d.h. die Körpergröße spielt keine Rolle - die Person fällt
geradlinig herunter und führt keine Drehbewegungen aus Lösung: Die Lösung ist nur
unter folgenden Voraussetzungen möglich: Man muss die
Themenbereiche „Energie“, „Energieerhaltungssatz“, „Hookesches Gesetz“,
„Harmonische
Schwingungen“, „Schwingungsdauer
einer harmonischen Schwingung“ und „Grundgleichung
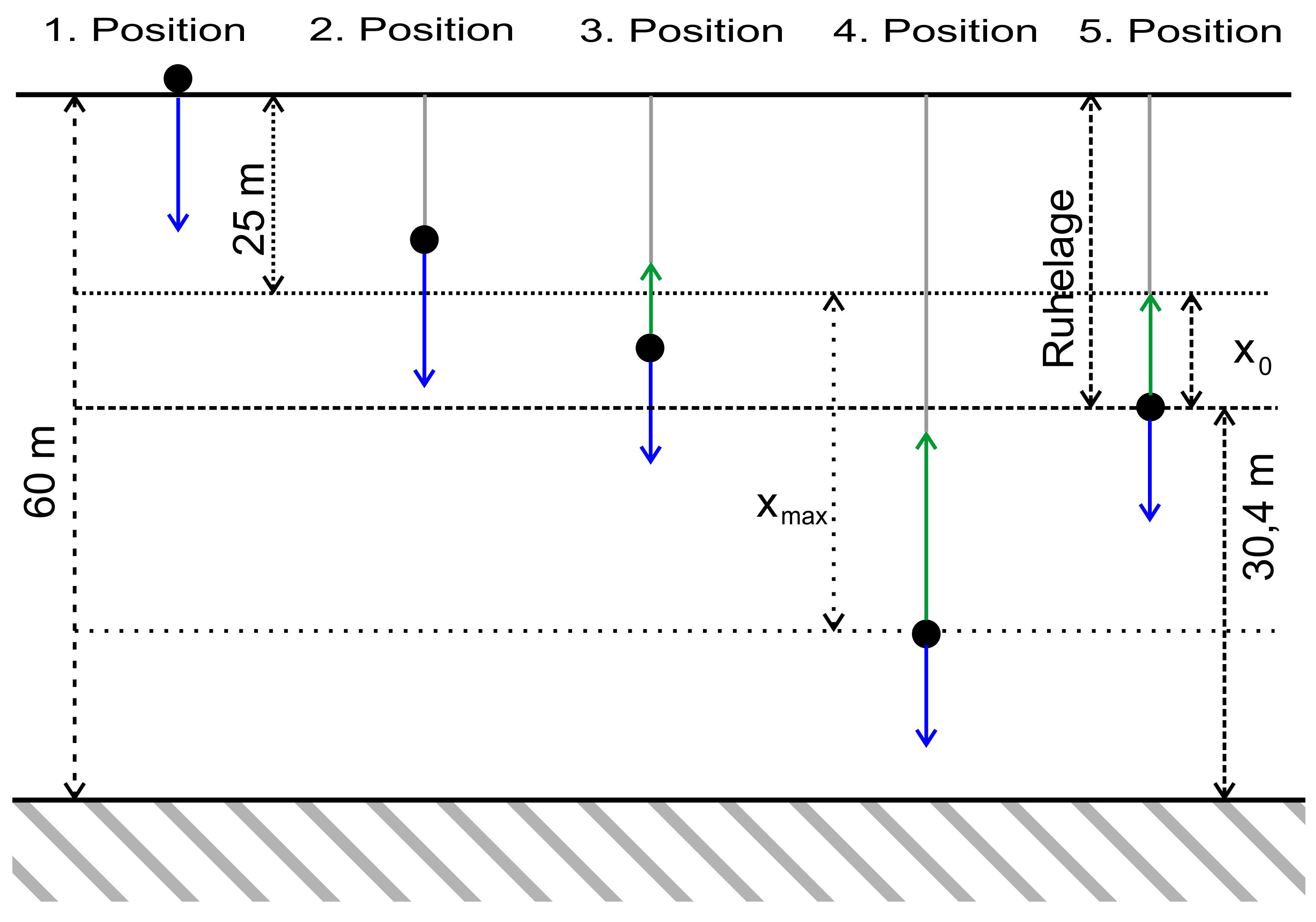
der Mechanik“ bearbeitet haben. Zunächst schauen wir
uns die Kräfte- und Energieverhältnisse in einer Abbildung an.
Kräfteverhältnisse: An jeder Position
wirkt natürlich die Gewichtskraft (blau). Diese be- stimmt sich mit FG = m ∙ g. Sobald das Seil gespannt
wird, also ab einer Fallhöhe von 25 m (Seil- länge) kommt die
Federkraft (s.
Hookesches Gesetz) dazu. Die Feder- kraft wirkt der
Ausdehnung entgegen. Es gilt: FF = D ∙ x (x = Ausdehnung, D = Federkonstante). Im unteren
Umkehrpunkt liegt die größte Federkraft vor. In der Ruhelage (s.
harmonische Schwingungen) gleichen sich die bei- den
Kräfte aus. Es
gilt dann: FG
= FF also m ∙ g =
D ∙ x0. Wird über die Ruhelage hinaus
gespannt, wirkt die resultierende Kraft nach oben. Bis zur Ruhelage wirkt die
resultierende Kraft nach unten, d.h. es findet eine Beschleunigung des Körpers statt.
Nach der Ruhelage wird der Körper abgebremst. Energieverhältnisse: ( s. Energieformen) Am Start liegt nur potentielle Energie
vor. Sie bestimmt sich mit Epot = m ∙ g ∙ h. Sobald der Körper fällt, tritt wegen
der Geschwindigkeit kinetische Energie auf. Es gilt: Ekin
= ½ ∙ m ∙ v2. Sobald sich die Feder spannt, liegt
Spannenergie vor, die sich berech- net mit Espann = ½ ∙ D ∙
x2 Kommen wir jetzt zur Lösung der
einzelnen Aufgaben.
Zusatzmaterial:
|