|
Besondere Arbeitsformen Spannarbeit - Hookesches Gesetz
Im Folgenden geht es um die Eigenschaften von
Schraubenfedern, also um Federn, die eine Schraubenform haben. Federn ausdehnt oder zusammendrückt, muss man
eine Kraft auf- bringen, da jeder Feder versucht in ihren
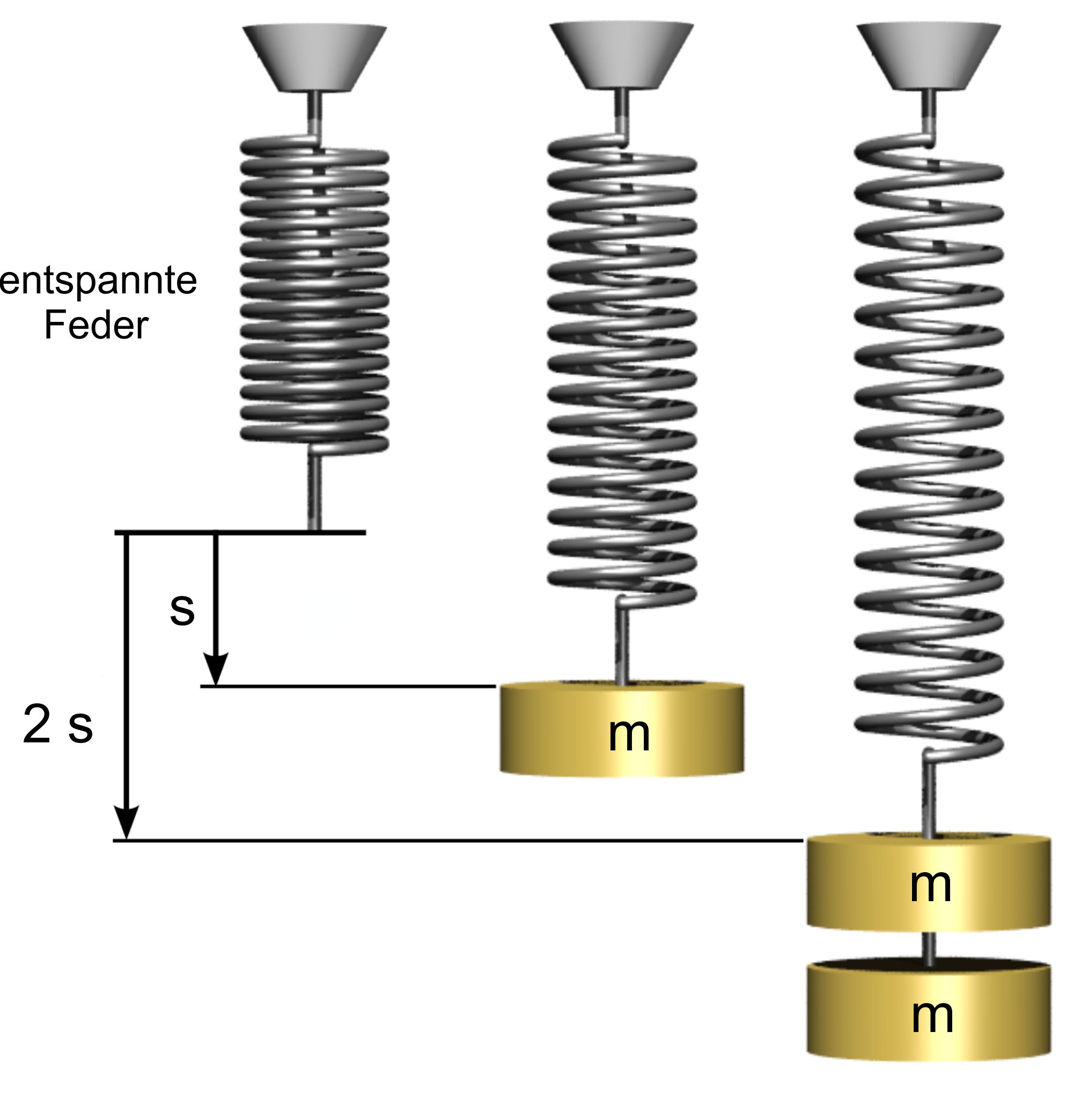
entspannten Zustand zurück- zukehren, solange sie elastisch ist. geübt wird, um wieder in den entspannten
Zustand zurückzukehren, nennen wir Federrückstellkraft oder einfach
Federkraft. Gegen diese Kraft muss man anarbeiten, um die Feder
auszudehnen bzw. zusam- menzudrücken. Zunächst einmal wollen wir herausfinden, wie
man die Federkraft be- rechnet. Hookesches Gesetz Das
Hookesche Gesetz beschreibt den Zusammenhang zwischen der Ausdehnung
der Feder s und der Federkraft F. bei der Abstand
zwischen entspanntem Zustand und ausgedehntem Zustand. Das
Hookesche Gesetz besagt nichts anderes, als dass eine Pro- portionalität zwischen
Federkraft und Ausdehnung vorliegt. Dies wird an folgender
Abbildung noch einmal veranschaulicht.
Quelle:https://upload.wikimedia.org/wikipedia/commons/f/fc/Hookes-law-springs.png?uselang=de (
leicht geändert) Ein sehr schönes Video, in dem auch
Experimente durchgeführt werden, findet sich hier: Wie man dem Video entnehmen kann,
ergibt bei einem Auftrag der Federkraft F gegen die Ausdehnung
s im Idealfall eine Ursprungs- gerade. (Hinweis: Im Video wird die
Federkraft nicht direkt gemessen, sondern die Feder durch die Gewichtskraft gespannt. Nach dem
Anhängen der Massestücke stellt sich ein Kräftegleich- gewicht zwischen
der ausdehnenden Gewichtskraft und der zurückziehenden Federkraft ein, so dass man mittels der
Gewichtskraft die Federkraft bestimmen kann) Da die Messwerte immer mit
Messfehlern behaftet sind (z. Bsp. durch Ablesefehler, Rundungsfehler
usw.) zieht man eine Gerade, die im Idealfall auf- treten würde. Diese Gerade nennt
man Ausgleichsgerade. In einer Tabellenkalkulation wird von der
Trendlinie gesprochen. sieht also der Zusammenhang
folgendermaßen aus: In der Abbildung sind zwei elastische Federn
aufgetragen. Beide Ab- hängigkeiten lassen sich über
eine Ursprungsgerade beschreiben, also gilt als Funktionsterm F = k ∙ s, wobei
k die Steigung der Geraden ist. Je steiler die Gerade ist, um so schwerer ist es, die Feder auszu- dehnen. Man sagt auch: die Feder ist härter.
Die Steigung der Gera- den ist also ein Maß für die Härte der Feder.
Deshalb wird die Steigung bzw. die Proportionalitätskonstante auch
Federhärte (bzw. Feder- konstante) genannt. Die Federhärte wird mit
dem Buchstaben D ange- geben. In unserem Fall ist also Drot
= 40 N/m und Dblau = 60 N/m. Wir fassen zusammen:
Beispielaufgabe (einfache) Umstellung
der Formel nach der gesuchten Größe a.)
Durch das Anhängen einer Masse von 400 g wird eine Feder um 20 cm
ausgedehnt.
b.) Man
hängt an eine Feder der Federhärte D = 25 N/m
eine Masse von 600 g. Berechnen Sie die Größe der Ausdehnung.
|