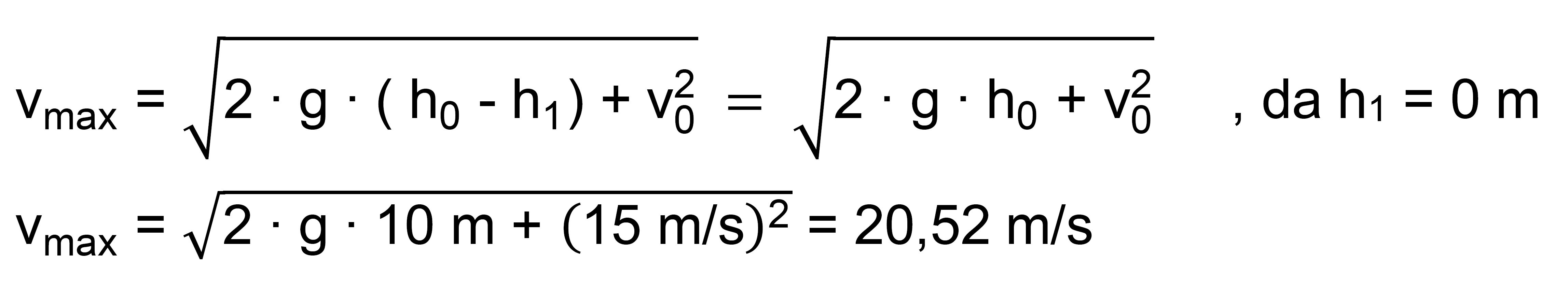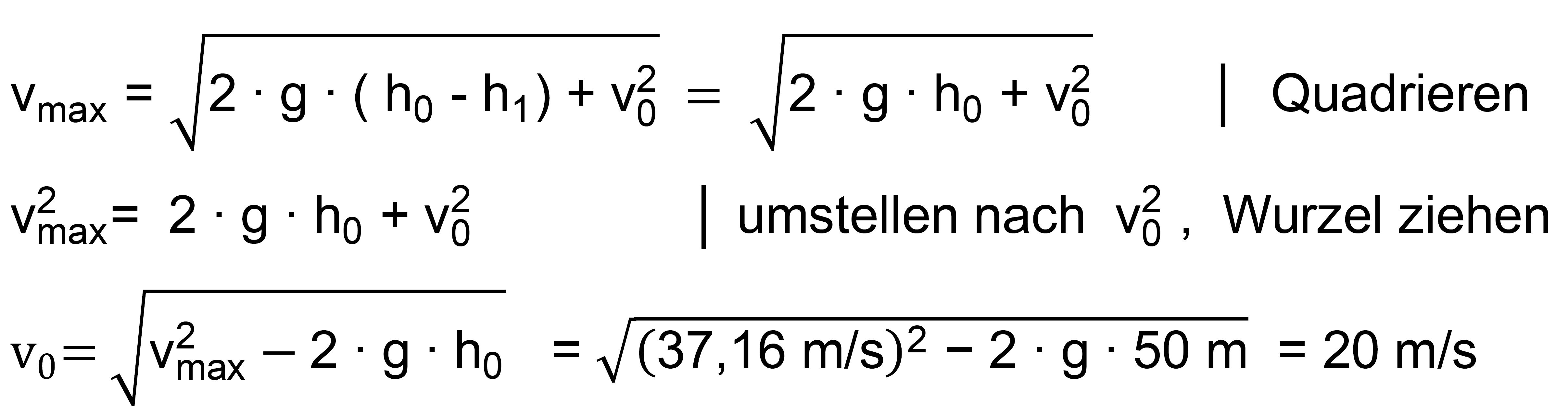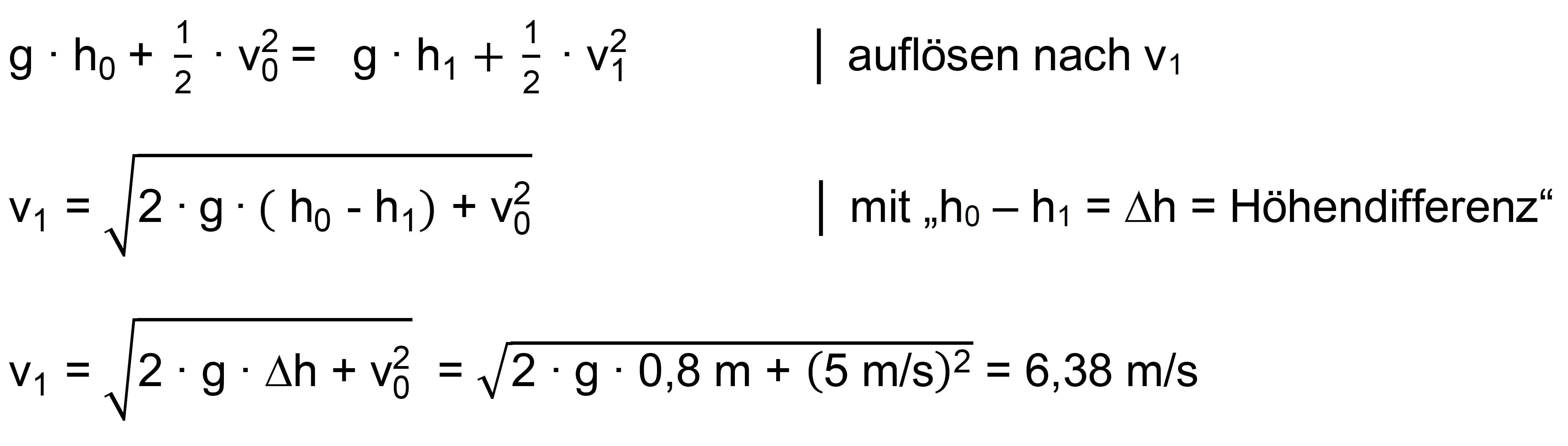|
Energieerhaltung
– Übungsaufgaben 1. Übungsaufgabe: lotrechter Wurf (einfach,mittel) 2. Übungsaufgabe: schiefer Wurf (einfach,
mittel) 3. Übungsaufgabe: Schaukel (einfach, mittel) 1.
Übungsaufgabe Ein Körper wird aus einer Höhe von 10 m lotrecht nach
oben geworfen. Er weist dabei eine Abwurfgeschwindigkeit von 15 m/s
auf. a.) Welche maximale Höhe erreicht der Körper? b.) In welcher Höhe hat er eine Geschwindigkeit von 10
m/s (20 m/s; 30 m/s)? c.) Berechne die Geschwindigkeit in einer Höhe von 18 m
(25m). a.) Im höchsten Punkt ist die Geschwindigkeit v1 = 0 m/s. Die „Grundgleichung“ vereinfacht sich.
Link: Lotrechter Wurf zu b.) Vollständige „Grundgleichung“ wählen und umstellen nach h1 (s. Formel)
Was bedeutet dies jetzt? 16,37 m liegt höher als die Starthöhe, also ist kinetische Energie in
potentielle Energie umgeformt worden. Die Geschwindigkeit ist kleiner als die
Abwurfgeschwindigkeit. 20 m/s ist größer als die Abwurfgeschwindigkeit, also muss potentielle
Energie in kinetische Energie umgewandelt worden sein. Die Höhe muss unter der Abwurfhöhe liegen. 30 m/s ergibt einen negativen Wert. Die Geschwindigkeit ist nicht
möglich, weil man sich unterhalb der Erdoberfläche befindet. Hinweis: Die maximale Geschwindigkeit erhält man für h1 = 0
m (Erdoberfläche). Dann ist die gesamte potentielle Energie in kinetische Energie übergegangen. Man kann die Formel aus der Grundgleichung benutzen.
zu c.) Gleiche Formel wie bei b.) unter dem Hinweis benutzen, also
für h1 = 18 m musste kinetische Energie in potentielle
Energie übergehen für h1 = 25 m ergibt sich keine Lösung (Radikand ist
negativ), die liegt daran, dass man nicht genug kinetische Energie hat, um diese Höhe zu
erreichen. In a.) wurde die maximale Höhe mit 21,47 m berechnet. Hinweis: Man kann die Aufgaben natürlich
auch mittels der Bewegungsgleichungen (s.
Lotrechter Wurf) lösen. Dazu muss man aber immer als Zwischenergebnis
Zeiten bestimmen, was deutlich umständlicher wäre. Dafür würde man merken,
dass man für die Höhen (s.c.) zwei Zeiten und somit
zwei Geschwindigkeiten (+8,25 m/s und – 8,25 m/s) erhält, da der Körper die
Höhe (größer als 10 m) zweimal durchläuft. Mit dem Energieerhaltungssatz kann
man nichts über die Bewegungsrichtung aussagen, sondern nur über den Betrag
der Geschwindigkeit. Ein Körper
wird mit der Geschwindigkeit v0 aus einer Höhe h0 von
50 m abgeworfen.
Beim Aufprall hat er eine Geschwindigkeit von 37,16 m/s. Welche
Abwurfgeschwindigkeit hatte der Körper? Lösung: Grundgleichung wählen und nach v0 umstellen.
Ein Kind
wird in einer Schaukel um 80 cm gehoben und dann a.) einfach
losgelassen b.) mit
einer Geschwindigkeit von 5 m/s angestoßen Wie groß
ist die Geschwindigkeit am tiefsten Punkt der Schaukel? Lösung: Zur Lösung wird wieder die „Grundgleichung“ benutzt. Gesucht ist v1. Gegeben sind h0 und v0. Im tiefsten Punkt liegt die maximale Geschwindigkeit vor, da die potentielle Energie am geringsten ist. zu a.)
zu b.) Die Grundgleichung muss vollständig benutzt werden und nach v1 aufge- löst werden (s.Formeln)
1. Übungsaufgabe: lotrechter Wurf (einfach,mittel) 2. Übungsaufgabe: schiefer Wurf (einfach, mittel) 3. Übungsaufgabe: Schaukel (einfach, mittel) |