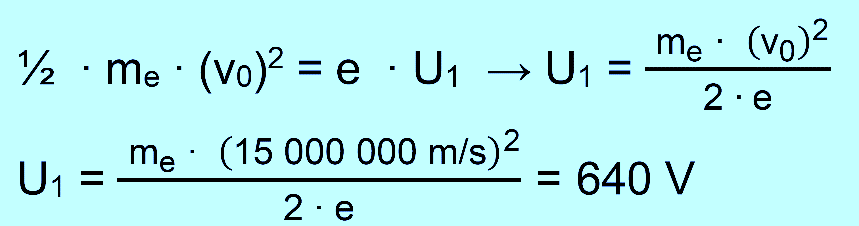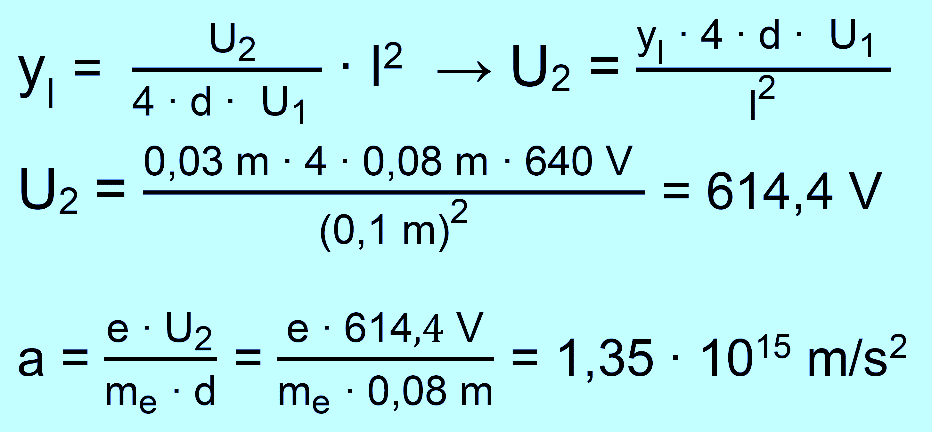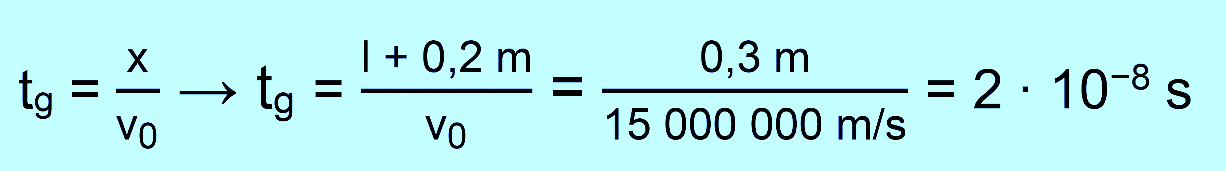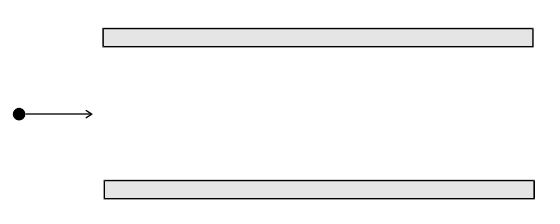
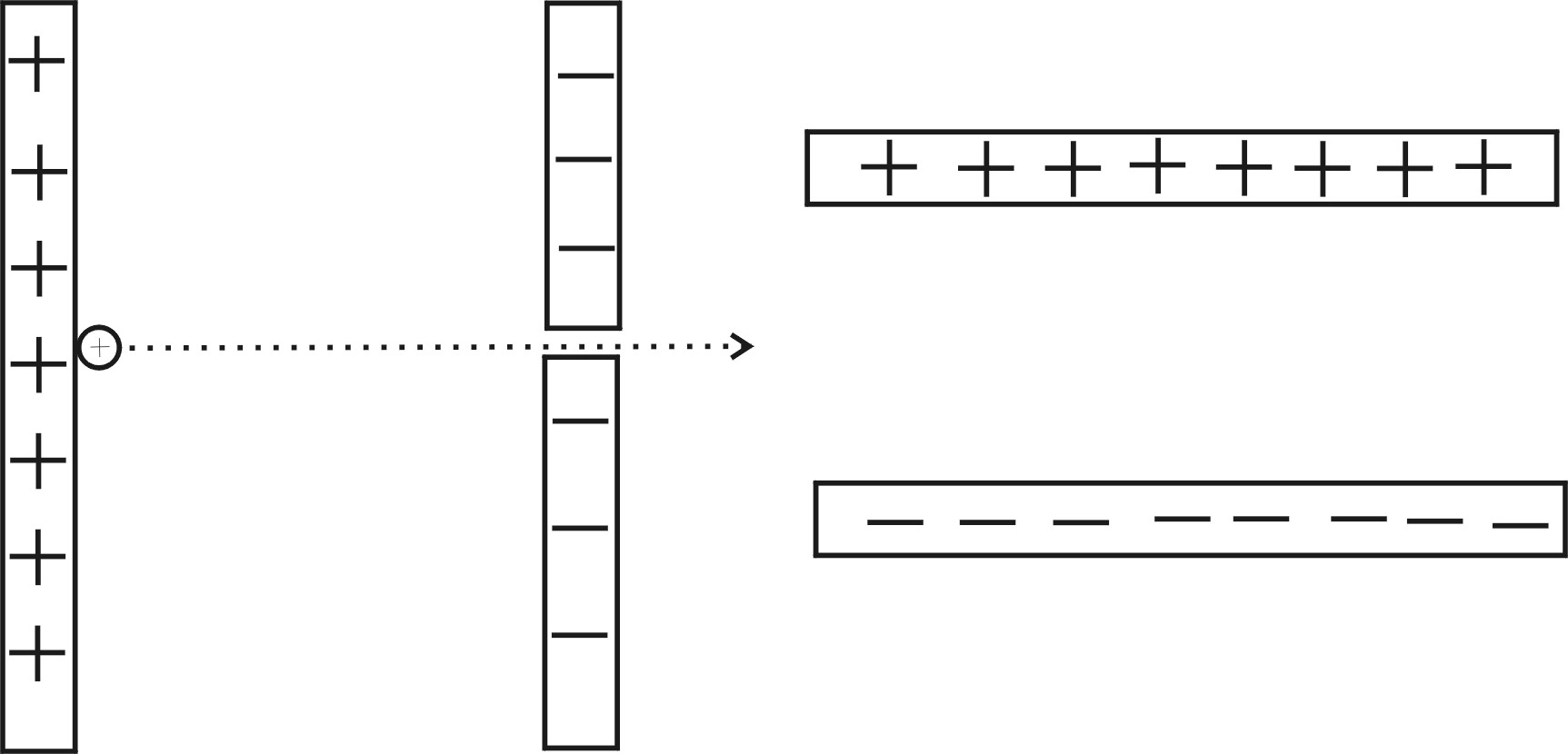
Klausuraufgaben-Ablenkkondensator

Aufgabe Nr.1

In das elektrische Feld eines Plattenkondensators tritt mittig (s.Abb.)

ein Elektron mit der Geschwindigkeit v₀ = 15 000 000 m/s ein.

Beantworten Sie folgende Fragen:

a.) Mit welcher Beschleunigungsspannung U₁ ist das Elektron aus

der Ruhe auf die Geschwindigkeit v₀ gebracht worden?

b.) U₁ sei 640 V. Die Ablenkplatten haben einen Abstand von 8 cm.

Wie groß muss die angelegte Ablenkspannung U₂ sein, damit das

Elektron am Ausgang des 10 cm langen Kondensators eine Ab-

lenkung in y-Richtung von 3 cm erfahren hat? Welche Beschleu-

nigung hat auf das Elektron dann eingewirkt?

c.) Beim Eintritt in den Ablenkkondensator startet eine Uhr ( t = 0 s ).

Welche Zeit braucht das Elektron, um auf einen Schirm aufzutref-

fen, der 20 cm vom Ende des Ablenkkondensators entfernt steht?

( U₁ = 640 V, U₂ = 615 V)

d.) U₂ sei jetzt 500 V. Unter welchem Winkel verlässt das Elektron

in diesem Fall den Kondensator? Welche Geschwindigkeit weist es

beim Verlassen des Kondensators auf ?

Lösung:

Zur Lösung werden die Formeln aus den Kapiteln „Ablenkkonden-

sator“ und „Übungsaufgaben zum Ablenkkondensator“ benutzt.

a.)

Im Beschleunigungskondnesator gewinnt man die kinetische

Energie aus der vom elektrischen Feld verrichteten Arbeit.

b.)

Man benutzt die Formel für die Gesamtablenkung am Kondensator-

ende und stellt dies nach U₂ um. Zur Beschleunigung wird die

Formel aus dem Kapitel „Ablenkkondensator“ bei der Herleitung

von y_l benutzt.

c.)

Man benutzt das Superpositionsprinzip, d.h. dass die Bewegung in

x-Richtung unabhängig ist von der Bewegung in y-Richtung.

Für die Zeitberechnung kann man also die Zeit für die x-Bewegung

wählen.

d.)

Es müssen einige zusätzliche Größen berechnet werden, bevor man

den Winkel bestimmen kann. Für den Winkel gibt es zwei Formeln

mit tan(α), die beide benutzt werden. Am Schluss bestimmt man

v_g(l) mit der Vektoraddition.

y_s wird zunächst berechnet. Damit das Elektron auf dem Schirm

aufkommt, muss es natürlich den Kondensator verlassen, d.h.

y_l muss kleiner als 4 cm sein. Dies dürfte aber gegeben sein, da in

b.) für y_l = 3 cm die Spannung U₂ = 614,4 V vorliegt und man bei

d.) von einer geringeren Spannung ausgeht. Dies ist in der Rech-

nung aber noch einmal kontrolliert worden.

Aufgabe Nr.2

Im folgenden Aufbau wird zunächst eine kleine positive Kugel A im

Feld des linken Kondensators K₁ beschleunigt und gelangt danach

mittig in den rechten Kondensator K₂.

Der Abstand der Kondensatorplatten von K₁ beträgt 20 cm. Die Ge-

schwindigkeit des Kügelchens beträgt beim Austritt aus dem linken

Kondensators v = 10 954,45 m/s. Das Kügelchen weist eine Masse

von m = 5∙10⁻¹⁵ kg und eine Ladung von Q = 3∙10⁻¹⁰ As auf. Bei der

Bewegung braucht die Gewichtskraft nicht berücksichtigt werden.

a.)1.) Begründen Sie, warum A in K₁ eine gleichmäßig beschleu-nigte Bewegung ausführt.

2.) Bestimmen Sie von K₁: - die Spannung, die anliegt, - die Be-

schleunigung von A, - die Zeit, die A benötigt, um die rechte Platte

zu erreichen (Ausdehnung von A bleibt unberücksichtigt),

[ zur Kontrolle: t = 3,65∙10^-5 s; U = 1000 V ]

b.) Beschreiben Sie ausführlich die Bewegung, die A in diesem Kon-

densator K₂ ausführt, wenn

1.) keine Spannung anliegt

2.) wenn eine Spannung angelegt wird.

c.) Am Kondensator K₂ sei jetzt eine Spannung von 50 V angelegt.

K₂ sei 30 cm lang und der Plattenabstand betrage 10 cm. Zeigen

Sie, dass A den Kondensator K₂ verlassen kann, ohne auf einer der

Platten aufzutreffen.

Lösung:

a.)1.)

Im Kondensator liegt ein homogenes Feld vor, d.h. die Feldstärke

und somit die elektrische Feldkraft ist überall gleich groß. Wenn

F_E konstant ist, ist nach der Grundgleichung der Mechanik auch

„a“ konstant, d.h. es liegt eine gleichmäßig beschleunigte Bewegung

vor.

a.)2.)

Man benutzt den Energieerhaltungssatz, die Grundgleichung der

Mechanik und die Formeln für gleichmäßig beschleunigte Beweg-

ung.

b.)1.)

ohne Spannung:

wenn keine Spannung anliegt, findet keine Ablenkung statt und A bewegt sich einfach gleichförmig weiter mit v_x = v₀ .

b.)2.)

mit Spannung:

Es gilt das Superpositionsprinzip. Man hat eine gleichförmige

Bewegung in der Horizontalen und eine gleichmäßig beschleunigte

Bewegung in der Vertikalen [s. a.)1.)]. Man erhält als Bahnkurve

eine Parabel.

Es liegen ähnliche Verhältnisse wie beim waagerechten Wurf vor.

c.)

Man bestimmt die Ablenkung y_l am Ende des Kondensators. Wenn

diese kleiner ist als die Hälfte des Abstandes, kann A den Ablenk-

kondensator verlassen, weil A nicht vorher auf die Platten stößt.

y_l kann man auf zwei Weisen berechnen. Zur Kontrolle sind beide

Möglichkeiten durchgeführt. Im ersten Fall spielt die Größe der

Ladung und Masse von A keine Rolle.

- zu Aufgabe Nr.1 - Aufgabe Nr.2

- zurück zum Kapitel „Ablenkkondensator“

- zurück zu Übungsaufgaben „Ablenkkondensator“

- zurück zur Übersicht „Felder“