Schraubenbahn
− schräger Einschuss Bisher
haben wir die Elektronen immer senkrecht in das Magnetfeld eingeschossen
(s. Fadenstrahlrohr), so
dass eine Kreisbahn im Magnetfeld
auftrat. Was ist
jetzt, wenn die Elektronen schräg zu den Magnetfeldlinien ein- geschossen
werden? Dies soll in diesem Extra-Kapitel behandelt wer- den. Die
Situation sieht also folgendermaßen aus:
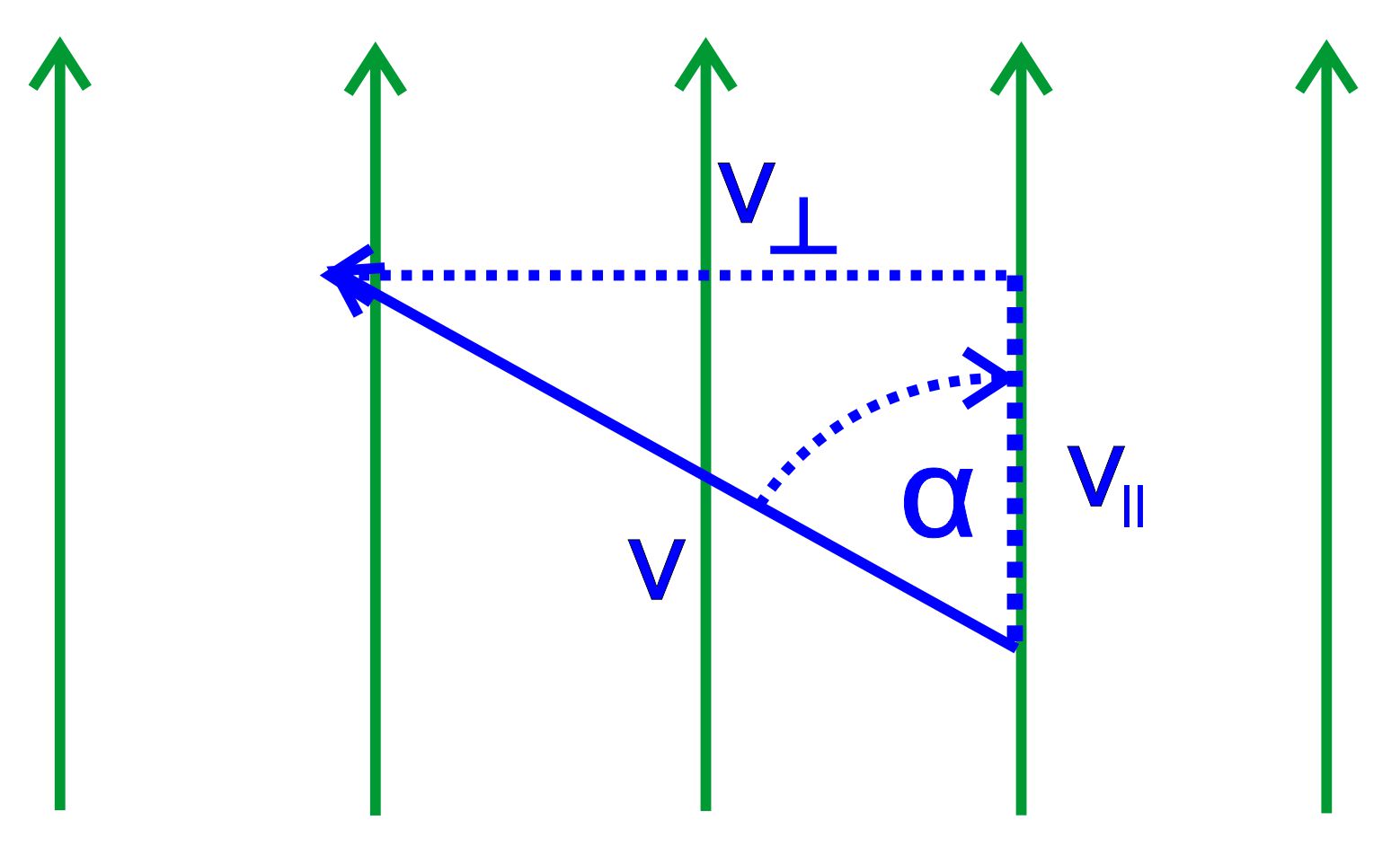
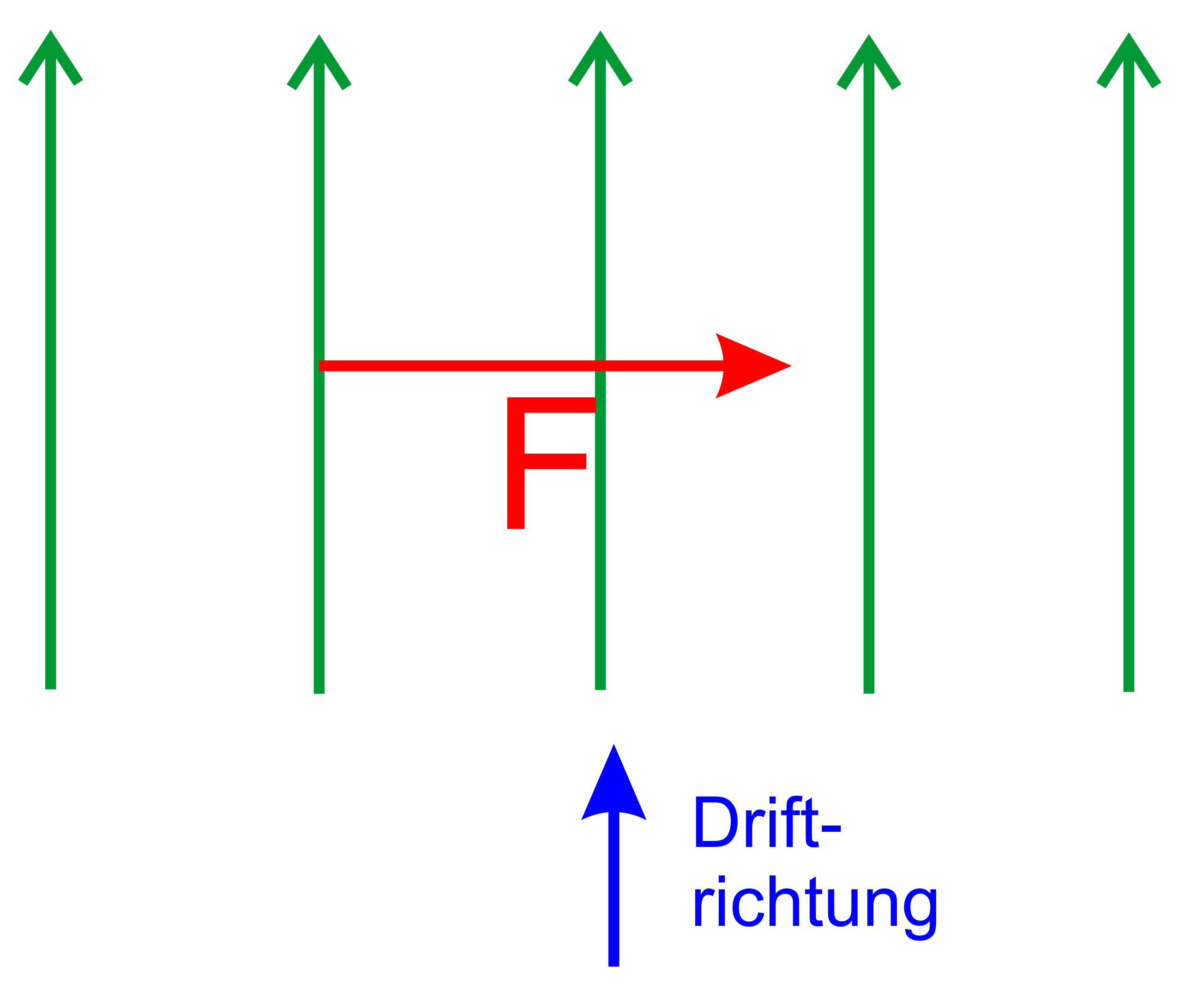
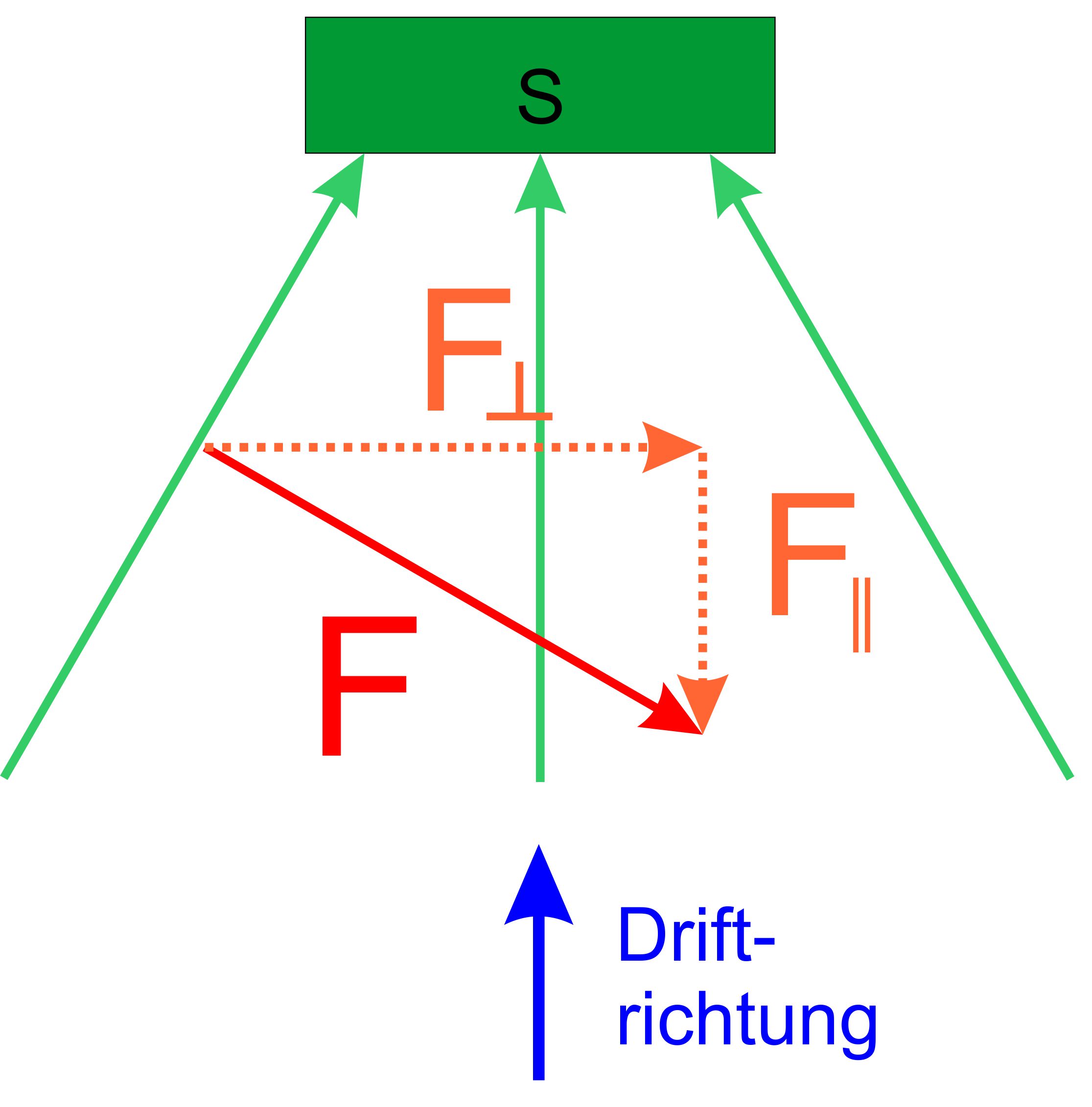
Für die
Komponenten gilt: vꞱ
= v ∙ sin(α)
und v║ = v ∙ cos(α) Nur auf
die Komponente vꞱ
wirkt die Lorentzkraft. Diese
Komponente sorgt
für eine Kreisbahn. Gleichzeitig wird das Elektron mit v║ entlang der
Feldlinien bewegt, d.h. die Kreisbahn wird entlang der Feldlinien auseinandergezogen.
Man könnte von einer „Driftbewegung“ der Kreisbahn
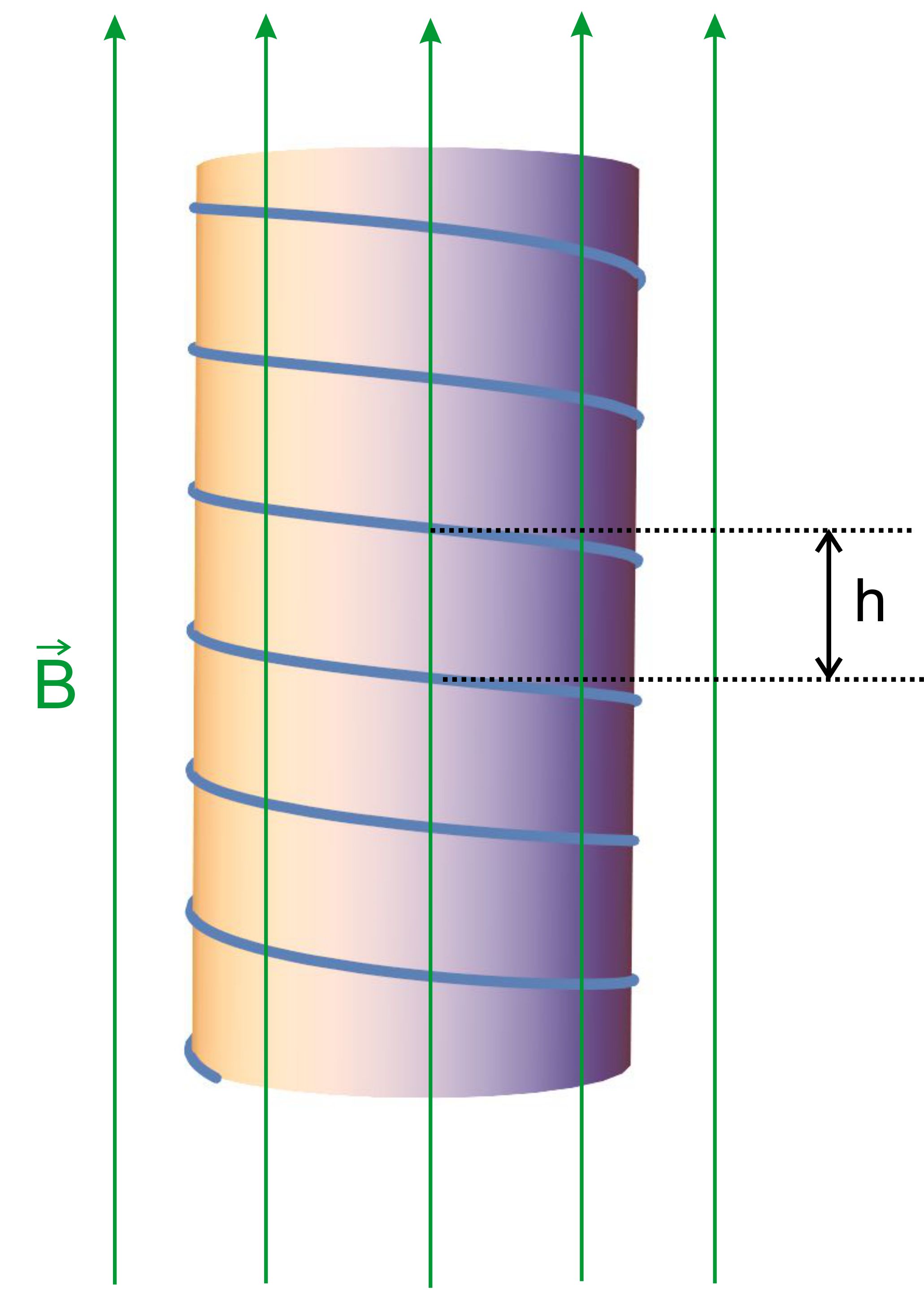
sprechen. Insgesamt erhält man eine Schraubenbahn. Wenn das
Magnetfeld homogen ist, verläuft die Schraubenbahn auf einem
„gedachten“ Zylinder, d.h. der Radius bleibt gleich groß. Die Situation ist dann in etwa wie folgt:
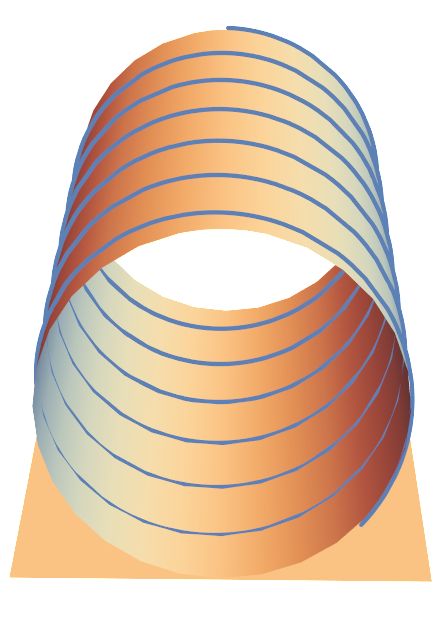
Blick von oben auf den „Zylinder“
mit der realen Schraubenbahn der Elektronen Wenn die
Elektronen in der Papierebene in das Magnetfeld schräg ein- geschossen
werden, bildet sich die Schraubenbahn oberhalb der Papierebene
aus, d.h. der Zylinder liegt auf der Papierebene auf. Also so
Hier
sieht man echte Schraubenbahn in einem Fadenstrahlrohr:
Quelle: https://virtuelle-experimente.de/b-feld/anwendung/schraubenbahn.php Es
gelten nun die folgenden Formeln:
Magnetische
Flasche − magnetischer Spiegel Im
obigen Fall gehen wir von einem homogenen Feld aus, wie z.B. im
Inneren einer Helmholtz-Spule. Es bildet sich eine Schraubenbahn mit
festem Radius aus. Der Radius der Schraubenbahn hängt von B ab, d.h.
je größer B ist, um so kleiner wird der Radius, um so „enger“ wird die
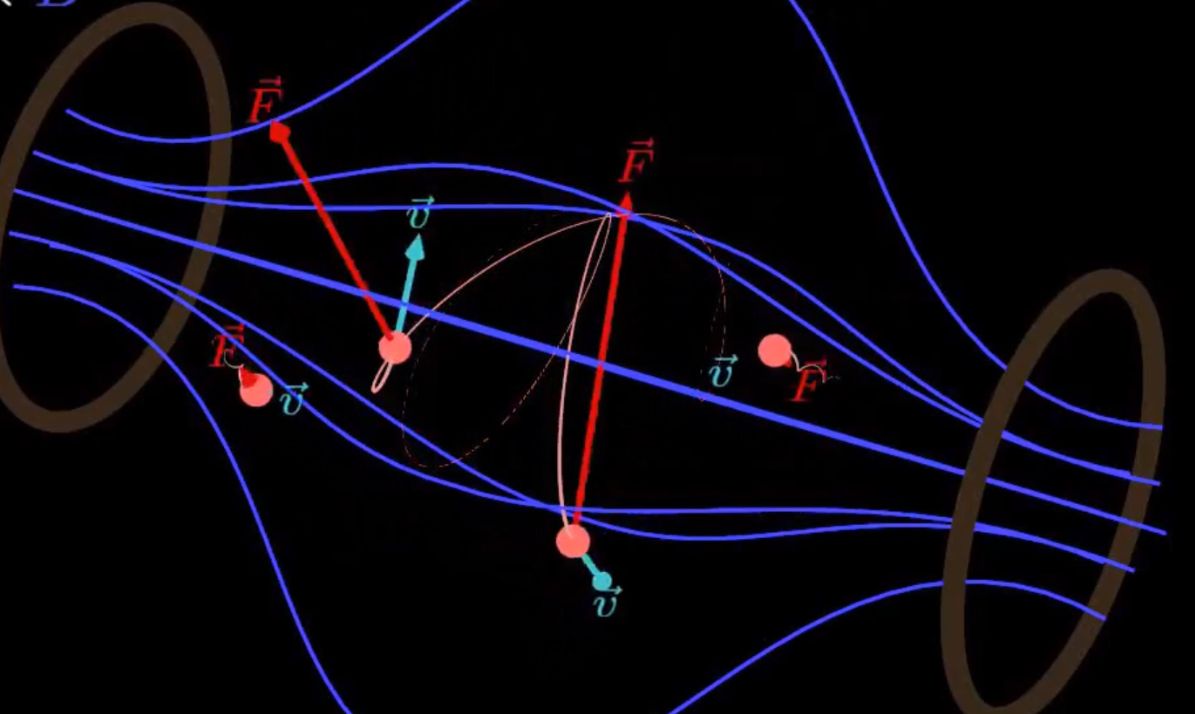
Schraubenbahn (s. Formel * ) Liegt
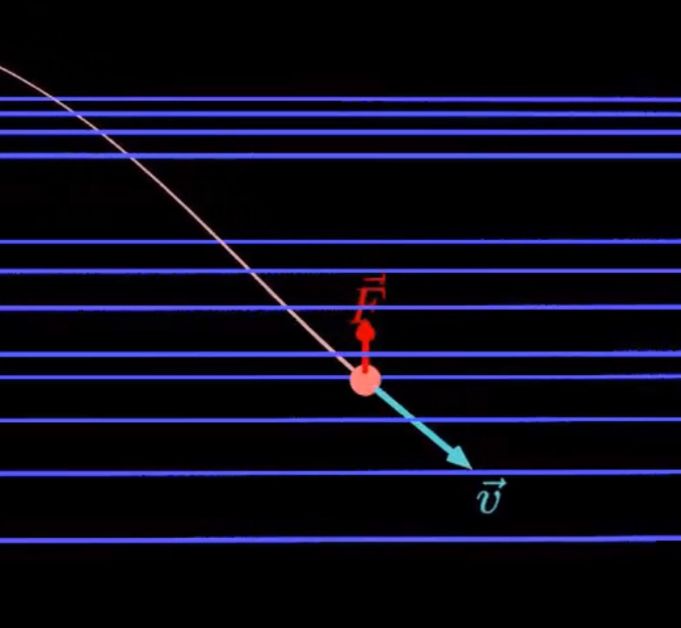
ein inhomogenes Feld vor, z. Bsp. in der Nähe eines Magnetpols wird die
Bahn deutlich komplizierter. Da hier die Feldstärke zunimmt werden
die Kreisbahnen auf jeden Fall kleiner, der Radius nimmt ab. Gleichzeitig
weist der Lorentzkraft-Vektor z.T. entgegengesetzt zur Driftrichtung. Die
folgenden Abbildungen vergleichen einmal die Verhältnisse:
Da wir im
inhomogenen Fall eine Kraftkomponente entgegengesetzt zur
Driftgeschwindigkeit vorliegen haben, wird die Driftbewegung ab- gebremst
( F = m ∙
a ). Irgendwann wird die Driftgeschwindigkeit 0
m/s und das
Elektron wird dann aufgrund der Kraftkomponente F║ in
die andere
Richtung, also zurück, bewegt. Man spricht auch von einem magnetischen
Spiegel. Die
folgende Abbildung zeigt dies noch einmal ganz gut.
Abbildung
aus dem Video: Magnetic Confinement Concepts - YouTube Diese
Abbildung stammt aus einer Video-Animation, die im Folgenden abgespielt
werden kann. Ausschnitt aus dem
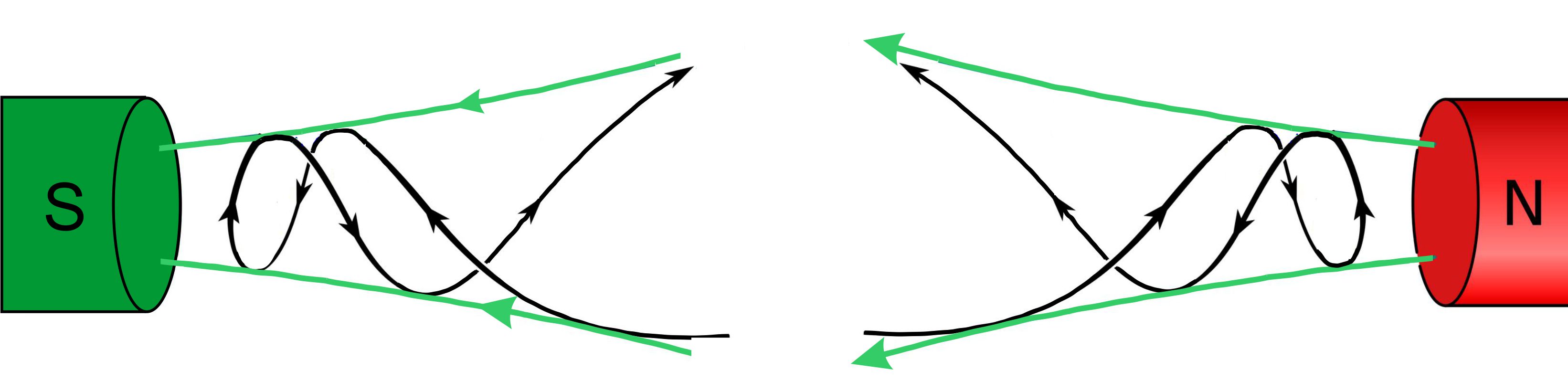
Video: Magnetic Confinement Concepts - YouTube Kombiniert
man zwei magnetische Spiegel miteinander, z.Bsp.
durch ein
Magnetfeld zwischen zwei unterschiedlichen Magnetpolen, er- hält man
eine magnetische Flasche. Aus dieser Konstellation kommen die
Elektronen nicht mehr heraus, sondern wandern immer zwischen den
Polen hin und her. Hierzu
folgende Abbildung:
Quelle:https://commons.wikimedia.org/wiki/File:Magnetic-mirror.svg Die Abbildung wurde verändert und
gespiegelt. Die Bezeichnungen von B und F entfernt, weil sie meiner Meinung nach
nur verwirren. Außerdem tritt mit dem F aus der Originalzeichnung schon eine
Beschleunigung auf, statt einer Abbremsung. In
diesem Videoausschnitt sieht man eine Animation zur magnetischen Flasche: Ausschnitt aus dem
Video: Magnetic Confinement Concepts - YouTube Die magnetische Flasche spielt für uns auf der Erde eine große Rolle, weil auch das Erdmagnetfeld grob als Dipolfeld (also Stabmagnetfeld) gesehen
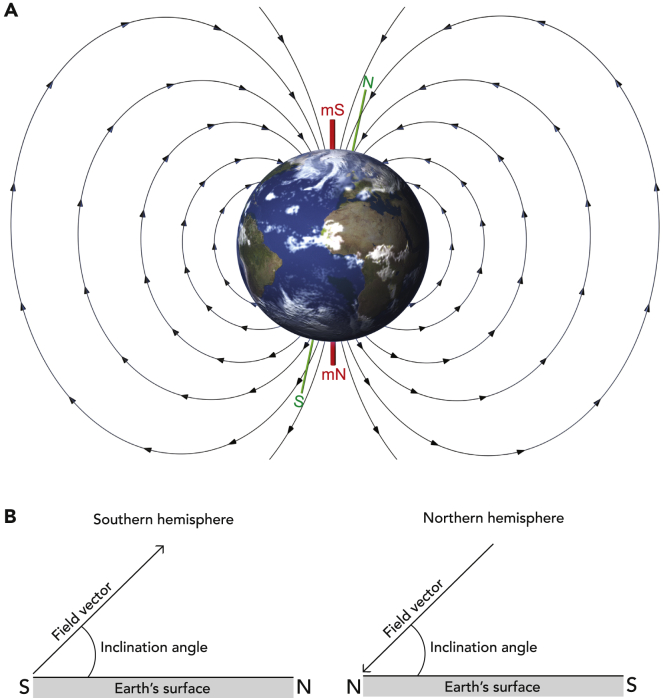
werden kann. Hierzu
folgendes Bild aus einem NASA-Artikel:
Quelle: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9167971/figure/fig1/ Man
sieht hier natürlich auch am magnetischen Nordpol und Südpol (mN,mS) extrem inhomogene Felder, so dass das Erdmagnetfeld
auch als
magnetische Flasche wirken kann. Wenn geladene Teilchen in das
Erdmagnetfeld gelangen, sind sie in diesem Feld „gefangen“ und bewegen
sich immer zwischen Nord- und Südpol hin und her. Diese geladenen Teilchen hat man auch gefunden,
diese bilden den van
Allen Gürtel.
Quelle: Van-Allen-Strahlungsgürtel – Wikipedia Der
innere Gürtel enthält bevorzugt Protonen, der äußere Gürtel Elektronen.
Über die Herkunft der geladenen Teilchen gehen die Mei- nungen noch
auseinander. Hier scheint noch Forschungsbedarf zu bestehen. Hinweis: Mehr hierzu in einem Extra-Kapitel zum
Erdmagnetfeld (in Arbeit) zum Abschnitt:
zum vorherigen Kapitel: |
|||||||||||||||||||||||||||||||||||||||||||||||||