|
gehe zu: Fall einer Leiterschleife durch ein
Magnetfeld Wir
werden bei der Klausuraufgabe
anknüpfen. In jener Aufgabe wurde
eine Leiterschleife in ein Magnetfeld hineingeschoben. Dieses Thema
war schon mathematisch anspruchsvoll. In diesem Kapitel wird es
noch komplexer, weil mehrere Kräfte angreifen und verschie- dene
Fälle betrachtet werden müssen. Man muss sich die Klausur- aufgabe
vorher angesehen haben, weil Formeln von dort in diesem Kapitel
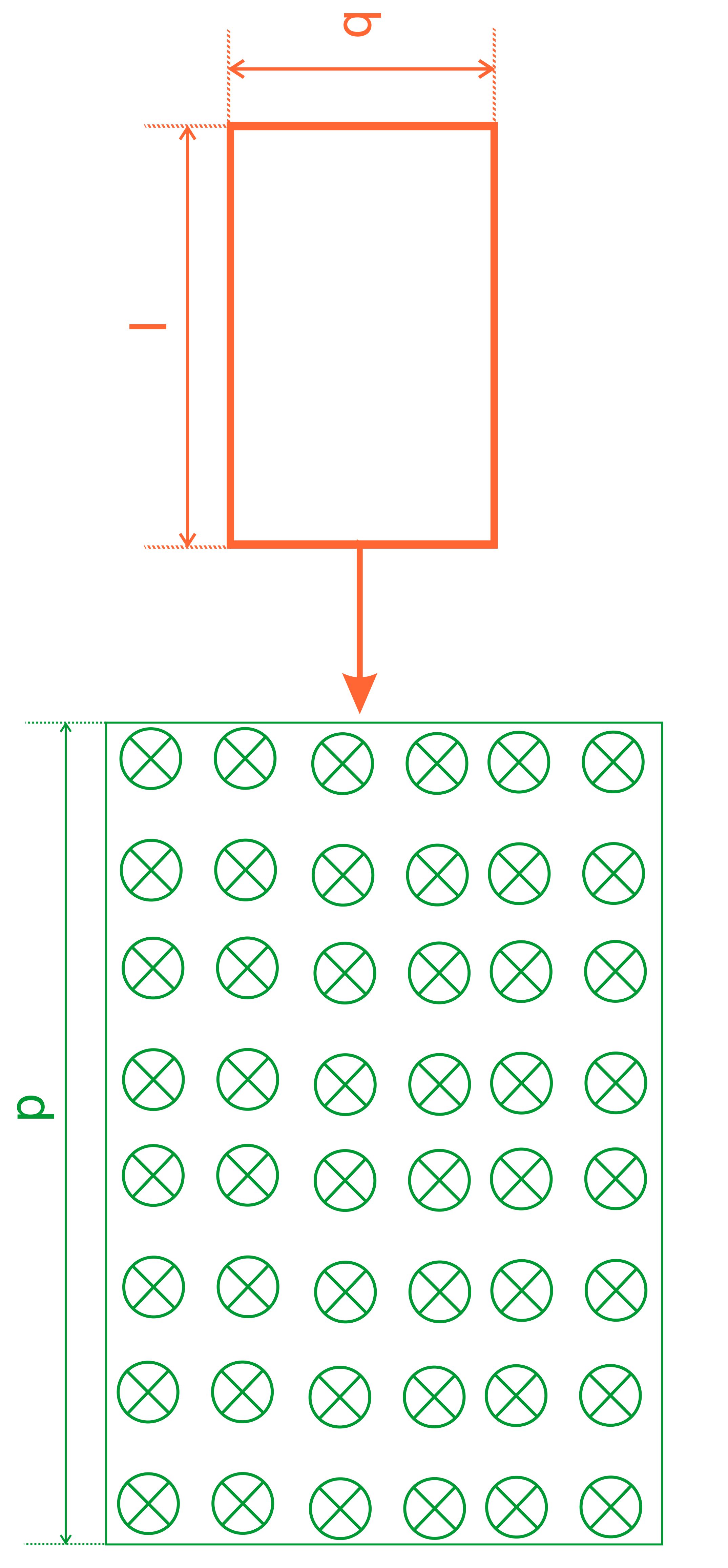
Verwendung finden. Die Situation sieht jetzt folgendermaßen aus:
Hinweis in eigener Sache: Ich habe im Internet oder in der
Literatur keinen vergleichbaren Fall gefunden, so dass ich auf meine eigenen Überlegungen angewiesen bin.
Deshalb kann ich keine Garantie für die Richtigkeit der Überlegungen geben. 1. Fall:
Leiterschleife befindet sich noch außerhalb des Magnetfeldes Es
gelten die Überlegungen zum „Freien
Fall“. Es wirkt
die Gewichtskraft FG = m ∙ g.
Die Bewegungsgleichungen lauten: s = ½ ∙ g ∙ t2 und v = g ∙ t, wenn beim Start v = 0 m/s ist. 2. Fall:
Leiterschleife taucht in das Magnetfeld ein Es
treten jetzt zwei Kräfte auf, die gegeneinander wirken, einmal die Gewichtskraft
nach unten und dann die Lorentzkraft nach oben.
Um die
Bewegungsgleichung zu erhalten, kann man die Grundgleichung der
Mechanik benutzen. Die Bestimmung der Lorentzkraft mit FL
= − k ∙ m ∙ v(t) kann man der Klausuraufgabe entnehmen. Es gilt
also:
Wir
erhalten ein interessantes Ergebnis:
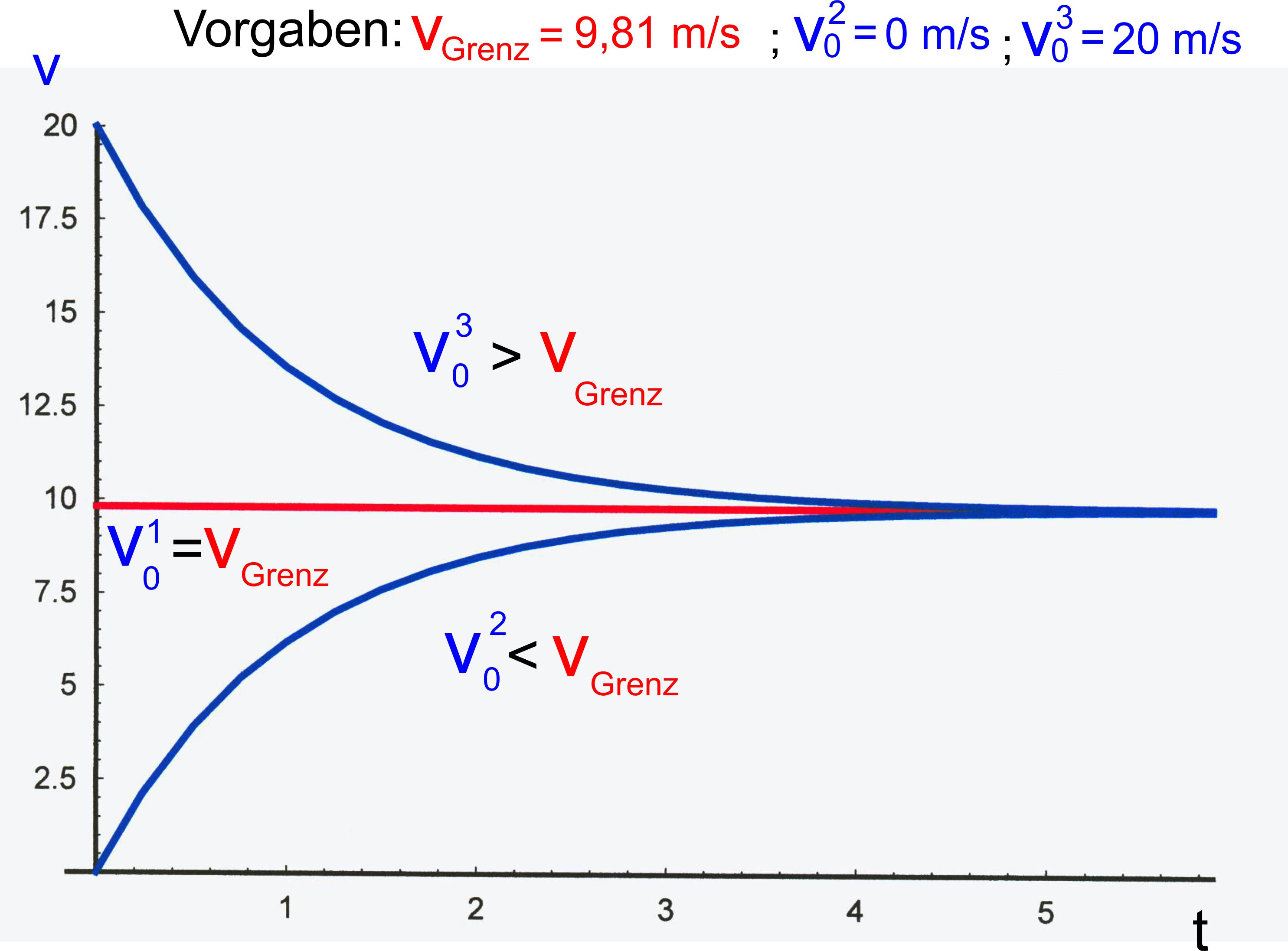
Zusammenfassung – Geschwindigkeit
Fallunterscheidung (Ein- und Austritt) Man kann
also beim Eintritt in das Magnetfeld drei
Fälle unterscheiden. 2.1. Die
Leiterschleife tritt mit der Grenzgeschwindigkeit in das Magnetfeld ein
2.2. Die
Leiterschleife tritt mit einer Geschwindigkeit v0 in das Magnetfeld ein,
die kleiner als die Grenzgeschwindigkeit ist.
2.3. Die
Leiterschleife tritt mit einer Geschwindigkeit v0 in das Magnetfeld ein,
die größer als die Grenzgeschwindigkeit ist.
Die folgenden Graphen
zeigen einmal die drei möglichen Fälle beim Eintritt
in das Magnetfeld (k = 1 gewählt):
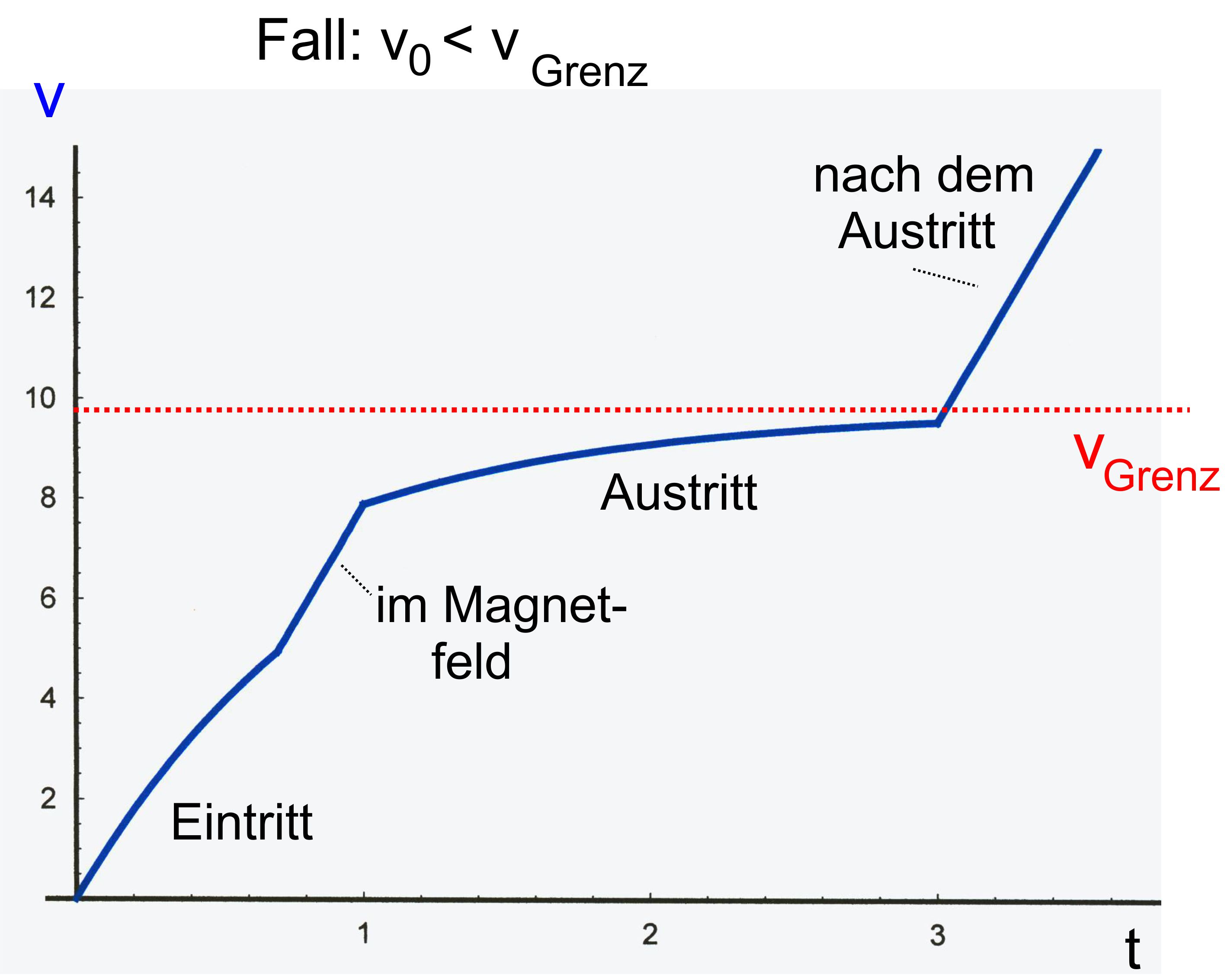
Gesamtverlauf der Geschwindigkeit beim Fall Wenn wir
den gesamten Ablauf (Eintritt, im Magnetfeld, Austritt, außer- halb des
Magnetfeldes) betrachten, wird es noch komplizierter. Der
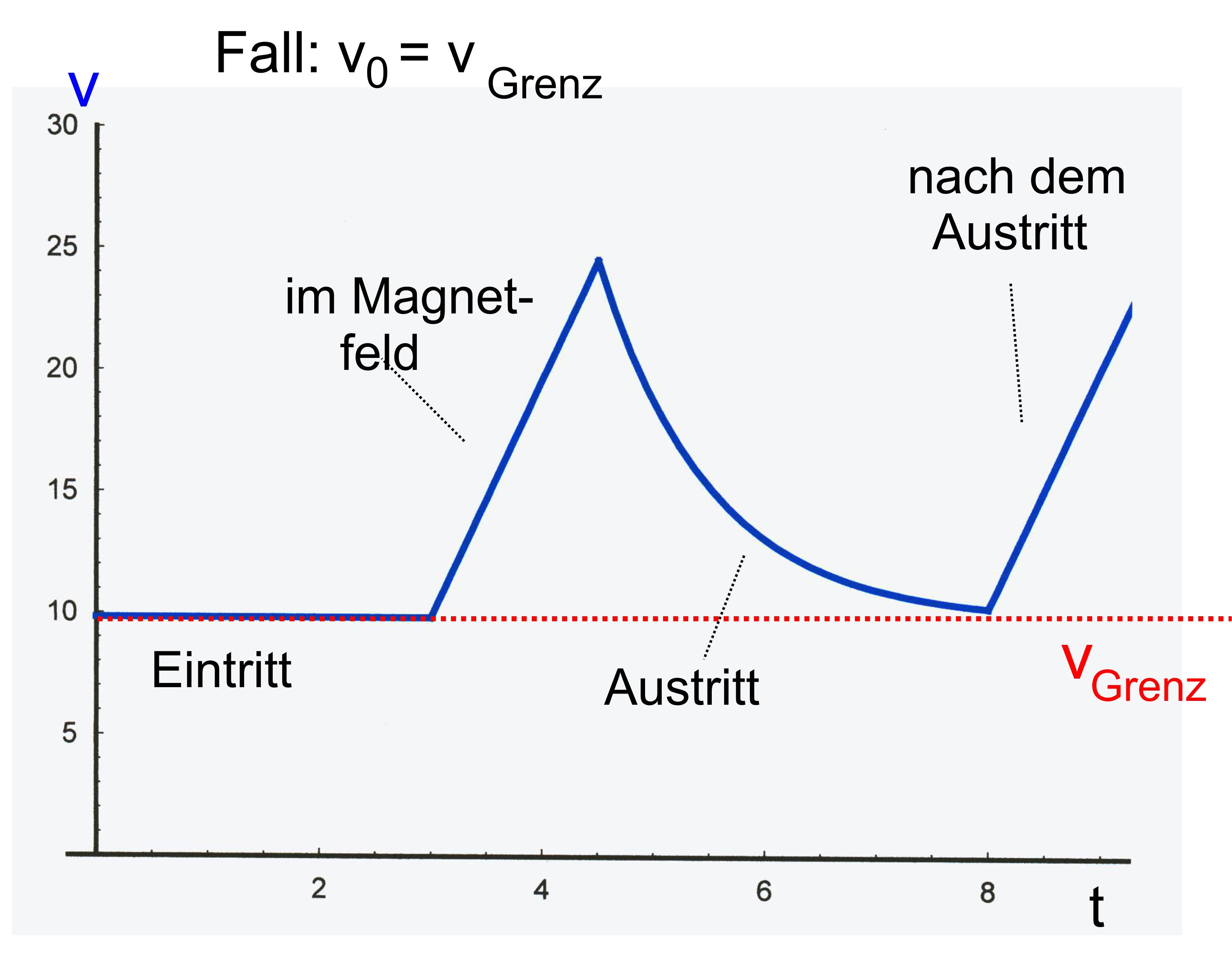
Verlauf kann sehr unterschiedlich aussehen. 1. Fall:
(s.o. 2.1.) Eintritt
mit vE = vgrenz
= g/k → konstanter Verlauf: danach
freier Fall im Magnetfeld → linearer Anstieg; Austritt
mit vA > vE
= vgrenz →
exponentieller Abfall oberhalb von vgrenz ; nach dem
Austritt wieder freier Fall → linearer Anstieg; Man hat
also folgendes Aussehen (qualitativ)(k=1)
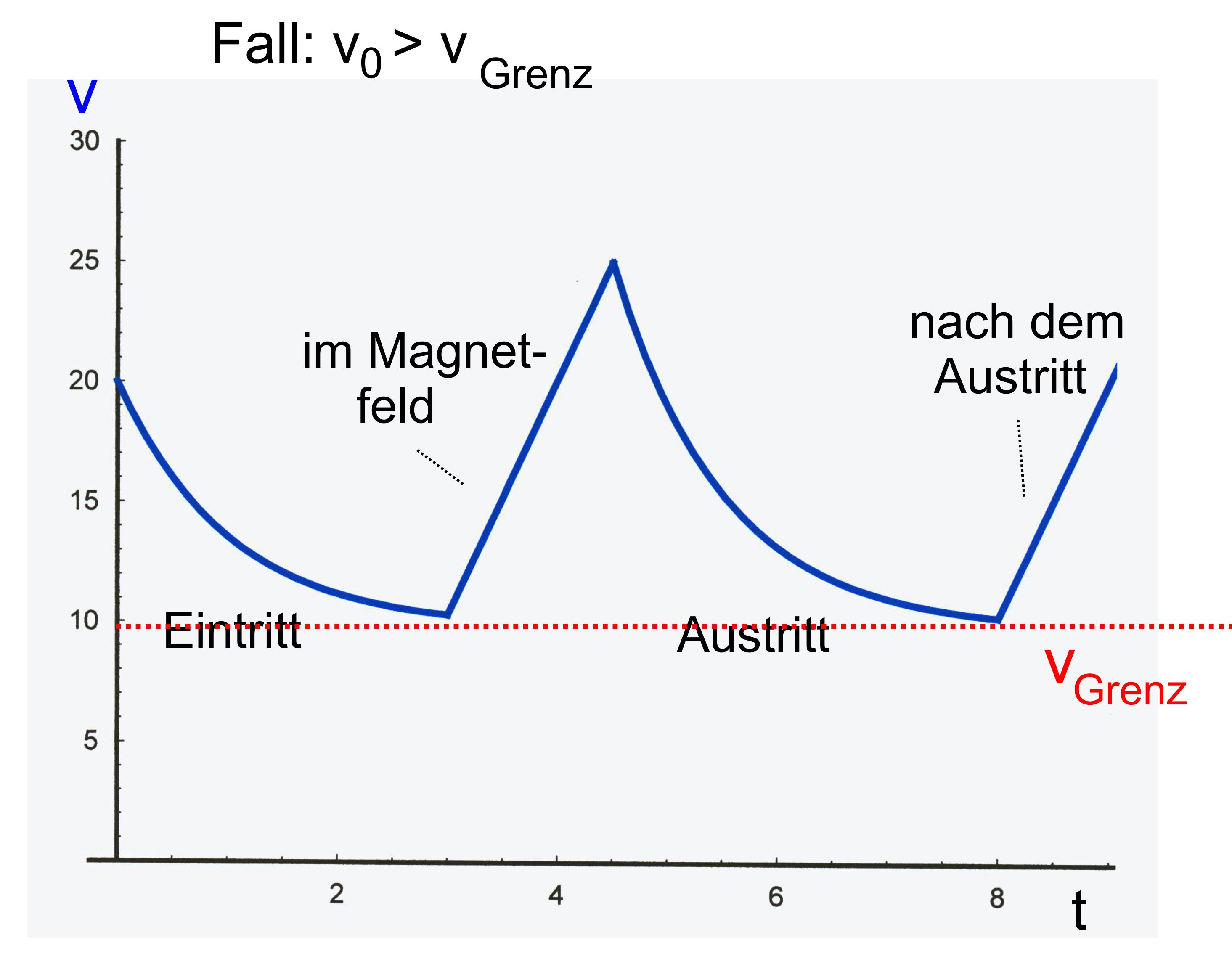
2.Fall
(s.o. 2.3): Eintritt
mit v0 > vgrenz →
exponentieller Abfall oberhalb von vgrenz ; im
Magnetfeld freier Fall → linearer Anstieg; beim
Austritt vA > vgrenz → exponentieller Abfall oberhalb
von vgrenz ; nach dem
Austritt freier Fall → linearer Anstieg Aussehen(k=1)
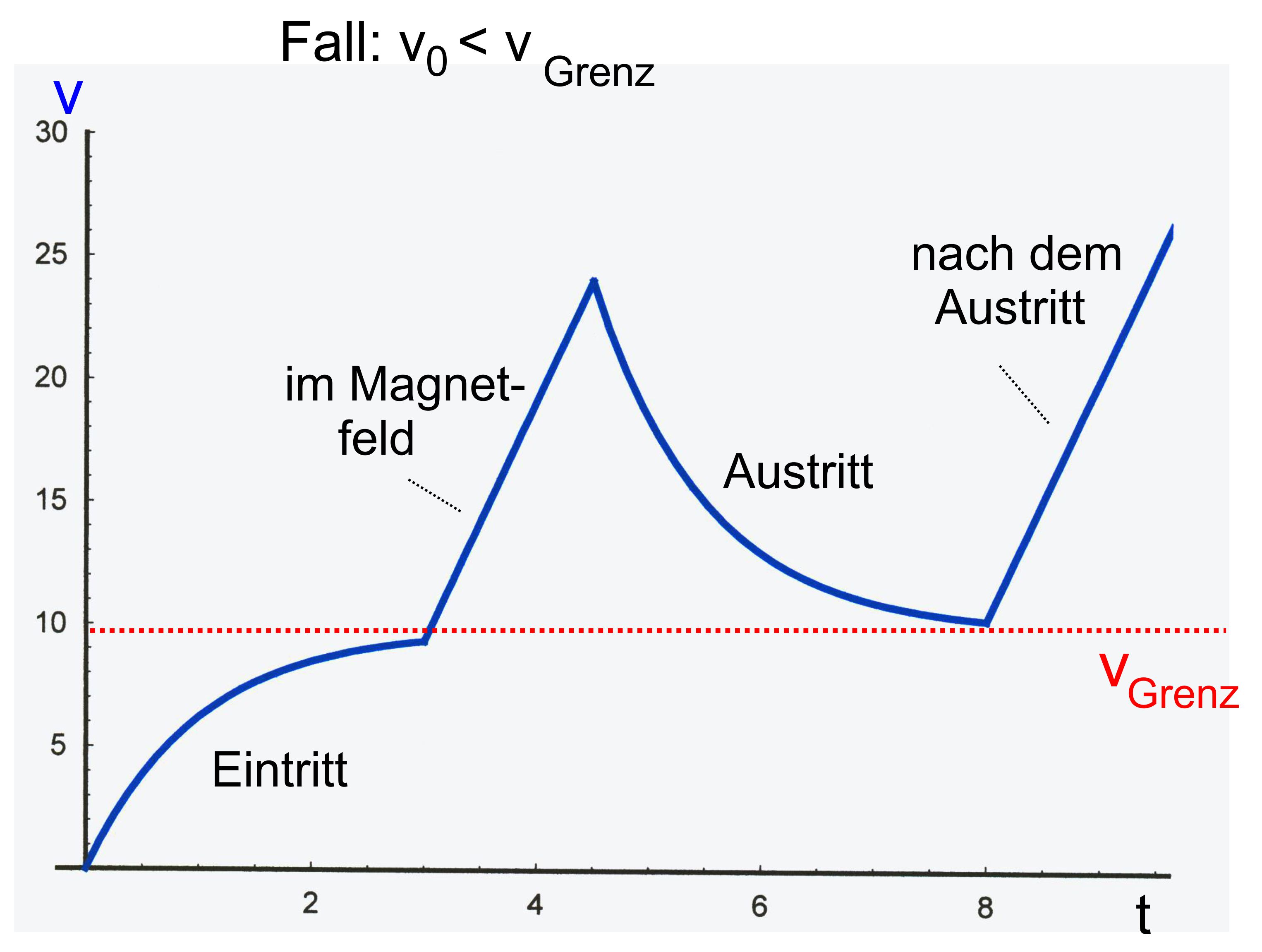
3. Fall:
(s.o. 2.2) Eintritt
mit Eintritt mit v0 < vgrenz
→ exponentieller Anstieg unterhalb von vgrenz ; im Magnetfeld freier Fall → linearer Anstieg beim Austritt
(je nach Länge des freien Falls) 3.1. vA < vgrenz
→ exponentieller Anstieg unterhalb von vgrenz ; nach dem
Austritt freier Fall → linearer Anstieg 3.2. vA > vgrenz
→ exponentieller Abfall oberhalb von vgrenz ; nach dem
Austritt freier Fall → linearer Anstieg Aussehen(k=1) 3.1.
3. 2.
Quantitative
Ergebnisse – Streckenfunktion Will man
quantitativ rechnen, braucht man auch noch die Strecken- funktion,
die angibt, welche Strecke man seit dem Zeitpunkt t = 0 s zurückgelegt
hat.
Zusammenfassung – zurückgelegte Strecke
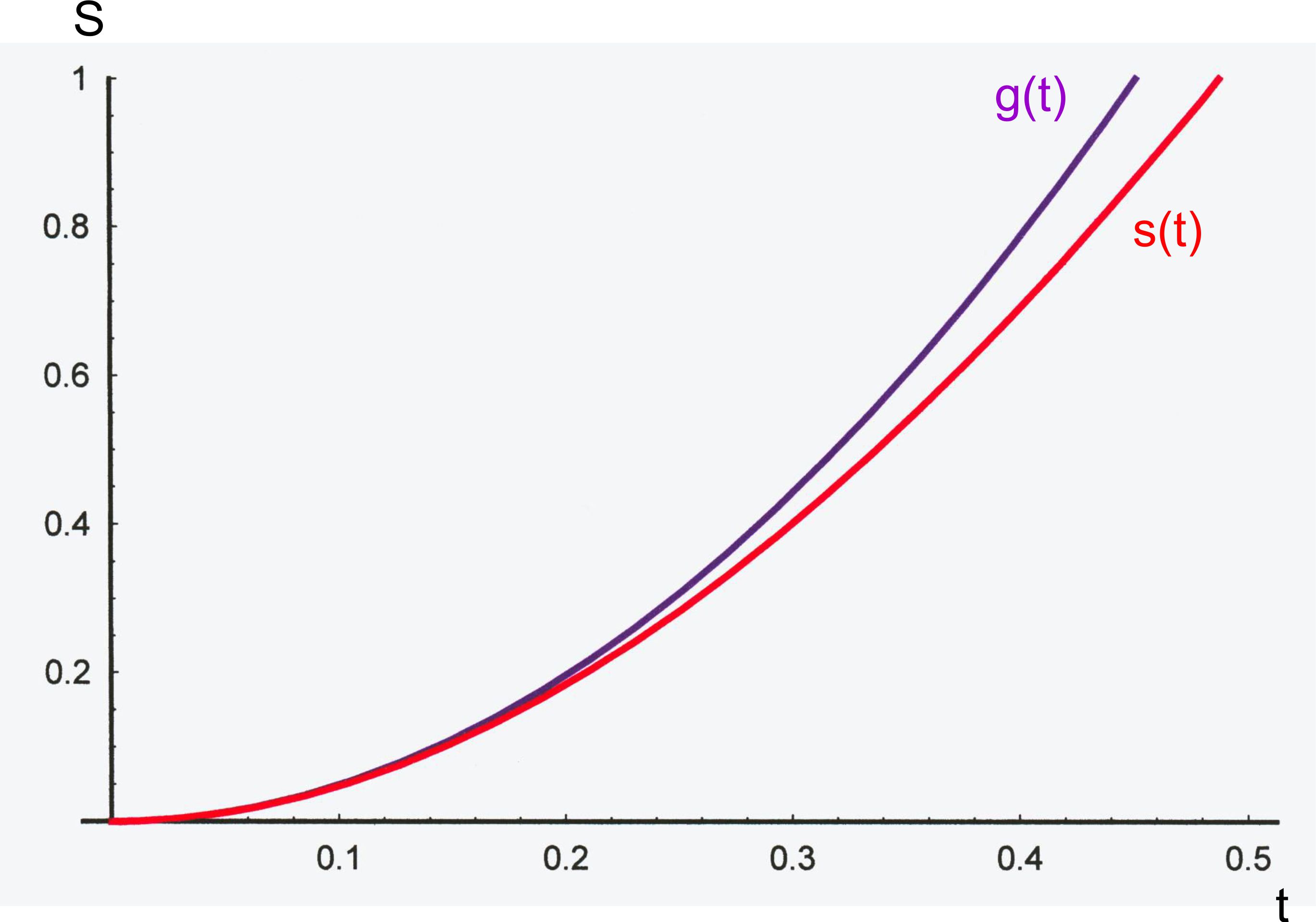
Vergleich: s(t) mit g(t) Man
kann einmal die Funktion s(t) mit der Funktion g(t) vergleichen, die
man bekommt, wenn keine Abbremsung vorliegt, also ein freier Fall.
In diesem Fall würde gelten g(t) = ½ ∙ g ∙ t2. Wir
nehmen dabei zur
Vereinfachung an, dass sich bei t = 0 s die Leiterschleife mit der Unterkante
genau an der Oberkante des Magnetfeldes befindet, d.h. v0
= 0 m/s ist. Außerdem k = 1 gewählt. Vergleich
des graphischen Verlaufes für kleine Zeiten:
Man
erkennt, dass sich die Graphen bei kleinen Zeiten, also wenn die
Abbremsung gering ist, sehr ähneln. Dies ist natürlich ein sehr vernünftiges
Ergebnis, weil dann praktisch noch ein freier Fall vor- liegt.
Erst bei größeren Zeiten und somit größeren Geschwindigkeiten steigt
die Abbremsung und macht sich in verzögerter Strecke bemerk- bar. Mathematische
Erklärung (k=1, v0 = 0 m/s): s(t) =
9,81 ∙ t + 9,81 ∙ ( e−t
– 1 ) = 9,81 ∙ t – 9,81 + 9,81 ∙ e−t Mit der
Reihenentwicklung von e−t ≈ 1 – t + ½ t2 → s(t) =
9,81 ∙ t – 9,81 + 9,81 ∙ e−t ≈ 9,81 ∙
t – 9,81 + 9,81 ∙ ( 1 – t + ½ t2 ) ≈
9,81 ∙ t – 9,81 + 9,81 – 9,81 ∙ t + ½ ∙ 9,81 ∙ t2
≈ ½ ∙
9,81 ∙ t2 = g(t) Konkrete Rechnung
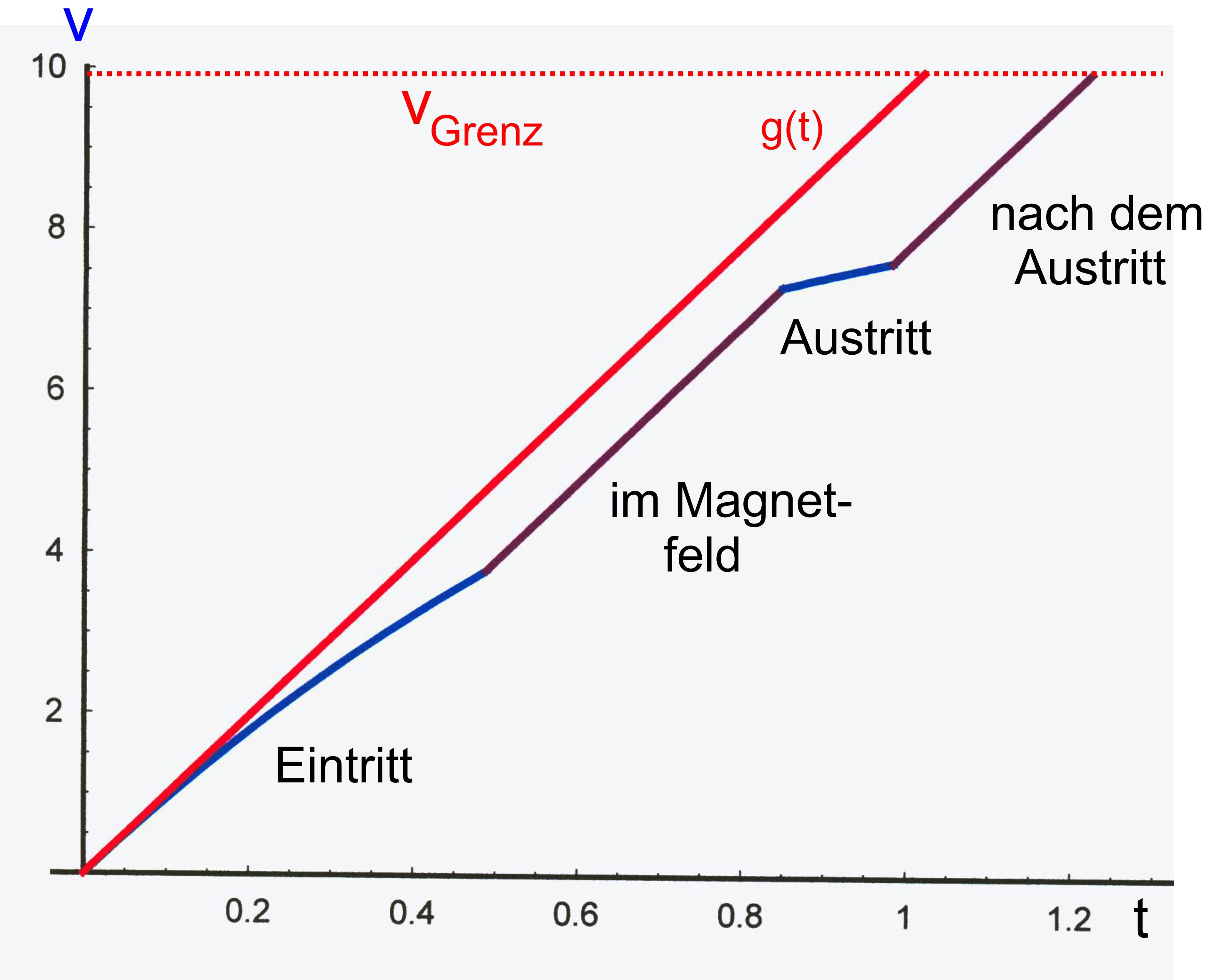
für den Geschwindigkeitsverlauf Wähle
wir, wie bisher, k = 1∙kann man recht einfache Berechnungen durchführen.
In diesem Fall wäre dann ja vgrenz =
9,81 m/s, wie oben schon
benutzt. Wir
müssen für konkrete Rechnungen jetzt noch die Länge der Leiter- schleife
und die Größe des Magnetfeldes angeben. Ich wähle l = 1 m für
die Länge der Leiterschleife und d = 3 m bzw. d = 10 m für die Größe
des Magnetfeldes. Außerdem
muss v0 noch angegeben werden bzw. die Höhe h, ab der die
Leiterschleife fallen gelassen wird. am einfachsten wählen wir h =
0 m und somit den Ausgangspunkt vom Kapitel „Vergleich s(t) mit g(t).
Es gilt dann: v0 = 0 m/s Es
ergibt sich dann:
Graph:
g(t) ist zum Vergleich mit eingetragen
Graph:
g(t) ist zum Vergleich mit eingetragen
gehe zu: zurück zu Kapitel: weiter zu Kapitel:
zurück
zur Übersicht „Induktion“ |
||||||||||||||||||||||||||||