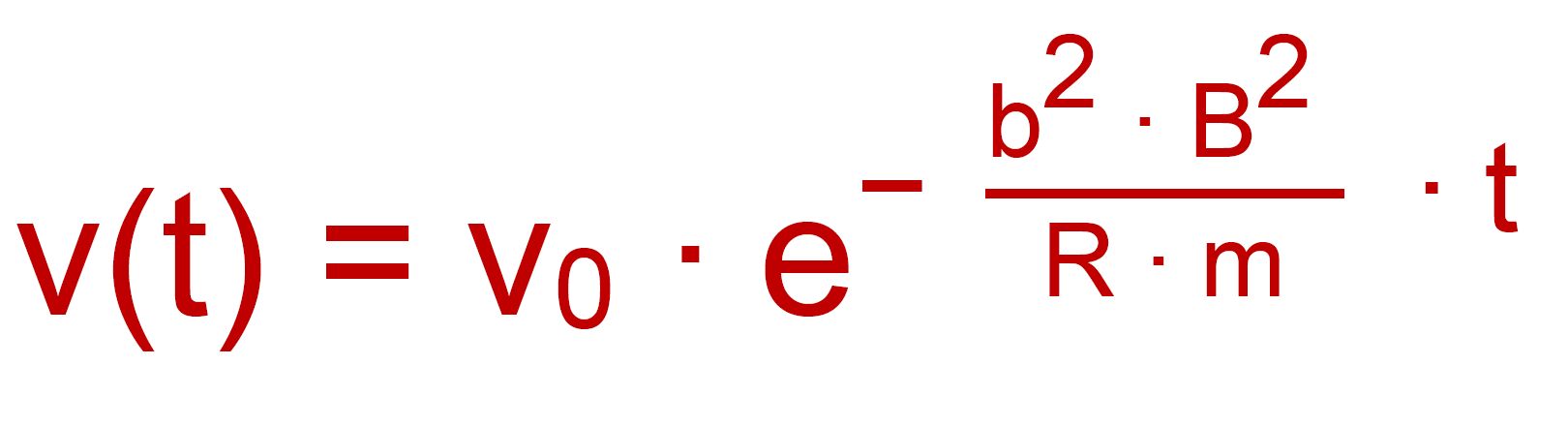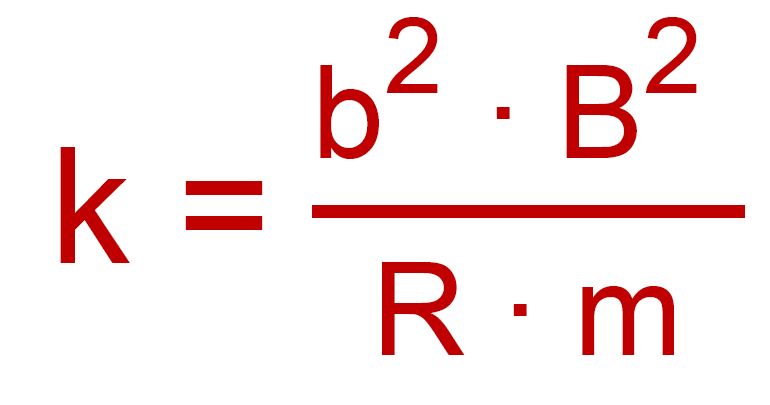Klausuraufgabe LK

Aufgabe

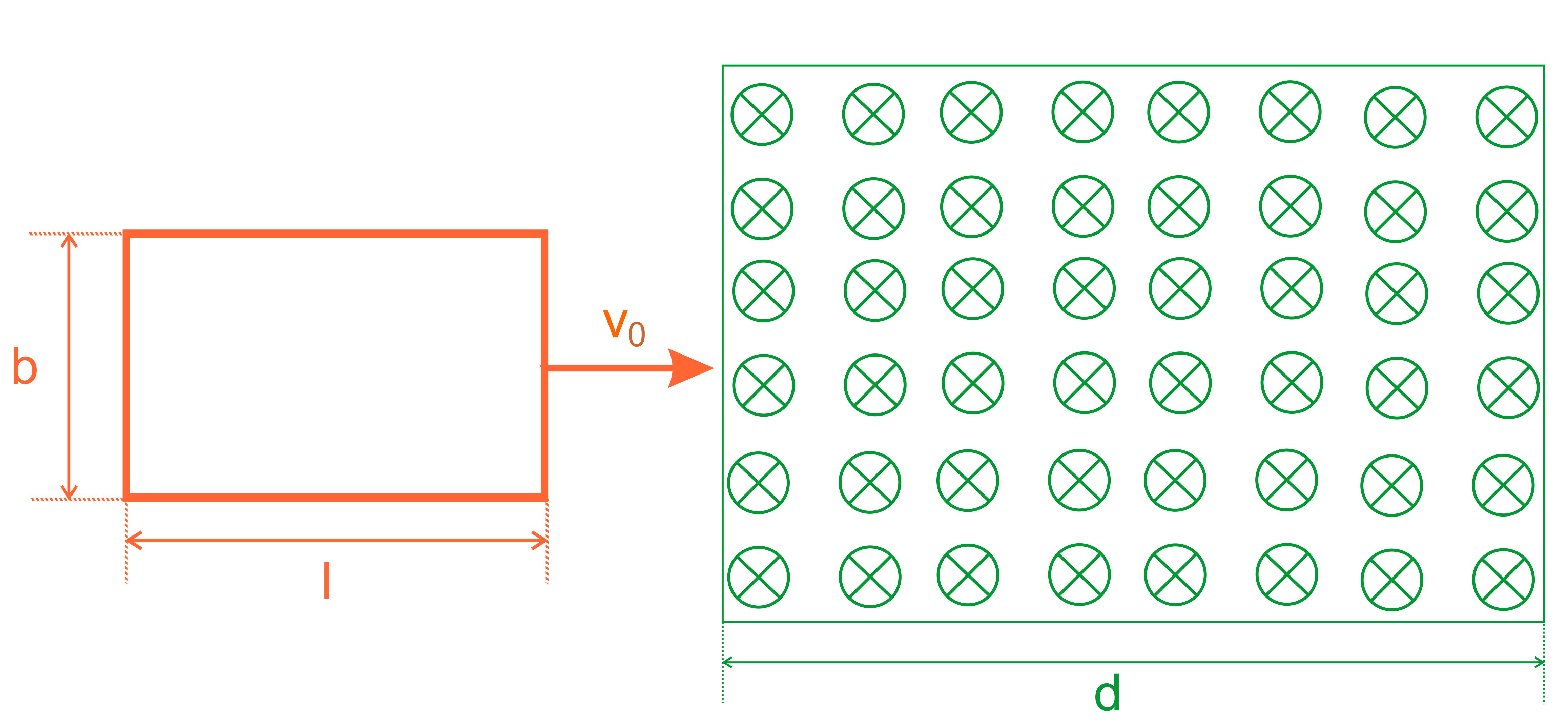
Eine rechteckige, geschlossene Leiterschleife mit dem Widerstand R

und der Länge l wird angestoßen und bewege sich reibungsfrei mit der

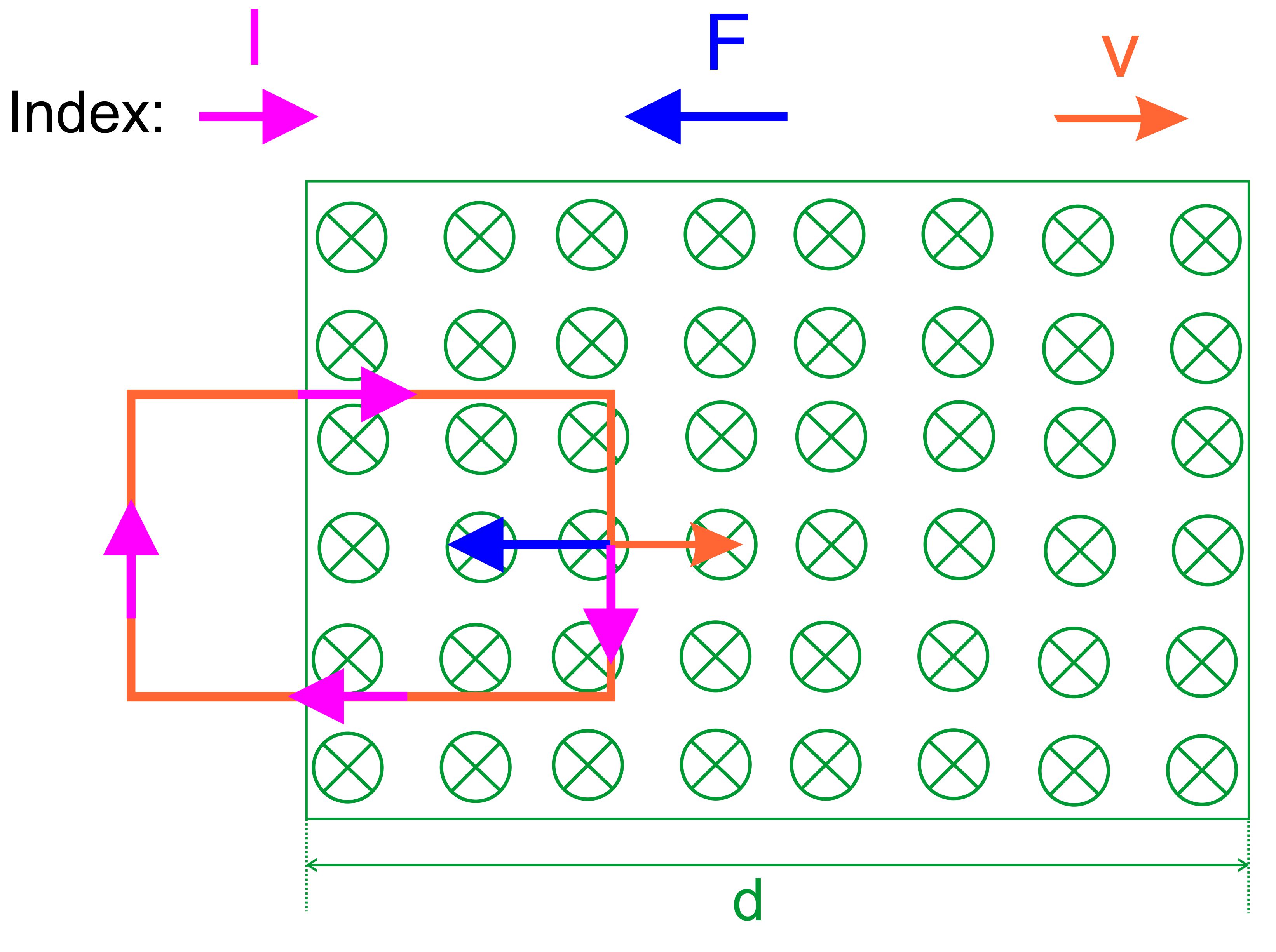
Geschwindigkeit v₀ = 1 m/s waagerecht in ein homogenes Magnetfeld

hinein (s.Abb.).

a.) Welche Kräfte treten zu Beginn des Eintritts in das Magnetfeld auf?

In welche Richtung zeigen diese Kräfte? Welchen Betrag haben diese

Kräfte, wenn die Spule b = 6 cm breit und l = 15 cm lang ist? Die

Spule sei aus Aluminiumdraht mit einem Durchmesser von d = 5 mm

gefertigt. Das Magnetfeld habe eine magnetische Feldstärke von

B = 150 mT.

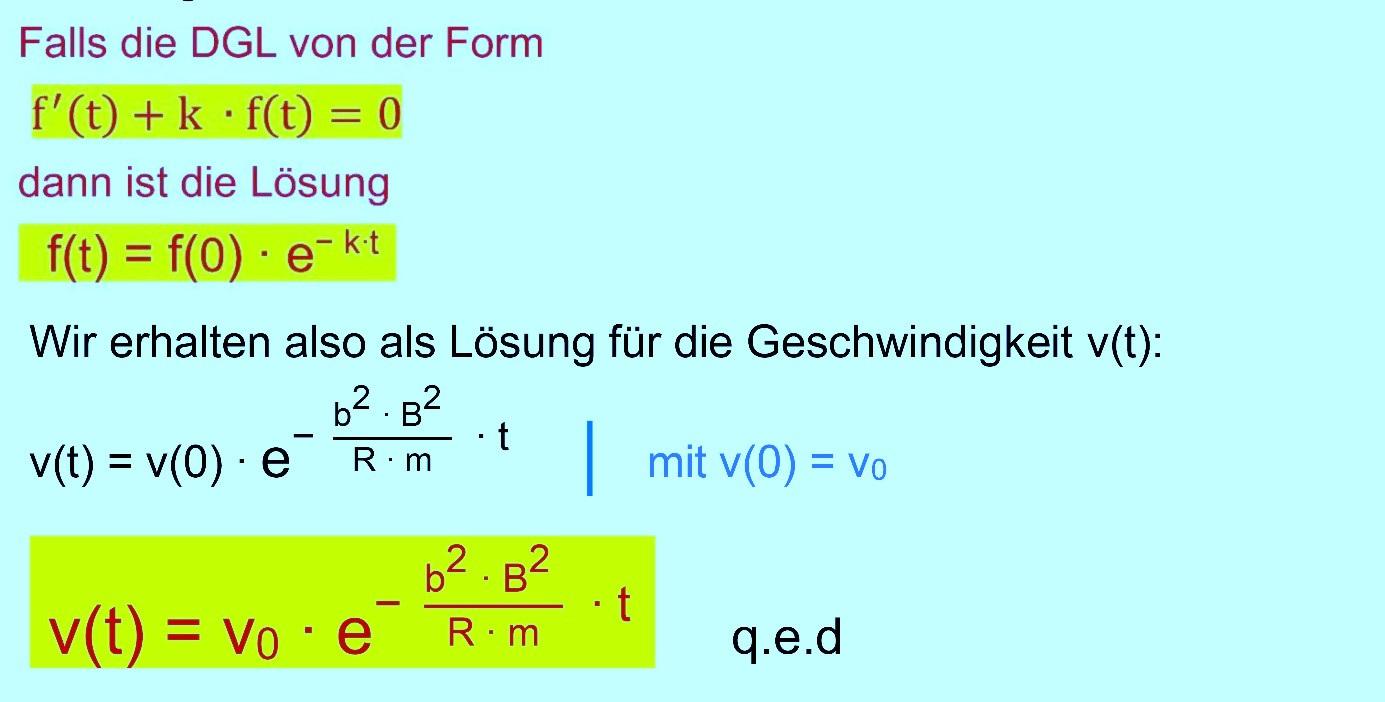
b.) Leiten Sie ausführlich her, dass der zeitliche Verlauf der Geschwin-

digkeit sich während des Eintritts mit Hilfe der Formel

bestimmen lässt. Es gilt: t = 0 s ist der Beginn des Eintritts, t endet

beim vollständigen Eintritt der Leiterschleife in das Magnetfeld.

Hinweis: Verwenden Sie zur Herleitung die Grundgleichung der Mechanik und beachten Sie, dass gilt a(t) = v'(t). Außerdem wirkt F entgegengesetzt zu v (®negatives Vorzeichen).

c.) Bestimmen Sie für den vorgegebenen Fall die Größe k mit

Berechnen Sie dann, die Geschwindigkeit, die sich nach 100 ms ergibt.

Nach welcher Zeit beträgt die Geschwindigkeit nur noch 0,6 m/s ?

Lösung:

a.)

b.)

c.)

.

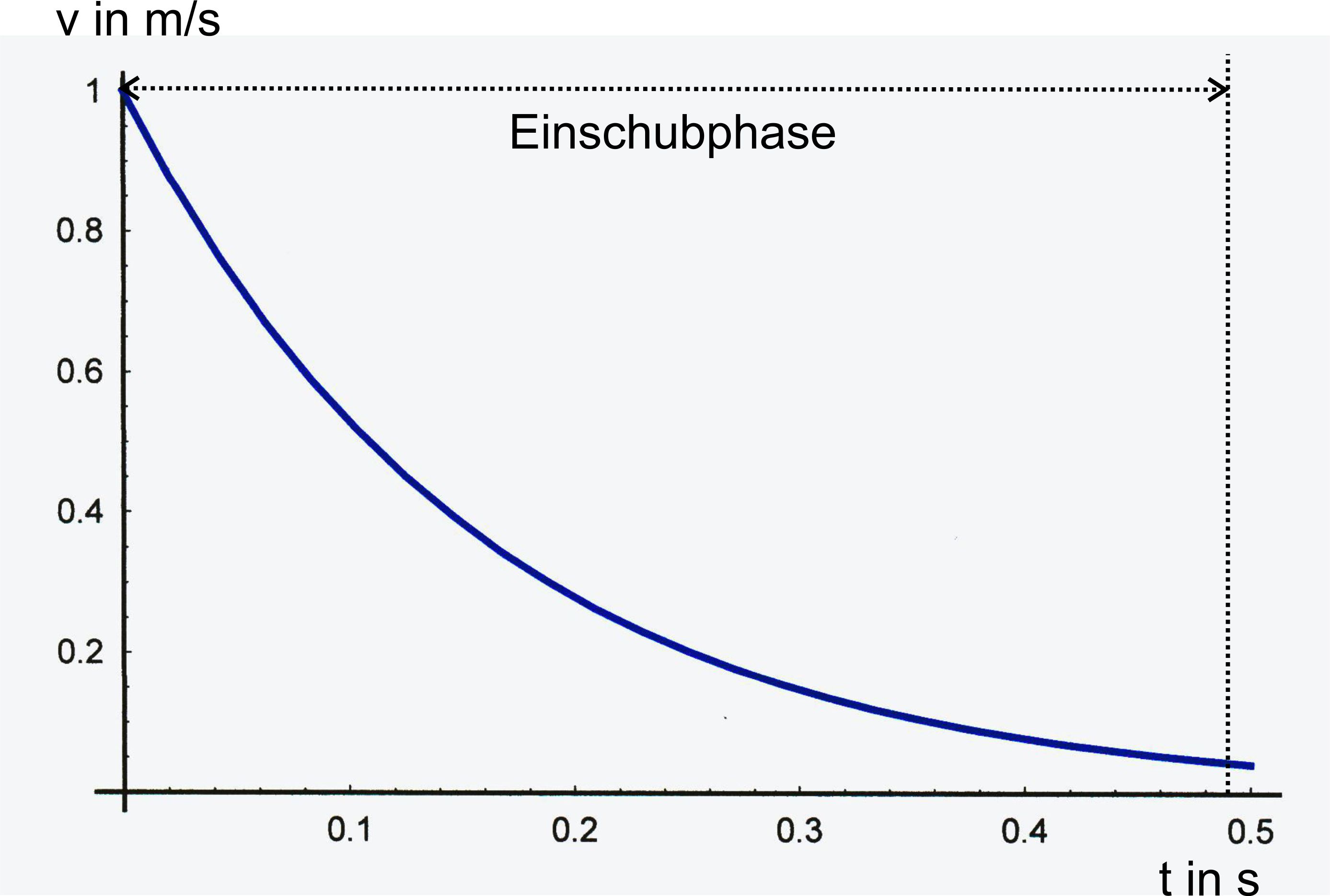
Exkurs: Graphen für v(t) und s(t)

für die Einschubphase bei obigen Vorgaben:

Hinweis: die Graphen von U_ind(t), I(t) und F(t) haben einen ähnlichen Verlauf, weil diese direkt

von v(t) abhängen.

Exkurs: was passiert nach dem Einschub?

Während des Einschubes wirkt ja eine abbremsende Lorentzkraft

auf die Leiterschleife ein. Ist die Leiterschleife vollständig eingetaucht,

entsteht keine Induktionsspannung mehr, somit gibt es auch keine

abbremsende Lorentzkraft. Die Leiterschleife bewegt sich gleichförmig

im Magnetfeld weiter. Es liegt die Geschwindigkeit vor, die sich am

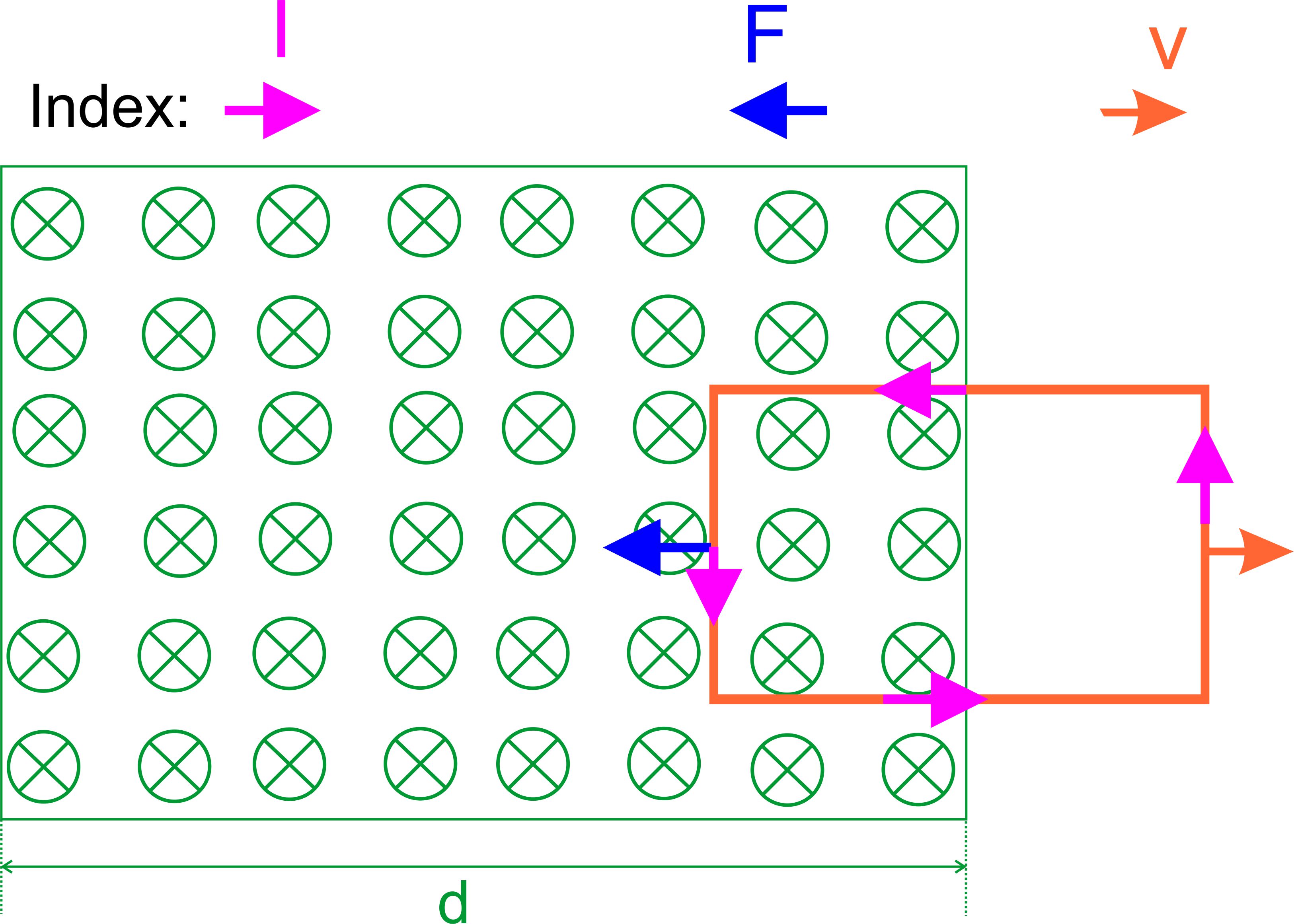
Ende des Einschubes eingestellt hat. Tritt die Leiterschleife wieder

aus dem Magnetfeld aus, liegen die Verhältnisse wie beim Einschub

vor. Wegen der Lenzschen Regel tritt eine Lorentzkraft auf, die ab-

bremsend wirkt, da der Austritt aus dem Magnetfeld behindert werden

soll. Lorentzkraft, Induktionsspannung und Stromstärke sind geringer

als beim Einschub, da hierbei die Geschwindigkeit eingeht, die aber

beim Austritt geringer ist als beim Eintritt. Der Strom fließt entgegen-

gesetzt zur Richtung beim Eintritt. Die Geschwindigkeit sinkt beim Aus-

tritt wieder exponentiell. Die Formeln von oben bleiben erhalten. Es

wird nur die Anfangsgeschwindigkeit angepasst. Nach dem vollständi-

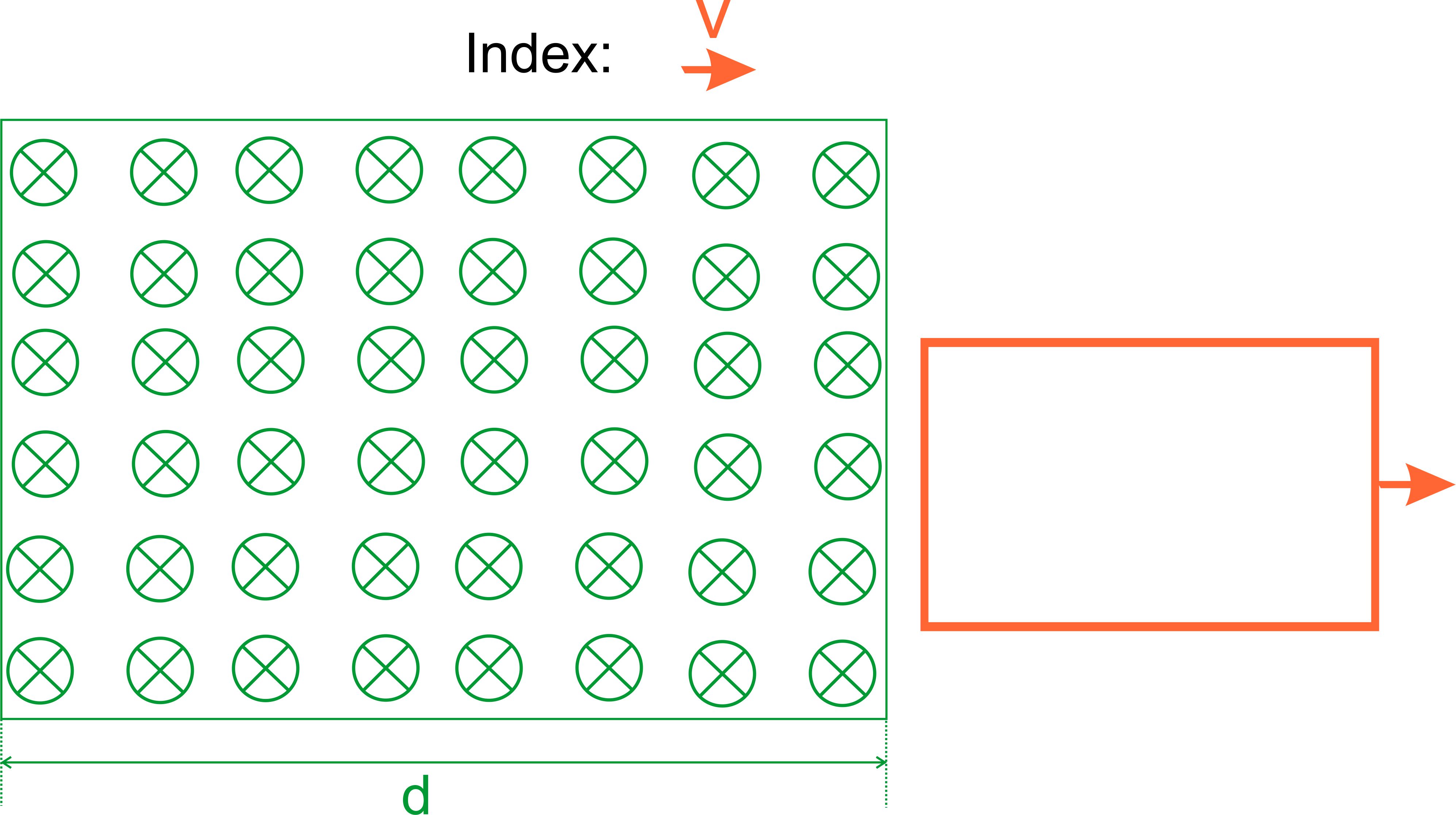
gen Austritt bewegt sich die Leiterschleife gleichförmig weiter mit der

Austrittgeschwindigkeit.

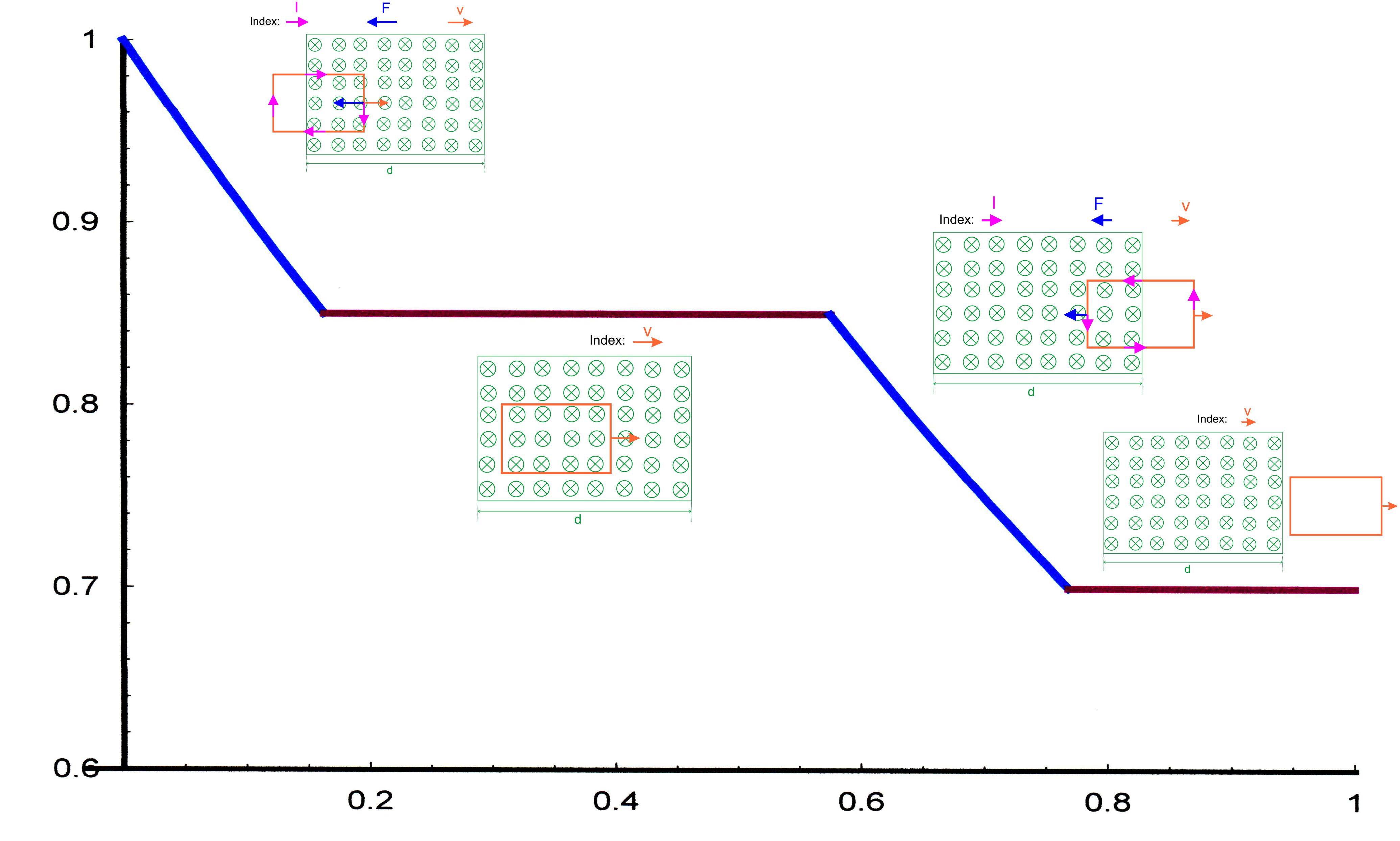
In den folgenden Abbildungen sieht man noch einmal die Verhältnisse.

(s. hierzu Kapitel: 1.1.2. Induktion)

Nach der Drei-Finger-Regel entsteht eine Lorentzkraft, die die Elektronen im rechten Teil nach unten bewegt. Es tritt ein Strom auf. Dieser Strom hat eine Lorentzkraft zur Folge, die abbremsend auf die Leiter- schleife wirkt. Die Geschwindigkeit nimmt dadurch exponentiell ab. Dies hat wieder Folgen für F und I.	Die Bewegung führt auf der rechten und linken Seite zu der gleichen Verschiebung der Elektronen, so dass kein Stromfluss auftritt. Damit gibt es keine Lorentzkräfte und so- mit keine abbremsenden Wirkung. Die Ge- schwindigkeit bleibt konstant.
Verhältnisse wie beim Eintritt. Die Lorentz- kräfte wirken jetzt allerdings auf den linken Leiterteil, so dass die Stromrichtung sich ändert.	Keine Bewegung im Magnetfeld, somit tritt keine Induktion auf.

Hierzu einmal die entsprechende Mathematik. Ich wähle in diesem Fall k = 1 und v = 1 m/s, da die Darstellung und Rechnung einfacher er-

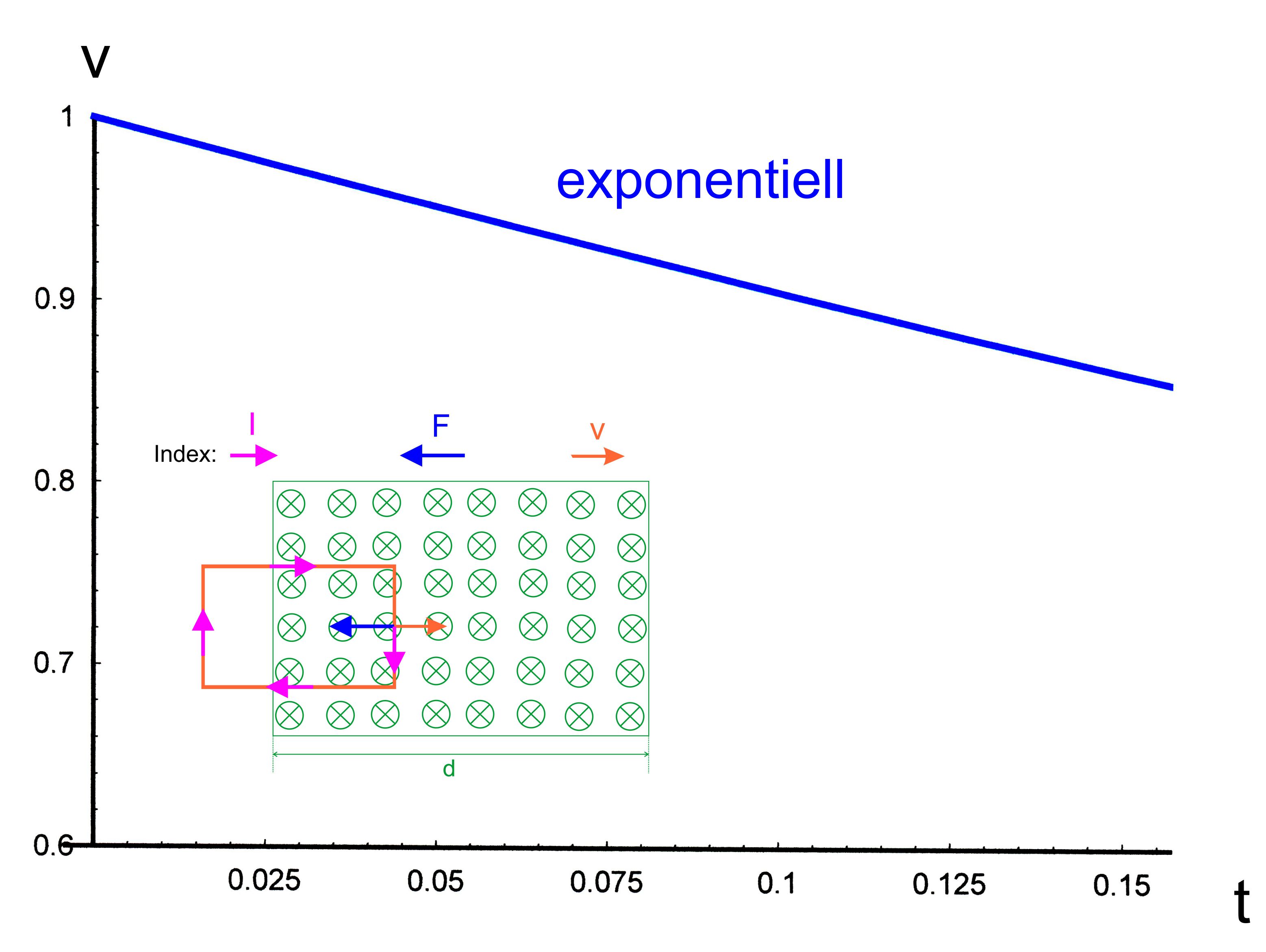
folgen kann. Weitere Annahme: B-Feld ist d = 50 cm breit

1. Fall: Einschub k = 1, v = 1 m/s, Formeln von oben

Exponentieller Abfall der Geschwindigkeit. Es gilt:

Graph dazu:

leider kann man den exponentiellen Verlauf kaum erkennen. Dies liegt daran, dass wir bei zu kleinen Argumenten bleiben, dann gilt:

e^−t ≈ 1 – t (Reihenentwicklung)

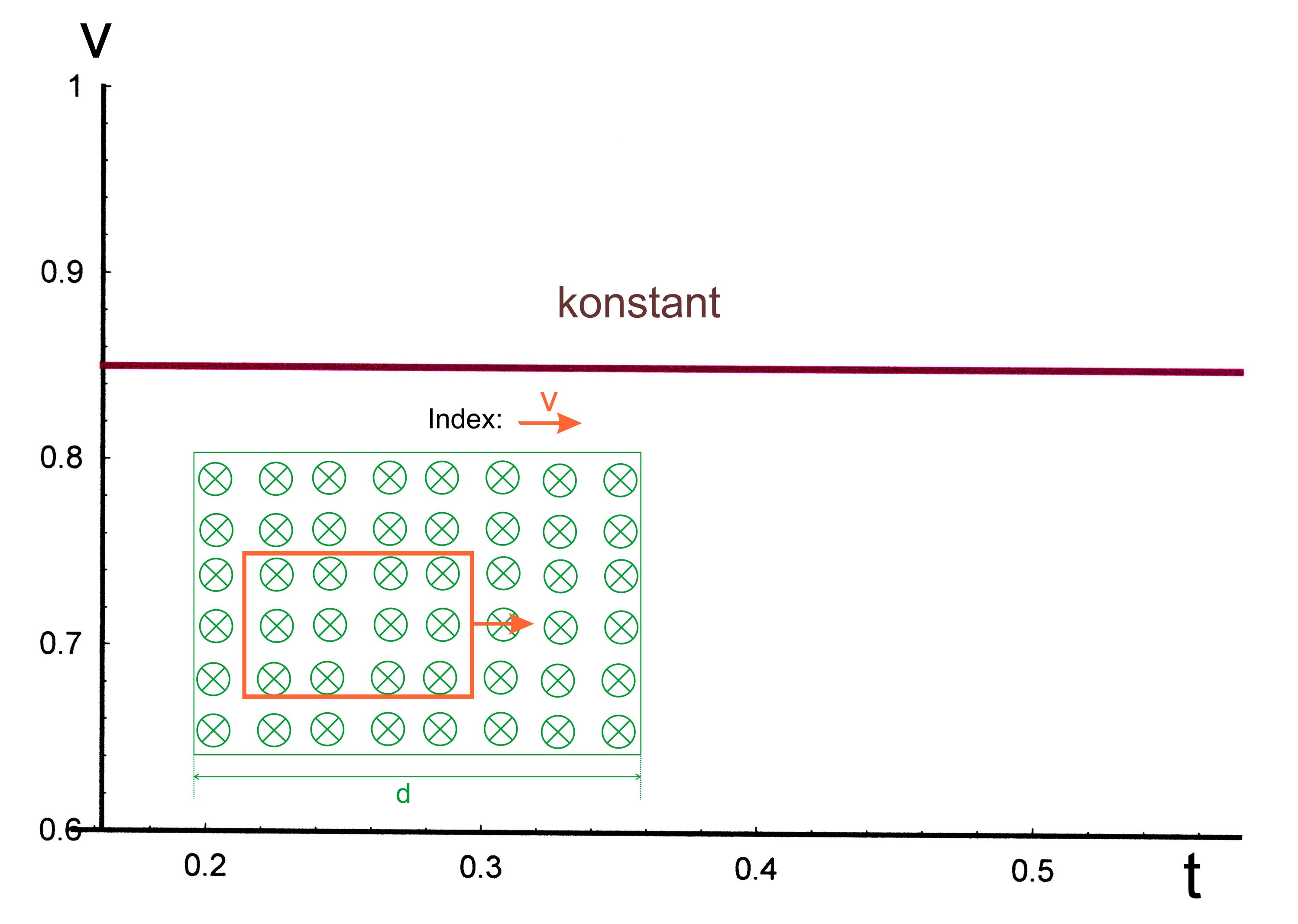
2.Fall: Leiterschleife vollständig im Magnetfeld

v bleibt konstant, v₁ (nach vollständigem Einschub) wird über die Einschubzeit

t₁ bestimmt, die man erhält, indem man über die Strecke s = 0,15 m

diese Zeit gewinnt.

Graph dazu:

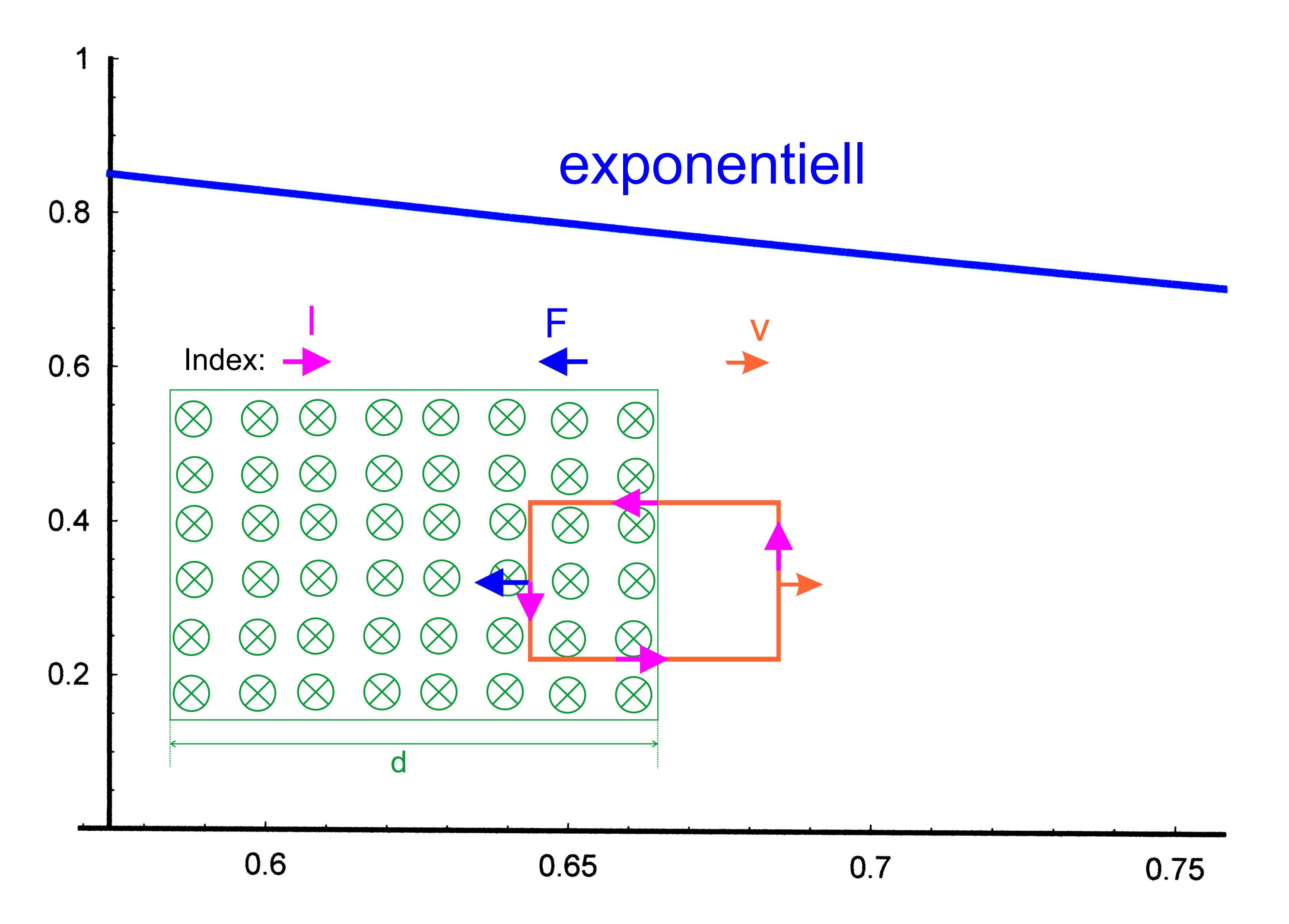
3. Fall: Austritt aus dem Magnetfeld

Die vom Magnetfeld durchsetzte Fläche ändert sich. Es gilt das

Induktionsgesetzt 1. Teil. Lenzsche Regel tritt auf usw.

Graph dazu:

(s. zweiter Fall)

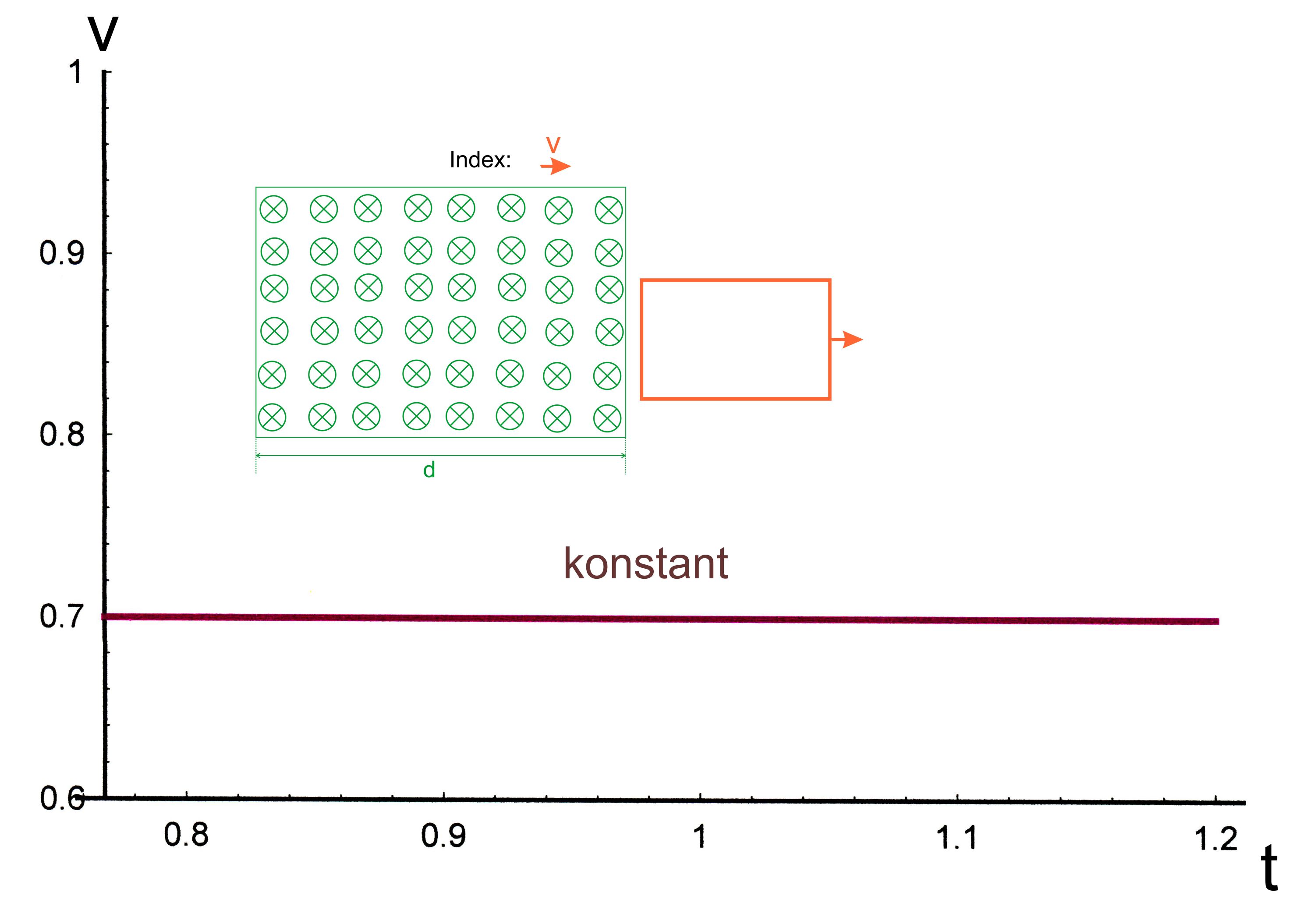
4. Fall: Leiterschleife außerhalb des Magnetfeldes

v = konstant, gleichförmige Bewegung (keine Reibung)

Graph dazu:

Zusammenfassung:

zurück zum Kapitel: Lenzsche Regel

zurück zur Übersicht „Induktion“