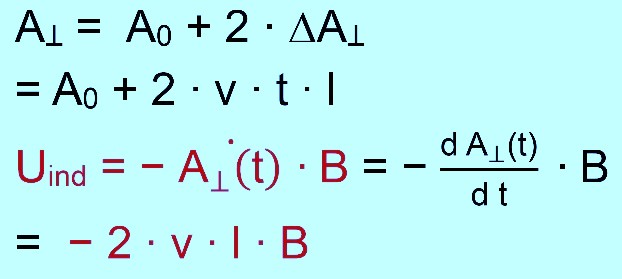|
gehe zu: Induktionsgesetz−1.Teil Änderung der Fläche durch Bewegung Wir
betrachten im folgenden Kapitel die Spannungserzeugung (Induk- tion) durch
eine nicht drehende Bewegung. Die drehende Bewegung wurde im
ersten Teil der
Betrachtung zur Induktion behandelt. Es bot sich an, die Drehung einer
Leiterschleife im Magnetfeld als erstes zu betrachten, weil sie an den
Gleichstrommotor anschließt. Jetzt
sollen einfache geradlinig gleichförmige Bewegungen im Mag-netfeld betrachtet werden. Es werden drei Fälle
unterschieden: 1.Fall:
die Leiterschleife befindet sich die ganze Zeit vollständig im Magnetfeld 2. Fall:
die Leiterschleife wird in das Magnetfeld oder aus dem Magnet- feld
bewegt. 3. Fall:
die Leiterschleife wird im Magnetfeld deformiert, also die Fläche
vergrößert oder verkleinert. Folgende Videos zeigen alle drei Fälle: 1.Video: Fall 1. und 2. werden gezeigt:
2.Video: der 3. Fall wird hier gezeigt
Man erkennt sofort, dass es im Video Nr.1 nur zu einer Spannungsan- zeige kommt, wenn sich die Flachspule aus dem Magnetfeld heraus- oder hineinbewegt. Eine Bewegung innerhalb des Magnetfeldes führt zu keiner Induktionsspannung. Die Größe der Spannung hängt von der „Schnelligkeit“ (Geschwindigkeit) der Bewegung ab. Je höher die Ge- schwindigkeit ist, umso größer wird die Spannung. Im dritten Fall ergibt sich bei Vergrößerung oder Verkleinerung der Leiterschleifenfläche eine Spannung, die ebenfalls von der „Schnellig- keit“ der Veränderung abhängt. Hinweis
für die Gestaltung der Experimente (Lehrer): Im
Allgemeinen wird ein Quadermagnet in der Physiksammlung nicht zur Verfügung
stehen, deshalb
kann man auch einen Hufeisenmagneten oder eine Helmholtzspule
benutzen. ( s.
hierzu Video 3 ,
Video 4 und
Video 5 von der
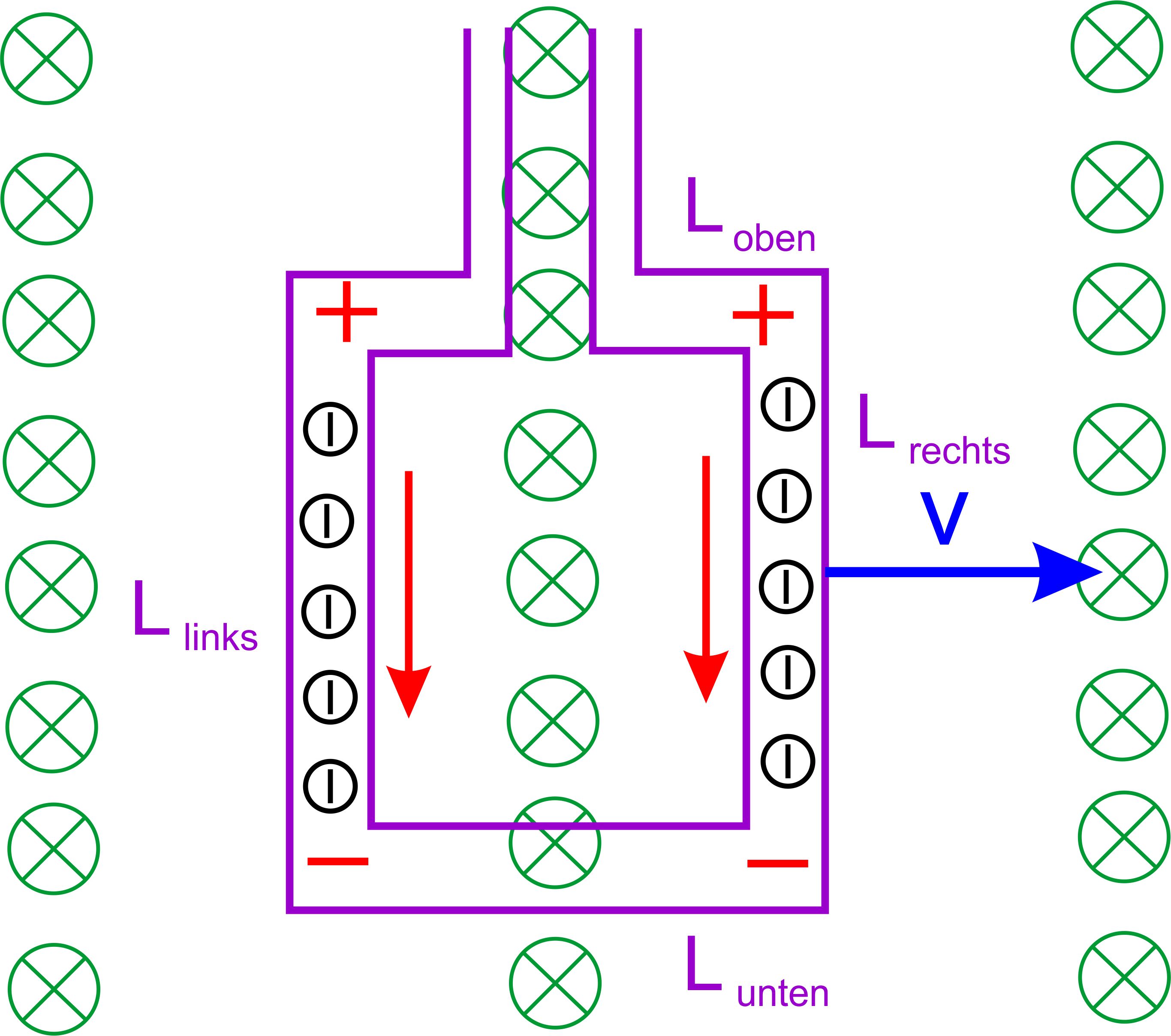
Videoliste) Zur Erläuterung sollen folgende Abbildungen dienen. Im Wesentlichen wird es um die Lorentzkraft gehen. 1. Fall: Leiterschleife vollständig im Magnetfeld
Hinweis: im oberen und unteren Leiterteil treten zwar auch
Lorentzkräfte auf, die die Elektro- nen aber nicht entlang des Leiters
verschieben. Die Ladungsunterschiede treten an den Wänden des Leiters auf (eine Art Halleffekt). Wir haben
übrigens eine ähnliche Erläuterung schon bei der Drehung
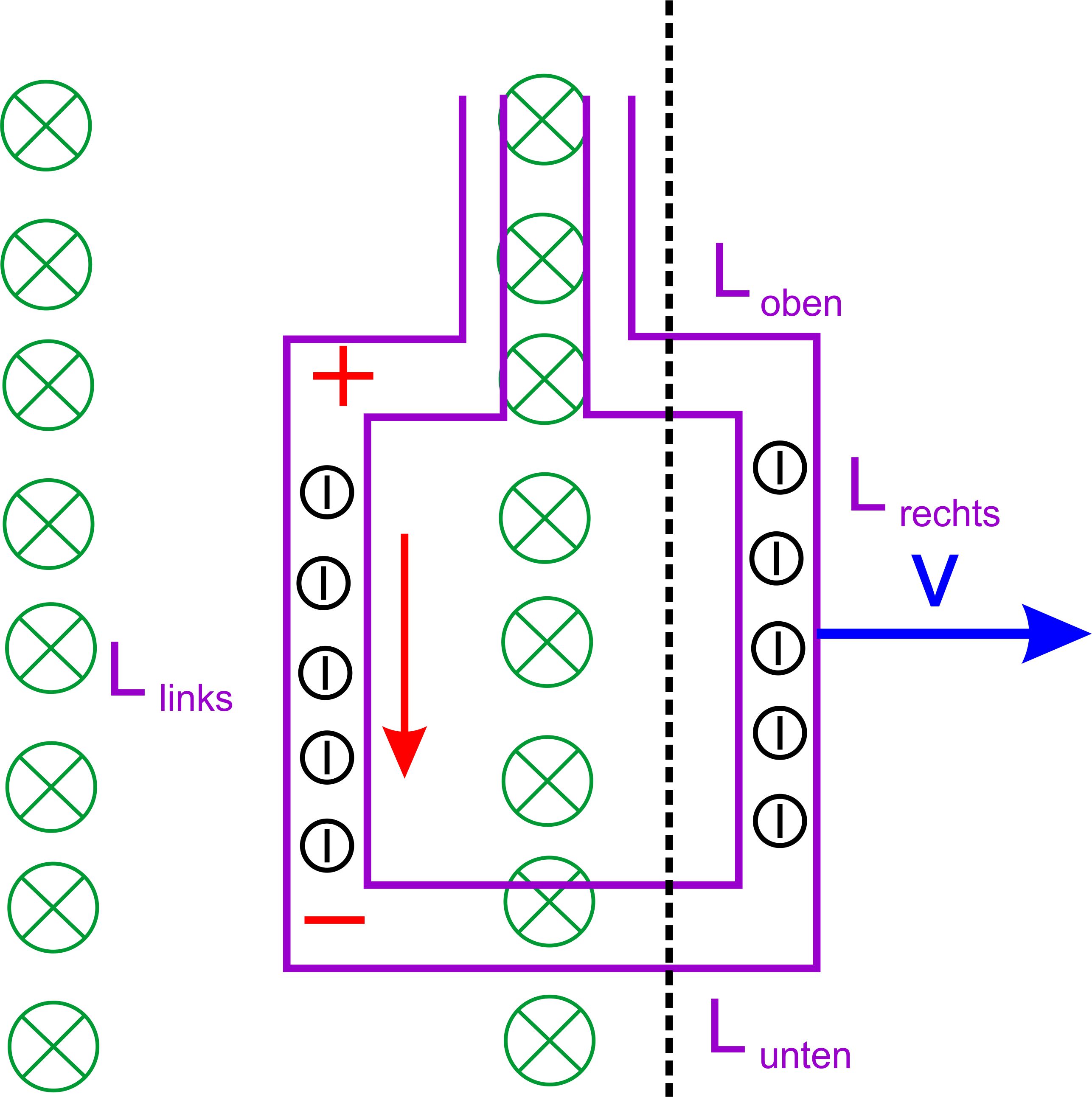
einer Leiterschleife im Magnetfeld vorgenommen. 2. Fall: Leiterschleife aus oder in das Magnetfeld bewegen
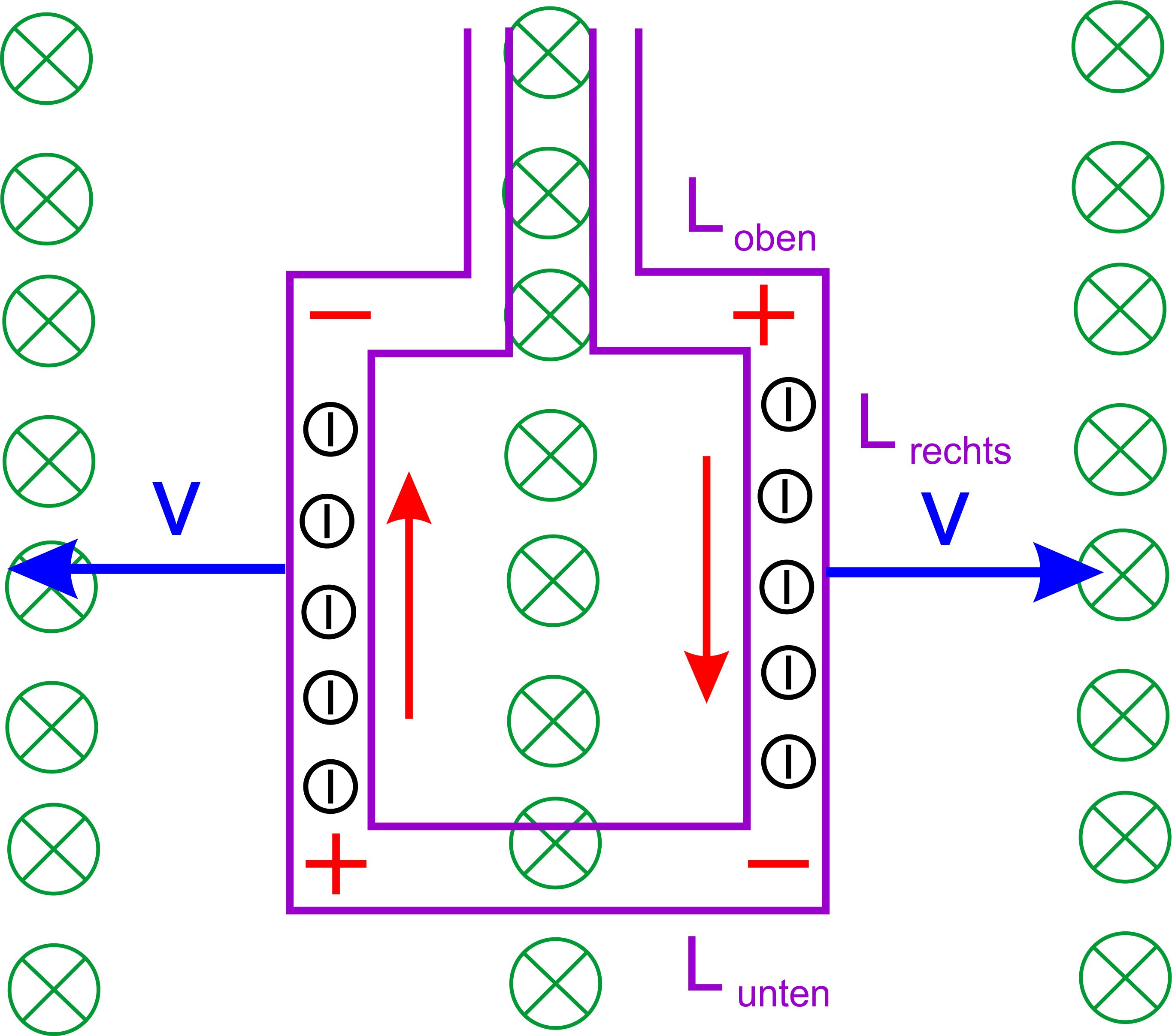
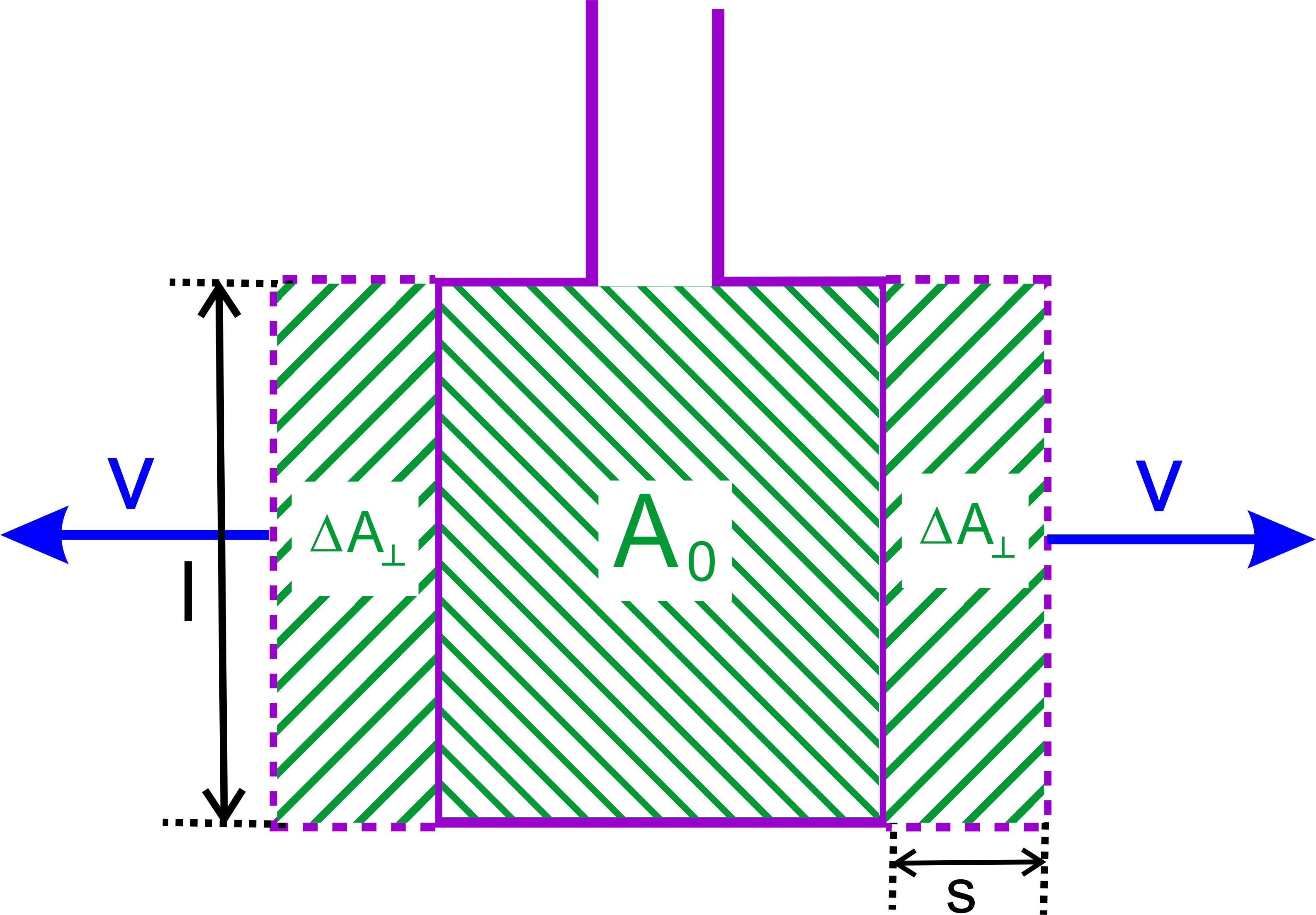
3. Fall: Deformation einer Leiterschleife im Magnetfeld
Schauen
wir uns nun an, wie wir die Induktionsspannung berechnen können. Die
Abbildungen sind hierfür ohne Magnetfeld dargestellt. Das Ma- gnetfeld
soll immer in die Papierebene hineinzeigen.
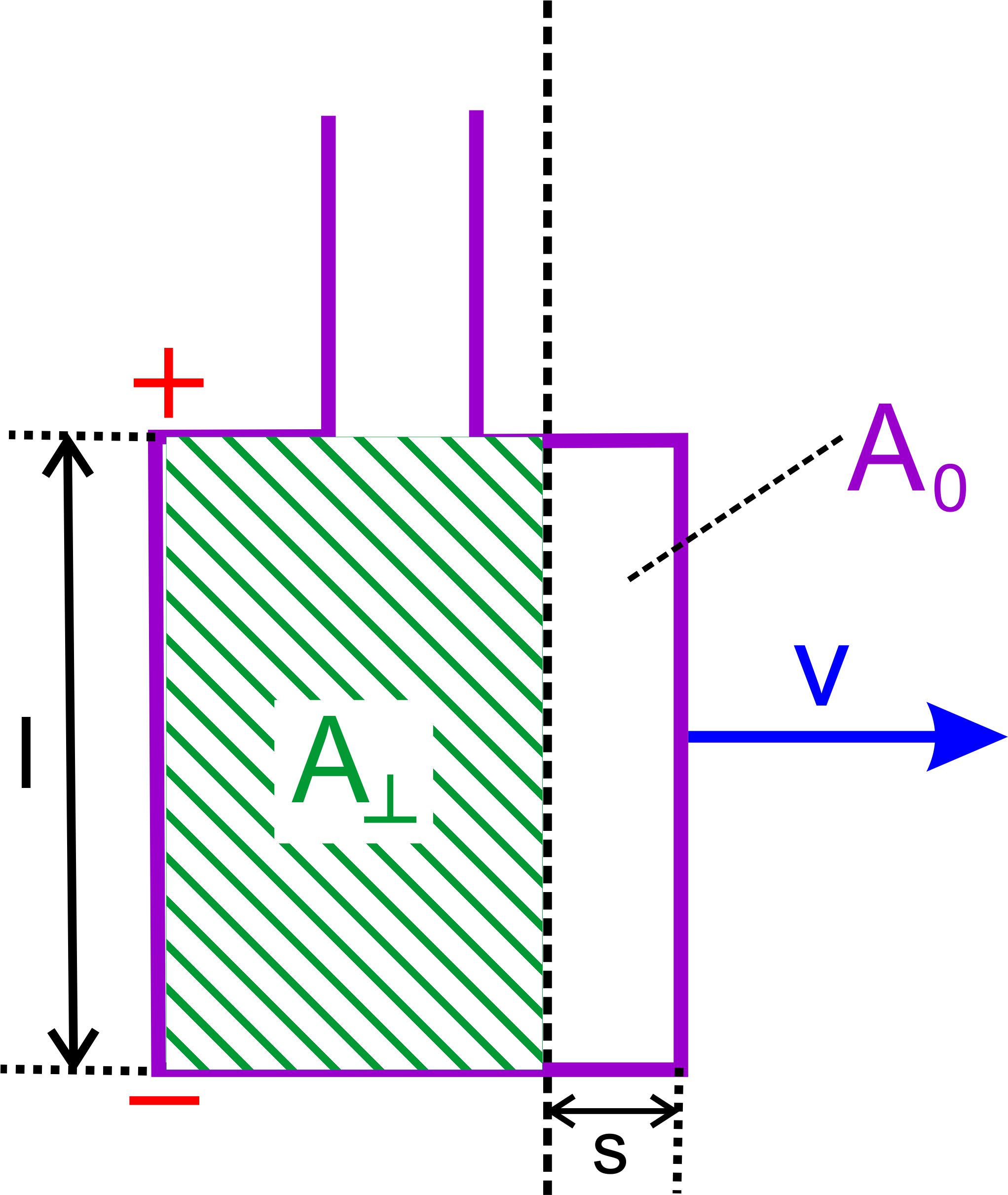
Eine alternative Herleitung geht über Fläche AꞱ, wobei AꞱ die Fläche der Leiterschleife ist, die senkrecht von Magnetfeldlinien durchsetzt wird. Mit Hilfe dieser Herleitung gelangt man dann zur allgemeinen Formel für die Induktionsspannung.
Hier taucht auch korrekterweise das Minuszeichen auf, welches sich dadurch ergibt, dass die Induktionsspannung immer einer schon vor- her angelegten Spannung entgegenwirkt (s. Selbstinduktion). 3. Fall
Man sieht also, dass sich die Induktionsspannung aus dem Produkt
„magnetische Feldstärke ∙ zeitliche Änderung von AꞱ“ ergibt. Haben wir eine Spule mit „n“-Leiterschleifen, haben wir „n“-mal die „einfache“ Induktionsspannung und müssen den Faktor „n“ noch in die Formel einbringen.
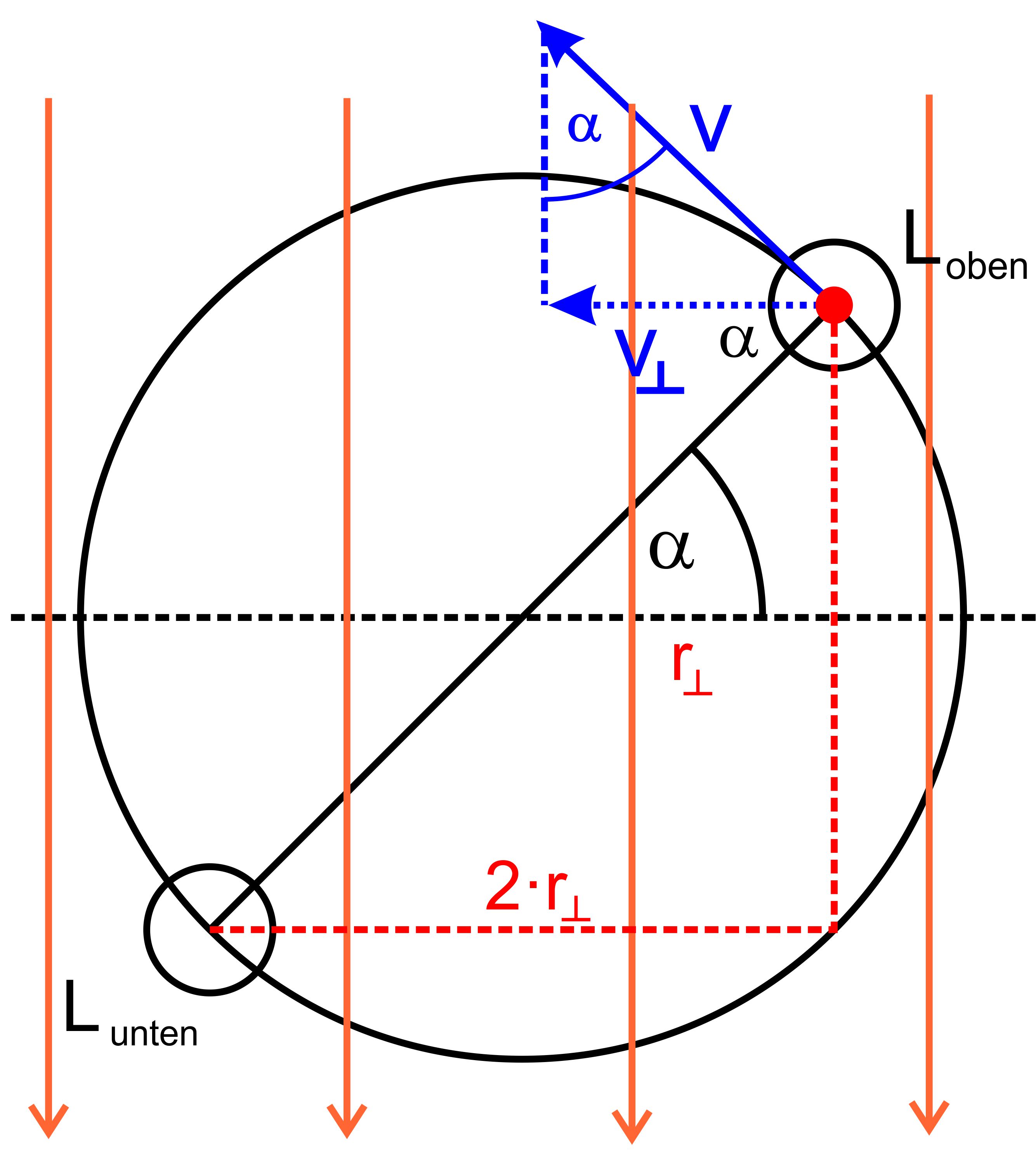
Rückblick: Drehung einer Leiterschleife Wir schauen jetzt noch einmal zurück auf das Kapitel „Flächen-änderung durch Drehung“. Können wir auch in diesem Fall die gerade hergeleitete Formel benutzen? Hierzu noch einmal zur entsprechenden Abbildung aus dem Kapitel.
Man sieht von vorne, also in Richtung der Drehachse, auf den Aufbau.
Wir erhalten also dieselbe Formel wie durch die Herleitung aus der Lorentzkraft. Somit haben wir die Formel für Uind noch einmal be- stätigt. Übungsaufgabe
sehr zu
empfehlen ist hier das Video Nr. 6
von Benno Köhler zurück zu: zum Kapitel: zum
nächsten Kapitel:
zur Übersicht: Induktion |