|
gehe zu: Induktionsgesetz−1.Teil−Kapitel 2 Im vorherigen Kapitel zum Induktionsgesetz
haben wir für die Drehung einer Spule
im Magnetfeld eine Formel für die Induktionsspannung hergeleitet.
Er ergab sich
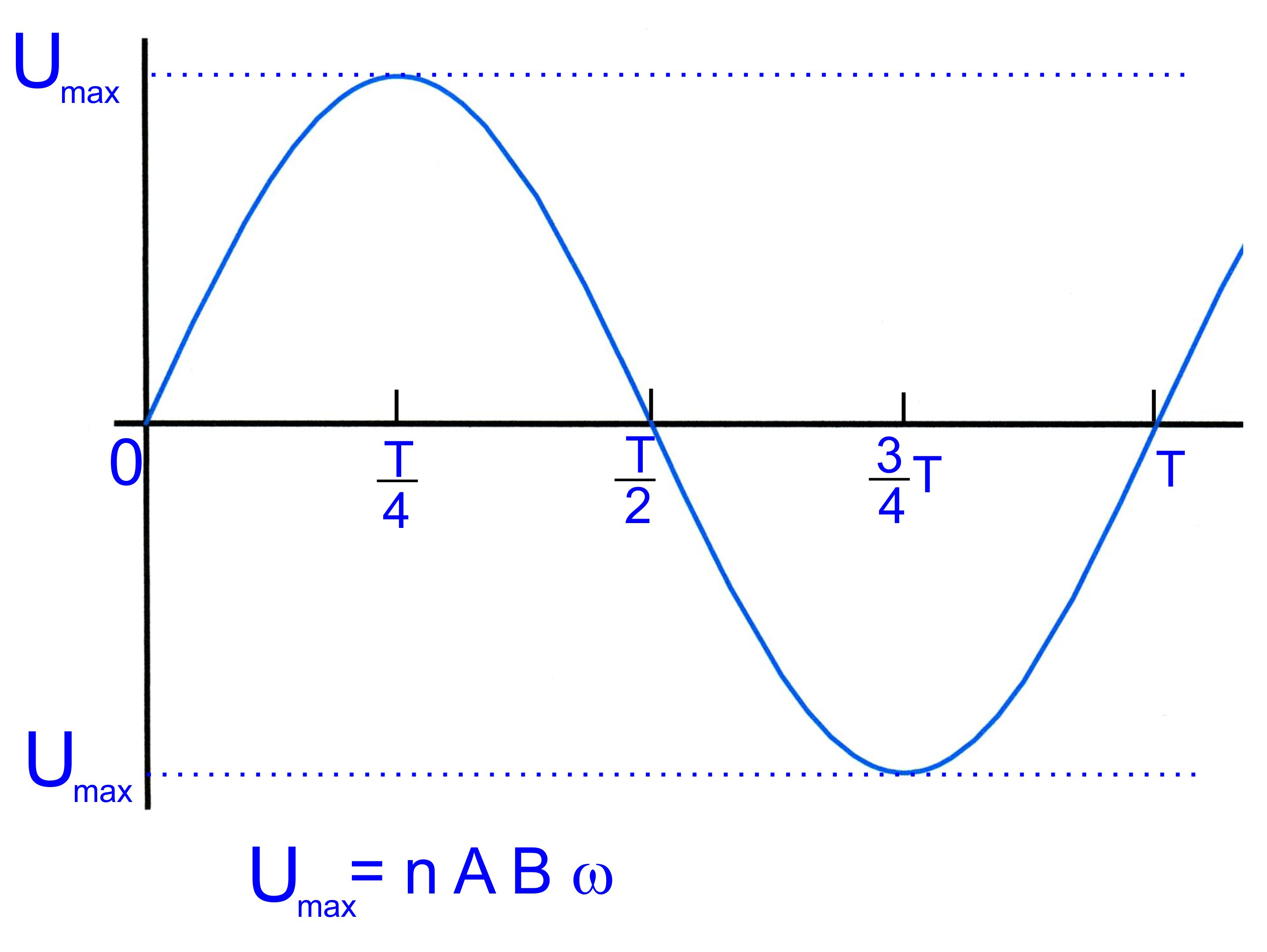
Das Aussehen wird im Wesentlichen durch den zeitlich veränderlichen Term sin(ω∙t) bestimmt. Es liegt eine Sinuskurve vor. Wir haben also folgenden Graphen.
Die Spannung wechselt somit die Polung und schwankt zwischen den Maximalwerten von Umax = n∙A∙B∙ω, da der Sinus den Maximalwert 1 annehmen kann. Man startet bei dem obigen Verlauf bei t = 0 s, wenn ω∙t = 0 ist, also muss die Leiterfläche senkrecht von den Magnetfeld- linien durchsetzt werden (s. 1. Kapitel). Bei T/4 liegt die Leiterfläche parallel zu den Feldlinien. Die Frequenz im deutschen Netz beträgt 50 Hz. Die Schwingungs- dauer T hat also damit den Wert 0,02 s. Angeschlossene Geräte wer- den somit die ganze Zeit mit unterschiedlichen Spannungswerten und damit auch Stromstärken versorgt. Dies kann z.B. bei Leuchtmitteln, insbesondere LED-Leuchten, zu Lichtflimmern führen, welches durch entsprechende elektronische Verschaltungen, z.B. Dioden und Glät-tungskondensatoren, verhindert werden muss.
Stromstärke Befindet sich im Stromkreis nur ein ohmscher Widerstand entspricht der Verlauf der Stromstärke dem der Wechselspannung. Mit R=U/I ergibt sich für I = U/R, also haben wir für den Stromstärke- verlauf folgenden Term.
Effektivwerte Im Alltag wird der Wert der Wechselspannung des Hausnetzes immer mit 220 V (bzw. 230 V) angegeben. Man gibt also gar keinen schwankenden Wert zwischen zwei Maxi- malwerten an! Was hat diese Alltagsangabe zu bedeuten? Es handelt sich um den sogenannten Effektivwert der Wechselspan- nung. Es gilt folgende Festlegung des Effektivwertes:
Die Definition gilt natürlich entsprechend für die effektive Stromstärke. Bei einem Wechselstrom haben wir natürlich nicht nur eine sich än-dernde Spannung bzw. Stromstärke, sondern auch eine schwankende Leistung, da sich diese aus den beiden Größen ergibt. Mit U(t) = Umax ∙
sin(ωt) und I(t) = Imax
∙ sin(ωt) ergibt sich P(t) = U(t) ∙ I(t)
= Umax ∙ Imax
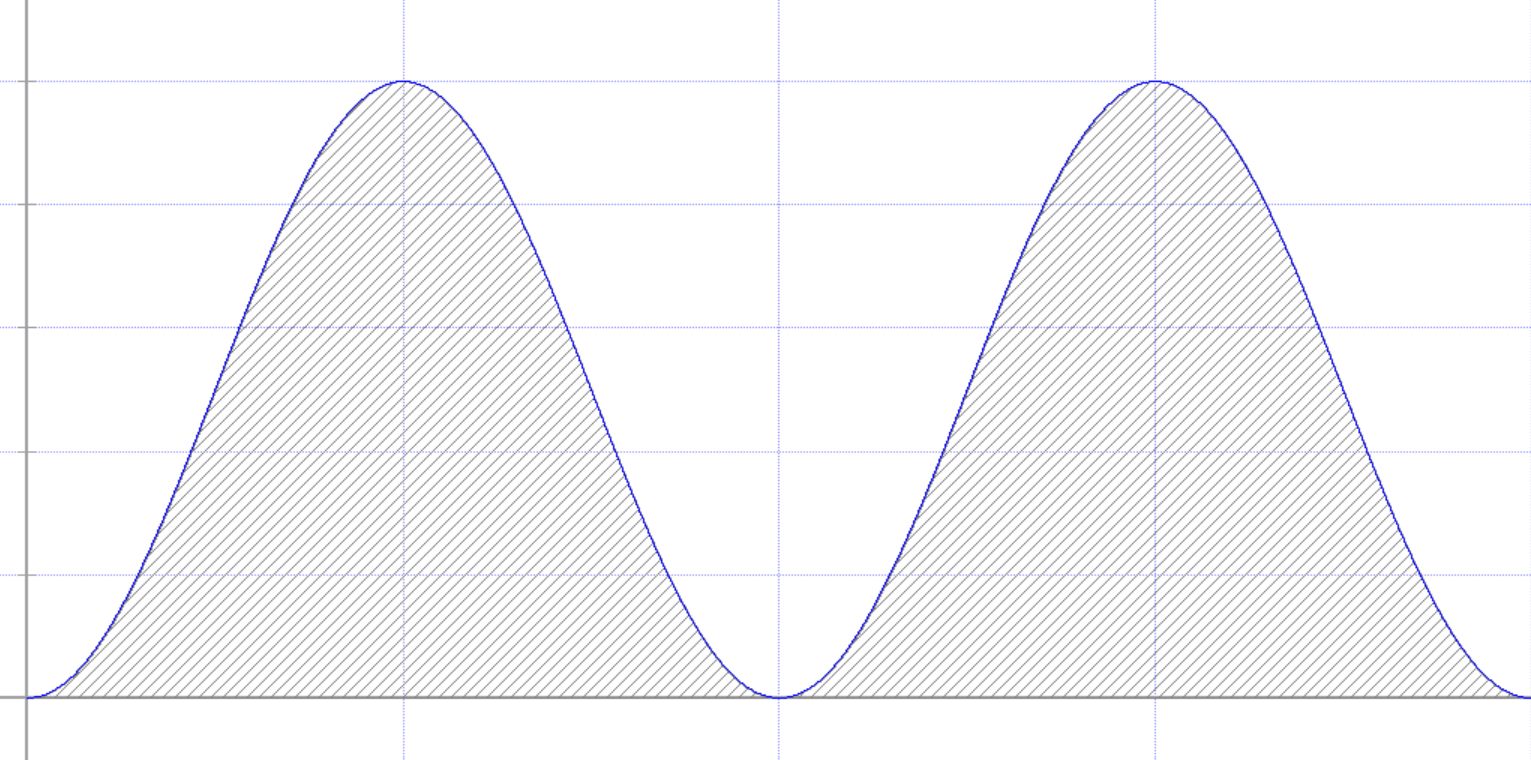
∙ sin2(ωt) = Pmax ∙ sin2(ωt) Der Graph dieser Funktion hat dabei folgendes Aussehen:
Man sieht sofort, dass die Leistung laufend zwischen 0 und Pmax schwankt. Es wird also keine kontinuierliche Leistung am Widerstand abgegeben. Daher ist es interessant so etwas wie die mittlere Leistung herauszufinden. Diese mittlere Leistung würde durch eine entsprech- ende effektive Spannung bzw. Stromstärke aufgebracht werden. Effektivwerte bestimmen –
Einführung Schauen wir
uns zunächst ein einfaches Beispiel für die Leistung an. 1. Fall:
die Leistung ist über den Zeitraum T konstant
Dann ist
natürlich klar, dass dann die mittlere Leistung der konstanten Leistung
entspricht. Die Fläche unter dem Graphen entspricht dabei der am
Widerstand verrichteten Arbeit bzw. der zur Verfügung ge- stellten
Energie. 2. Fall:
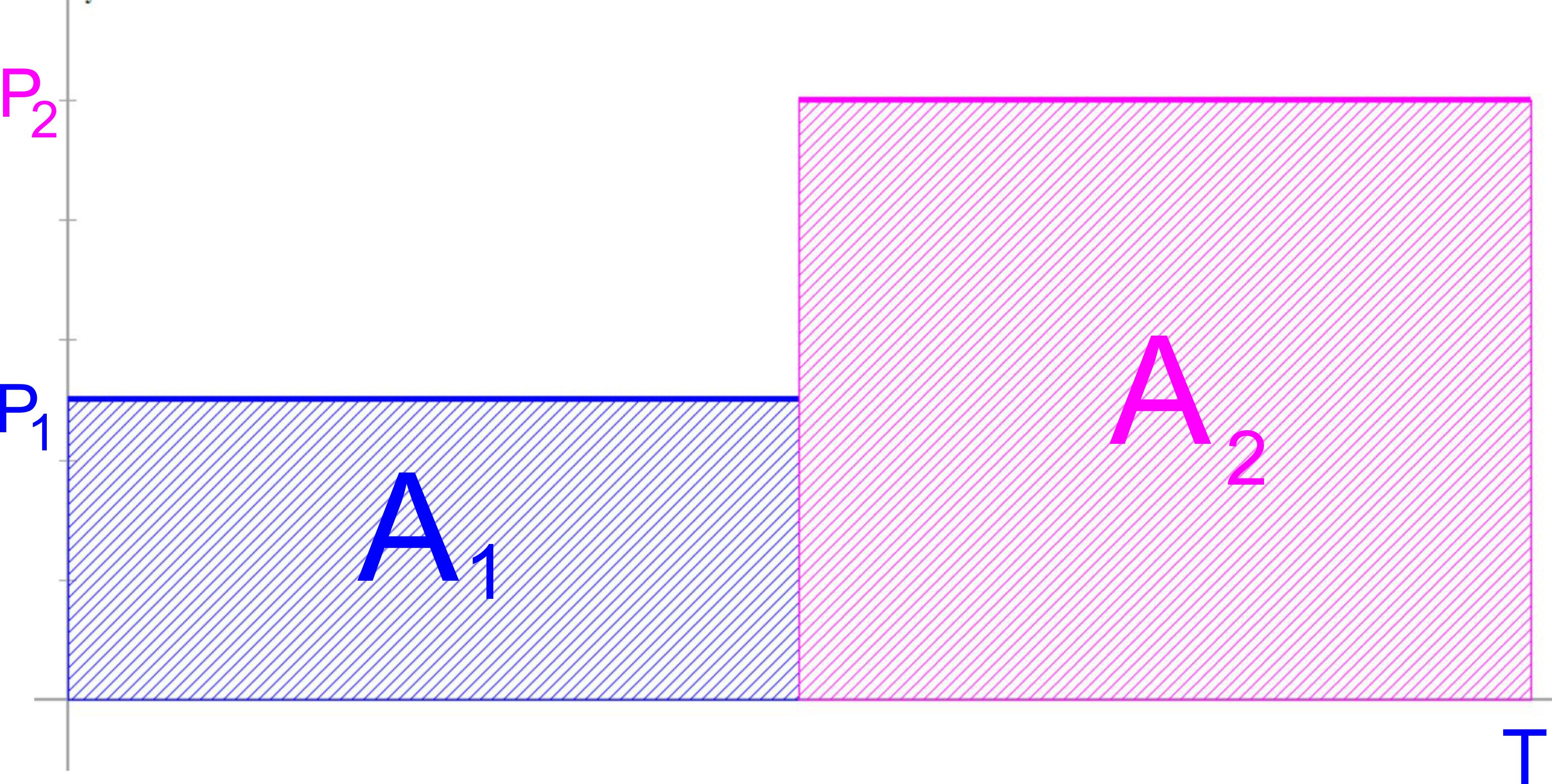
die Leistung ist in verschiedenen Zeiträumen unterschiedlich groß
Am Anfang ist die Leistung gering. Es wird wenig Arbeit verrichtet. Die Fläche A1 ist klein. Danach gibt es einen Zeitraum mit großer Leistung. Es wird viel Arbeit verrichtet. Die Fläche A2 ist
groß. Man
sucht jetzt die mittlere Leistung, d.h. die konstante Leistung, die auf
Dauer die gleiche Arbeit verrichtet wie die beiden unterschiedlich- en
Leistungen. Man muss
also eine Fläche Aeff finden, die über den
ganzen Zeitraum einer
Rechteckfläche entspricht, die
denselben Flächeninhalt wie die beiden
getrennten Flächen aufweist.
Diese Leistung Peff
ist also gesucht und entspricht der
mittleren Leis- tung. Es geht also letztendlich um eine Flächenbestimmung. Also sind tungsfunktion. Effektivwerte bestimmen – Wechselspannung Schauen wir uns noch einmal den konkreten Fall der Wechselspan- nung an.
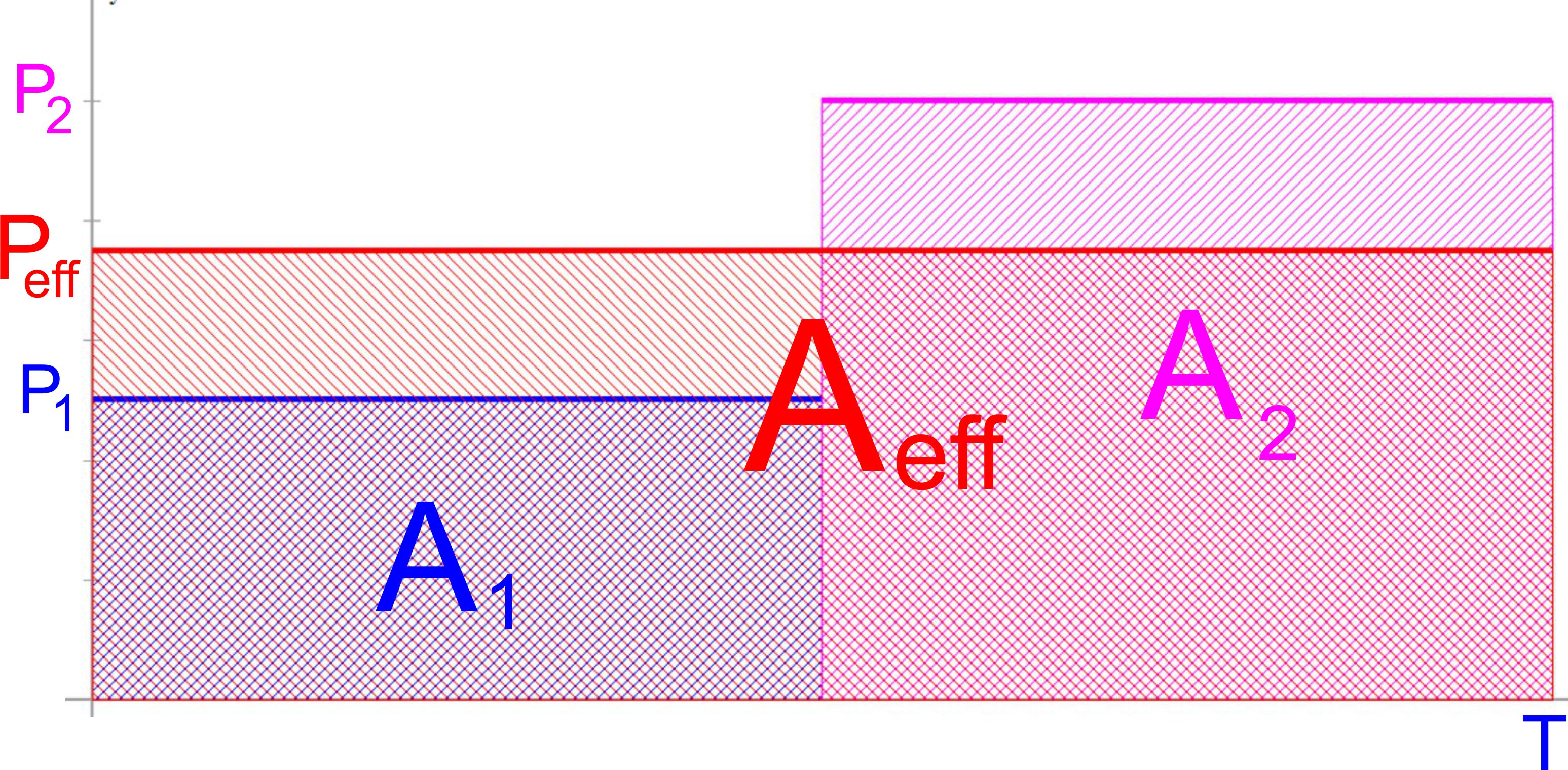
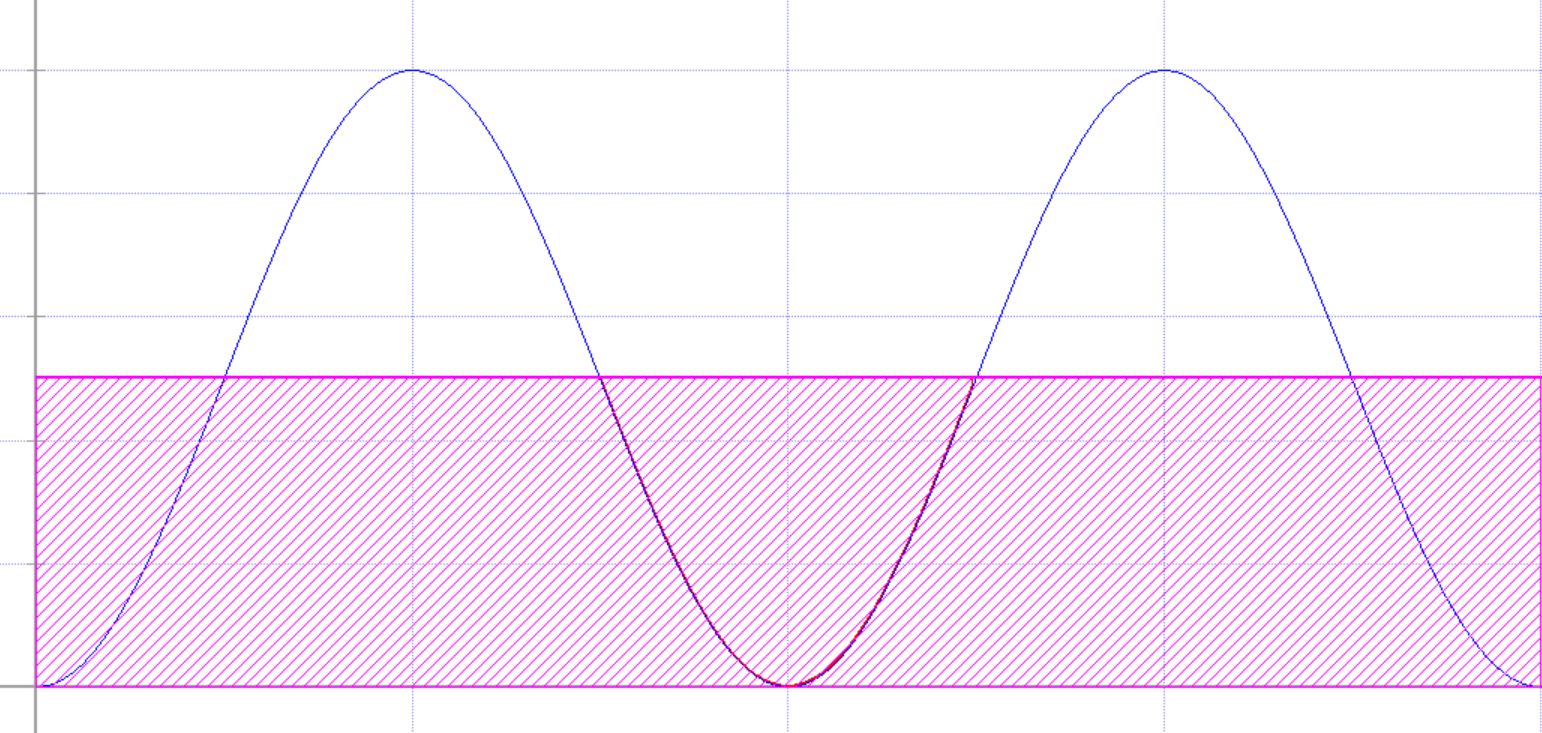
Man sucht jetzt also ein Peff, so dass mit diesem Peff eine Rechteck- fläche entsteht, die denselben Wert wie die Fläche unter dem Graphen aufweist.
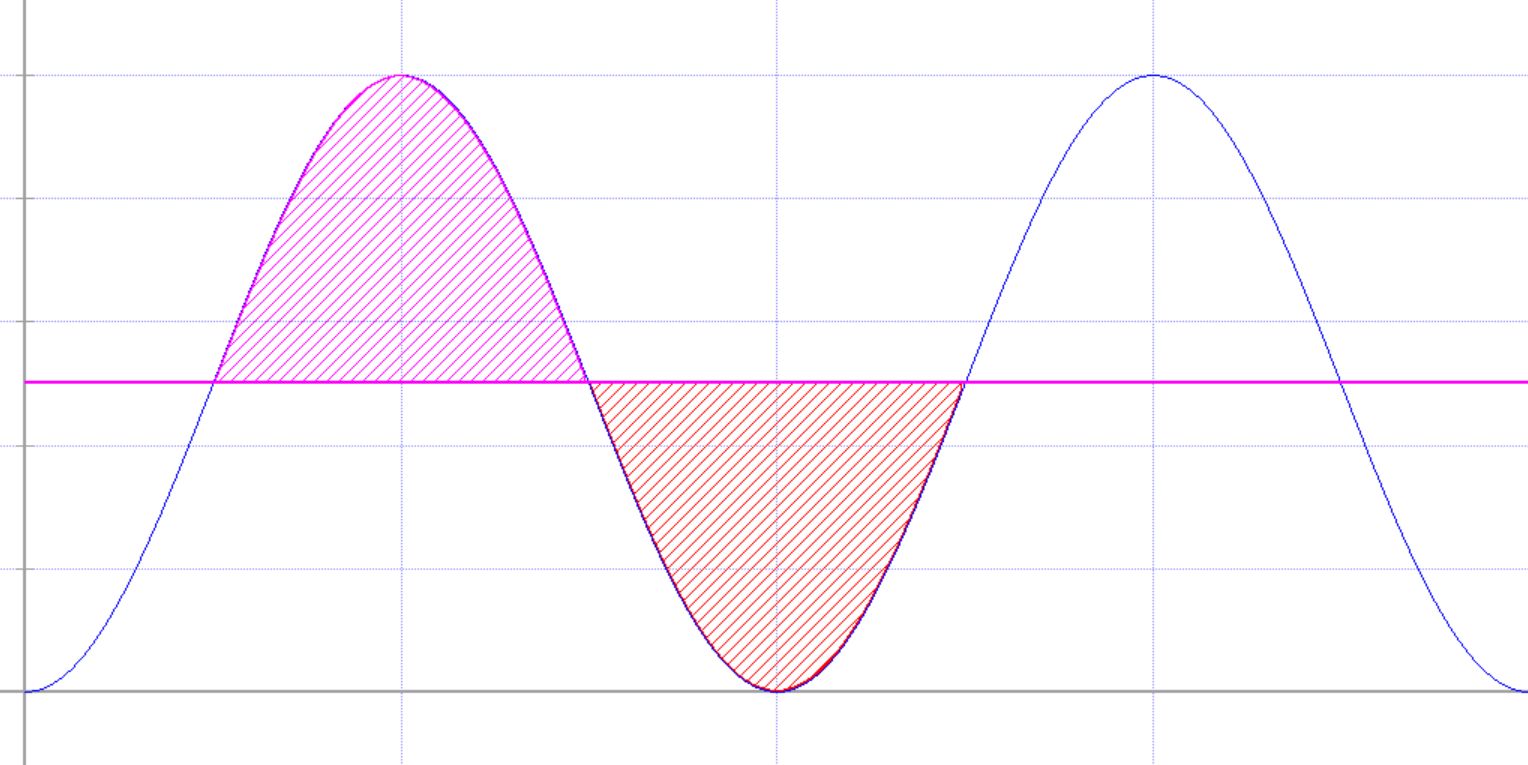
Wenn man eine Linie auf der Hälfte von Pmax zieht, sieht es so aus, dass die schraffierte violette Fläche der rot schraffierten Fläche ent- spricht, so dass das gesuchte Rechteck folgende Aussehen hat.
Peff wäre somit die Hälfte von Pmax. Hinweis:
1.) Wenn
man die Behauptung genau nachprüfen will, kann man den Graphen einmal auf Papier
zeichnen lassen. Dann schneidet man den oberen Teil des Hügels aus und sieht,
dass er genau
in das untere Tal passt. oder: 2.) Ich habe einmal mit GeoGebra die Flächen bestimmt und man sieht, dass der betrags- mäßig oder: 3.) Es gibt auch einen Exkurs in die Mathematik. Hier wird einerseits
mittels Additionstheorem und anderseits mittels Integral das Ergebnis noch einmal bestätigt
(leider noch in Arbeit).
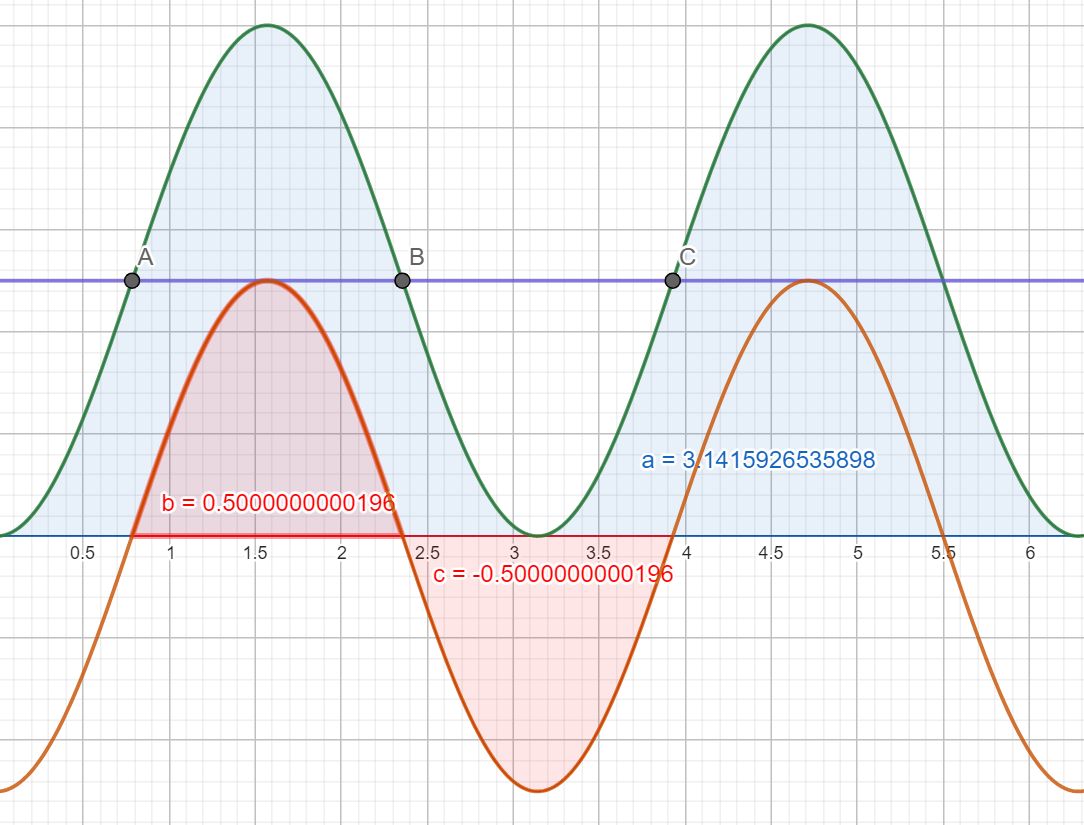
Im
Koordinatensystem mit P = 1 und T = 2∙π erhält man für die blaue
Fläche berechnet von GeoGebra
a = π, was man auch erhält, wenn man Peff
= 0,5 mit 2∙π multipliziert, wie man es bei der
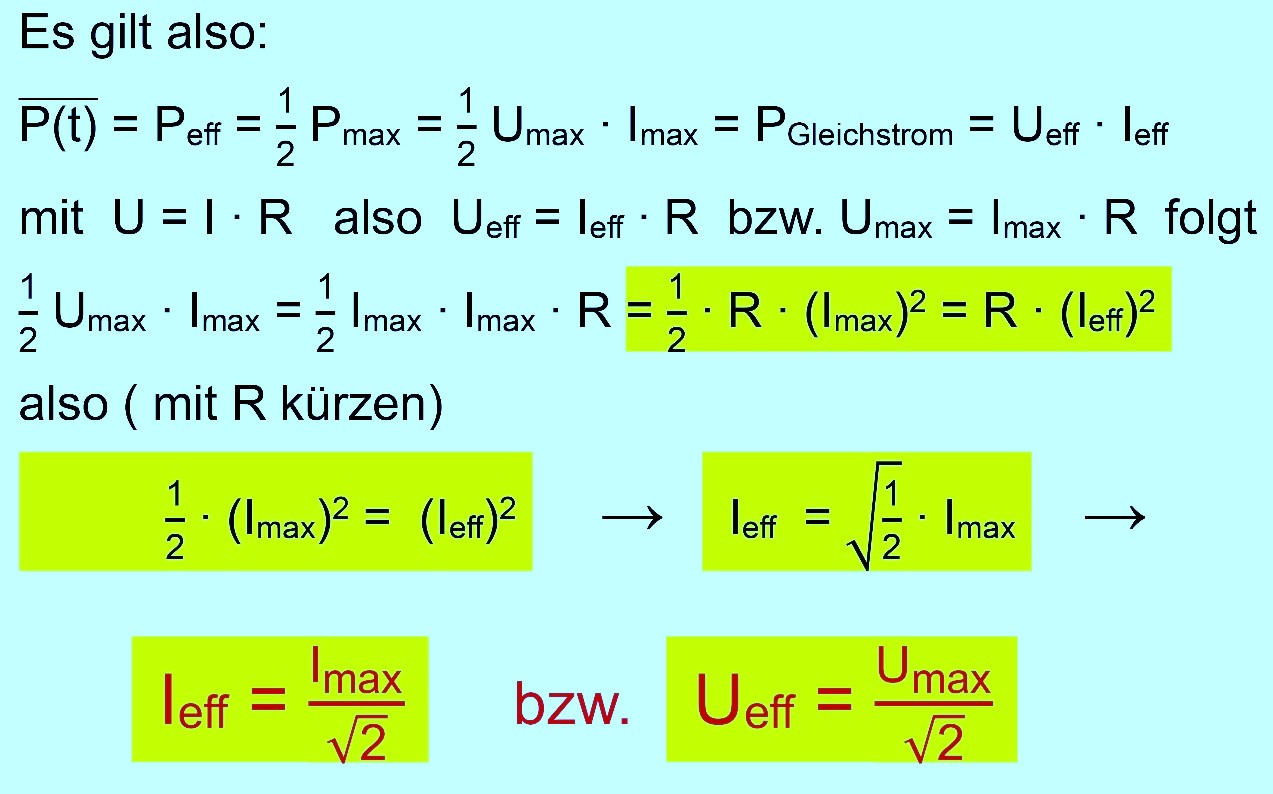
Rechteckfläche machen müsste. Für die Effektivwerte von Spannung und Stromstärke ergibt sich dann folgende Herleitung.
Wenn man also heute in Deutschland von einem Effektivwert der Spannung von 230 V ausgeht, ergibt sich mit der Formel
eine Maximalspannung von 325 V. Der Wechselstrom schwankt also immer zwischen +325 V und −325 V. zurück
zu: zum vorherigen Kapitel zur
Übersicht: |



%201%20verlauf.jpg)