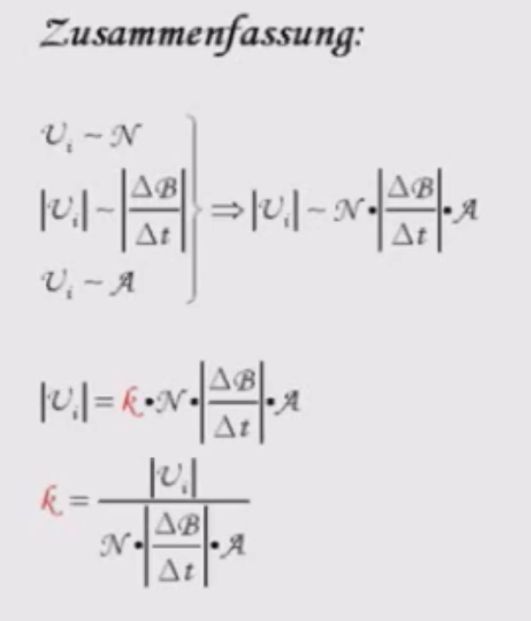|
gehe zu:
Induktionsgesetz−2.Teil Änderung der magnetischen Feldstärke Bisher haben wir uns mit der Entstehung einer
Induktionsspannung durch Flächenänderung beschäftigt, wobei die
Flächenänderung durch Bewegung
stattfinden muss. Damit lässt sich diese Span- nungserzeugung
über das Auftreten der Lorentzkraft
erklären. Es gilt folgender Zusammenhang:
In diesem Kapitel geht es jetzt um das Auftreten
einer Induktionsspan- nung
ohne Bewegung. Wir haben keine Möglichkeit auf alte Kenntnis- se
zurückzugreifen, sondern müssen dies als neuen physikalischen Zusammenhang akzeptieren. Wir sehen uns die Erzeugung einer Induktionsspannung
ohne Be- wegung
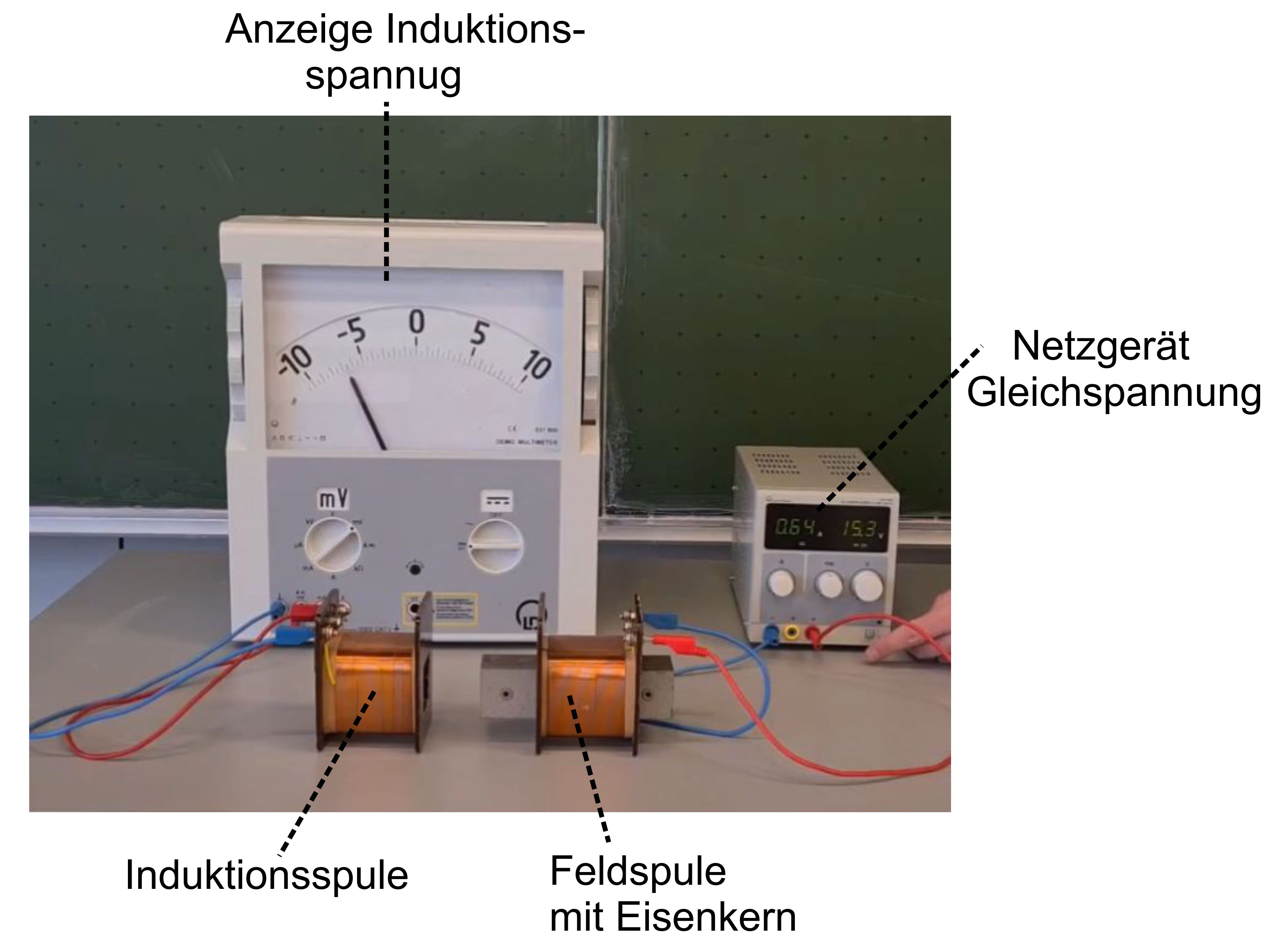
zunächst im Experiment an. 1. Anordnung: Hier meine experimentelle Anordnung im Bild
Aufbau: das Magnetfeld wird über zwei in Reihe
geschaltete Spulen erzeugt. Diese Spulen sitzen auf einem Hufeisenjoch
und werden oben durch Polschuhe abgeschlossen. Zwischen diesen
Polschuhen wird eine Leiterschleife eingeklemmt, die als
Induktionsspule dient. Die Feldspule wird über ein Gleichstrom-Netzgerät
mit Strom versorgt. Die Induktionsspannung wird an einem Voltmeter in
Mittelstellung ab- gelesen. Über einen Schalter kann die Stromzufuhr zu
den Feldspulen unterbrochen werden. Versuchsablauf: bei Betätigung des Schalters tritt
kurzfristig beim Ein- und Ausschalten ein Spannungsstoß auf. Die Spannung
ist dabei ent- gegengesetzt gerichtet. Hierzu folgendes Video: Quelle:
Video wurde von T. Imkamp am SG Gt aufgenommen 2. Anordnung In dieser Anordnung werden zwei Spulen
nebeneinandergestellt, wo- bei beide oder eine Spule einen Eisenkern aufweist.
Hierzu liegen im Folgenden zwei Videos der Anordnungen vor. Im ersten Fall wird der Feldstrom ein- und
ausgeschaltet, im zweiten Fall wird der Feldspule eine niederfrequente
Wechselspannung zuge- führt.
Exakte
Auswertung durch Experiment Exakte Auswertungen sind mit komplexeren Aufbauten
möglich. Meine Recherche ergab, dass dies vor allem durch Benno
Köhler im Internet stattfindet. Daher im Folgenden Ausschnitte aus
seinem Video hierzu. Zunächst zum Aufbau:
kurze Erläuterung: Eine große Zylinderspule wird als Feldspule benutzt,
d.h. in dieser Spule wird das Magnetfeld erzeugt. Hierzu muss die
Spule an eine Spannungsquelle (Dreiecksgenerator) angeschlossen
werden. Die Stromstärke in der Feldspule wird an einem Messgerät
angezeigt. In diese Feldspule werden verschiedene kleinere
Induktionsspulen eingeführt und deren Induktionsspannung gemessen. Da
die Induk- tionsspannung
gering ist, wird ein Verstärker zusätzlich benutzt. Hinweis für Lehrer: Man findet leider nicht in jeder
Sammlung einen Dreiecksgenerator oder Funktionsgenerator. Dann muss man zur Not versuchen per
Hand einen gleichmäßigen Anstieg und Abfall der Feldstromstärke zu erreichen. 1. Experiment: qualitative Auswertung bei Änderung
der Stromstärke innerhalb der Feldspule Quelle:
Ausschnitt aus Video 1
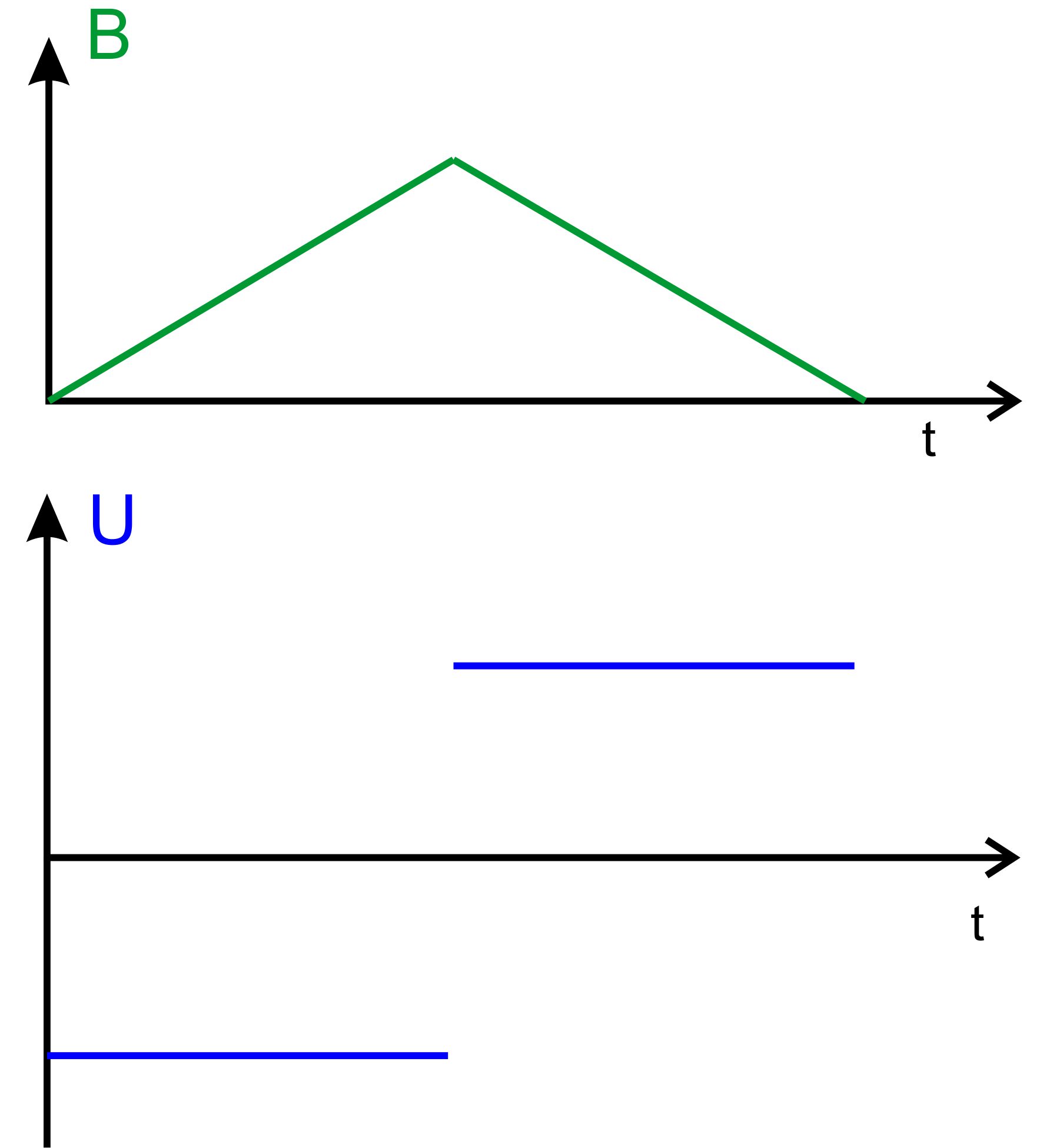
(Videoliste) Ergebnis: Der Dreiecksgenerator erzeugt einen linearen Anstieg
und Abfall der Stromstärke in der Feldspule. Damit ändert sich auch
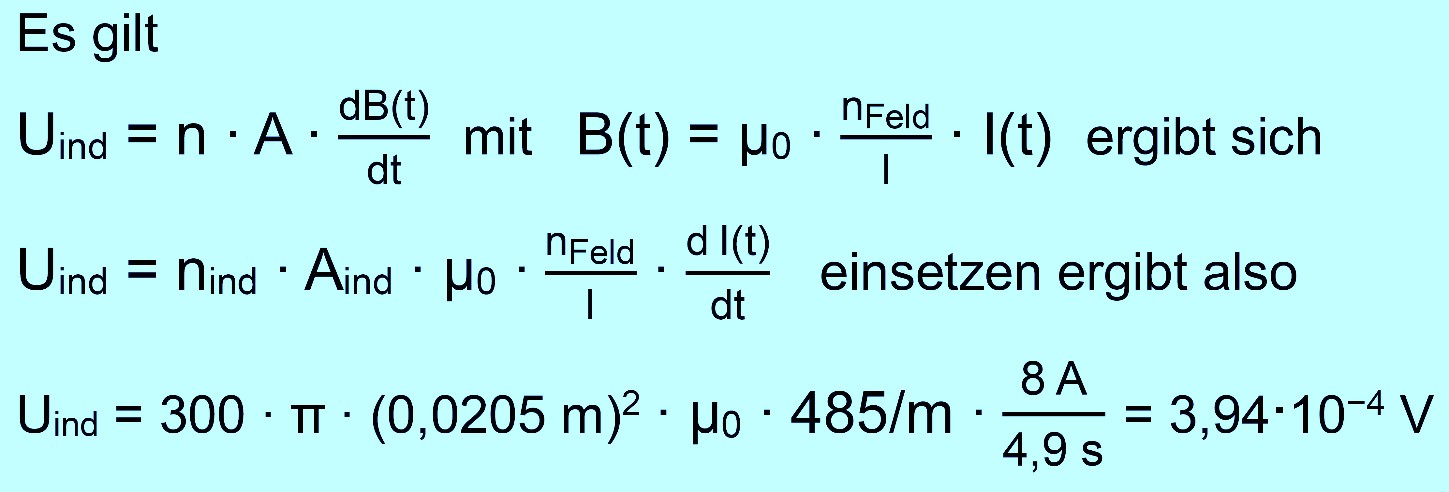
die magnetische Feldstärke in der Feldspule linear. Denn es gilt ja (s.
Kapitel „Magnetfeld“)
B(t) ist also proportional zu I(t), da alle anderen
Größen konstant blieben. Bei einer linearen
Änderung des Magnetfeldes gibt es eine konstante Induktionsspannung. Die folgende Abbildung zeigt
dies noch einmal.
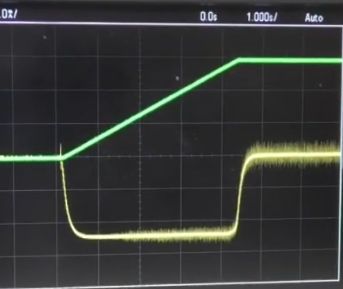
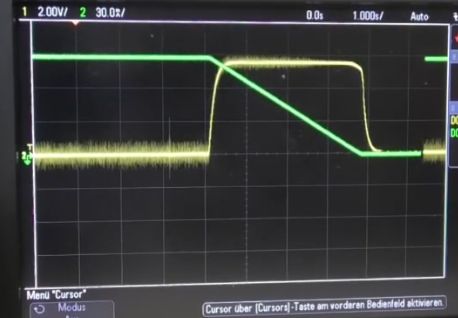
Folgende Bilder aus dem Video „Physik mit c“ (ab.
10:45) zeigen auch noch einmal die Verhältnisse:
Im folgenden Video misst Benno Köhler alle möglichen
Abhängigkeit- en durch. Quelle:
Ausschnitt aus Video 1
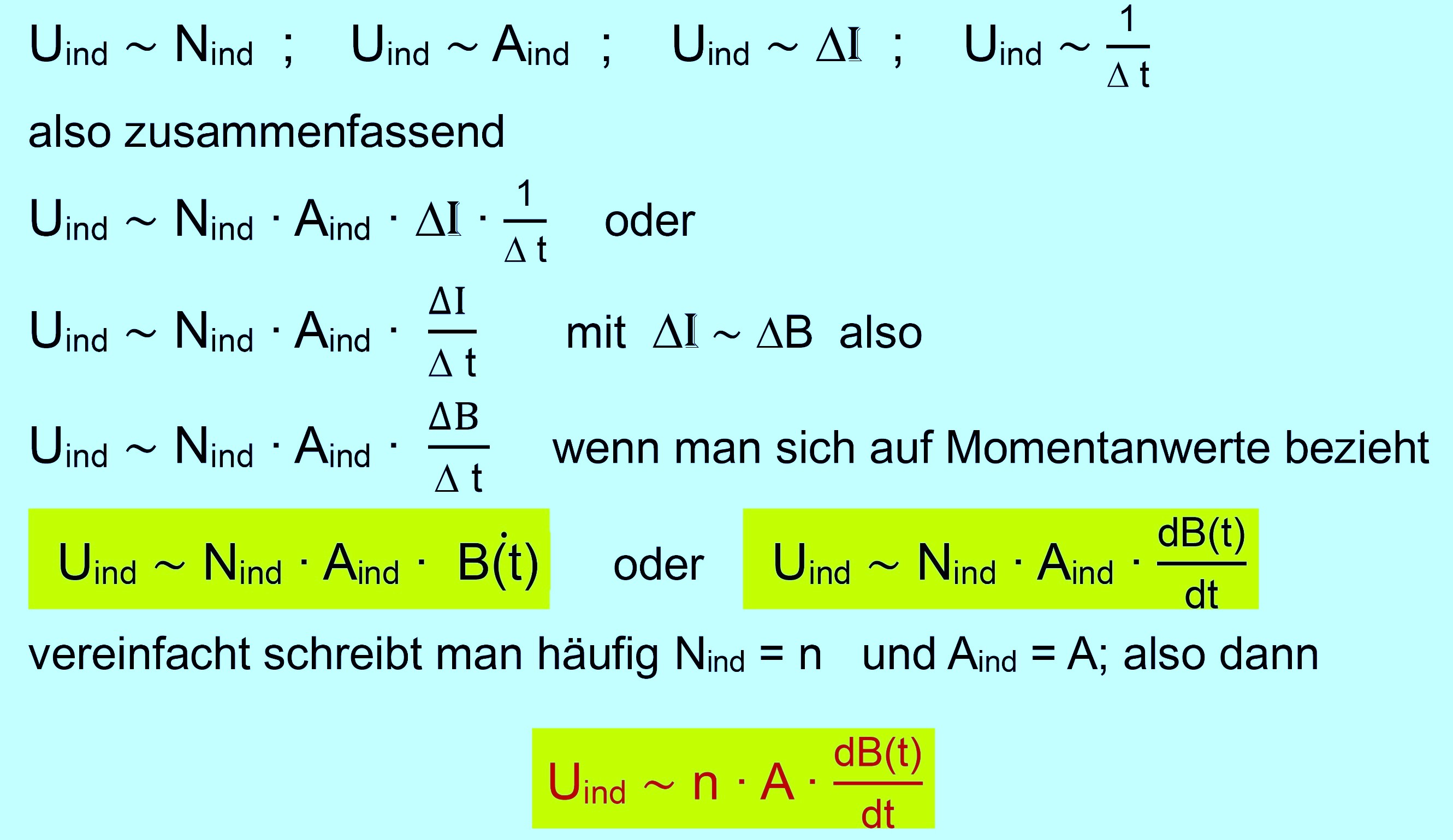
(Videoliste) Es ergeben sich
folgende Zusammenhänge:
Es bleibt jetzt nur noch die
Proportionalitätskonstante zu bestimmen. Dies macht Benno Köhler leider nicht. Hierzu kann
man aber folgende beiden Videos finden.
Man stellt fest, dass die Proportionalitätkonstante
k=1 ist
In die Formel wird das Minuszeichen eingefügt, da
die Induktions- spannung
immer einer schon vorher angelegten Spannung entgegen- wirkt (s. Selbstinduktion). Außerdem muss A durch AꞱ ersetzt
werden, was bei B. Köhler nicht nötig ist, da bei ihm durch den Versuchsaufbau A = AꞱ
ist.
gehe zu:
zurück zum Kapitel: zurück
zur Übersicht „Induktion“ |