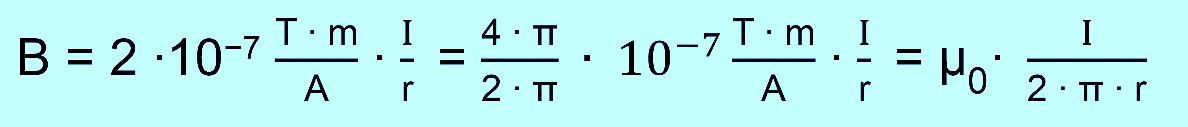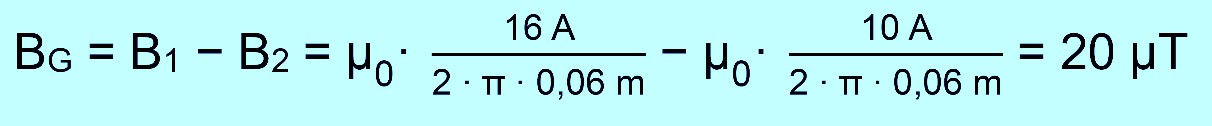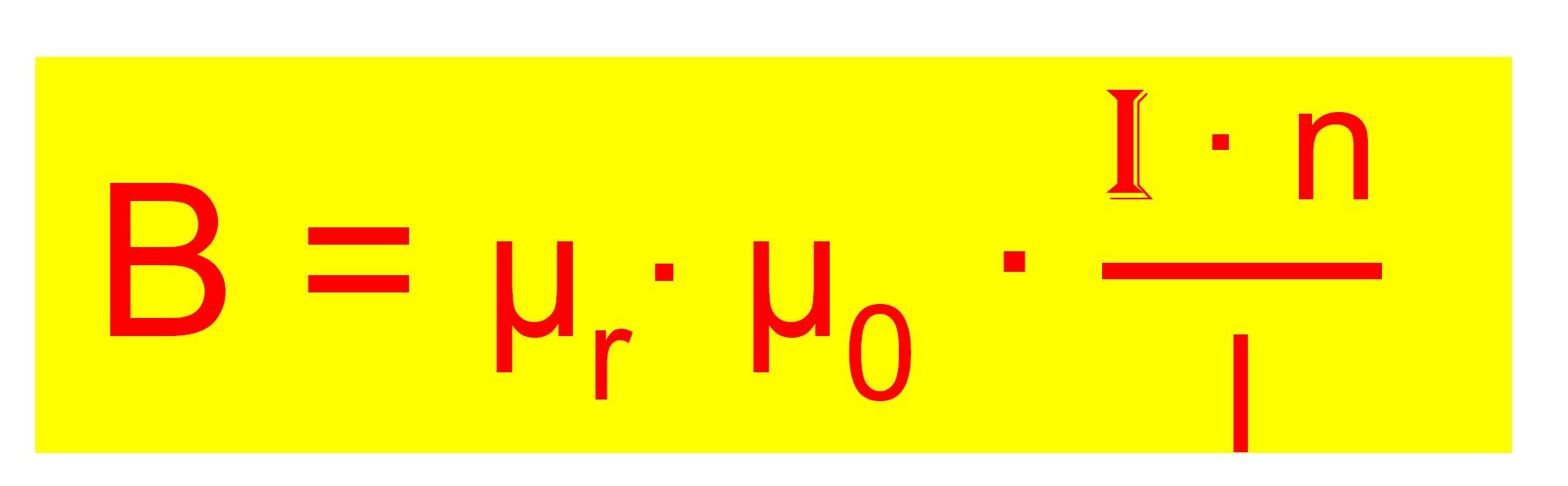|
zum Abschnitt:
Magnetfelder durch Stromfluss Einführung Neben
den schon aus der Mittelstufe bekannten Dauermagneten (Stab- und
Hufeisenmagnet) gibt es natürlich auch Magnetismus, der durch
einen fließenden Strom hervorgerufen wird. In der Mittelstufe kennt
man hier die Elektromagnete. Im Folgenden soll das Magnet- feld
verschiedener stromdurchflossener Strukturen (langer Leiter, Kreisring,
Spule) genauer betrachtet werden. Wir
sehen uns zunächst den Feldlinienverlauf der Felder an. Danach werden
noch Formeln zur Bestimmung der magnetischen Feldstärke hergeleitet. Magnetfeld
langer Leiter Verlauf der Feldlinien Der
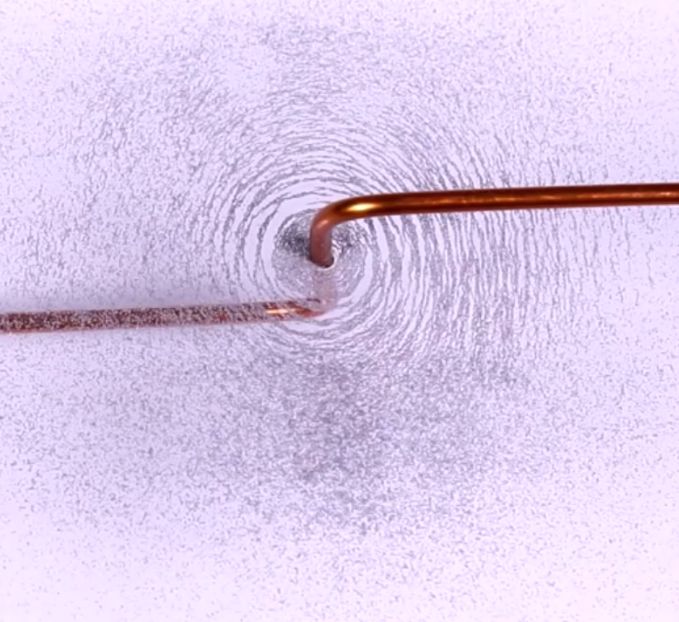
einfachste Versuch besteht darin, Eisenfeilspäne für den groben Verlauf
des Magnetfeldes zu benutzen. Will man auch über die Feldlinienrichtung
eine Auskunft bekommen, muss man Magnetnadeln in die
Nähe des langen Leiters halten. Hierzu
folgende Videos:
Hinweis: Wer den Oersted-Versuch
sehen will, sollte in der Videoliste
4.2. ansehen. Es zeigt
sich, dass das Magnetfeld konzentrische Kreise um den stromdurchflossenen,
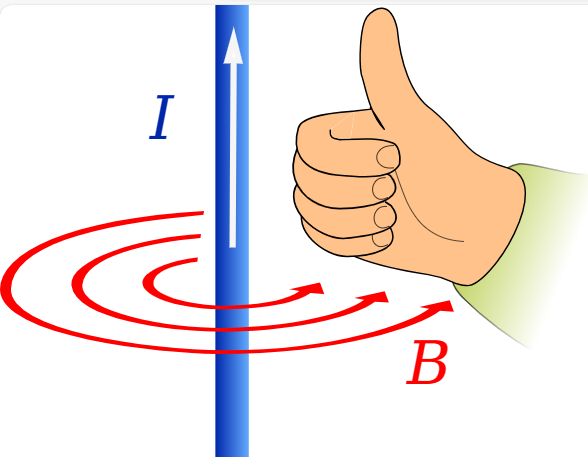
langen Leiter bildet. Die Feldlinienrichtung kann mit der
Rechte-Faust-Regel gewonnen werden. Es ist anzunehmen, dass die
Stärke des Magnetfeldes vom Abstand zum Stromleiter ab- hängt.
Die genauere Berechnungsformel folgt unten.
Formel für die Feldstärke Zum
Versuchsaufbau benötigt man einen langen, dicken Leiter oder mehrere
zu einem Bündel zusammengefasste Leiter. Die Messungen finden
mit einer Hallsonde oder mit der App „phyphox“
statt. Das Netz- gerät
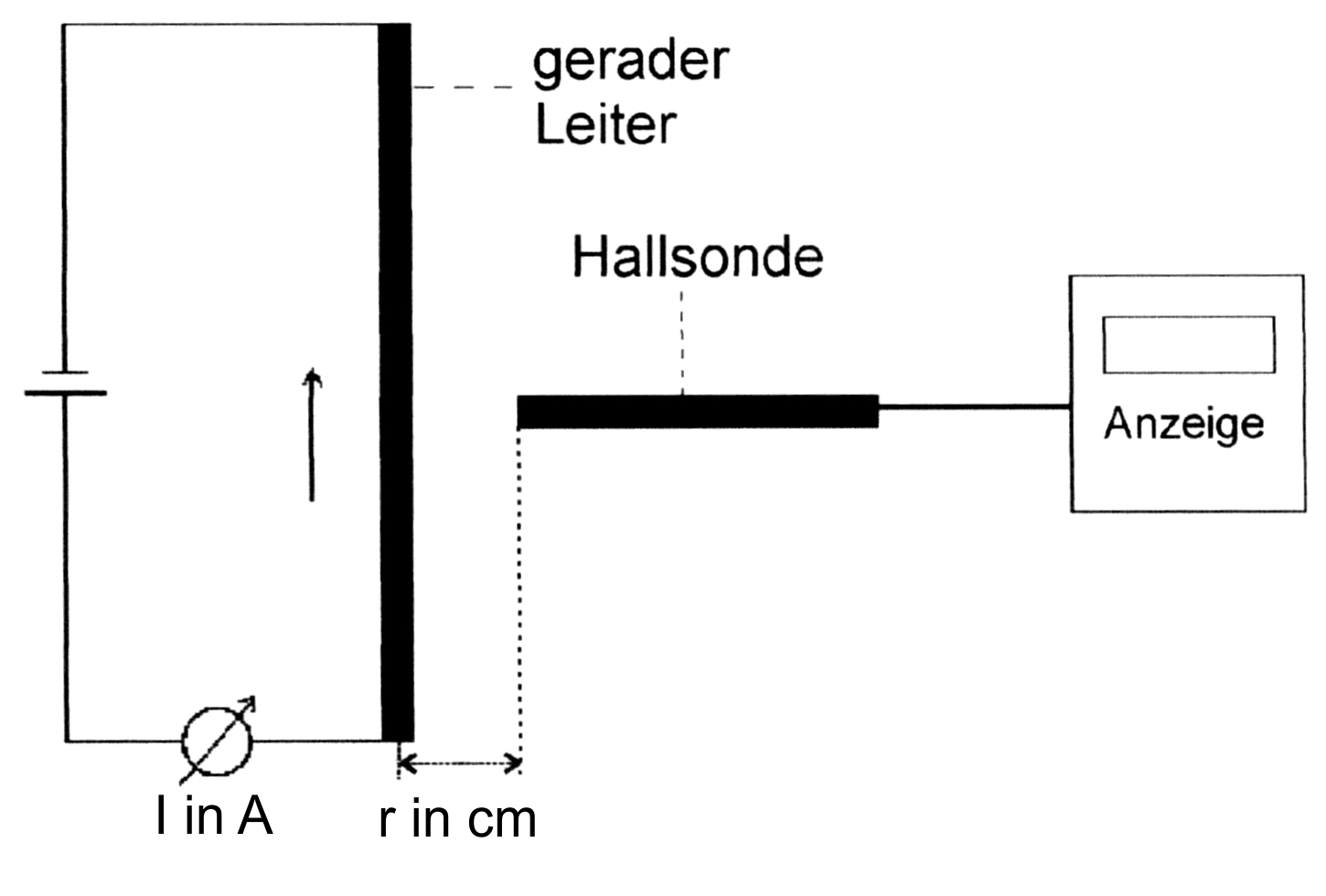
muss möglicherweise (s.u.) hohe Stromstärken liefern können. Schema
eines Versuchsaufbaus mit Hallsonde:
Wenn man
den Versuchsaufbau mit „phyphox“ kennenlernen
möchte, sollte man
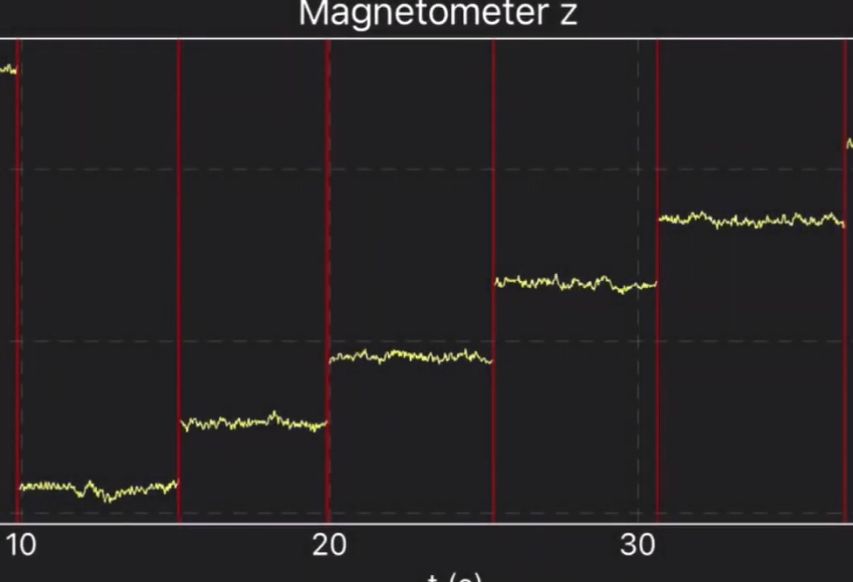
folgenden Videoausschnitt ansehen. Hinweis: Leider wird hier nur die Abhängigkeit von der
Stromstärke gezeigt. Im vollständigen
Video wird auch noch auf die Feldrichtung eingegangen. Mit „phyphox“ sind die Messungen relativ einfach und bei
geringen Stromstärken durchzuführen. Quelle: Ausschnitt aus Videoliste Nr.1 Hinweis: alles Wichtige zur „phyphox“-Messung
unter
folgendem Link 1.
Messung: Die
Hallsonde befindet sich in einem festen Abstand vom Leiter. Die Stromstärke
wird verändert und B gemessen. 2.
Messung: Die
Stromstärke bleibt konstant und der Abstand wird geändert. B wird
wieder gemessen. Versuchsergebnisse: Bei den
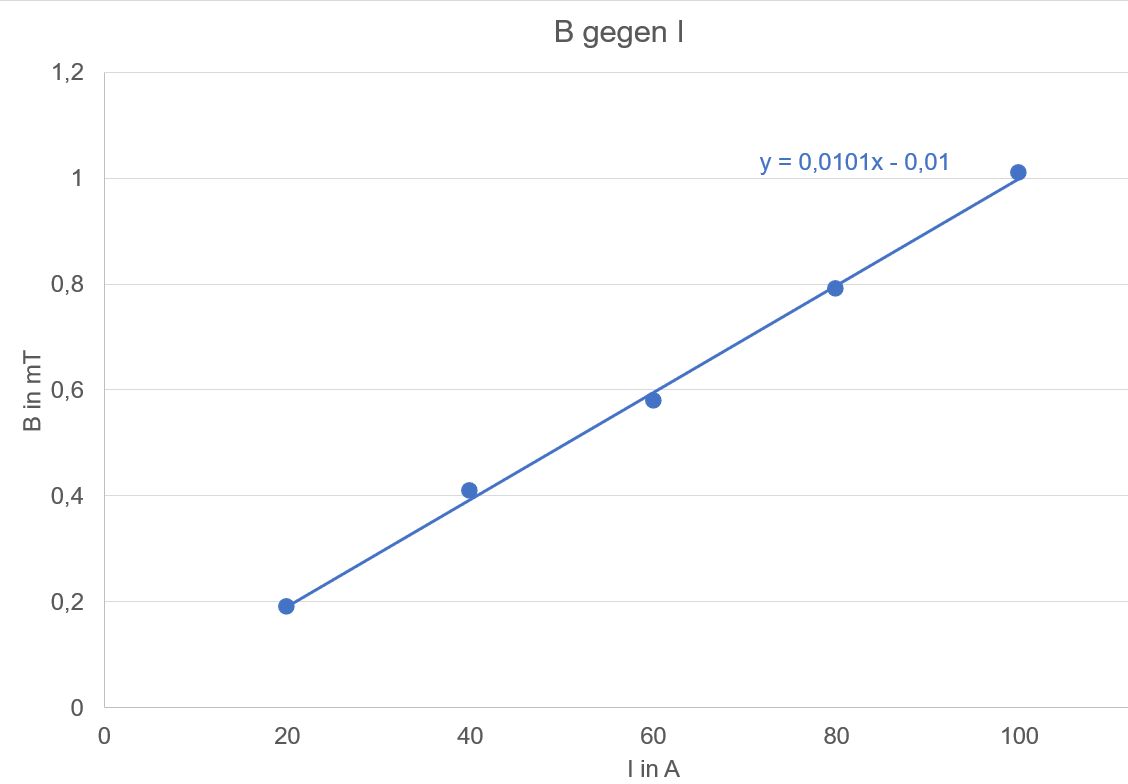
Messungen stellten sich folgende Ergebnisse ein. 1. Messreihe: B in Abhängigkeit von der Stromstärke I ( r = 2 cm = Abstand von der
Mittelachse)
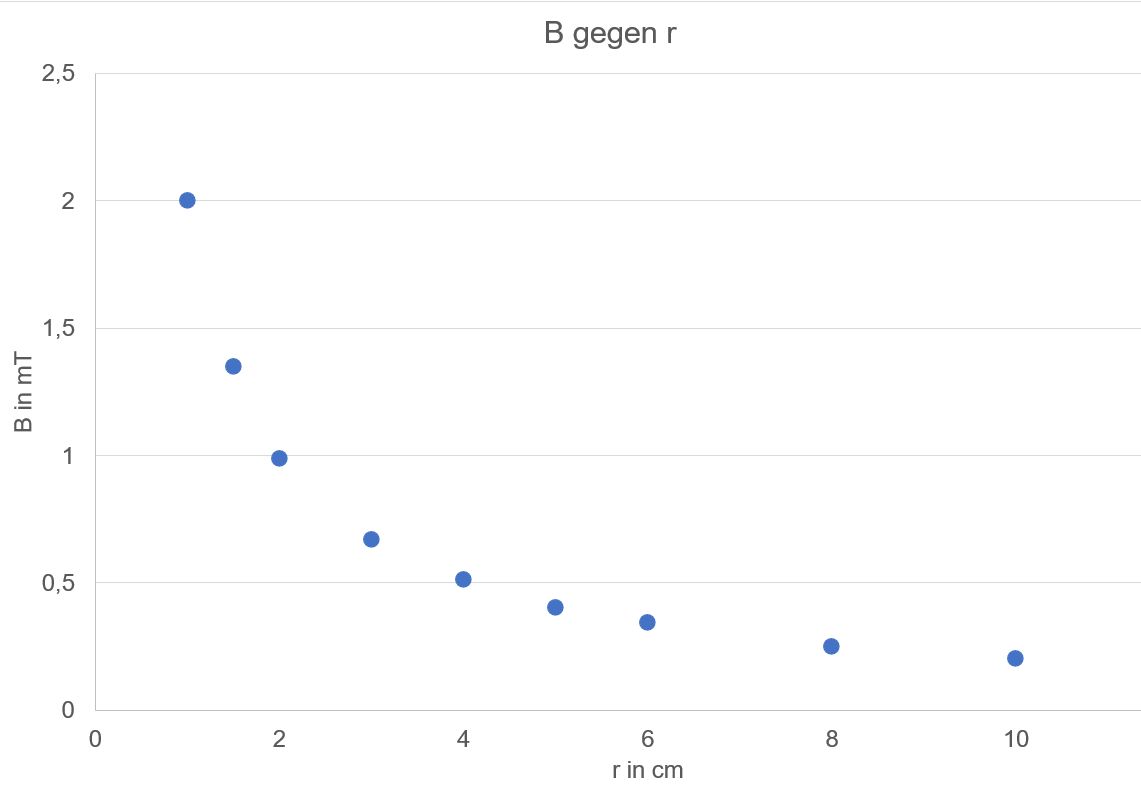
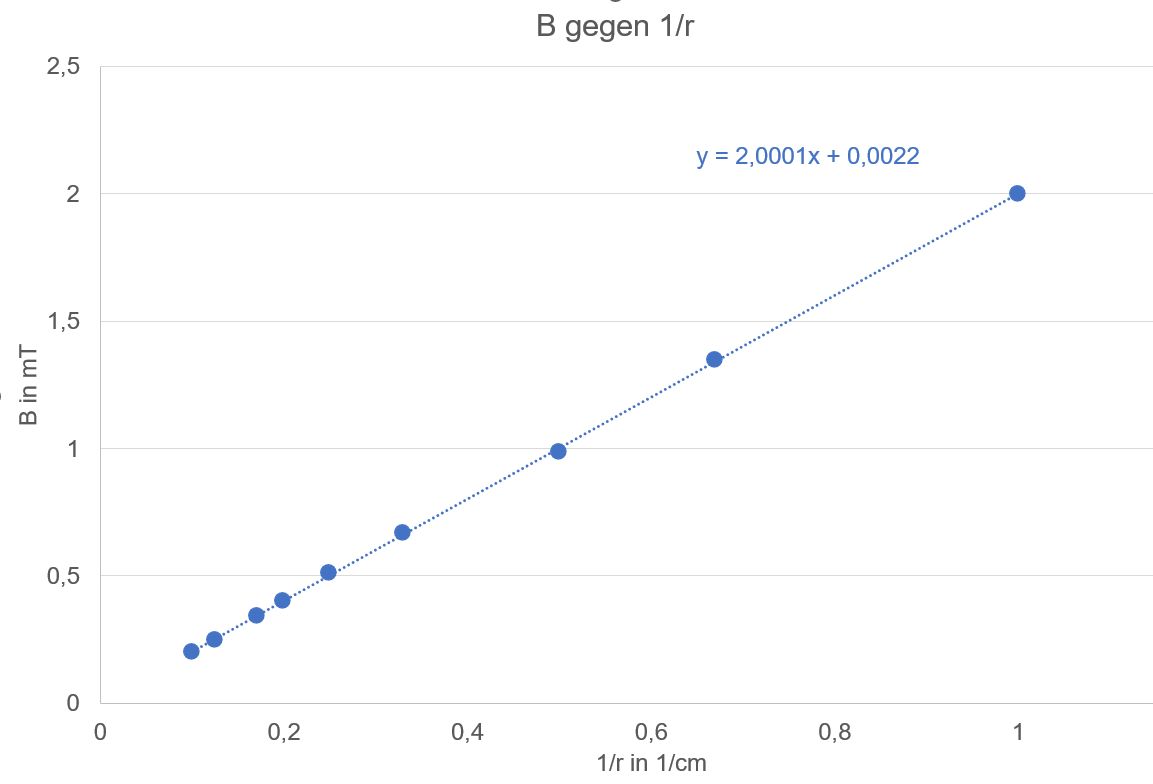
2. Messreihe: B in Abhängigkeit von r ( I =
100 A)
Die
Auswertung erfolgt mit Excel und ergibt:
Auswertung
(Gleichungen, Formeln): Es
ergeben sich folgende Zusammenhänge:
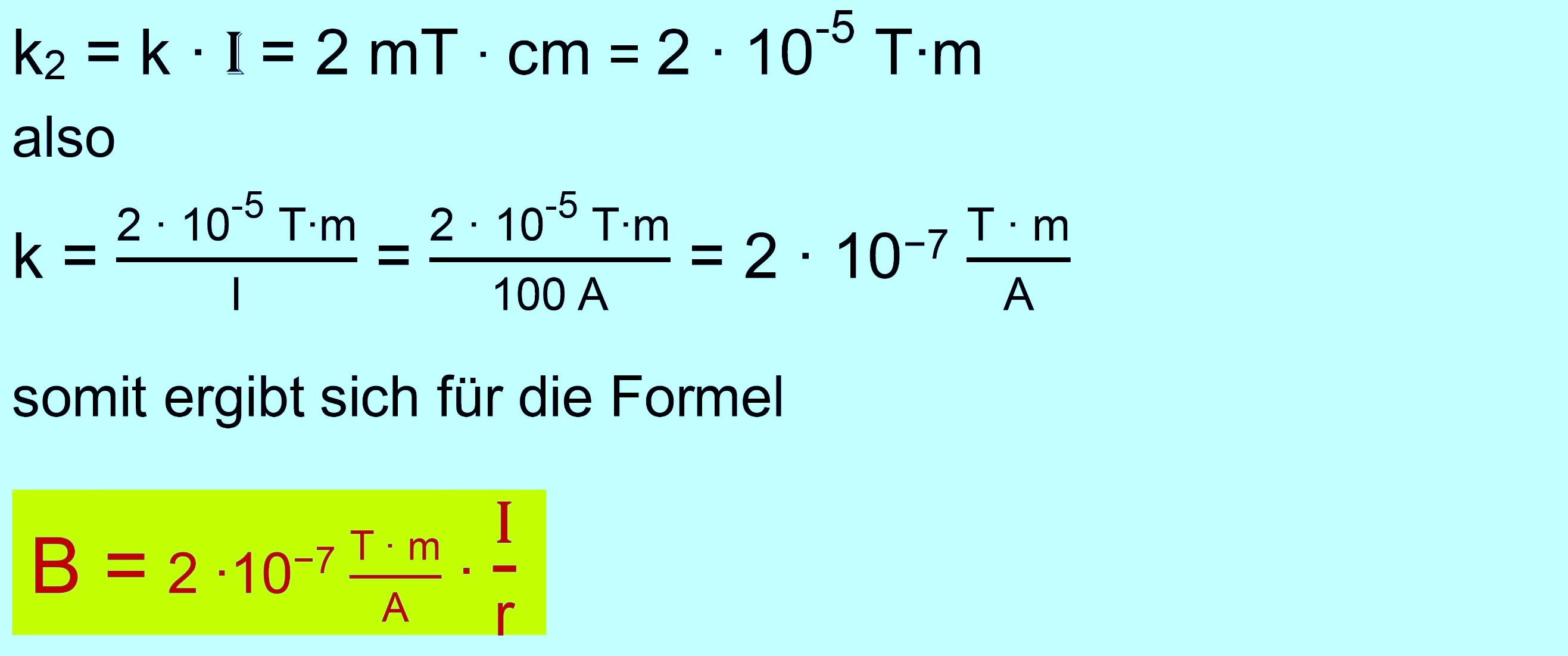
Da die
Formel häufig (s. Rene Matzdorf
- Video 12) aus dem Ampereschen Gesetz (Maxwell-Gleichungen)
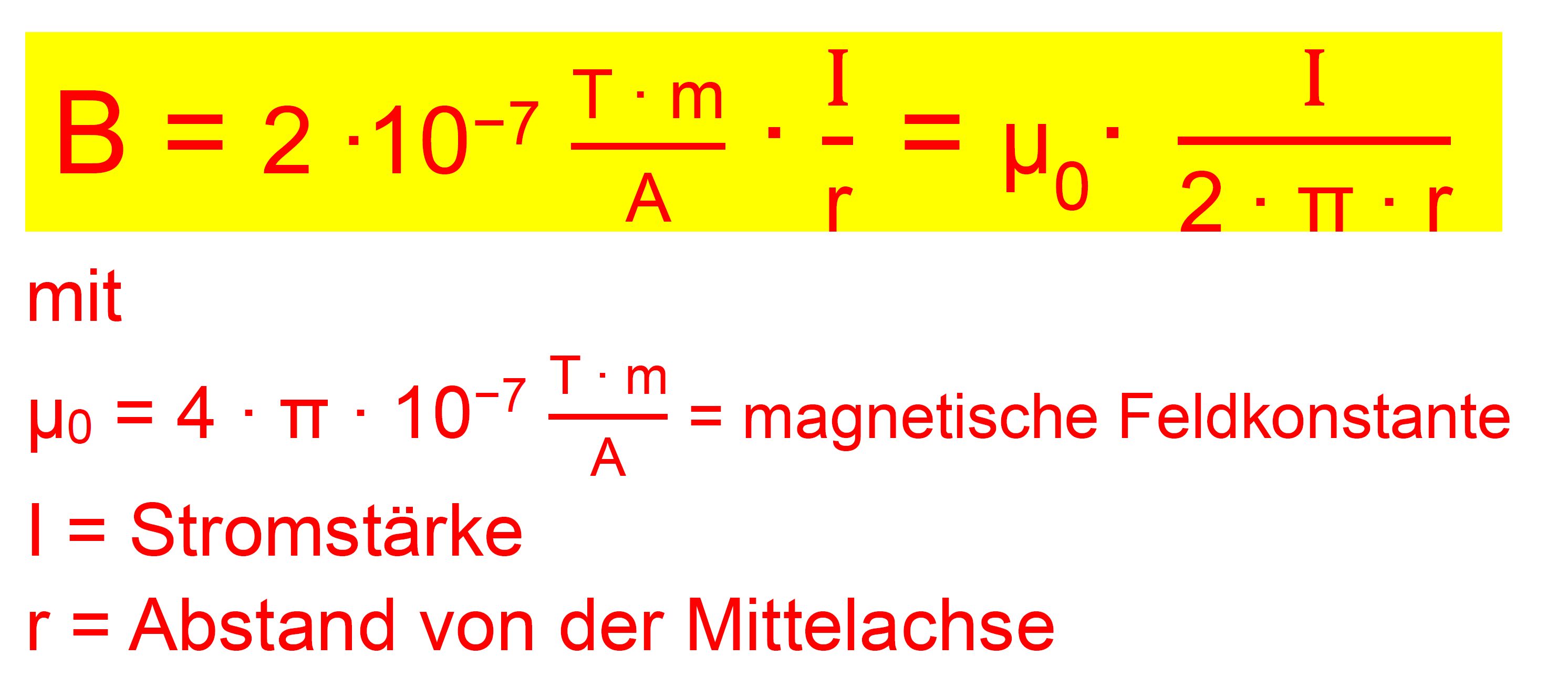
hergeleitet wird, stellt man die Gleichung
noch zu der üblichen Formel mit der magnetischen Feldkonstanten
µ0 um. Es gilt
dann:
Wir
erhalten also schließlich:
Magnetfeld: Kreisring oder
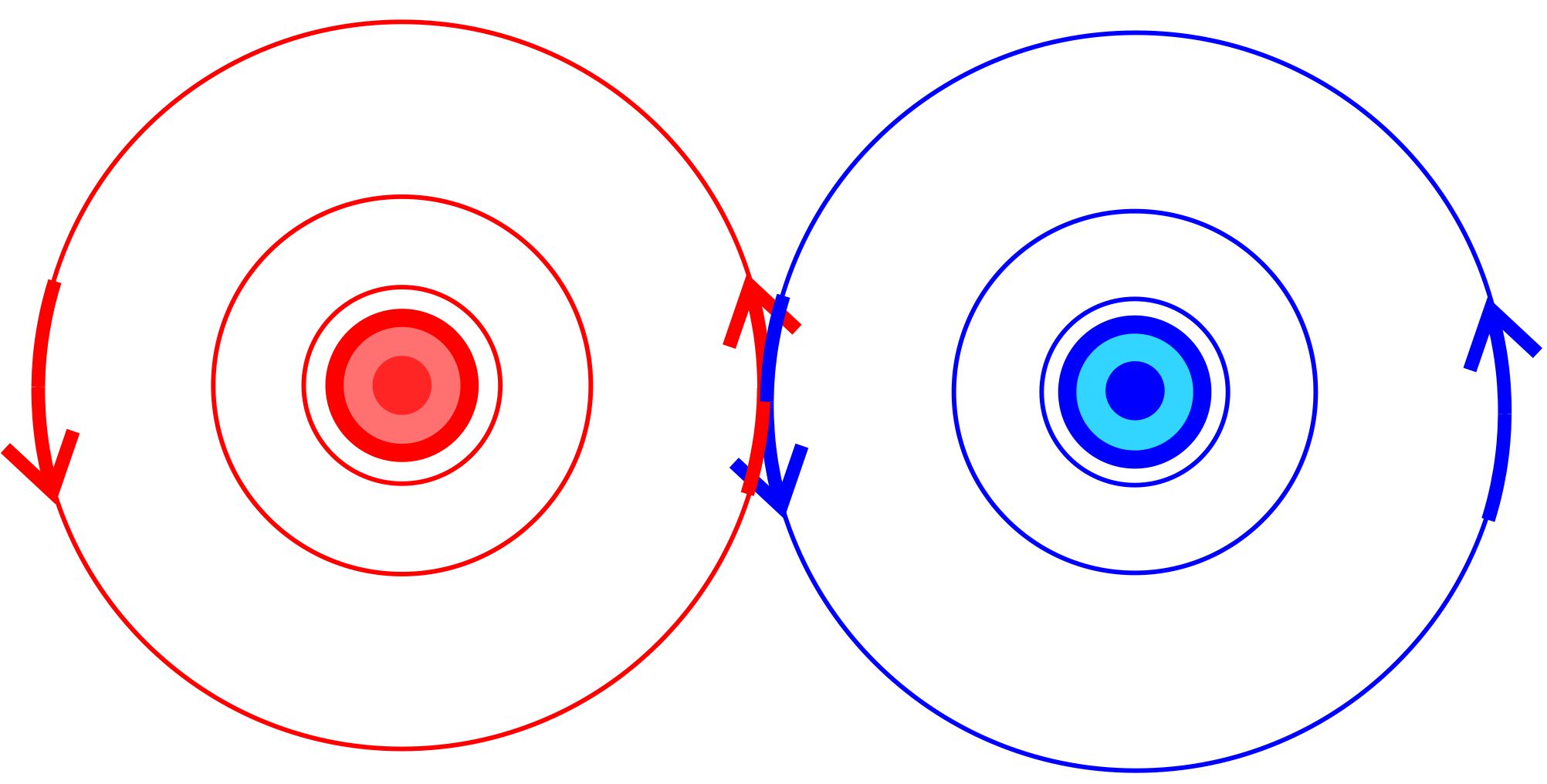
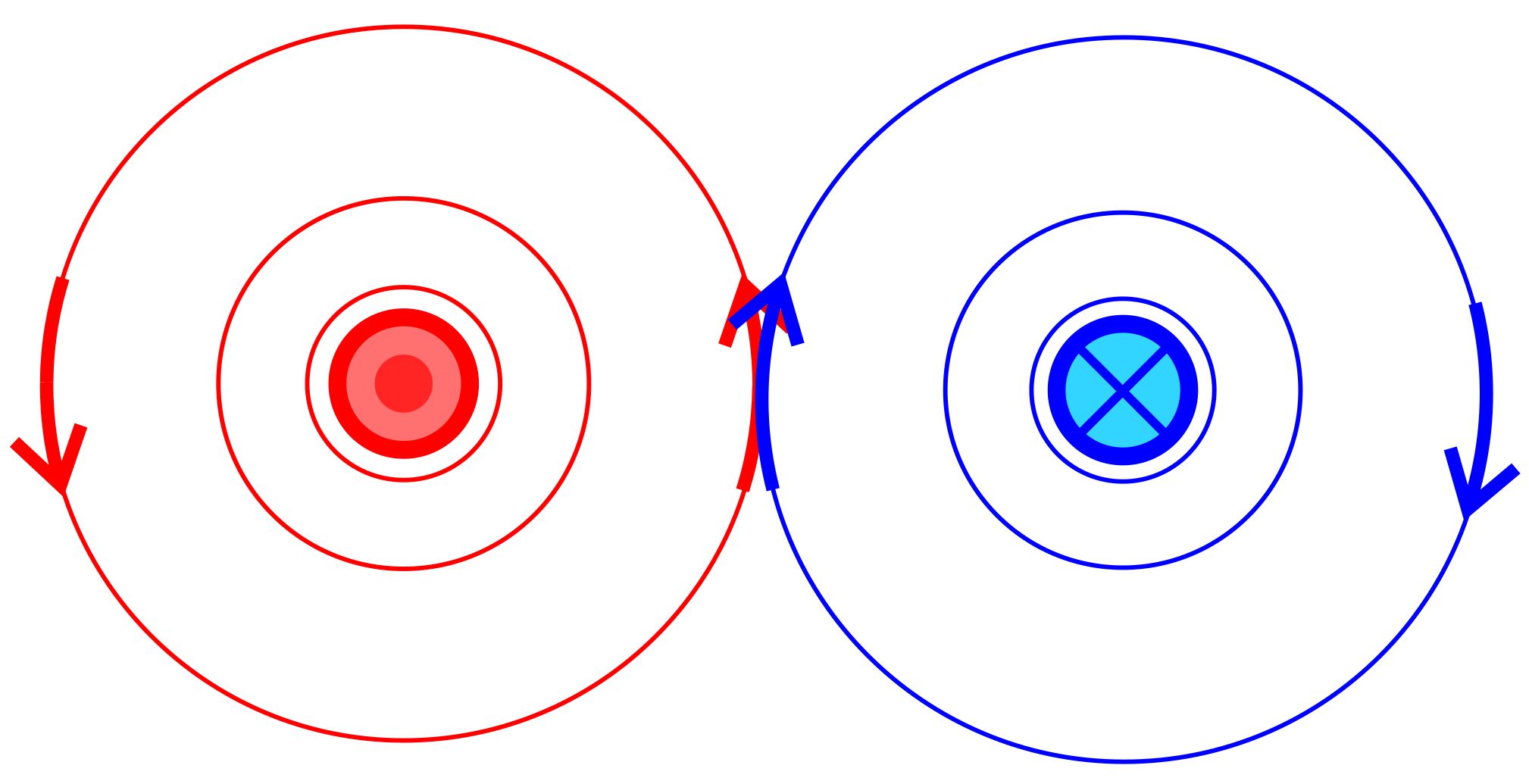
Leiterschleife In diesem Fall wird der gerade Leiter einfach zu einem Kreisring ge-bogen. Das Gesamtmagnetfeld entsteht also aus der Überlagerung des Magnetfeldes gerader Leiter. Es stehen sich praktisch im Ring immer zwei gerade Leiterteile gegenüber, durch die der Strom in ent- gegengesetzter Richtung fließt. In diesem Fall verstärken sich die Magnetfelder. Das Magnetfeld im Ring ist also verstärkt. Außerhalb wird das
Feld abgeschwächt, da dort die Magnetfelder gegeneinan-der
gerichtet sind (s. Abb.).
Die
folgenden Abbildungen zeigen das Magnetfeld (Eisenfeilspäne, Magnetnadeln).
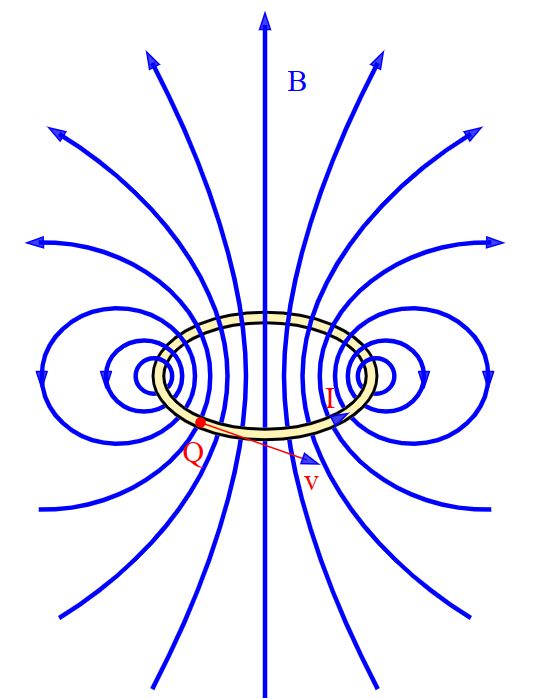
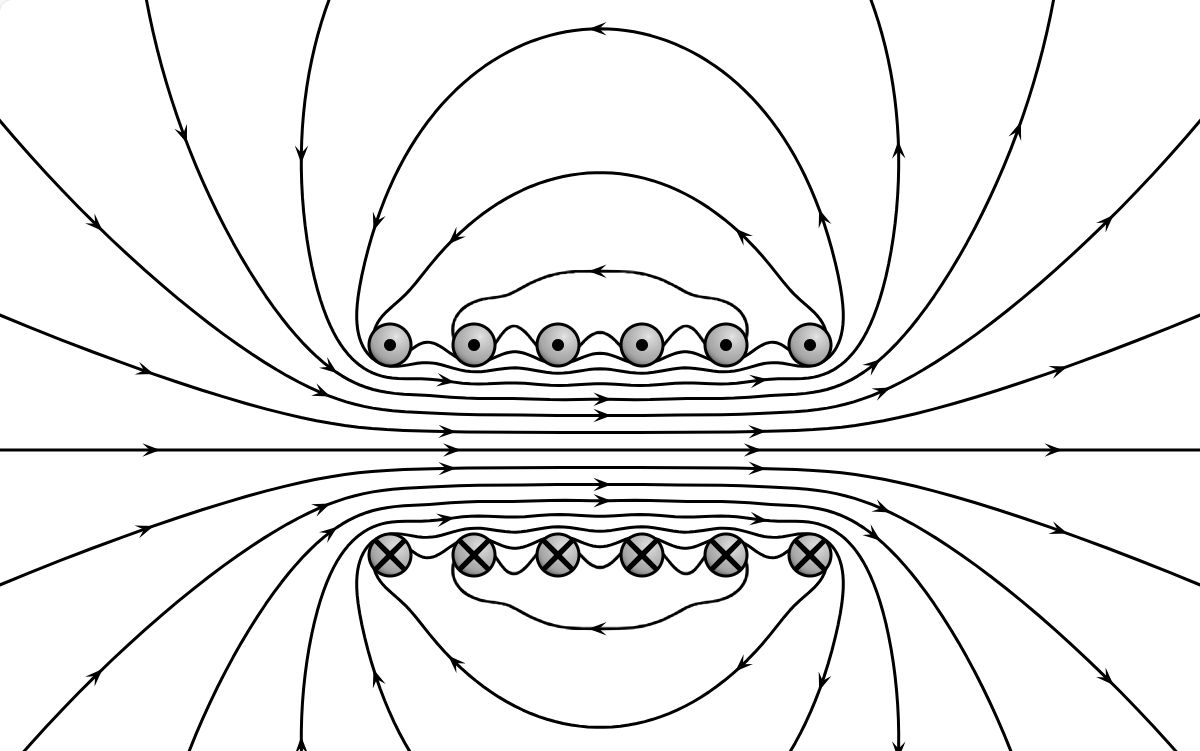
Schematisch
sähe das Feld dann so aus:
Quelle: wikipedia Da das
Magnetfeld einer Leiterschleife im Physik-Unterricht der Oberstufe
keine Rolle spielt, gibt es hierzu keine Messreihen, die man auswerten
könnte. In der einschlägigen Literatur (hier insbesondere „Tipler“) werden theoretische Herleitungen aus dem Biot-Savartschen-Gesetz
gemacht. Diese findet man auch bei wikipedia. Ich gebe
hier nur das Ergebnis für eine große Entfernung von der Leiterschleife
(z>>r) auf der Symmetrieachse an. Dann ergibt sich
Bei einer
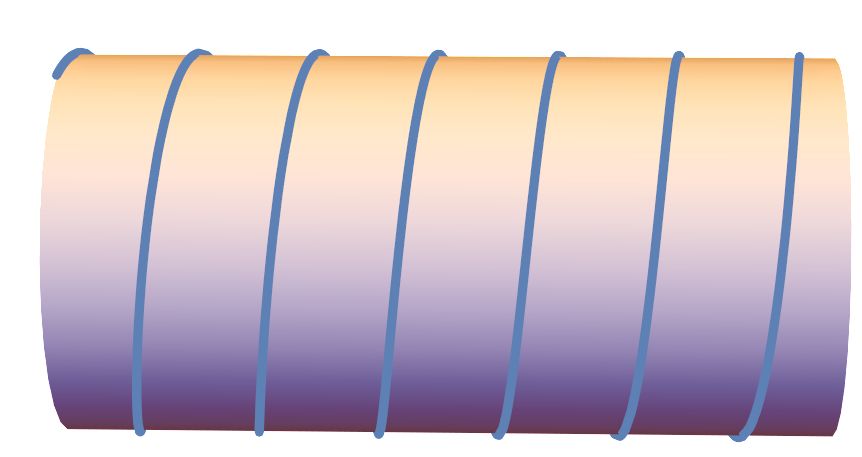
Spule werden mehrere Leiterschleifen nacheinander auf- gebaut.
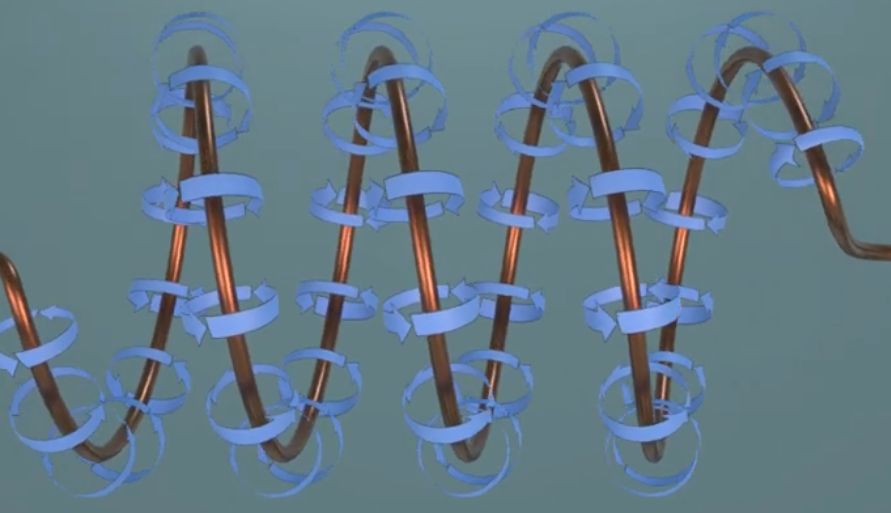
Ein leitender Draht wird also spiralförmig auf einem „Zylinder“ aufgewickelt.
Das sieht also in etwa wie folgt aus:
Hinweis: Es muss nicht immer genau eine kreisförmige
Querschnittsfläche vorliegen. Häufig sind die Querschnittsflächen eher quadratisch oder
rechteckig. Alle Lehrmittelfirmen
bieten Spulen mit vielen verschiedenen Win- dungszahlen
an. Dies kann man gut für die Messungen (s.u.) aus- nutzen,
da praktisch jede Schule in der Physiksammlung ein großes Sortiment
solcher Spulen vorweist. Das
Magnetfeld lässt sich aufgrund des Aufbaus also als Überlager- ung des
Magnetfeldes vieler Leiterschleifen verstehen. Dies bedeutet sofort, dass das
Magnetfeld im Inneren der Spule aufgrund dieser ver- stärkenden
Überlagerung sehr groß und recht homogen sein sollte. Da
wiederum das Magnetfeld einer Leiterschleife mit dem Magnetfeld gerader
Leiter zusammenhängt (s. Magnetfeld Leiterschleife), lässt sich das
Magnetfeld einer Spule letztendlich auf das Magnetfeld eines langen
Leiters zurückführen. Folgende
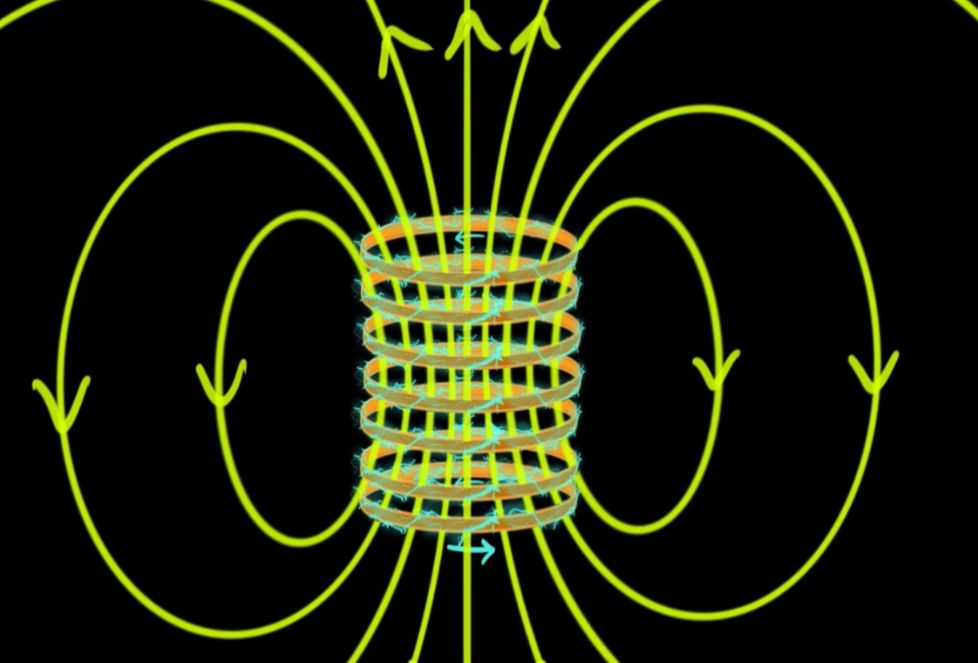
Simulationen zeigen dies noch einmal:
Wir
haben dann insgesamt folgendes Aussehen:
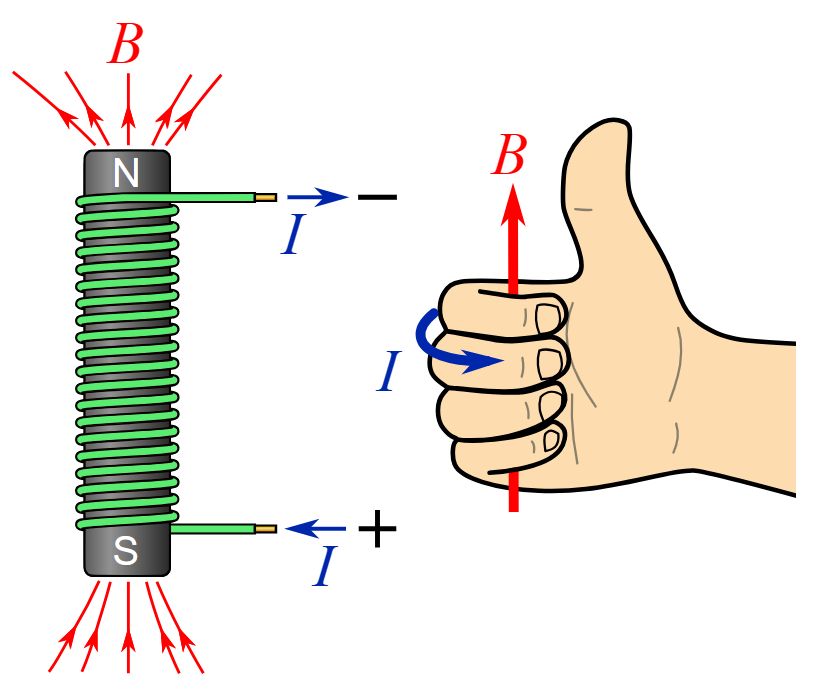
Für
die Richtung des Magnetfeldes im Inneren der Spule gilt übrigens die
Rechte-Faust-Regel.
Quelle für die Abbildung: wikipedia Hinweis: Es ist manchmal nicht einfach die technische
Stromrichtung herauszufinden. Bitte genau auf die Wicklungsrichtung achten! Wenn man
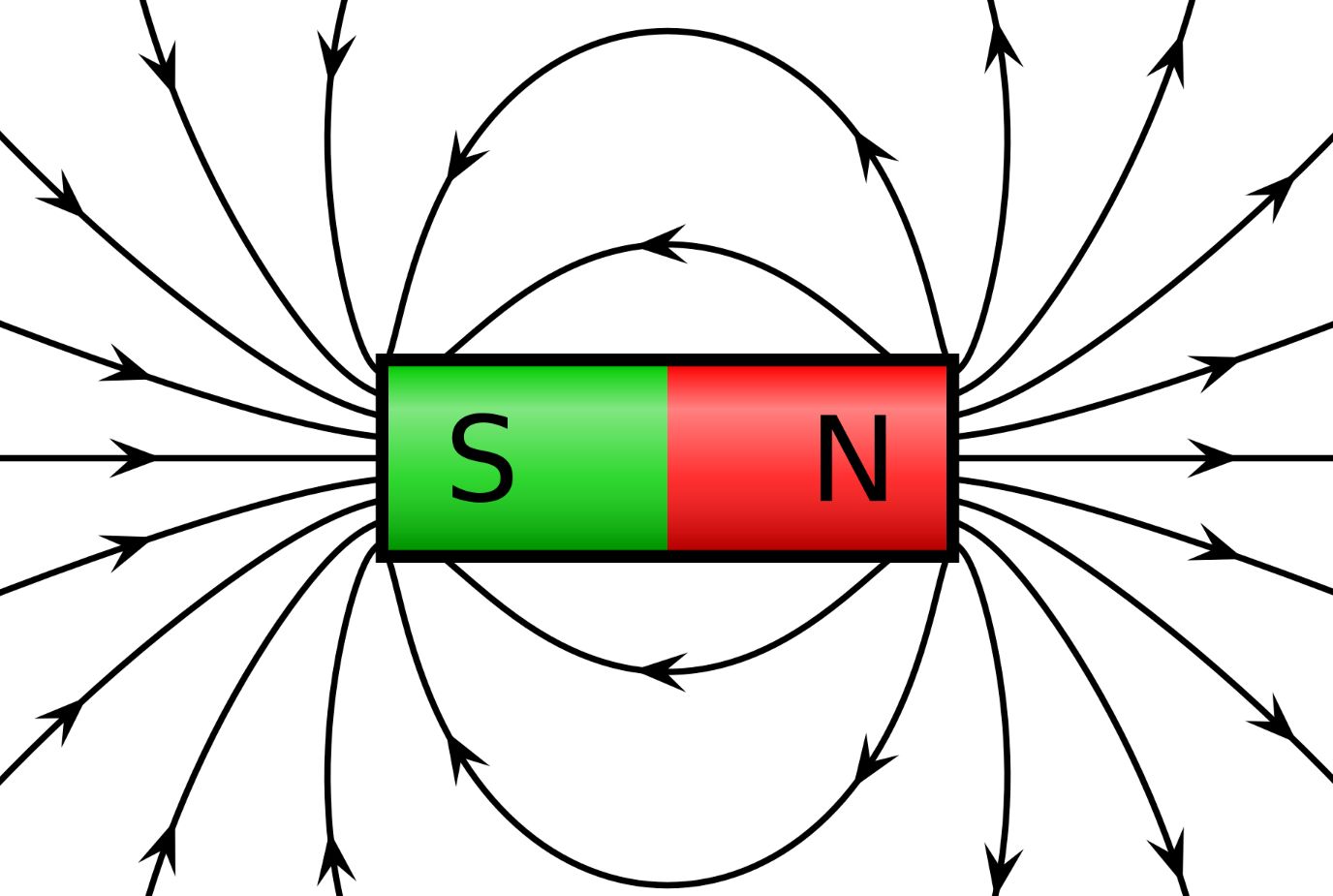
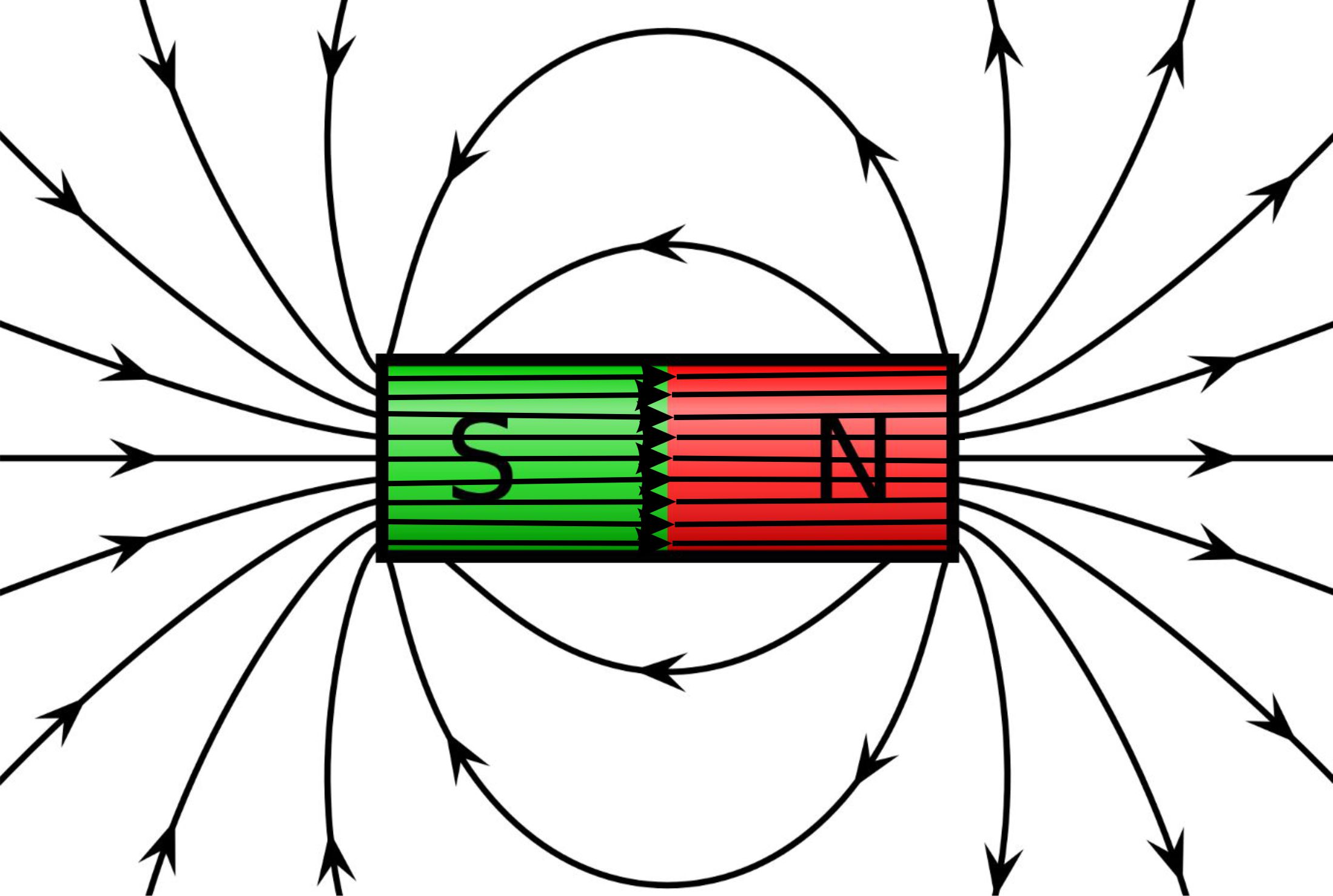
einmal die Magnetfelder von Spule und Stabmagnet ver- gleicht,
sieht man, dass diese sehr ähnlich aussehen.
Quelle: Spule-wikipedia; Stabmagnet-wikipedia Der
Vergleich führt natürlich sofort dazu, dass man annehmen kann, dass das
Magnetfeld des Stabmagneten sich innerhalb des Stab- magneten
fortsetzt, so dass man auch ein Feld innerhalb des Stab- magneten
hat, welches dem der Spule ähnelt. Das sähe
dann so aus:
Dies
würde bedeuten, dass wir auch hier geschlossene
Feldlinien vor- liegen
haben. Alle bisherigen Magnetfelder durch Stromfluss sind ebenfalls
geschlossen. Sie stammen ja alle vom Magnetfeld des geraden Leiters ab. Dies ist
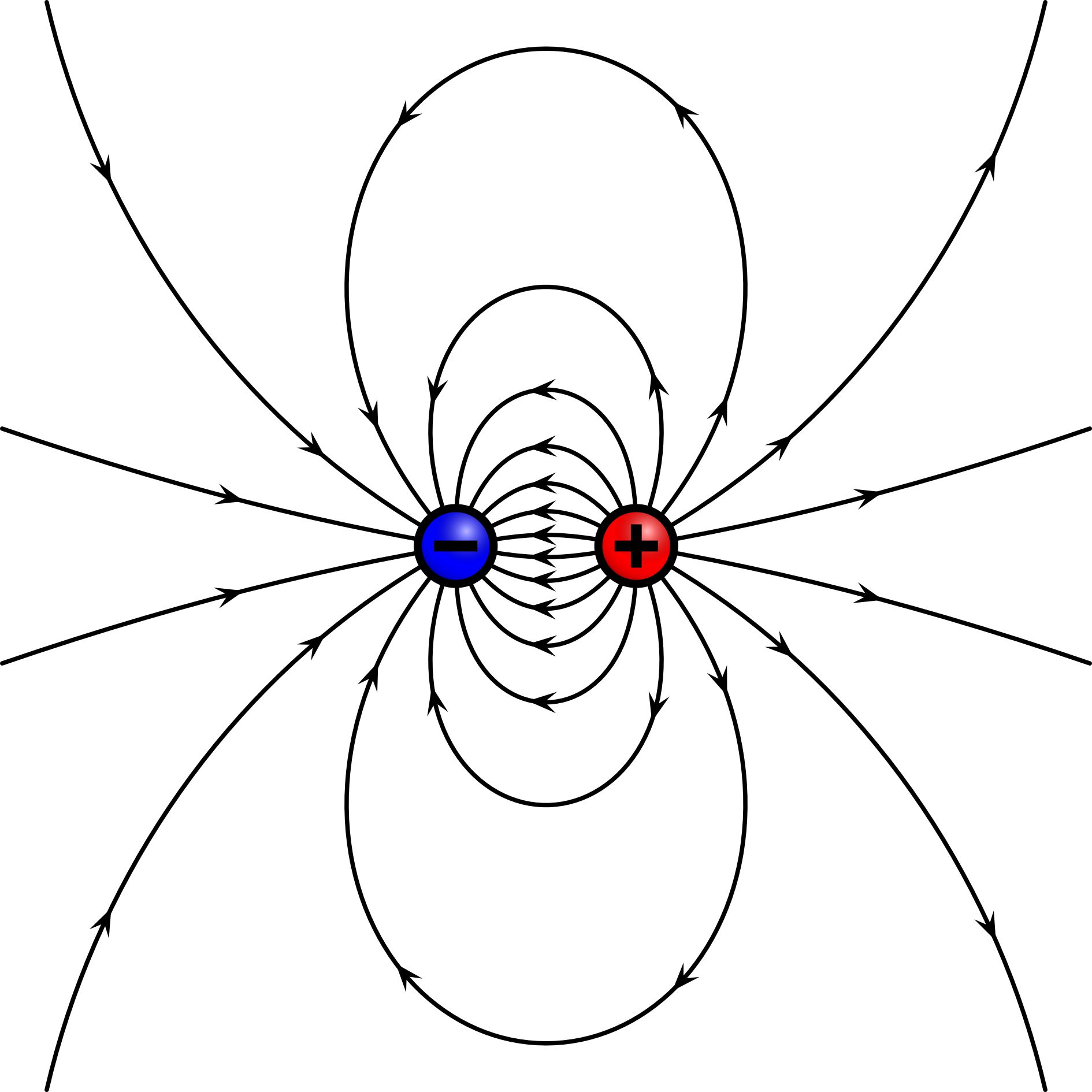
der grundlegende Unterschied zwischen dem elektrischen und
magnetischem Feld. Im elektrischen Feld gibt es Quellen (Start- punkte) des
Feldes, nämlich die positiven Ladungen, und Senken (Zielpunkte),
nämlich die negativen Ladungen. Im elektrischen Feld starten
die Feldlinien immer bei positiven Ladungen und enden auf negativen
Ladungen. So etwas wird Quellenfeld genannt. Im Magnetfeld gibt
es nur geschlossene Feldlinien. Man spricht von einem Wirbelfeld. Noch
einmal zum Vergleich: Es
werden verschiedene Zusammenhänge untersucht, und zwar die Abhängigkeit
zwischen B und 1.) der
Stromstärke 2.) der
Anzahl der Windungen 3.)
Länge der Spule 4.) Querschnittsfläche
Für mich
war es am einfachsten die drei ersten Abhängigkeiten an- hand
vieler Einzelspulen zu untersuchen, die von praktisch allen Lehrmittelfirmen
zur Verfügung gestellt werden. Ich konnte aus folgen- dem
Angebot der Firma Phywe auswählen:
Meine
Entscheidung fiel auf: −
eine Spule mit n = 1200 Windungen −
zwei Spulen mit n = 600 Windungen −
vier Spulen mit n = 300 Windungen −
eine Spule mit n = 900 Windungen Man muss
nur die entsprechende Auswahl treffen, um alle drei Ab- hängigkeiten
zu untersuchen. 1.)
Abhängigkeit von I: I verändern, B messen; l = 6,8 cm
und n = 1200 Windungen bleiben konstant Gemessen
wurde mit einer Hallsonde. Der Versuchsaufbau hatte folgendes
Aussehen.
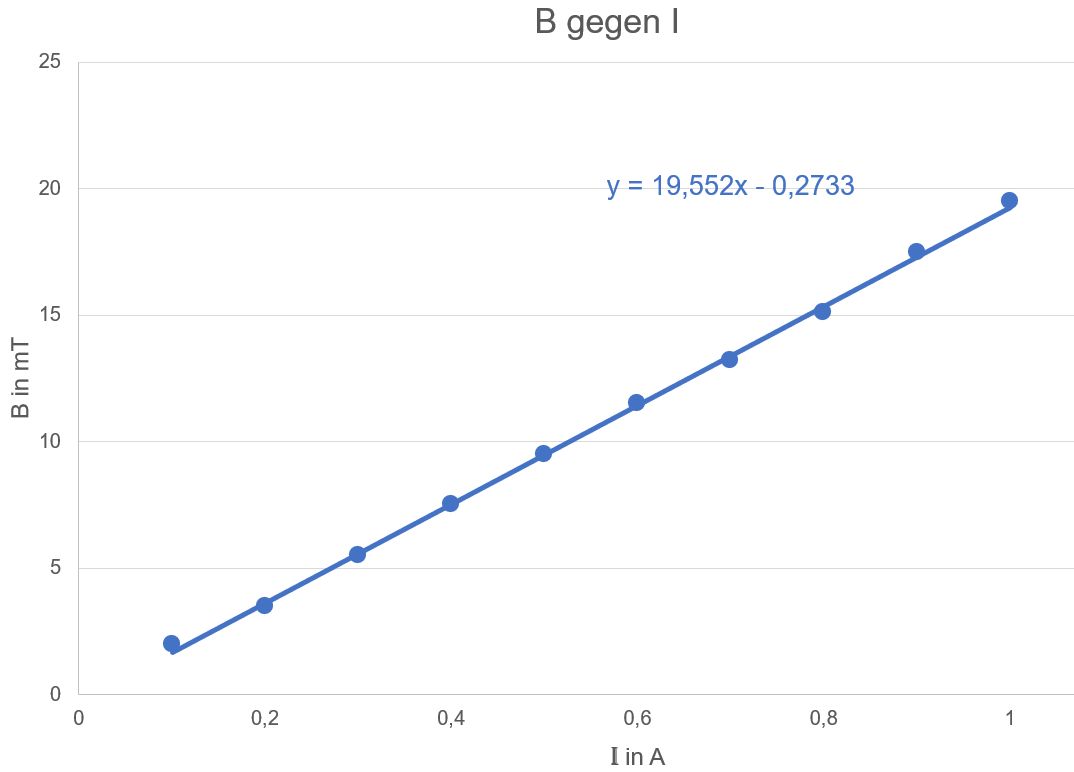
Messwerte:
Auswertung:
Ergebnis:
Man erhält eine Ursprungsgerade, also B proportional zu I 2.)
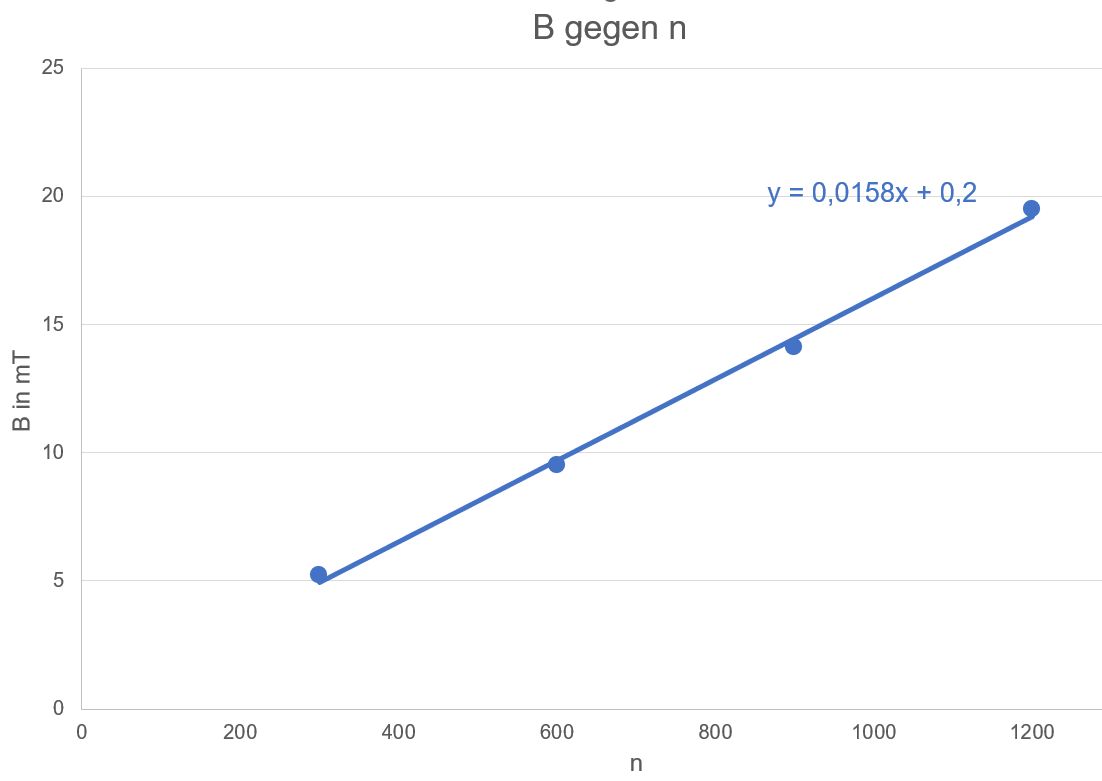
Abhängigkeit von n: n verändern, B
messen l = 6,8
cm und I = 1 A
konstant alle Spulen
haben die Länge 6,8 cm, man wählt jetzt einfach vier Spulen
mit unterschiedlicher Windungszahl und misst B bei jeweils einer
Stromstärke von 1 A Messwerte:
Auswertung:
Es liegt
eine Ursprungsgerade vor, also ist B proportional zu n. 3.)
Abhängigkeit von l: l verändern, B
messen n = 1200
und I = 1 A
konstant Wir müssen
uns hier etwas einfallen lassen, da es keine Einzelspulen mit
unterschiedlicher Länge gibt. Alle haben eine Länge von 6,8 cm. Man
schaltet jetzt verschiedene Spulen hintereinander, so dass jeweils eine
Windungszahl von 1200 vorliegt: eine
Spule mit n=1200 → l = 6,8 cm zwei
Spulen mit n=600 → l = 13,6 cm vier
Spulen mit n=300 → l = 27,2 cm Die
Messungen müssen exakt innerhalb einer der Spulen stattfinden. Messwerte:
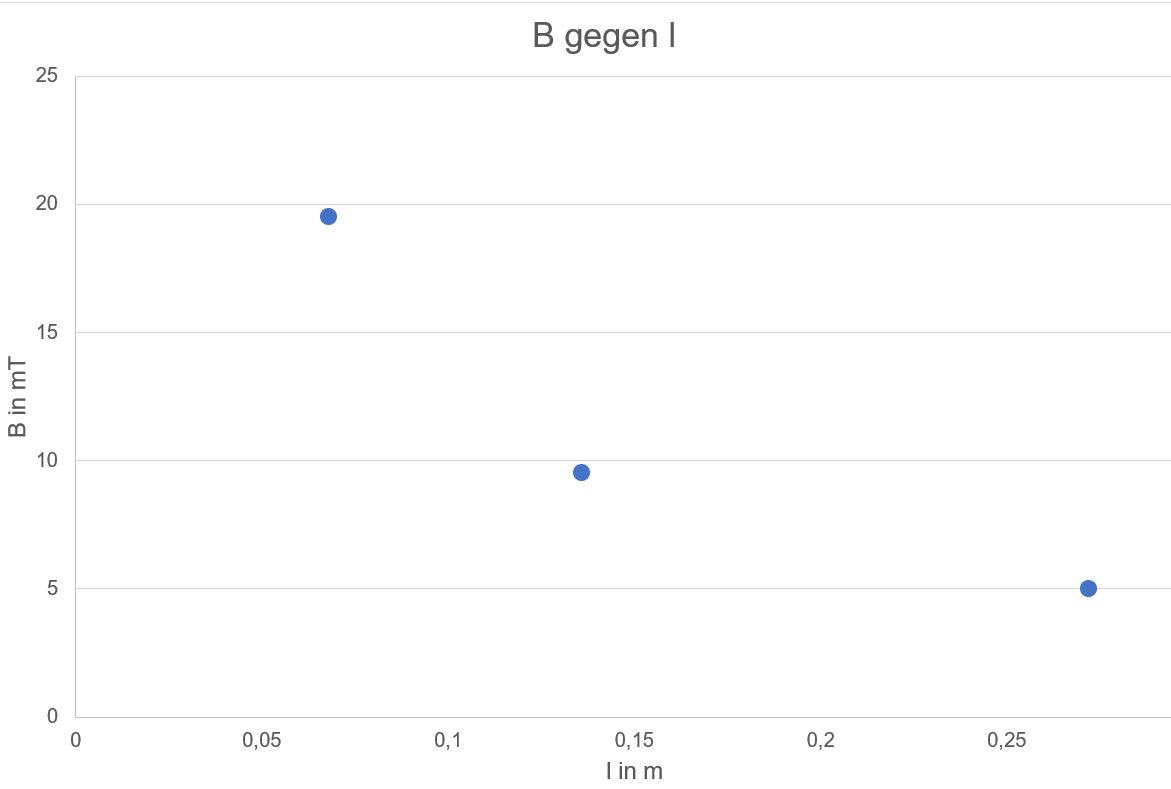
Auswertung:
Keine
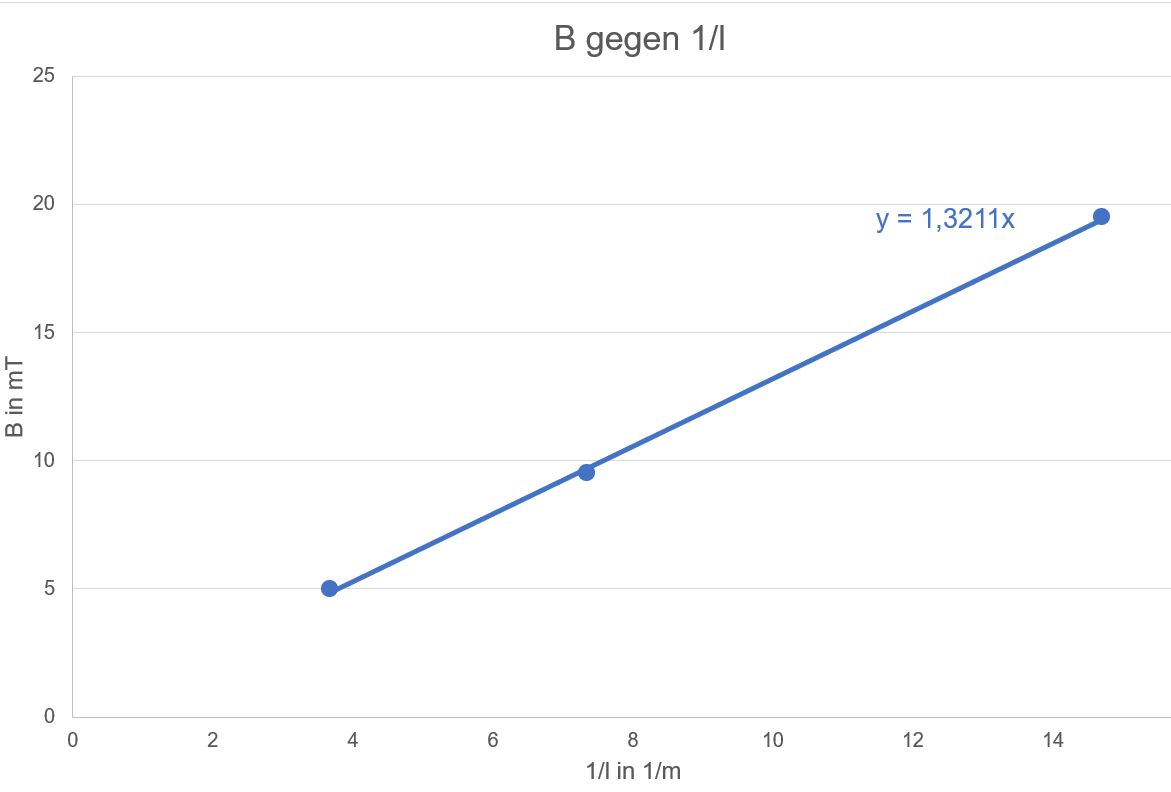
Ursprungsgerade, sondern eher Hyperbel → Neuer Auftrag
Ursprungsgerade
liegt vor, also ist B proportional zu 1/l 4.)
Abhängigkeit von der Querschnittsfläche: Diese
Abhängigkeit ist leider nicht mit dem obigen Sortiment an Spulen
zu untersuchen. Auf dem
Videoportal „physik mit c“ wird hier allerdings
eine Messung an zwei
Zylinderspulen durchgeführt. Das folgende Video zeigt den Versuchsablauf: Quelle: Ausschnitt aus Liste Nr. 8 Es besteht
keine Abhängigkeit von der Querschnittsfläche bzw. vom Radius
der Spulen. Auswertung
(Gleichungen, Formeln): Es
ergeben sich folgende Zusammenhänge:
Hinweis: Diese Formel gilt
tatsächlich nur im Inneren einer langen Spule. Theoretische Berechnungen mit dem Biot-Savartschen-Gesetz zeigen, dass
am Rand oder bei kurzen Spulen auch der Radius und der
Abstand vom Mittelpunkt berücksichtigt werden müssen (s. ein- schlägige
Literatur z.B. Tipler) Wird die
Spule noch in ihrem Inneren mit einem magnetisierbarem Material,
meist Weicheisen,
versehen, steigert sich die Feldstärke um ein
Vielfaches. Dieses Vielfache wird durch eine Materialkonstante µr
= relative Permeabilität berücksichtigt. Die Formel lautet dann:
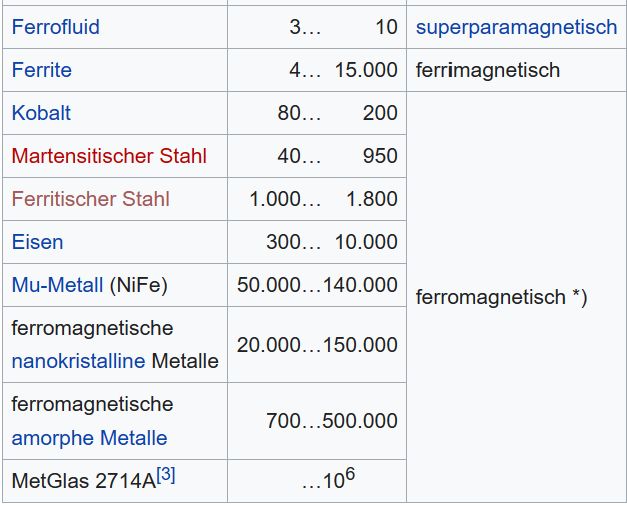
Zu den
möglichen Werten für µr ein Ausschnitt aus einer Tabelle von wikipedia:
Quelle: wikipedia zum Abschnitt:
zum vorherigen Kapitel: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||