|
zum Abschnitt:
Hall-Effekt Der
Hall-Effekt ist nach seinem Entdecker Edwin H. Hall benannt,
der ihn 1879
im Rahmen seiner Doktorarbeit gefunden hat. Er fand
heraus, dass, wenn man eine stromdurchflossene Leiterplatte in ein
Magnetfeld gibt, an den Seiten der Platte Spannungen auftreten. Dieser
Effekt hat in vielen Sensoren Anwendung gefunden. In der Schule dient
er vor allem dazu, die Stärke von Magnetfeldern zu mes- sen. Man spricht dann von einer Hallsonde. Hall-Effekt −
Aufbau Der
Aufbau ist eigentlich recht einfach. Das größte Problem in der Schule
ist eher, die Messung der sehr geringen Spannung durchzu- führen. Man
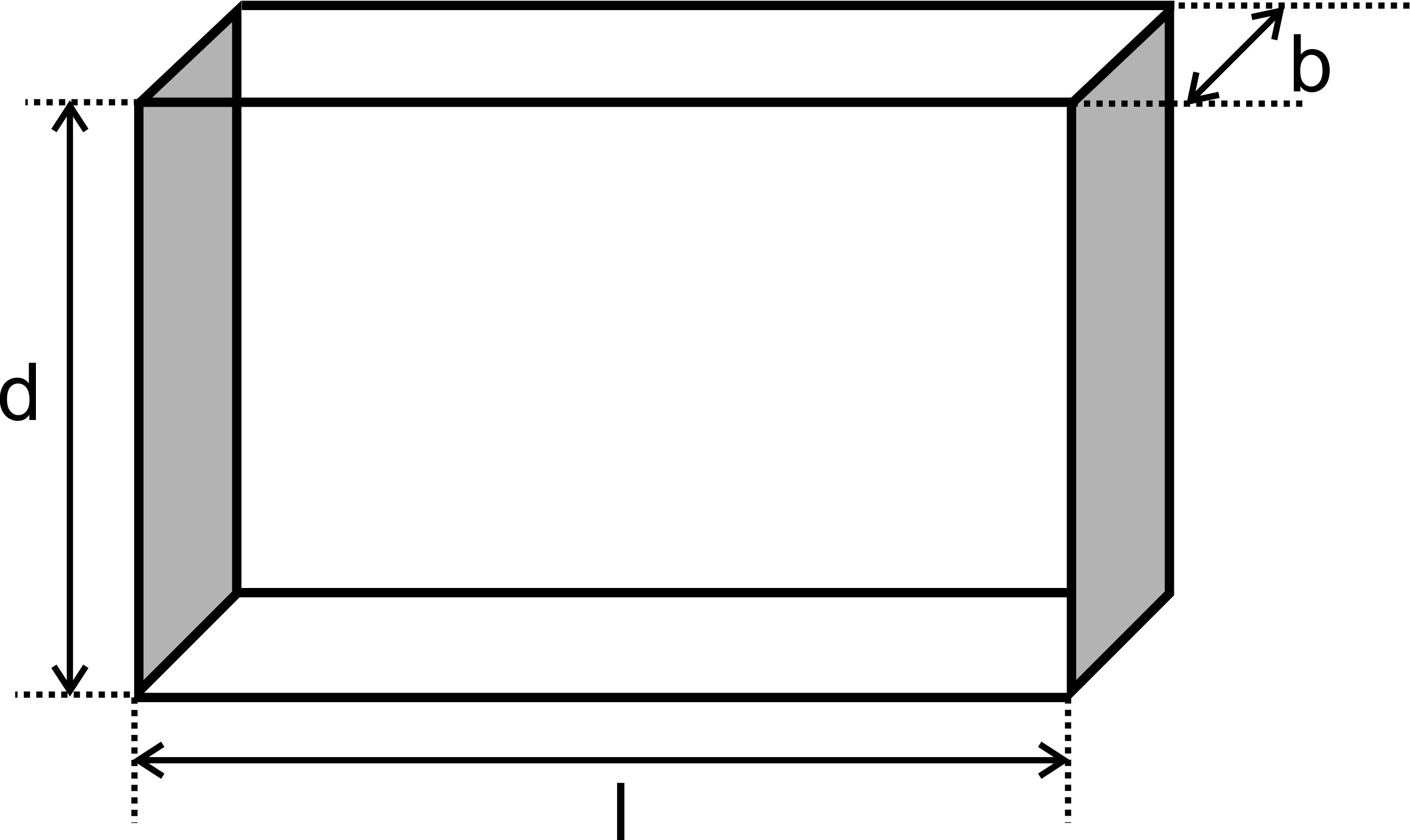
braucht eine stromdurchflossene Leiterplatte (oder schmalen Quader)
aus nicht magnetischem Material, meist wird eine Silberplatte gewählt.
Den größten Effekt erzielt man allerdings, wenn man einen Quader
aus Bismut (Wismut) wählt. Diese Platte wird so in ein Ma- gnetfeld
gegeben, dass die Feldlinien senkrecht zur Stromrichtung stehen. Hierzu
eine schematische Abbildung:
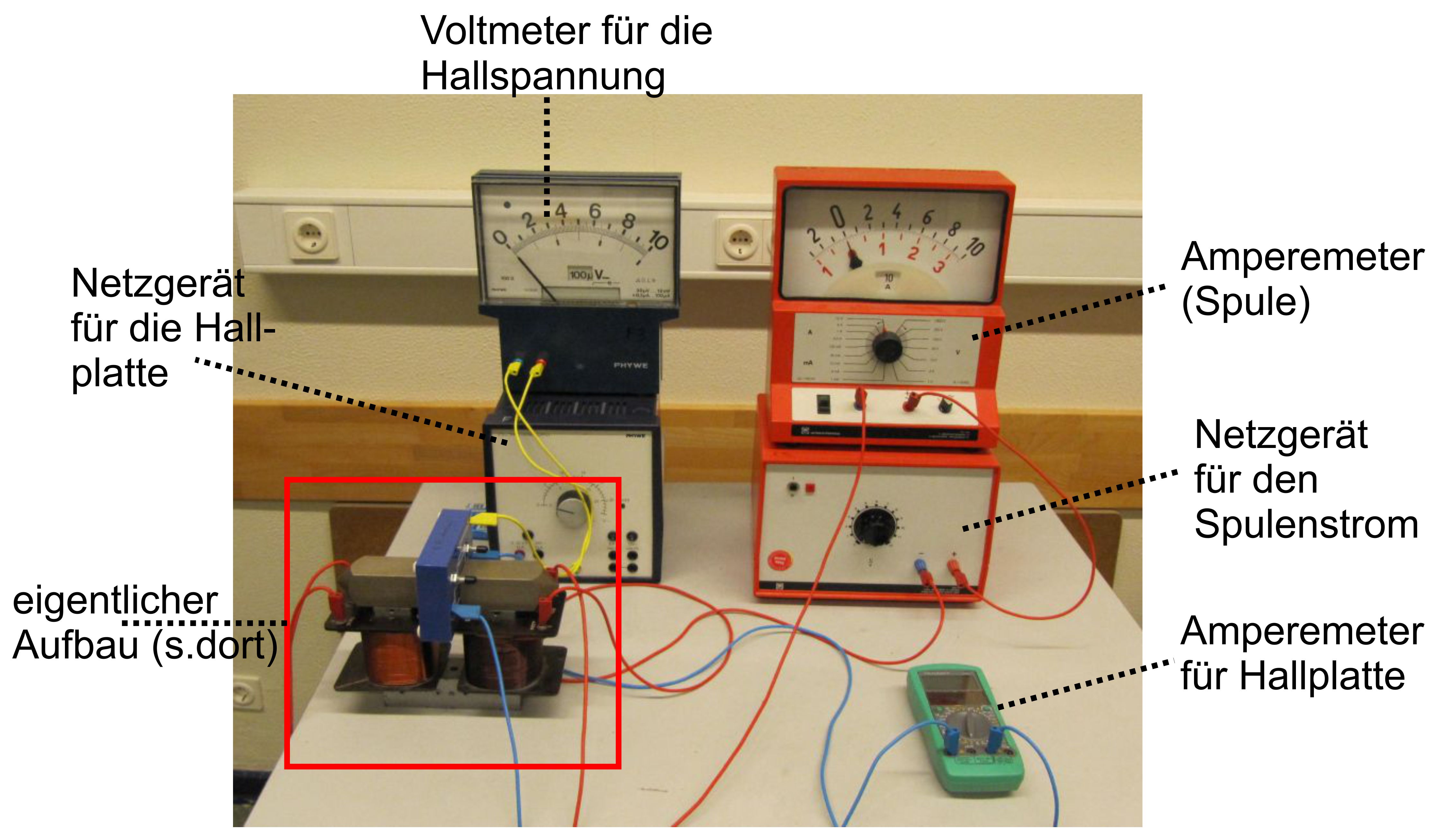
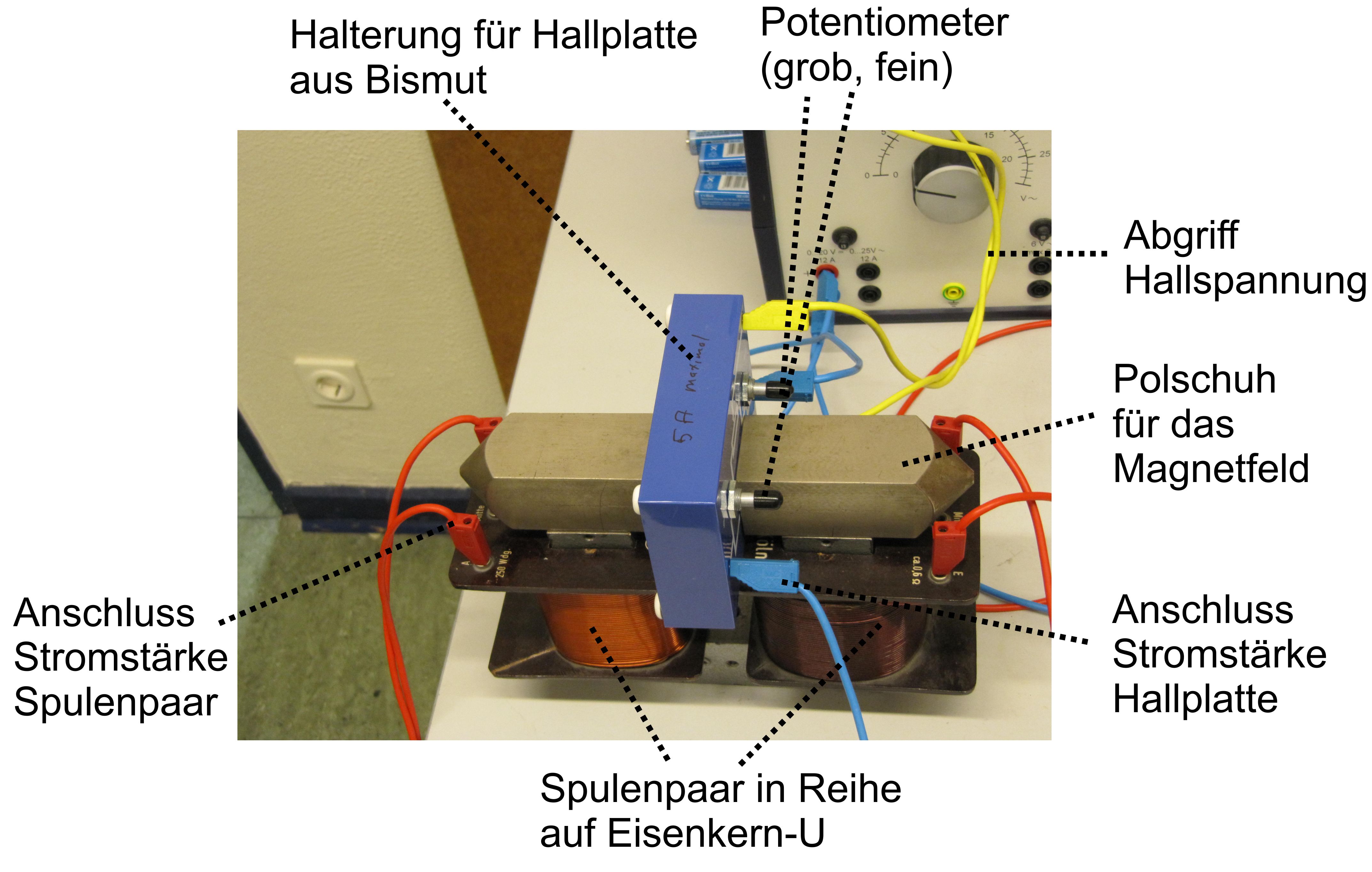
Im Folgenden sieht man den Versuchsaufbau, den ich
in der Schule benutzt
habe; einmal die Gesamtübersicht und dann den eigentlichen Hall-Aufbau
im Detail.
Übersicht
Detail Hinweis: wer an dem Aufbau mit der Silberplatte
interessiert ist, sollte sich die PDF von Leybold ansehen
(Link hierzu). Hall-Effekt −
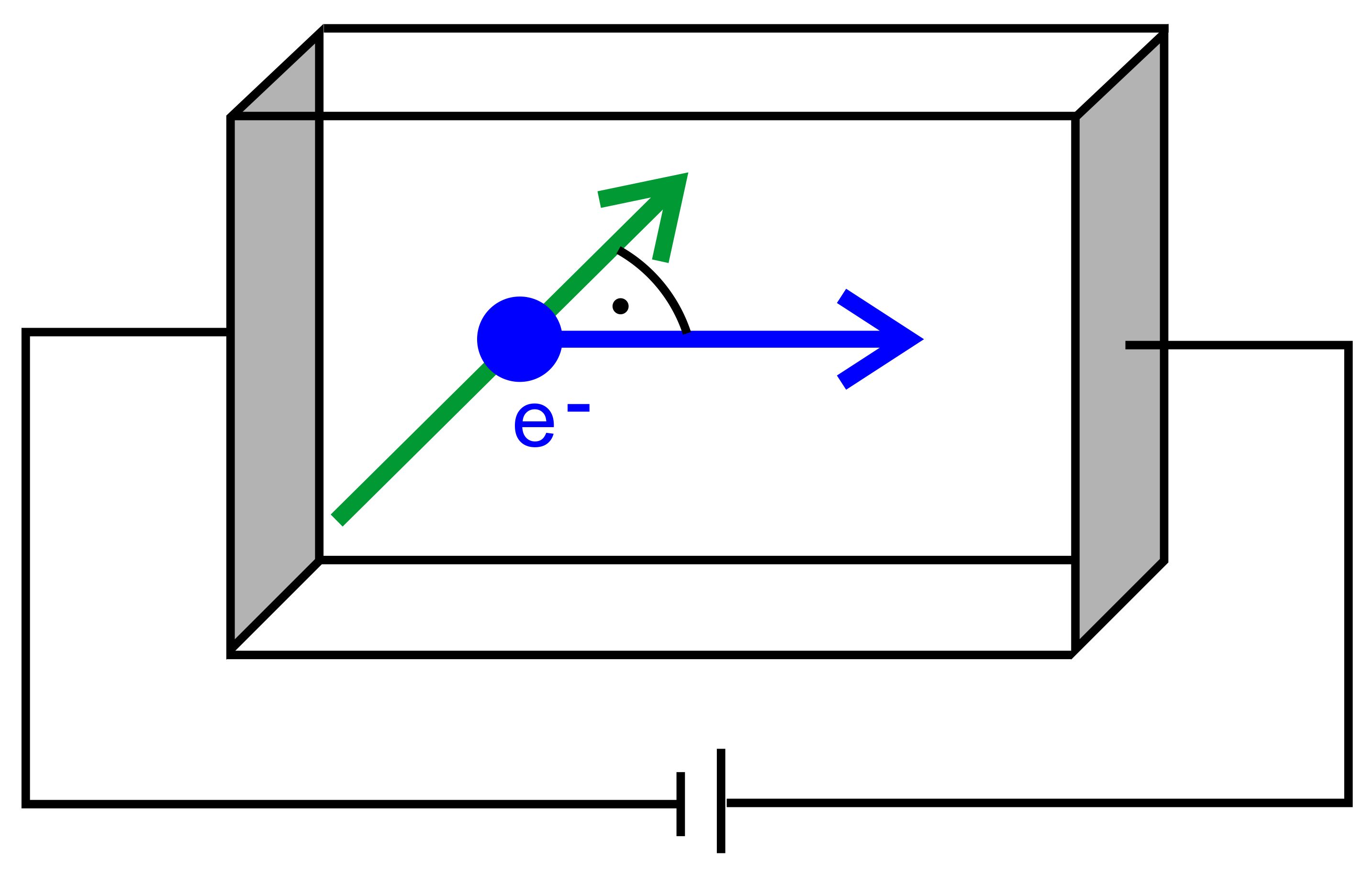
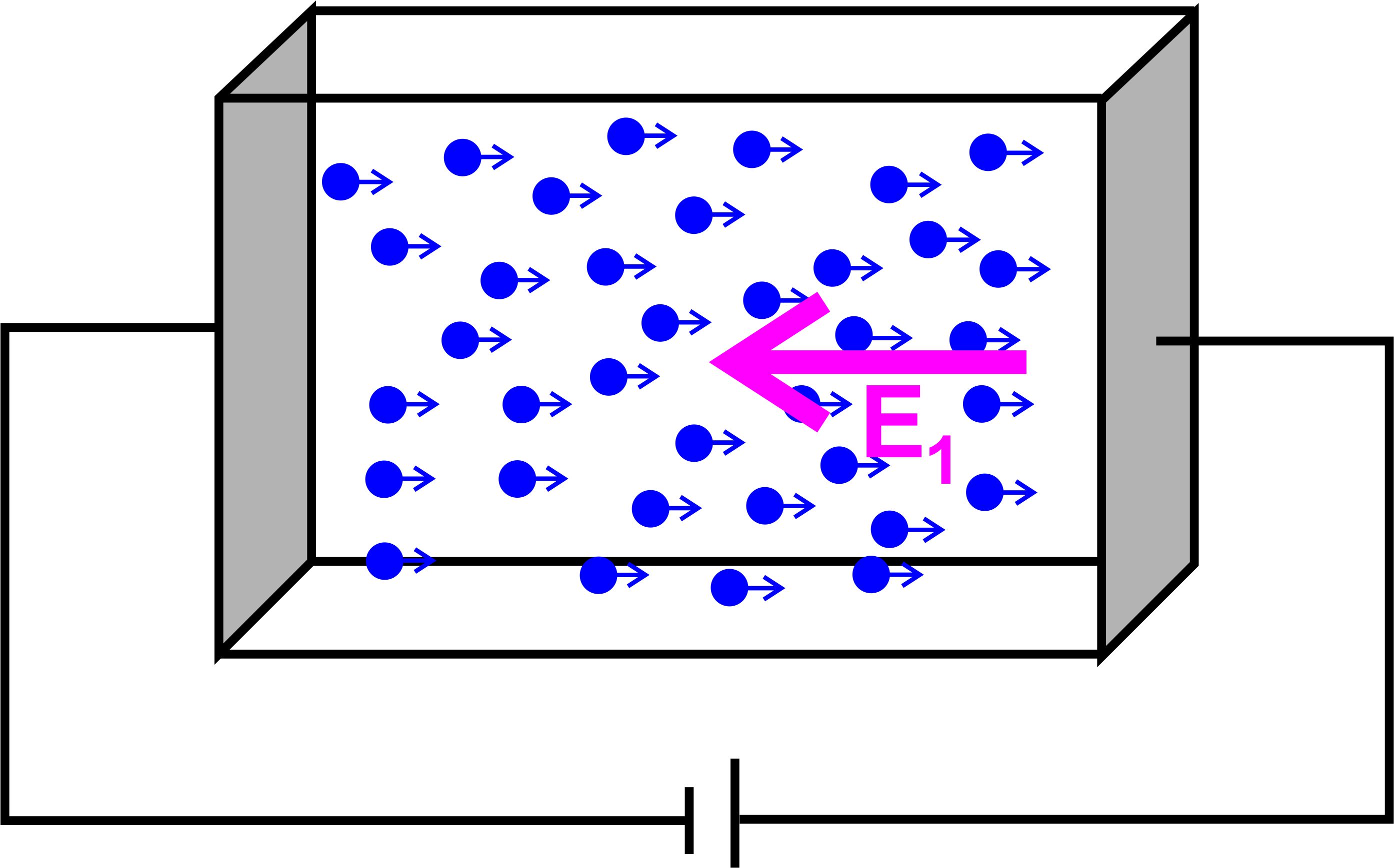
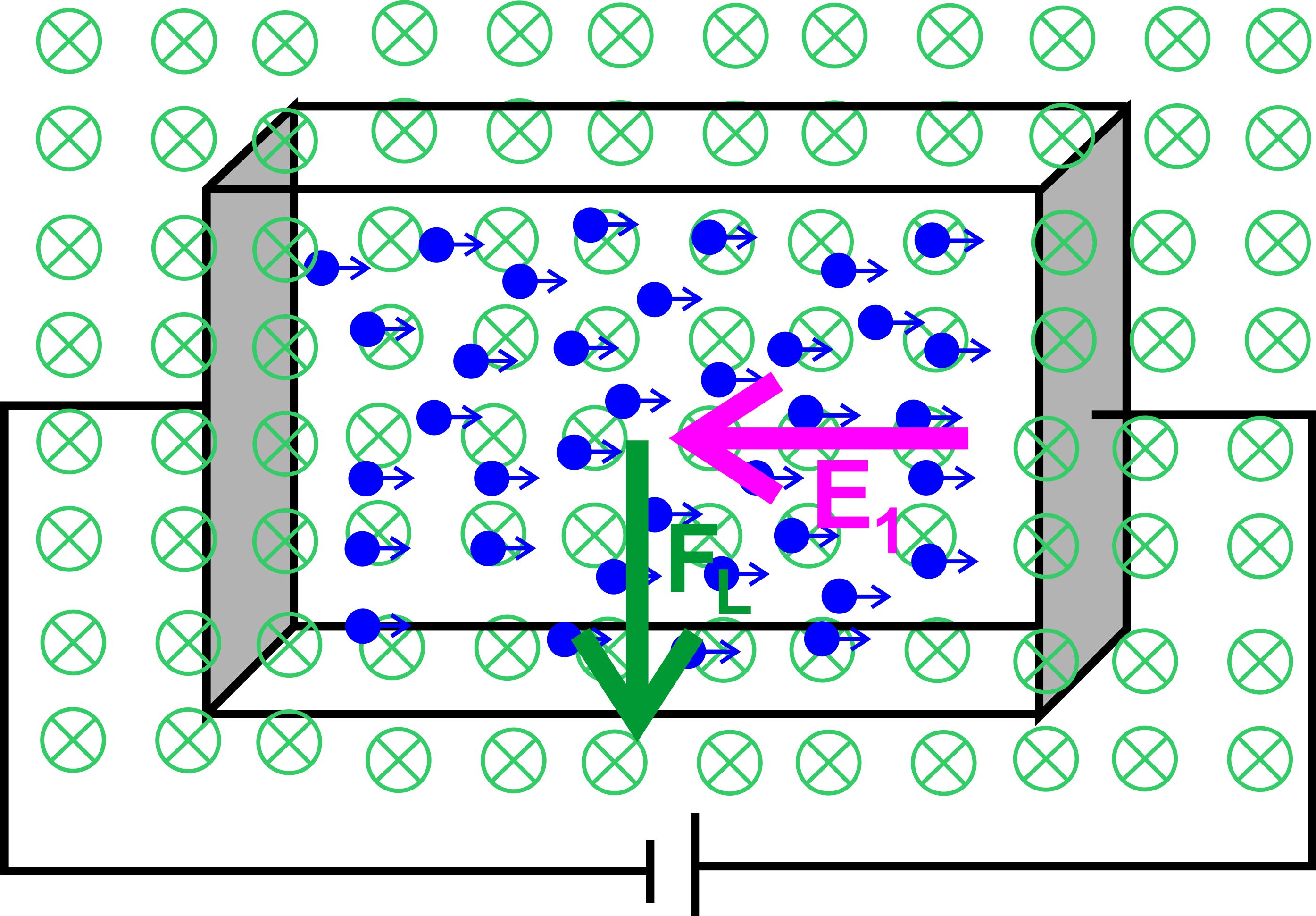
Erklärung 1.
Schritt: Aufbau ohne Magnetfeld Erläuterung
an der Abbildung:
Durch
das Hallplättchen fließt nur ein elektrischer Strom, d.h. die Elektronen
bewegen sich unter dem elektrischen Feld E1, welches durch
die Batterie erzeugt wird, mit ihrer Driftgeschwindigkeit
v vom Minus-Pol
zum Plus-Pol. Wenn die
Seitenflächen(grau) vollständig geladen sind, bewegen sich die
Elektronen innerhalb des Hallplättchens gleichmäßig
verteilt nach rechts. 2.Schritt:
Aufbau mit Magnetfeld Auch
hierzu eine Abbildung:
Das
Magnetfeld steht senkrecht zur Bewegungsrichtung der Elektro- nen. Es
tritt jetzt eine Lorentzkraft FL
auf. Nach der Drei-Finger-Regel zeigt
diese Kraft nach unten. Welche Folgen hat dies? 3.
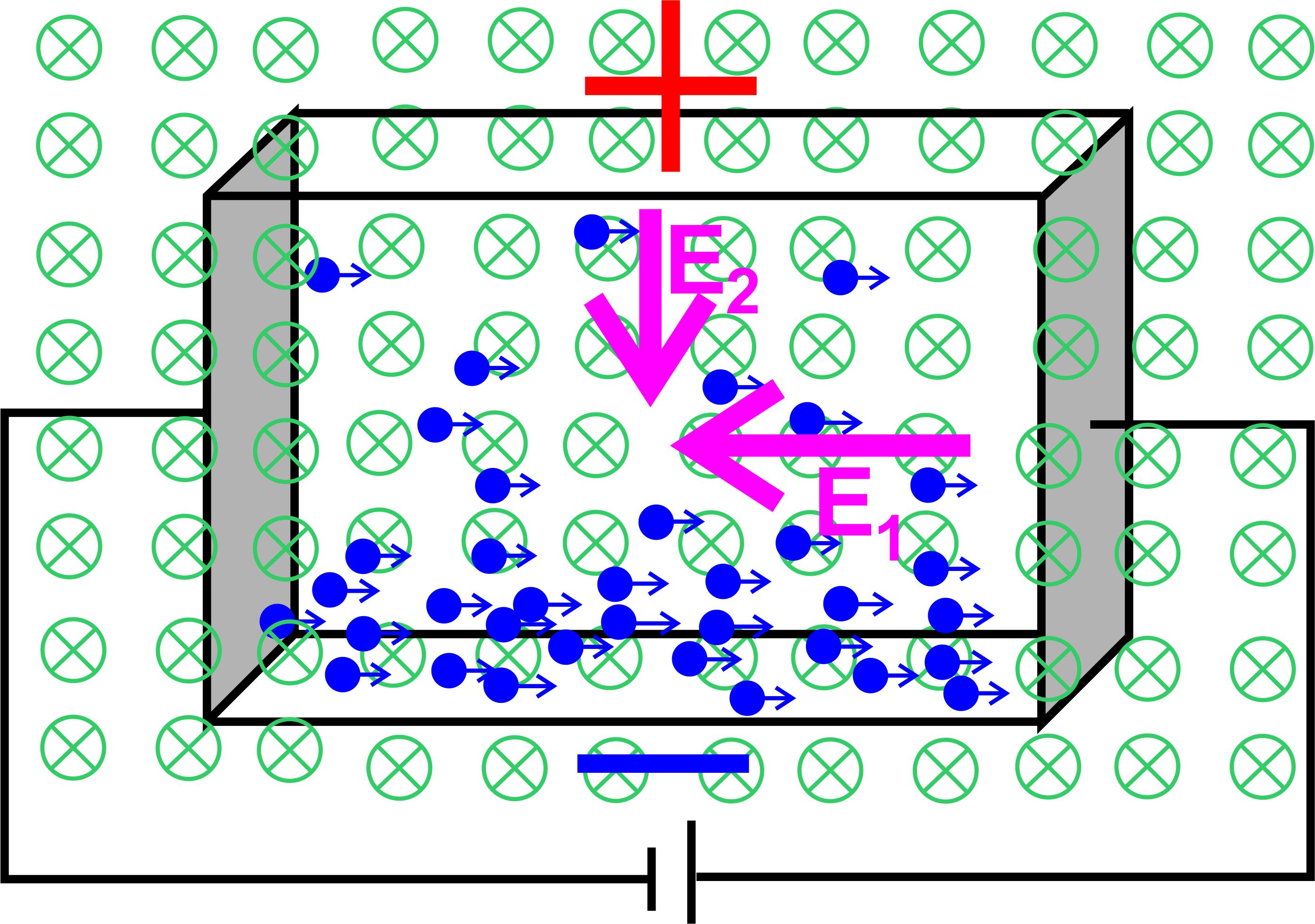
Schritt: Auswirkungen der Lorentzkraft Wieder
zunächst eine Abbildung:
Aufgrund
der Lorentzkraft bewegen sich die Elektronen nach unten, d.h. im
unteren Bereich des Plättchens befinden sich deutlich mehr Elektronen
als im oberen Bereich. Man hat unten einen Elektronen- überschuss
und oben einen Elektronenmangel. Es liegt also eine La- dungsdifferenz
vor. Man erhält unten einen negativen Pol und oben einen
positiven Pol. Der Aufbau ähnelt also sehr einem Kondensator. Zwischen
den „Kondensatorplatten“ (oben-unten) kann somit eine Spannung
abgegriffen werden. Dies ist die Hallspannung. Durch den Ladungsunterschied
baut sich jetzt ein zweites elektrisches
Feld E2 auf.
Dies wird um so größer, je deutlicher der
Ladungsunterschied ist. 4.
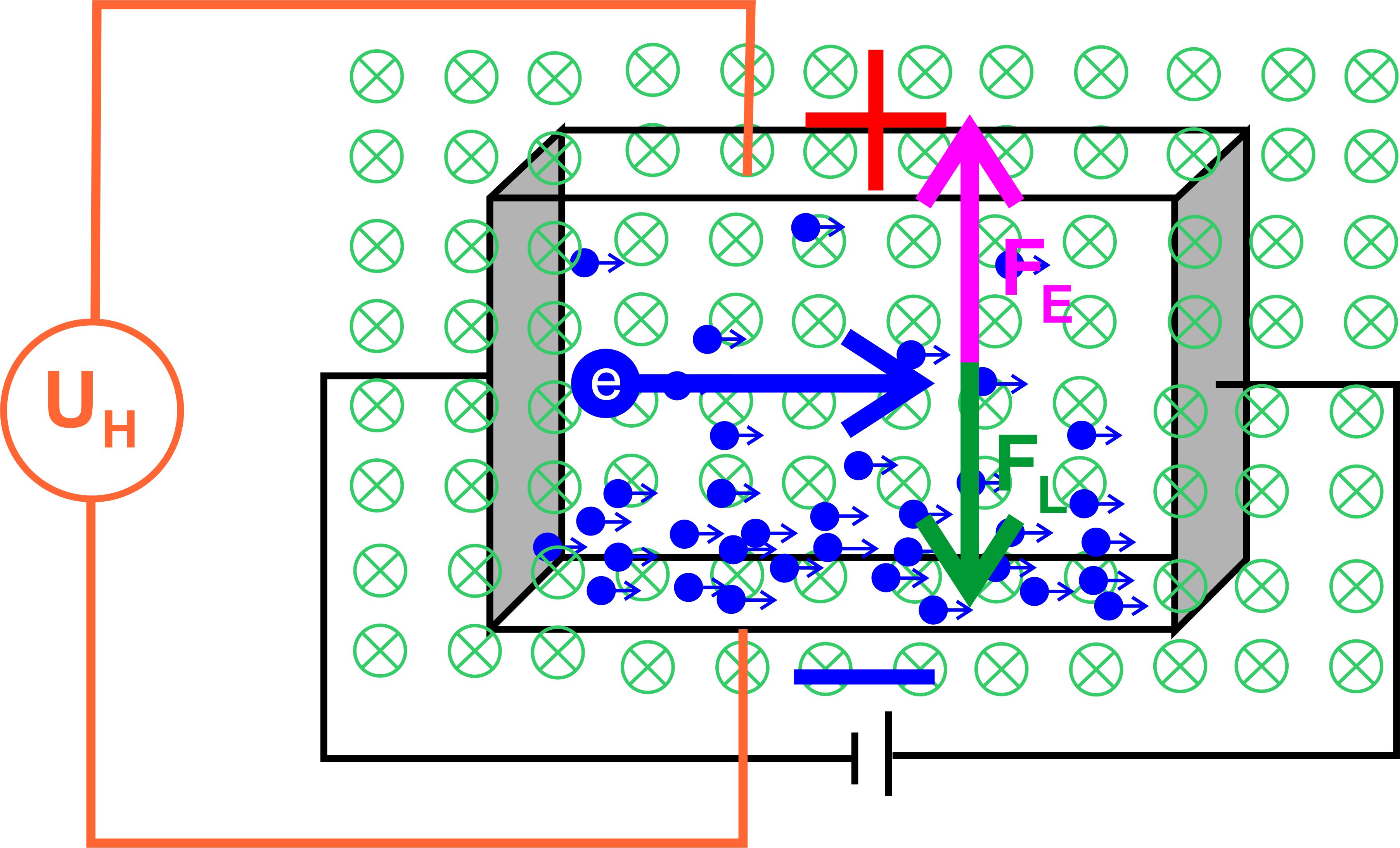
Schritt: Auswirkungen der Ladungsverschiebung Die
Abbildung dazu:
Durch
das zweite elektrische Feld E2 tritt eine elektrische
Feldkraft FE auf, die
der Lorentzkraft entgegengerichtet ist. Sobald sich die beiden Kräfte
ausgleichen, werden keine Elektronen mehr nach unten abge- lenkt,
sondern bewegen sich wieder geradlinig durch das Plättchen. Jetzt
ändert sich auch nichts mehr an der Hallspannung. Diese bleibt konstant.
Der ganze Ablauf erfolgt in sehr kurzer Zeit, so dass man im Versuch
sofort die Hallspannung abgreifen kann. Im Folgenden sieht man eine Darstellung des 4. Schrittes in einer GeoGebra-Animation:
Quelle: Schulphysikwiki Hinweis: mit der rechten Maustaste kann man die
Abbildung im Raum bewegen! Es werden hier
positive Ladungen betrachtet! Hall-Effekt −
Messungen Im
Folgenden werden meine Messungen im LK 14-15 benutzt. Zunächst
muss die Anzeige am Voltmeter für die Hallspannung auf Null
eingestellt werden, wenn noch kein B-Feld vorliegt, d.h. es darf noch
kein Strom durch die Spulen fließen. Dies geschieht mit den eingebauten
Potentiometern. Da
man die Anschlüsse für das Abgrei- fen der
Hallspannung nie exakt gegenüber anbringen kann, kann schon
eine Spannung (Potentialdifferenz) durch das elektrische Feld E1
auftreten. Diese muss zunächst „kompensiert“ werden. Jetzt
kann man das Magnetfeld erzeugen, indem man die Spulen mit Strom versorgt.
Das Magnetfeld wird auch auf die Polschuhe über- tragen,
so dass das Hallplättchen von dem Magnetfeld senkrecht durchsetzt wird. Man
kann jetzt am Voltmeter eine sehr geringe Span- nung
ablesen. Diese Spannung kann in Abhängigkeit von der Strom- stärke
im Hallplättchen (ISpule = konstant) und
in Abhängigkeit von der Spulenstromstärke
(IHall = konstant) untersucht werden. Hierzu
meine Messwerte:
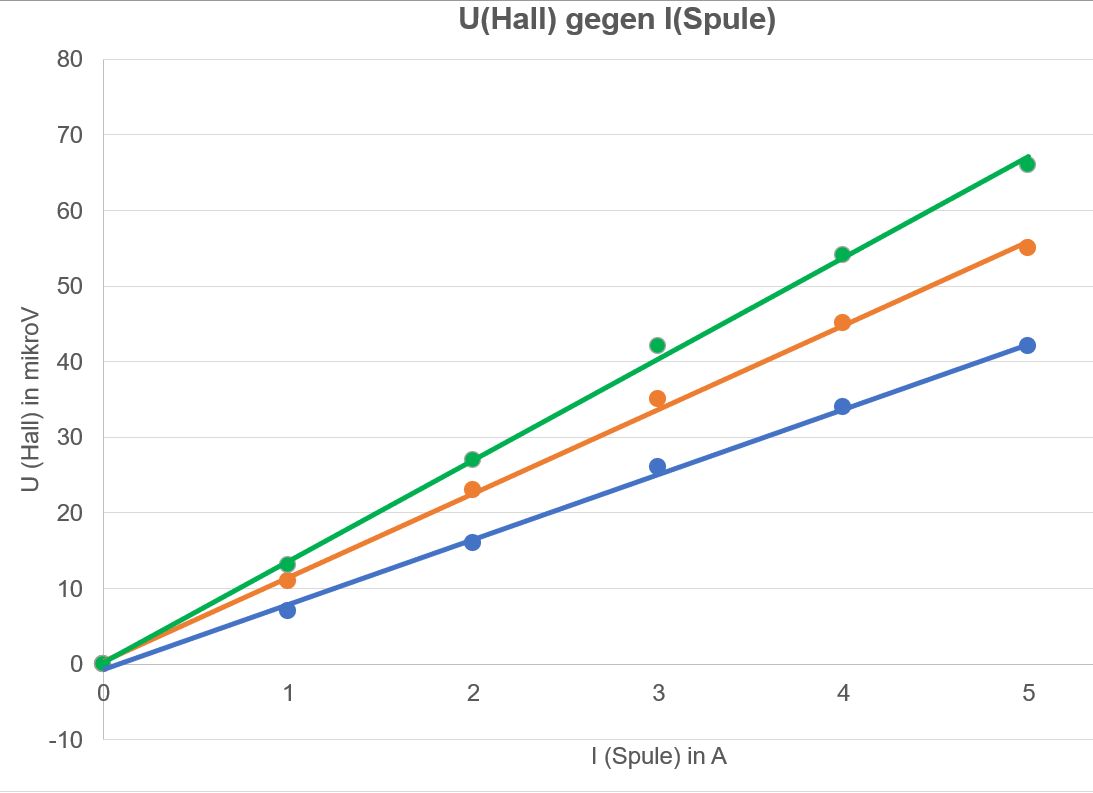
1. Fall:
UHall wird gegen ISpule
aufgetragen
Man
erkennt sofort, dass in allen drei Fällen Ursprungsgeraden ent-stehen, d.h. es liegt
eine Proportionalität zwischen UHall und ISpule
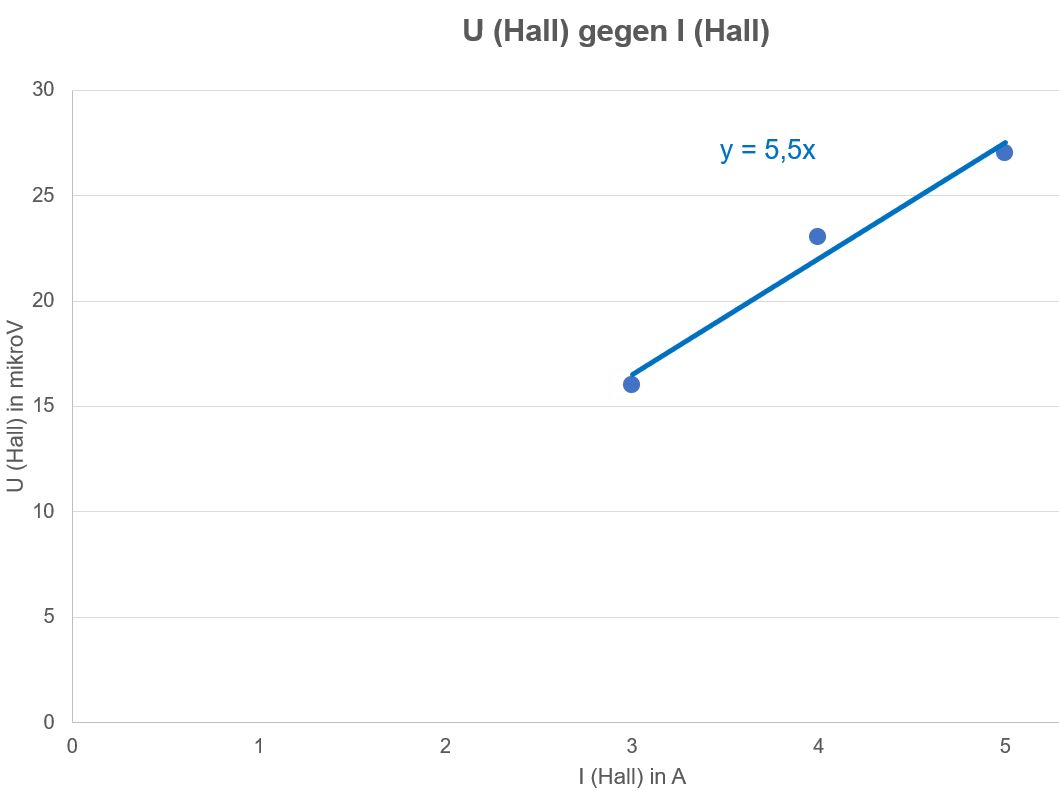
vor. 2. Fall:
UHall gegen IHall
(bei ISpule = 2 A ).
Hinweis: die Anzahl der Messwerte ist recht gering.
Man
erkennt an der Formel, dass auch hier eine Ursprungsgerade vor- liegt, d.h. auch hier gibt es eine Proportionalität zwischen UHall
und IHall. Hall-Effekt −
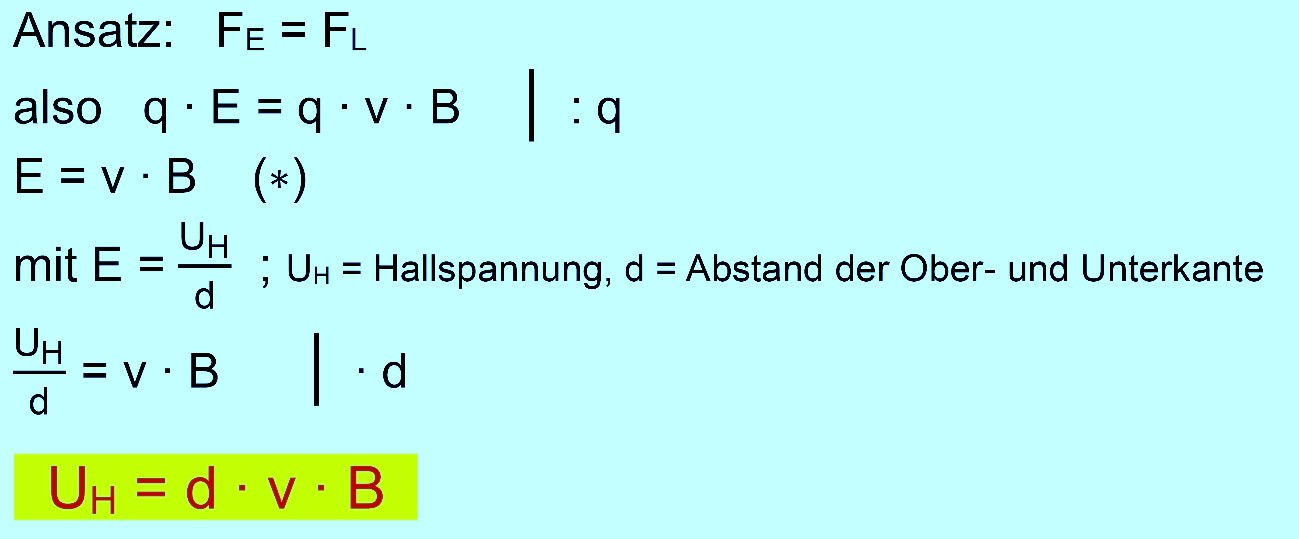
Formeln Wir
wollen jetzt einmal die Formeln kennenlernen, die beim Halleffekt eine
große Rolle spielen und damit die Messergebnisse vergleichen. Ausgangspunkt der Überlegungen ist unser 4. Schritt, bei dem die beiden Kräfte FE und FL gleich groß sind.
Wir haben jetzt also eine Formel zur Bestimmung der Hallspannung. Hinwies: An der Formel (*) erkennt man, dass im Aufbau große Ähnlichkeiten zum
Wienfilter vorliegen. Wir fassen also zusammen:
Passt
dies zu den Messergebnissen? UH
ist nach den Messergebnissen proportional zu ISpule
bzw. IHall. Obwohl
wir an dieser Stelle noch keine Formel für die Magnetfeld- stärke
einer Spule kennen, kann man wohl davon ausgehen, dass die Stromstärke
ISpule proportional zu B sein wird. Dies
würde dann be- deuten,
dass UH proportional zu B wäre, was mit der Formel im Ein- klang
ist. v dürfte
proportional zu IHall sein, so dass auch
hier eine Übereinstim- mung zu den Messwerten auftritt (s. auch nächste
Formel). Halleffekt−Vertiefung:
Hallkonstante Wenn man
das Thema „Halleffekt“ noch vertiefen will, kann man eine Formel
zwischen UH und der Ladungsträgerdichte N nachschieben. Das
sieht dann so aus:
Also
eine weitere Formel für die Hallspannung lautet:
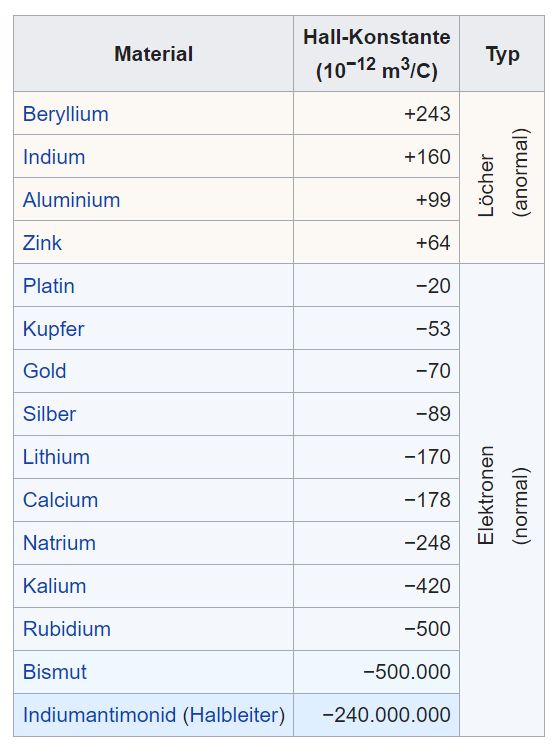
Die Hallkonstante ist eine materialabhängige Größe.
In der folgenden Abbildung aus wikipedia sieht man
ein paar Beispiele für die Hall- konstanten:
Quelle: wikipedia Man
sieht, dass Silber im Vergleich zu Bismut einen wesentlich klei- neren
Wert aufweist, so dass man im Schulversuch deutlich höhere Hall-Stromstärken
benutzen muss, um eine Spannung messen zu Hallsonde Die Hallsonde
ist ein Messgerät zur Bestimmung von magnetischen Feldstärken.
Die Sonde benutzt hierzu den Halleffekt. Es werden Materialien
mit extrem hohen Hallkonstanten, also Halbleiter, verwen- det.
Alle Firmen, die Versuchsaufbauten für die Schule vertreiben, bieten
natürlich solche Sonden an. Hiermit kann man dann Magnetfel- der verschiedener Aufbauten (Spule, langer Leiter) ausmessen und Formeln
für die Bestimmung von B aufstellen (s.dort). Der
Vorteil einer Hallsonde ist, dass sie nicht aus ferromagnetischem Material
besteht und somit das Magnetfeld nicht verändert. Die
Hallsonde muss natürlich zunächst vom Hersteller geeicht werden, bevor
sie zum Einsatz kommen kann. Bestimmung
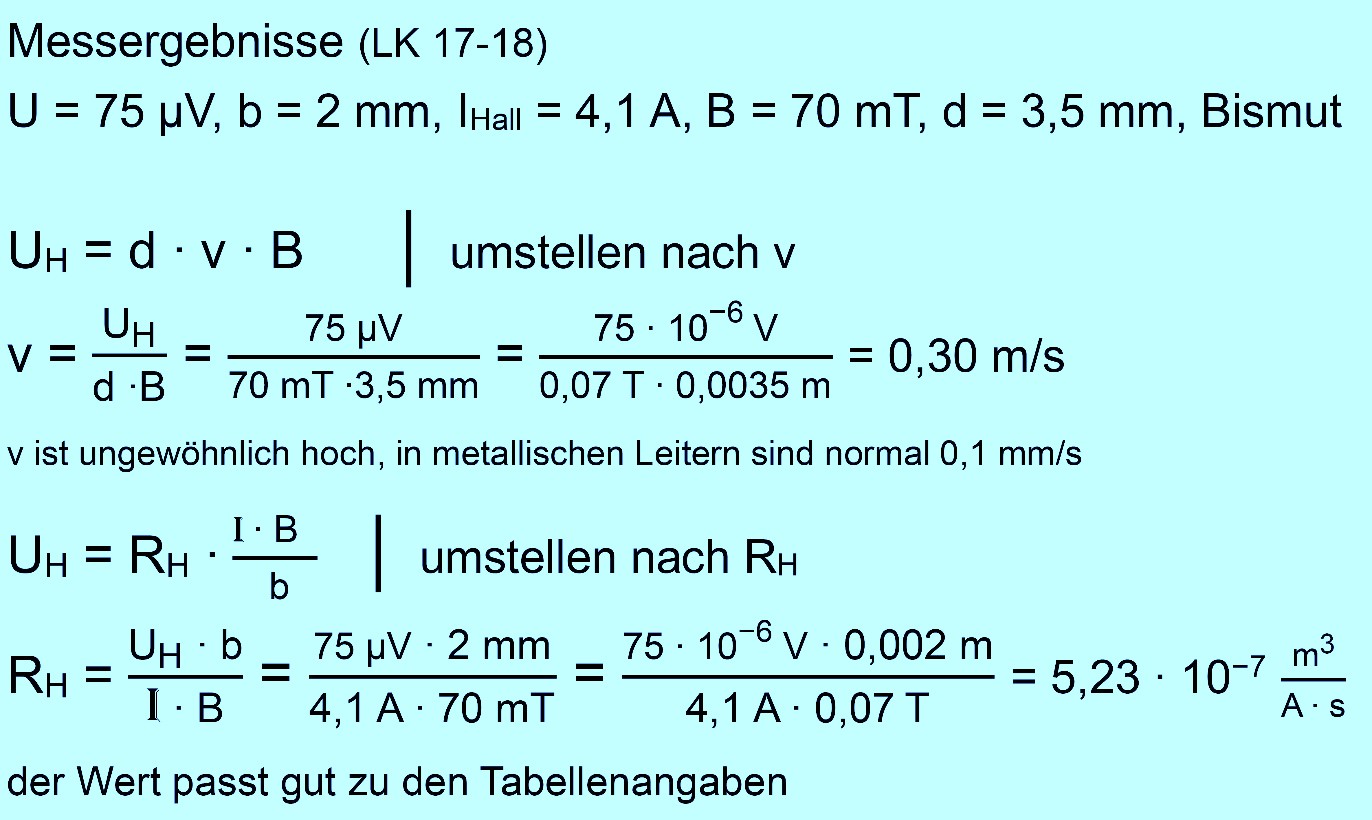
der Hallkonstanten für Bismut Wenn man
eine Hallsonde zur Verfügung hat, ist es jetzt auch möglich die
Hallkonstante und die Driftgeschwindigkeit zu berechnen, da man jetzt B
bestimmen kann.
zurück zum Abschnitt:
zum vorherigen Kapitel: zum nächsten Kapitel |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||