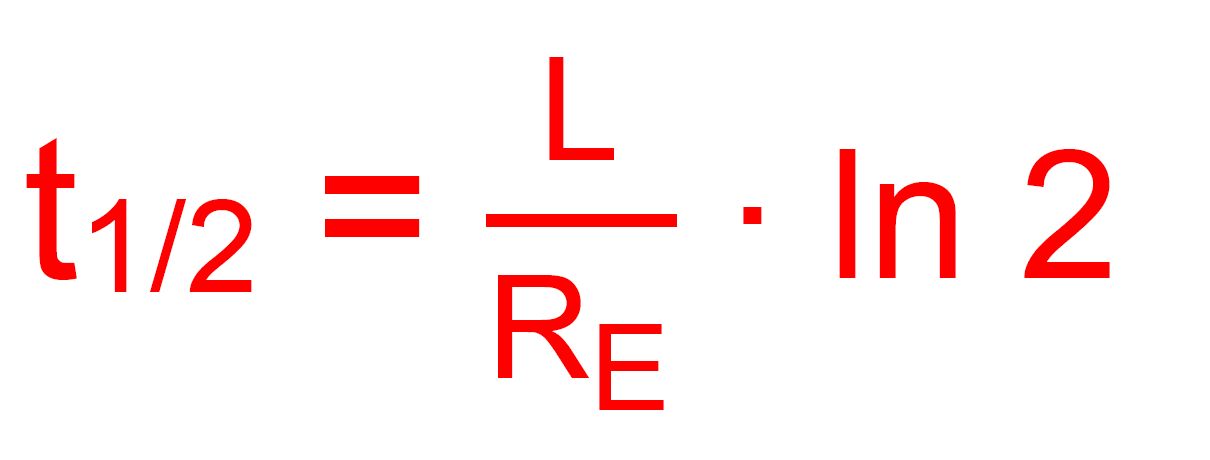|
gehe zu: Zusammenfassung:
Graphen:
Ein- und Ausschalten Im
Folgenden wollen wir noch einmal zusammenfassen, welche Funktionen
den Ein- und Ausschaltprozess bei der Spule bestimmen. Wir
sehen uns noch einmal die Graphen zu den Funktionen an und sprechen
über Besonderheiten. Außerdem wird ein Experiment zur Bestimmung
der Graphen mit dem Oszilloskop vorgestellt.
Wir
haben in den einzelnen Kapiteln zum Einschalten
und Ausschalten die
Formeln für die jeweiligen Prozesse hergeleitet. Es ergab sich: Einschalten
Ausschalten
Schauen
wir uns einmal die Graphen zu den jeweiligen Funktionen an. Es wird
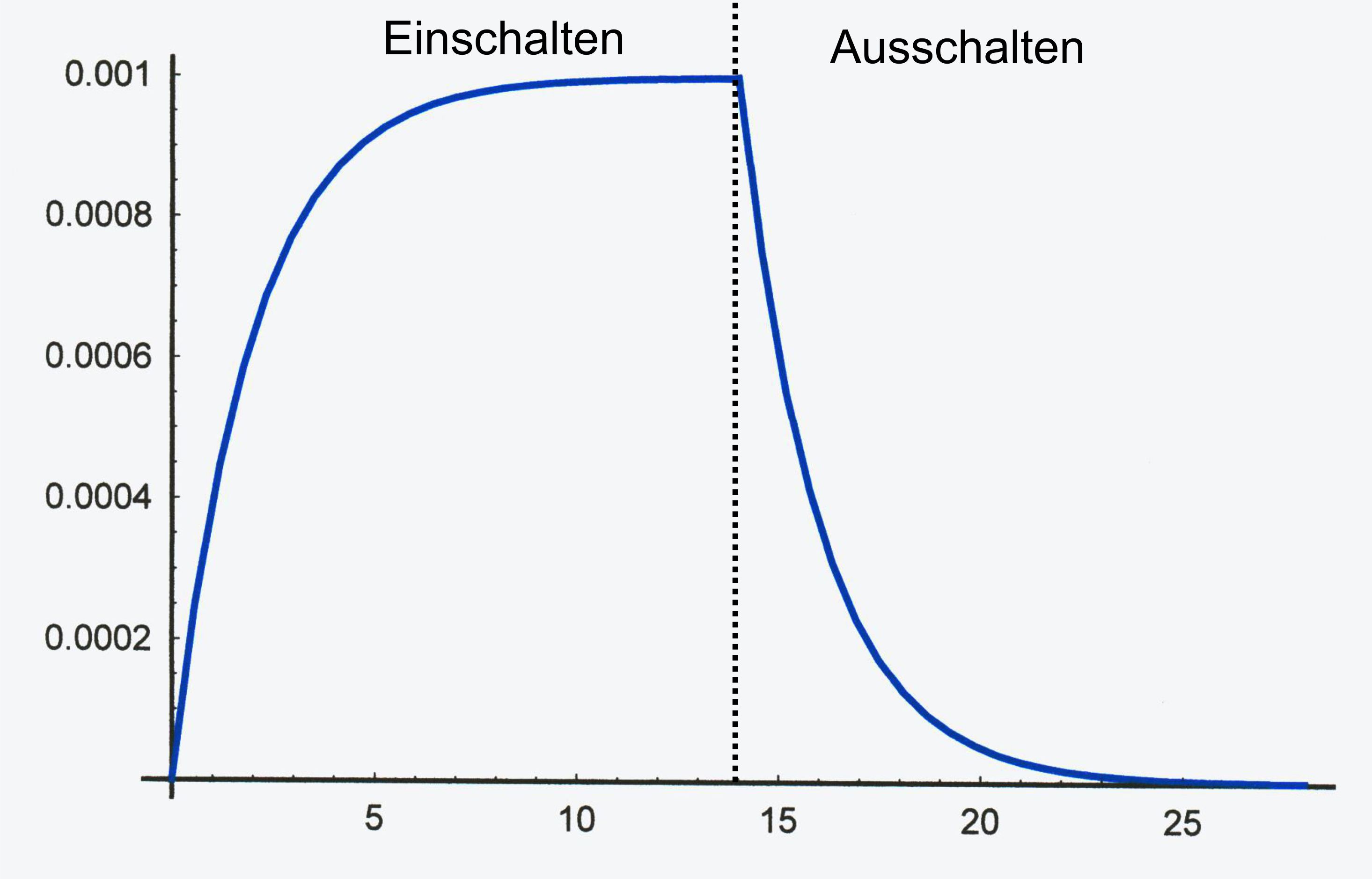
der Fall a.) L =
20000 H, RE = RA = 10 kΩ, U0 = 10 V b.) L =
20000 H, RE = 10 kΩ, U0 = 10 V; RA =
190 kΩ >> RE gezeigt. a.) Stromstärke:
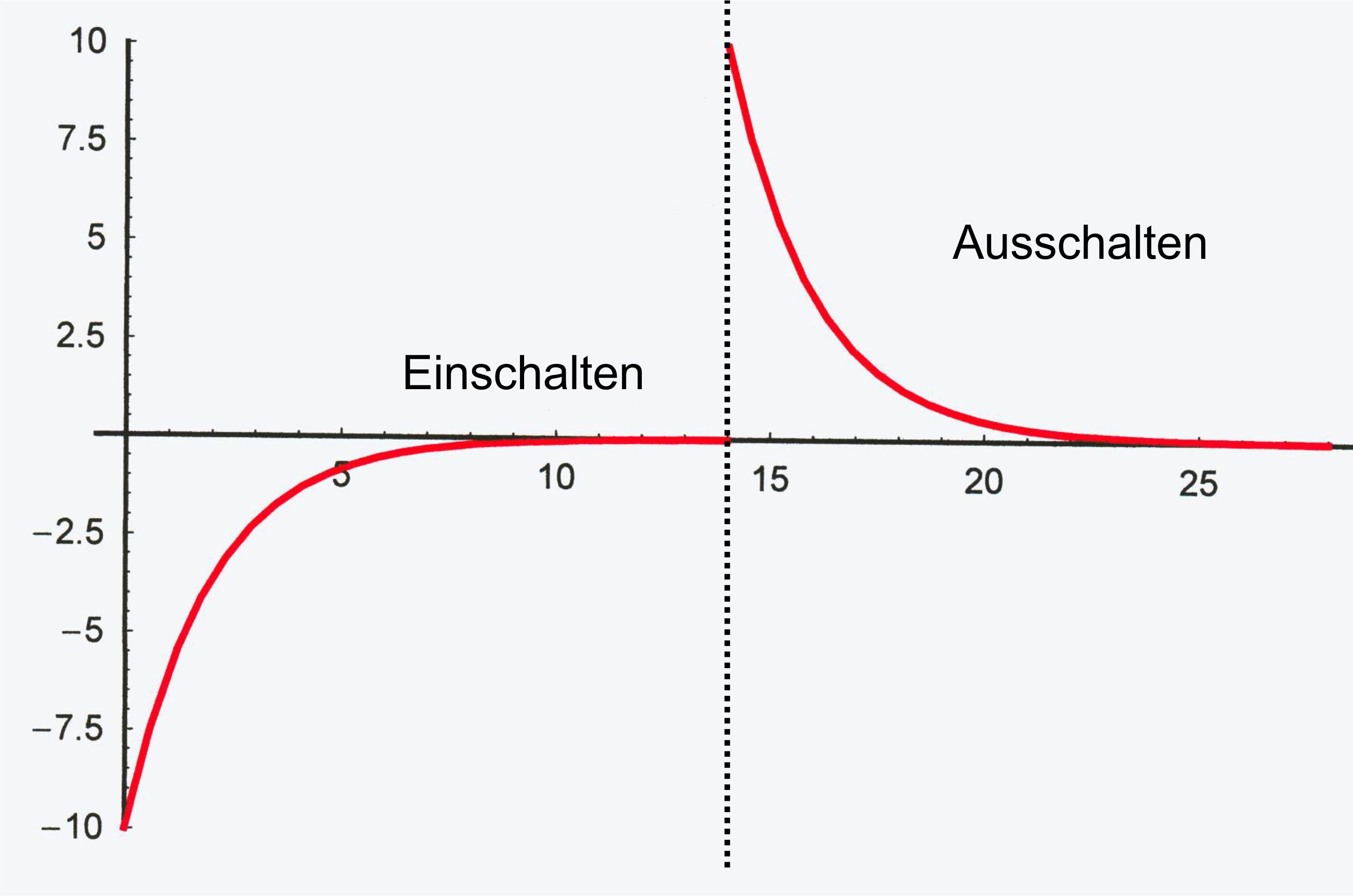
Induktionsspannung:
Die
Graphen sehen bei RE = RA recht „symmetrisch“ aus. Die Lenzsche Regel gilt. Einschalten:
der Anstieg der Stromstärke wird behindert, indem die Induktionsspannung
der äußeren Spannung entgegenwirkt. Ausschalten:
die Stromstärke soll aufrechterhalten bleiben, indem die
Induktionsspannung den Stromfluss unterstützt. Der Abfall erfolgt trotzdem
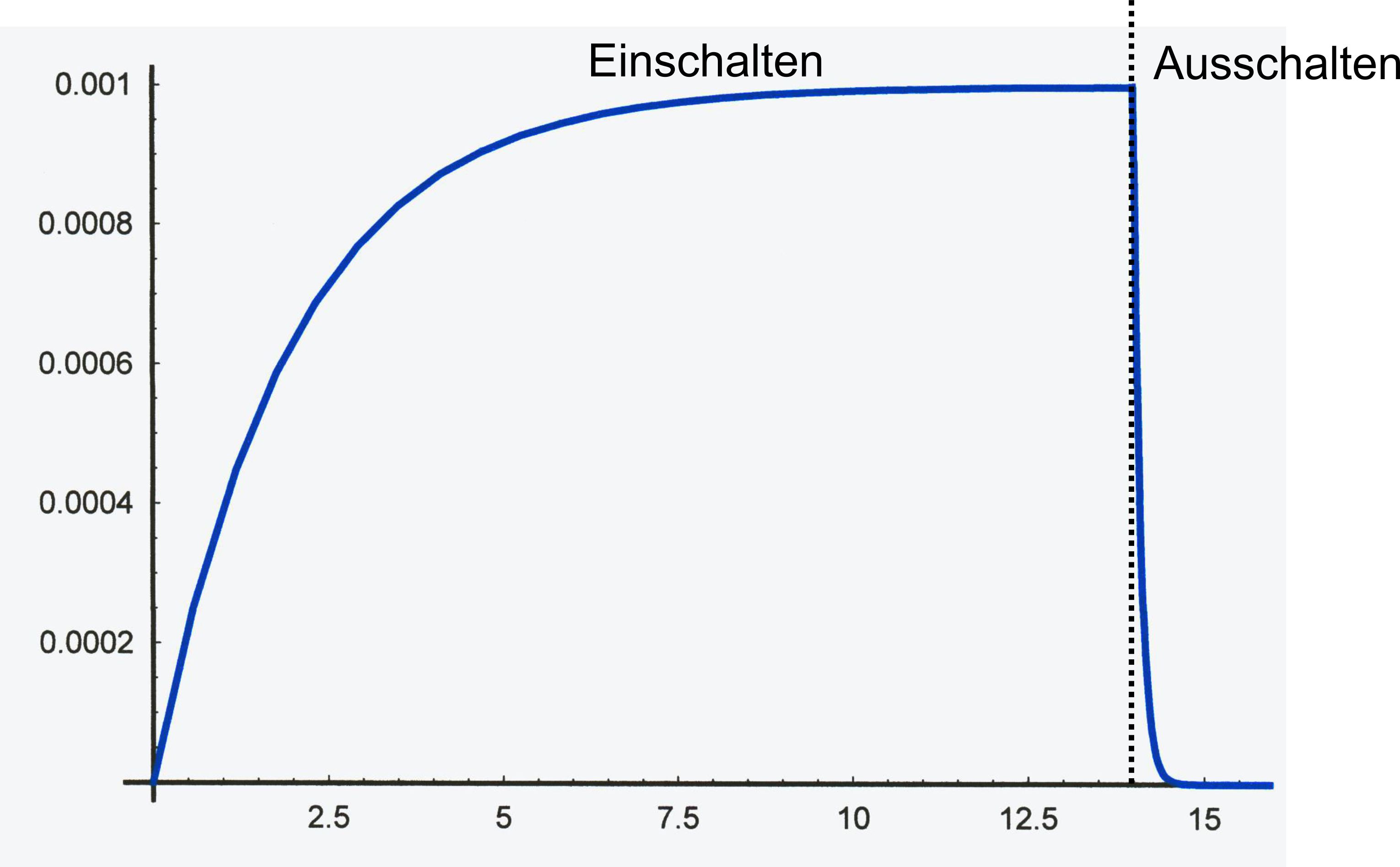
recht schnell. b.) Stromstärke:
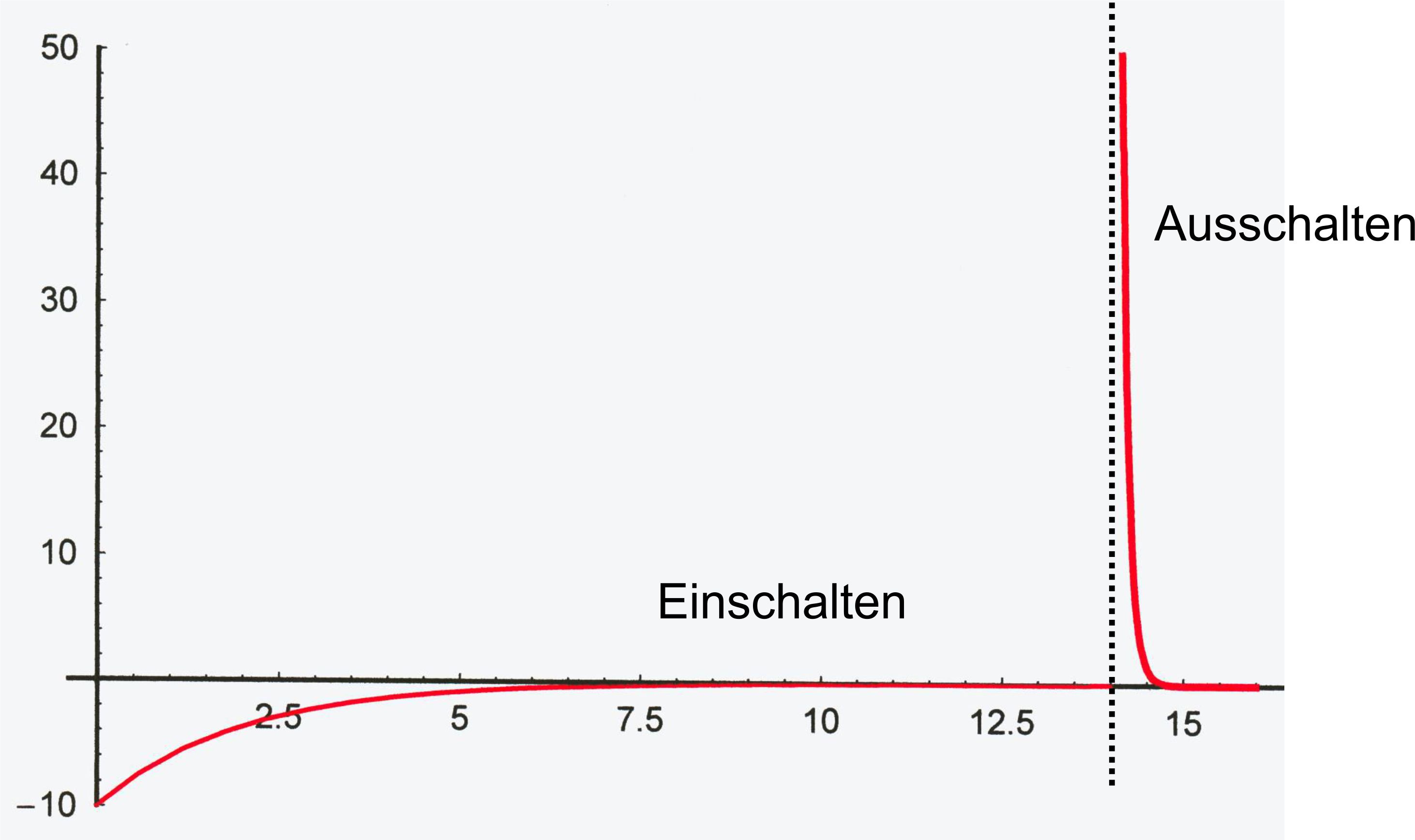
Induktionsspannung:
Für RA>>RE
liegt keine Symmetrie mehr vor. Beim
Einschalten haben wir die Verhältnisse wie bei a.). Beim Aus- schalten
ergeben sich aber viel extremere Verhältnisse als bei a.), vor allem
die Induktionsspannung ist anfangs deutlich höher (max. 200 V). Um die Schnelligkeit der Einschalt- bzw. Ausschaltphase zu beurteilen wird häufig die Halbwertszeit gewählt.
Wenn die Größe f durch eine Exponentialfunktion beschrieben wird, ist die HWZ für jeden Zeitpunkt t eine konstante Zeit, da ja die Grund- eigenschaft einer Exponentialfunktion gilt, d.h. at + b = at ∙ ab egal welches t vorliegt. Wir bestimmen jetzt einmal die HWZ für den Ausschaltprozess:
Für die obigen Beispiele ergibt sich: a.) t1/2 = 1,4 s und b.) t1/2 = 0,07 s Bei sehr hohem Ausschaltwiderstand ergibt sich eine sehr kurze HWZ. Beim Einschaltvorgang ergibt sich eine analoge Formel, wenn man als HWZ die Zeit wählt, um den Abstand zum Maximalwert zu halbier- en. Es gilt dann:
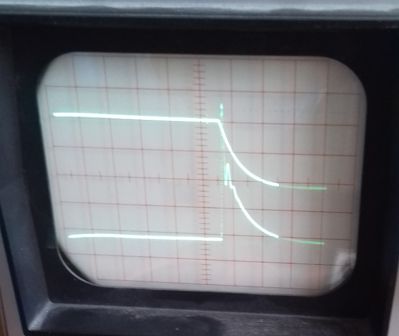
Experiment zur Bestimmung der Graphen Um die Graphen des Ein- und Ausschaltvorgangs sichtbar zu machen, kann man sich eines Oszilloskops bedienen. Man kann sich folgenden Aufbaus durchführen.
Im Folgenden sieht man den von mir benutzten Aufbau.
Konkret wurden benutzt: 2 Leyboldspulen (n = 10000, L = 4,46 H) R = 5 kΩ, Leybold-Funktionsgenerator Zusatzmaterial
Weiteres Zusatzmaterial:
Auch hier gibt es schöne Diagramme (gut
erläutert): 0:00 bis 2:00 Verlauf der Stromstärke;
17:40 bis 20:00 Verlauf der Induktionsspannung auch in Abhän- gigkeit
vom Ausschaltwiderstand !!! 2:00 bis 17:40
Theorie (s. bei mir oben); 20:10
bis 21:30 Zündung einer Glimmlampe ( s. bei
mir: Anwendungen); ab 21:30 eine angebliche Anwendung am Weidezaun: ist zwar witzig, aber
falsch, da hier aus Sicherheitsgründen ein Trafo benutzt wird
gehe zu: zurück
zum Kapitel: weiter
zum Kapitel: Anwendungen der
Selbstinduktion zurück zur Übersicht „Induktion“ |