|
Exkurs:
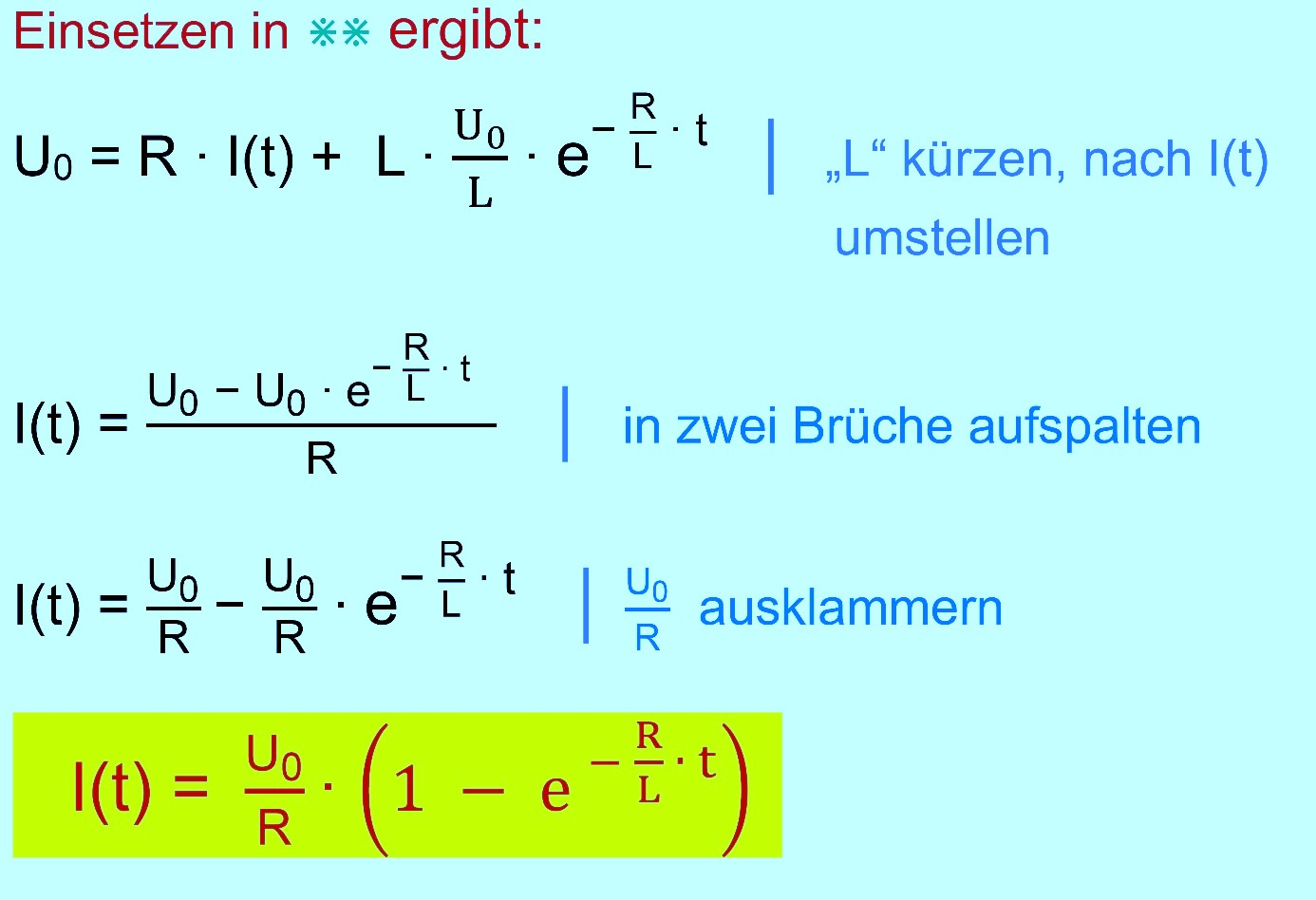
Sättigungskurve−Mathematik Wir wollen jetzt einmal mathematisch herausfinden, welcher Funk-tionsterm beim Einschalten der Spule vorliegt, d.h. welche Funktion beschreibt eigentlich unsere Sättigungskurve. Hinweis:
dieses Thema ist im Wesentlichen nur für den LK geeignet, da bei der
Integration die
Substitutionsregel bekannt sein muss. Außerdem wird auf den natürlichen
Logarithmus und die
e-funktion eingegangen. Weitere
mathematische Einordnung: Es
müssen homogene und inhomogenen (gewöhnliche) Differentialgleichungen 1. und
2. Ordnung mit konstanten Koeffizienten gelöst werden. Einführung Wir lösen zunächst einmal ganz allgemein eine gewöhnliche homo- gene Differentialgleichung (DGL) erster Ordnung mit konstantem Koeffizienten. Dies geht noch einigermaßen einfach. Die DGL sieht also folgendermaßen
aus: y`
+ k ∙ y = 0 Es gilt dann, wenn man für y = f(t) setzt:
Wir fassen zusammen:
Zusammenfassung
Übertragung auf den Einschaltvorgang Wir kommen jetzt auf den physikalischen Sachverhalt zurück.
Es geht um den Einschaltvorgang, wenn
sich eine Spule im Stromkreis befindet. Der Stromkreis soll nur aus einer Spule mit der
Induktivität L und einem ohmschen Widerstand R bestehen. Die ange- schlossene Spannungsquelle habe die Spannung
U0. Es gilt dann:
Zusammenfassung
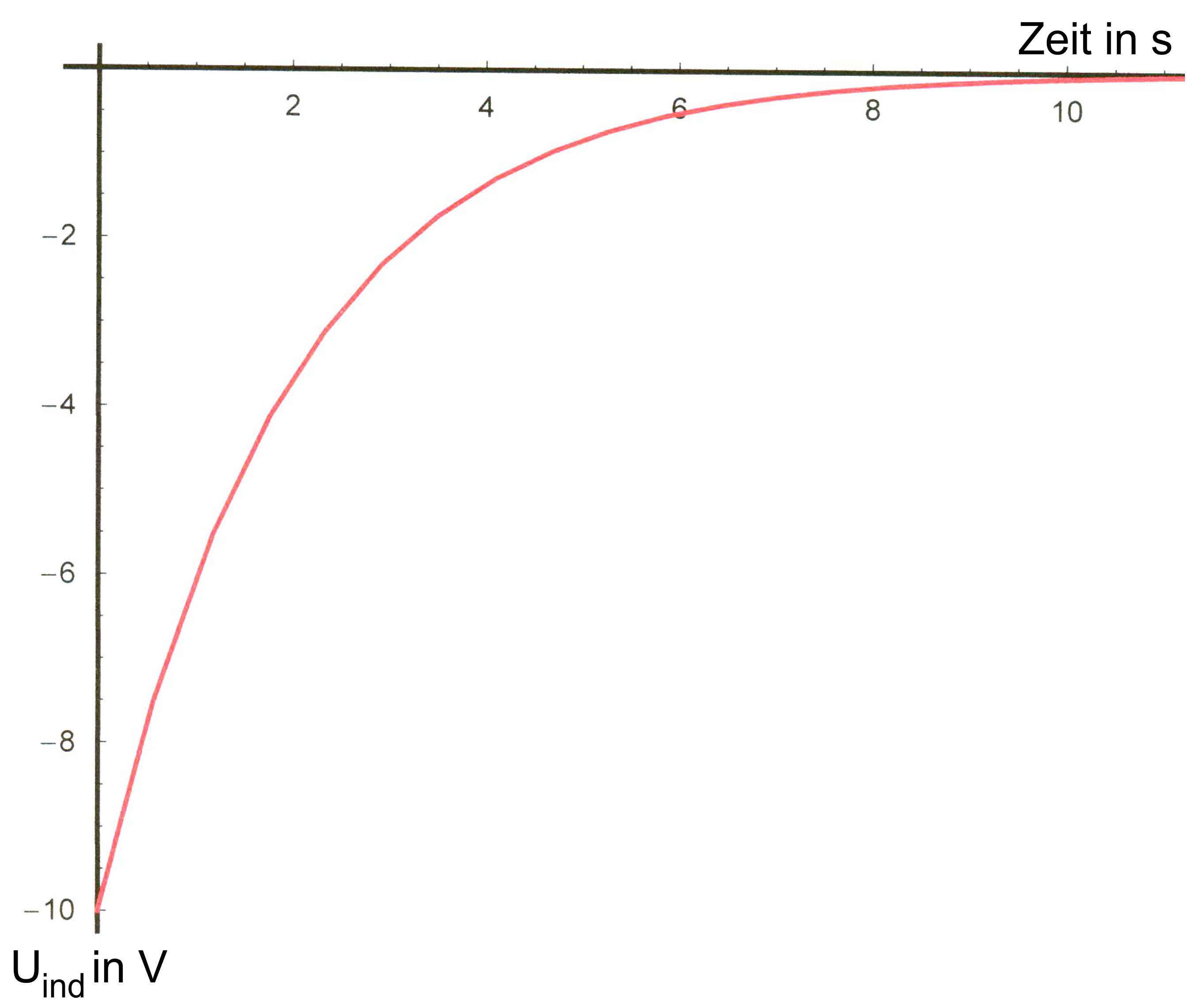
Beispiel Diagramme Wir
lassen einmal die entsprechenden Verläufe für den Fall U0
= 10 V, R = 10 kΩ und L = 20 000 H (s.
Klausuraufgabe) zeichnen.
zurück zum Kapitel „Selbstinduktion−Einschalten“ zurück
zur Übersicht „Induktion“ |