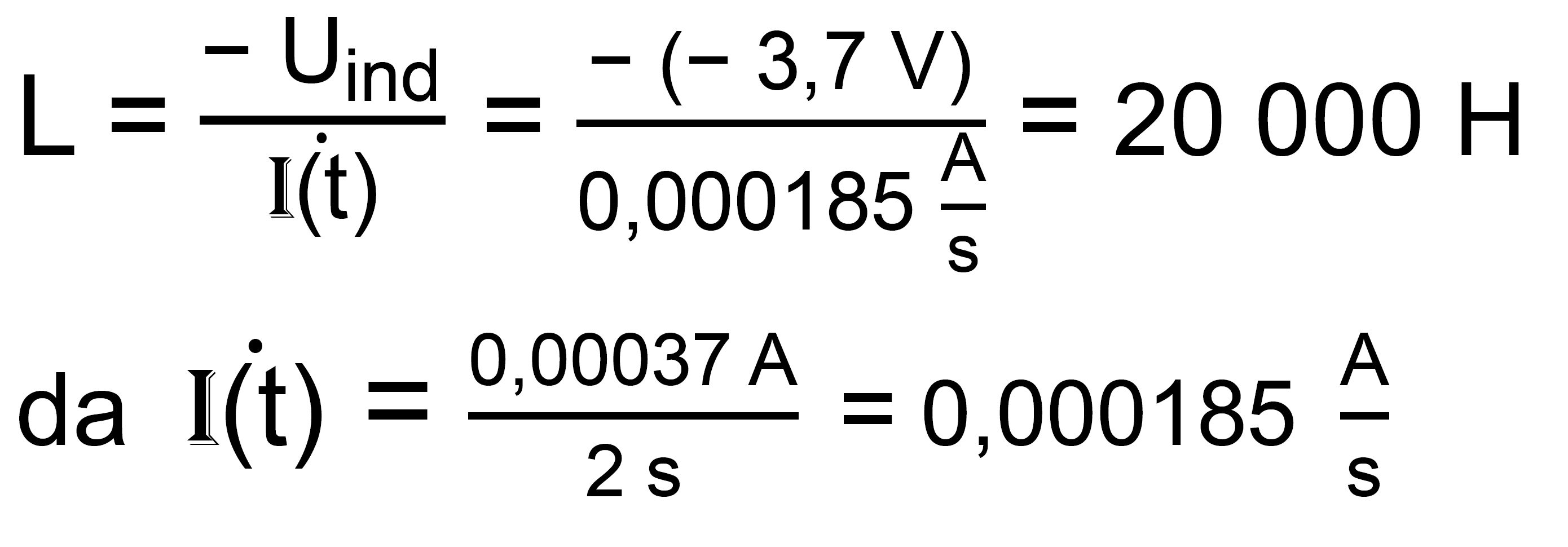Klausuraufgaben

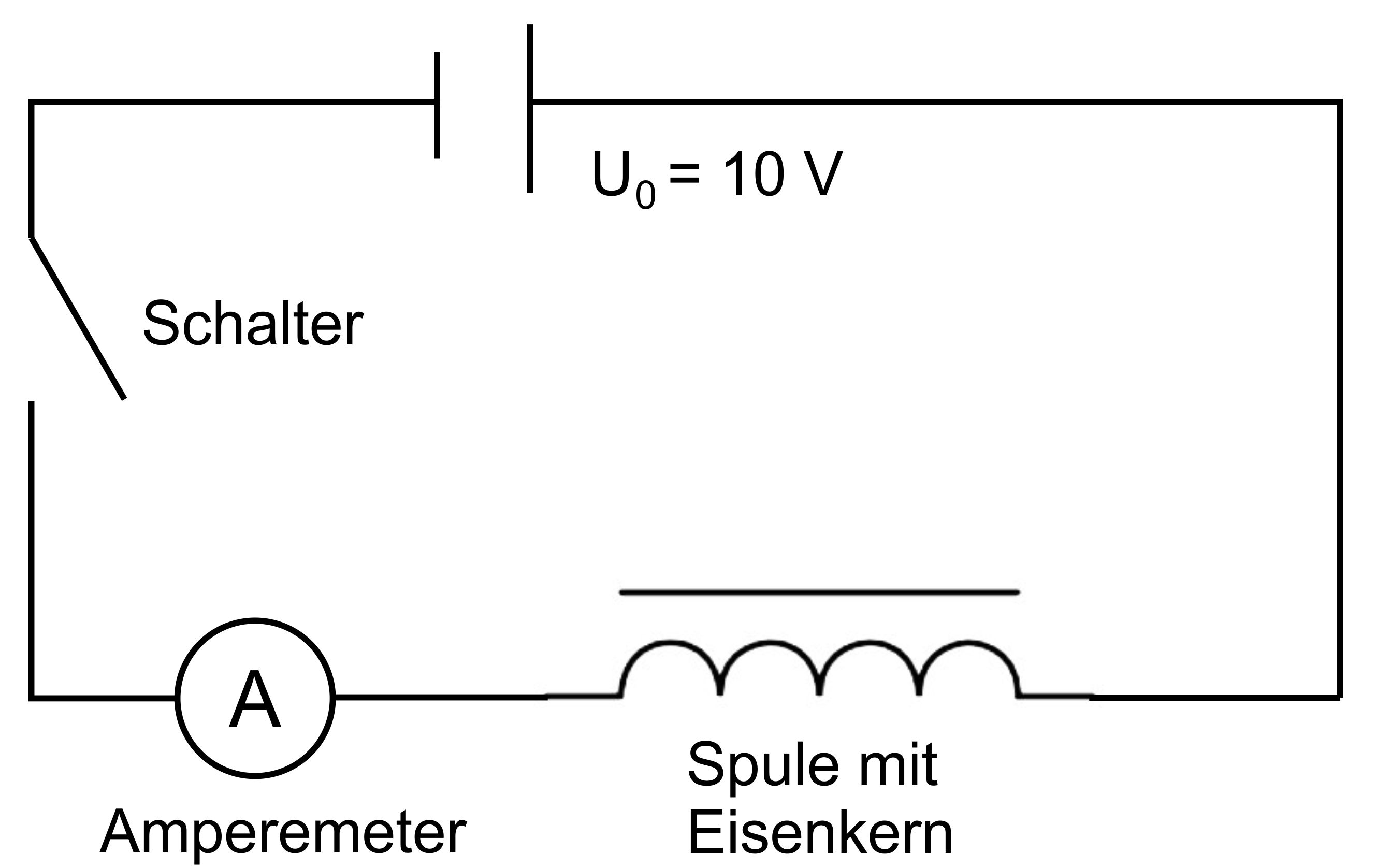
Aufgabe Nr.1 (GK)

Folgender Aufbau ( s. Abbildung) liegt vor.

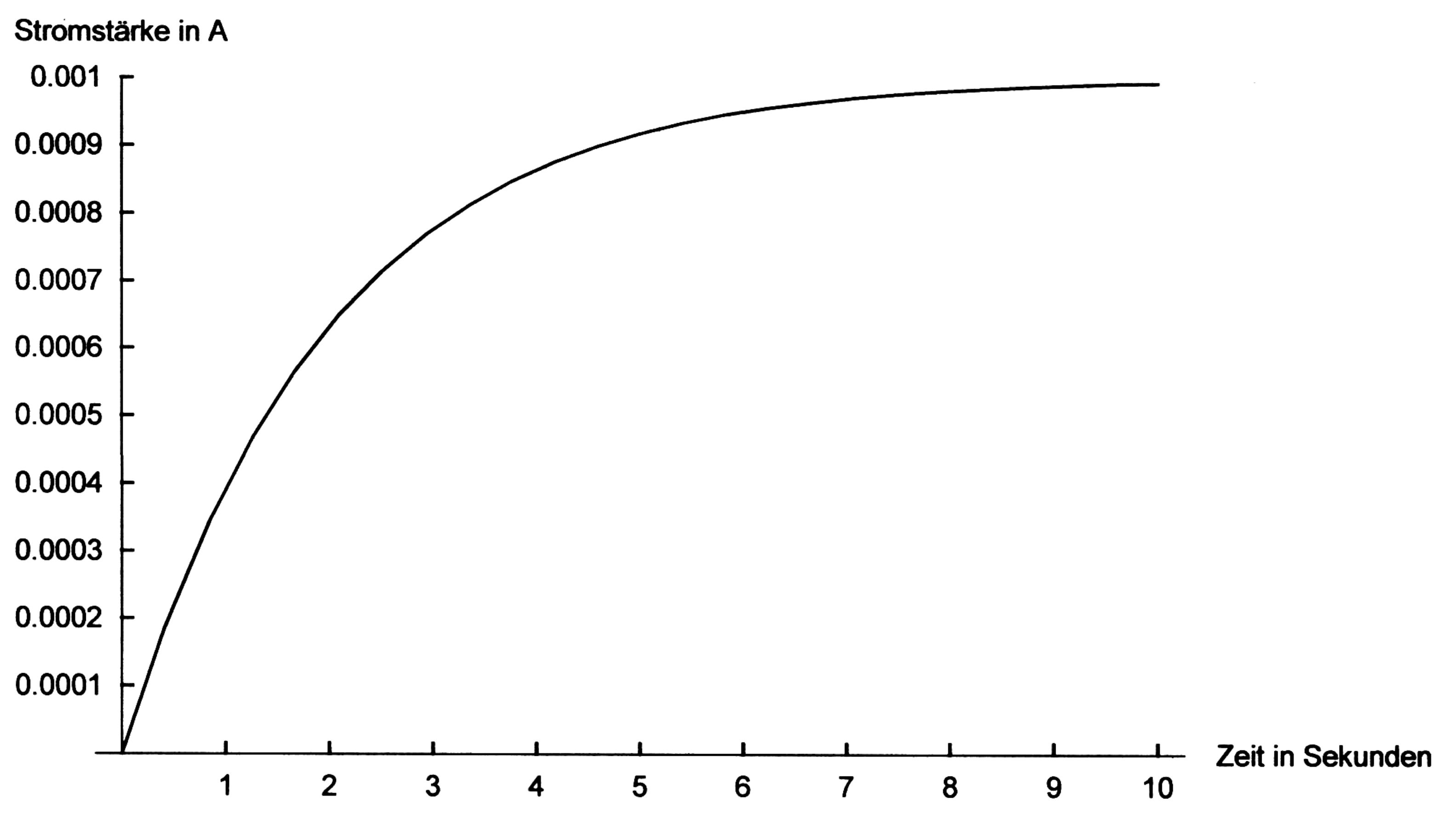
Falls man den Schalter schließt, ergibt sich folgender Stromstärke-verlauf.

a.) Beschreiben und erläutern Sie das Diagramm.

Erklären Sie dabei, wie es zu diesem Stromstärkeverlauf kommt.

b.) Bestimmen Sie mittels des Diagramms den Widerstand der Spule.

c.) Wie groß ist die momentane Spannung zum Zeitpunkt t = 2 s ?

Welche Induktionsspannung ergibt sich daraus zu diesem Zeit-

punkt? Erläutern Sie ihr Vorgehen. ( Kontrolle: U_ind = - 3,7 V )

d.) Bestimmen Sie die Induktivität der Spule aus dem Diagramm

( t = 2 s ). ( Kontrolle: L = 20.000 H ).

e.) Welche Permeabilität µ_r weist die 20 cm lange Spule auf, wenn sie

20000 Windungen hat und eine kreisförmige Querschnittsfläche

mit r = 5 cm. (mit Einheiten rechnen)

f.) Zeigen Sie anhand von 3 Wertepaaren, dass für die Stromstärke-

funktion die Gleichung I(t) = 0,001 A ∙ (1 − e^{− 0,5 ∙ t )} gilt.

Lösung:

a.) Beschreibung: Zunächst steigt die Stromstärke stark an. Dann

nimmt der Anstieg immer mehr ab und die Kurve flacht ab. Am Schluss

stabilisiert sich die Stromstärke auf einem maximalen Wert von

0,001 A. Es liegt eine Sättigungskurve vor.

Erklärung: Beim Schließen des Schalters beginnt der Stromfluss. Da-

durch baut sich ein Magnetfeld innerhalb der Spule auf. Diese Änder-

ung des Magnetfeldes führt nach dem Induktionsgesetz 2. Teil zu einer

Induktionsspannung. Diese Spannung ist nach der Lenzschen Regel

der anliegenden Spannung entgegengesetzt ausgerichtet. Sie behin-

dert also den Anstieg der insgesamt anliegenden Spannung, so dass

die Stromstärke nur allmählich zunimmt.

b.) Der Ohmsche Widerstand ergibt sich aus dem Ohmschen Gesetz.

Bei der Maximalstromstärke von 0,001 A liegt die Maximalspannung

von 10 V an. Es gilt somit

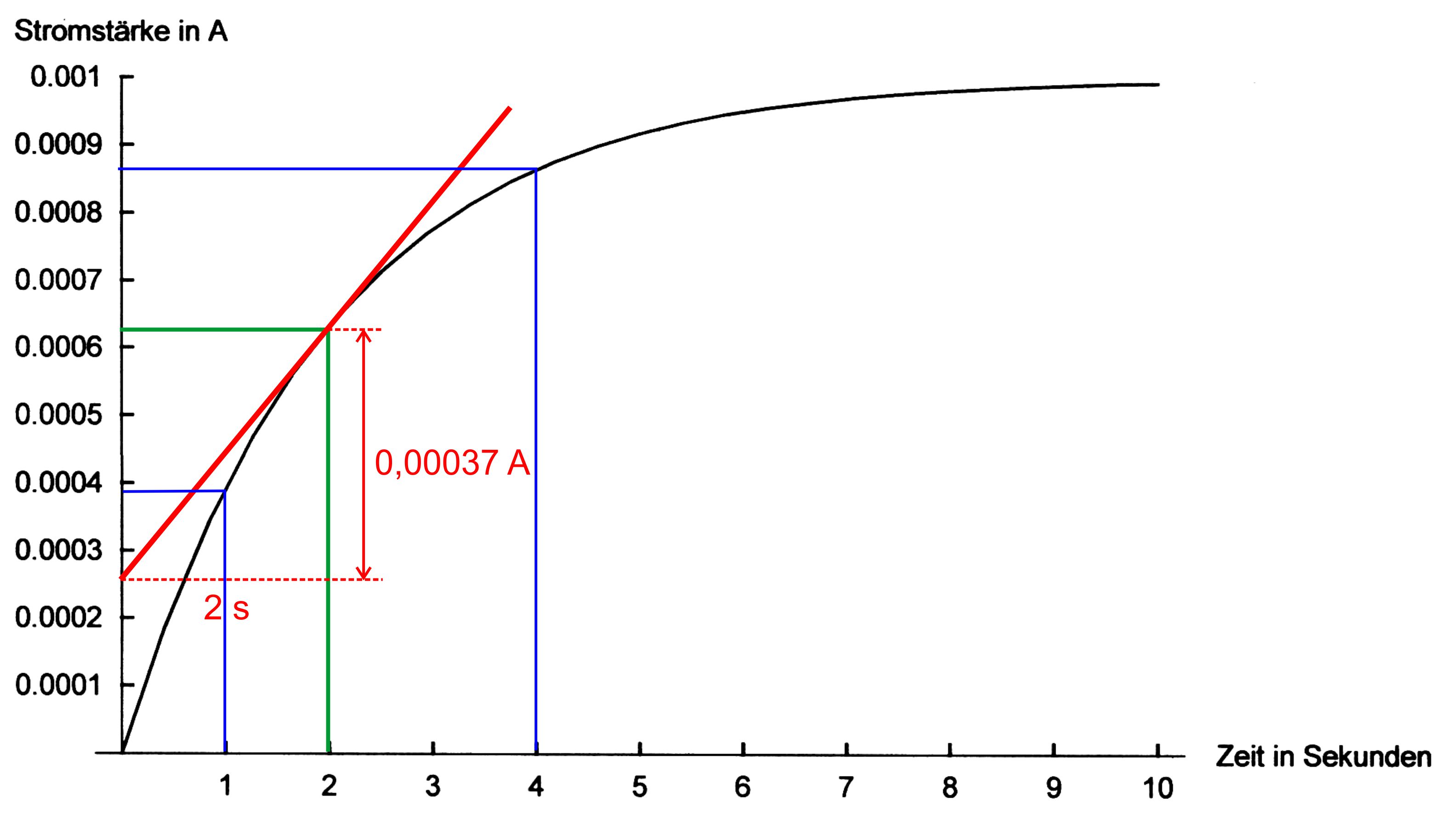
für c.), d.) und f.) wird folgende Zeichnung benutzt:

c.) Man liest zunächst die Stromstärke bei t = 2 s ab (s.grün).

Es ergibt sich I(2s) = 0,00063 A. Mit R = 10 kΩ aus b.) ergibt sich

hieraus die momentane Spannung U(2s) = R ∙ I = 10 kΩ ∙ 0,00063 A

= 6,3 V. Da ja gilt: U_momentan = U(t) = U₀ + U_ind ergibt sich für

U_ind = U(t) – U₀ = 6,3 V – 10 V = − 3,7 V.

d.) Für die Induktivität L braucht man die Steigung des Graphen an

der Stelle t = 2 s, da gilt U_ind = − L ∙ I‘(t) also

e.)

f.)

Wir lesen einfach die Werte für I (1 s, 2 s, 4 s ) am Diagramm ab und

vergleichen mit den berechneten Werten:

t = 1 s → I ( 1 s ) = 0,00039 A passt gut mit dem ablesbaren Wert

t = 2 s → I ( 2 s ) = 0,00063 A passt (s. c.))

t = 4 s → I ( 4 s ) = 0,00086 A passt ebenfalls

zurück zur Übersicht „Induktion“