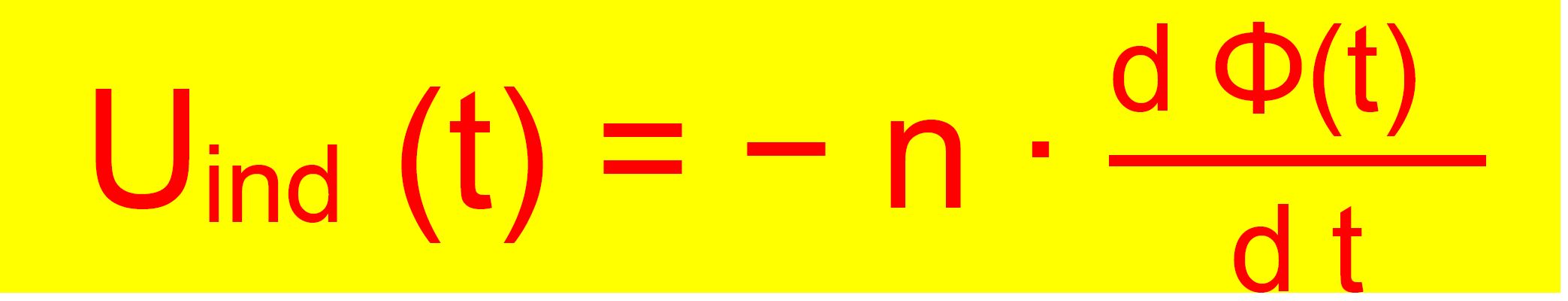gehe zu:

 

Induktionsgesetz−Zusammenfassung

 

Einführung

 

In den vorherigen Kapiteln haben wir uns mit zwei Möglichkeiten be-

schäftigt, eine Induktionsspannung zu erzeugen:

- einmal durch Bewegung, wobei innerhalb einer Spule die von Mag-

netfeldlinien durchsetzte Fläche geändert wird

- anderseits durch die Änderung der magnetischen Feldstärke inner-

halb einer Spule.

 

Man spricht in diesen Fällen vom Induktionsgesetz 1. bzw. 2. Teil.

 

Wir fassen noch einmal zusammen:

                                                                                                              

Induktionsgesetz 1. Teil

 

 

Induktion durch Flächenänderung

 

Ändert sich die von Magnetfeldlinien senkrecht durch-

setzte Fläche AꞱ , bestimmt sich die Induktionsspannung

über die Formel

 

 

mit

n = Windungsanzahl der Spule

B = magnetische Feldstärke

 

 

Induktionsgesetz 2. Teil

 

 

Induktion durch Änderung der Magnetfeldstärke

 

Für die Induktionsspannung ohne Bewegung gilt

die Formel

mit

n = Windungszahl der Induktionsspule

AꞱ = Fläche der Induktionsspule, die senkrecht von Feldlinien durch-

        setzt wird

dB(t)/dt = momentane Änderungsrate von B(t) bzw. Ableitung nach t

 

In diesem Fall spielt also die Änderung der Magnet-

feldstärke „dB(t)/dt“ die entscheidenden Rolle.

 

 

Wir werden im Folgenden jetzt beide Teile zu dem Induktionsgesetz

zusammenfügen.

 

Addition der Spannungen

 

Bisher haben wir ja beide Teile getrennt betrachtet. Welche Situation

ergibt sich aber, wenn beides gleichzeitig zutreffen, d.h. wenn während

einer Flächenänderung gleichzeitig eine Magnetfeldänderung stattfin-

det? Es liegen dann zwei Spannungen vor, die sich zu einer Gesamt-

spannung addieren.

 

Es gilt also:

 

 

Bei der Induktionsspannung geht es also um das Produkt aus

B(t) mit AꞱ(t). Dieses Produkt bekommt einen eigenen Namen und

wird magnetischer Fluss Φ(t) genannt.

 

 

Definition: Magnetischer Fluss Φ

 

Unter dem magnetischen Fluss versteht man

das Produkt aus AꞱ und B, d.h. es gilt

 

 

  Φ(t) = B(t) ∙ AꞱ(t)    

mit

B(t) = magnetische Feldstärke

AꞱ(t) = senkrecht mit Magnetfeldlinien durchsetzte Fläche

 

Einheit: [ Φ(t) ] = 1 V s = 1 Weber = 1 Wb

 

 

Das allgemeine Induktionsgesetz lautet somit:

 

Induktionsgesetz (allgemein)

 

 

Ändert sich innerhalb einer Spule mit n Windungen der

magnetische Fluss Φ, gilt für die Induktionsspannung

 

mit

n = Windungszahl

Φ(t) = B(t)∙AꞱ(t) = magnetischer Fluss

 

 

Anschauliche Vorstellung

 

Wenn man sich vorstellt, dass die magnetische Feldstärke anschau-

lich durch die Feldliniendichte , also „Anzahl der Feldlinien pro Fläche“,

dargestellt wird, kann man eine anschauliche Vorstellung vom mag-

netischen Fluss gewinnen.

 

Magnetischer Fluss = Magnetische Feldstärke ∙ Fläche =

Feldlinienanzahl/Fläche ∙ Fläche = Feldlinienanzahl

 

Eine anschauliche Formulierung des Induktionsgesetzes könnte also lauten

Induktionsgesetz (anschaulich)

 

 

Ändert sich innerhalb einer Spule mit n Windungen die

Anzahl der magnetischen Feldlinien, tritt innerhalb der Spule eine Induktionsspannung auf.

 

 

  gehe zu:

 

 

zurück zum Kapitel:

 

 

weiter zum Kapitel:

 

 

zurück zur Übersicht „Induktion“