Klausuraufgaben

Aufgabe Nr. 1 (LK-Niveau)

Eine große zylindrische Spule (Feldspule) wird an einen Sinusgenera-

tor angeschlossen. Der Sinusgenerator erzeugt einen sinusförmigen

Strom einstellbarer Frequenz. In die große Spule wird eine kleine

zylindrische Spule (Messspule) eingeschoben, so dass die Quer-

schnittsflächen beider Spulen parallel zueinanderliegen. Die kleine

Spule ist mit einem empfindlichen Voltmeter verbunden.

a.) Begründe ausführlich, warum man bei diesem Aufbau eine Span-

nung in der kleinen Spule messen kann.

b.) Man will herausfinden, wie die Spannung der kleinen Spule von

den Größen I_eff, f und d abhängt.

Es gilt dabei:

I_eff = effektive Stromstärke in der Feldspule

f = Frequenz der Sinusspannung in der Feldspule

d = Durchmesser der kleinen Spule

Es werden hierzu drei Versuche durchgeführt, deren Messergebnisse

unten aufgeführt sind. Werten sie diese Messergebnisse graphisch

aus. Am Schluss soll eine Gleichung stehen, mit der sich die Span-

nung U_eff der kleinen Spule in Abhängigkeit von den vorgegebenen

Größen ( I_eff,f und d) bestimmen lässt. [U_eff = effektive Spannung in

der kleinen Spule]

c.) Leiten Sie zum Schluss theoretisch eine Gleichung her, die einen

Zusammenhang zwischen den vorgegebenen Größen und der Span-

nung der Messspule herstellt.

Hinweis: Mathematisch muss man die „Kettenregel“ für Ableitungen kennen

1. Messreihe (f = 1000 Hz, d = 41 mm)

Ueff [mV]	5,7	8,7	11,8	14,2	16,7	19,4
Ieff [mA]	4	6	8	10	12	14

2. Messreihe (I = 10 mA, d = 41 mm)

Ueff [mV]	7,1	14,1	21,4	28,4	36,2	42,5
f [Hz]	500	1000	1500	2000	2500	3000

3. Messreihe (I = 10 mA, f = 1000 Hz)

Ueff [mV]	14,2	9,1	5,5
d [mm]	41	33	26

Lösung:

a.) Es gilt das Induktionsgesetz 2.Teil. Innerhalb der Messspule ändert

sich laufend die magnetische Feldstärke B(t), da diese von I(t) der

Feldspule linear abhängt. Bei Änderung der magnetischen Feldstärke

tritt aber nach dem Induktionsgesetz eine Induktionsspannung in der

kleinen Spule auf.

b.) Graphische Auswertung mit Hilfe von Excel:

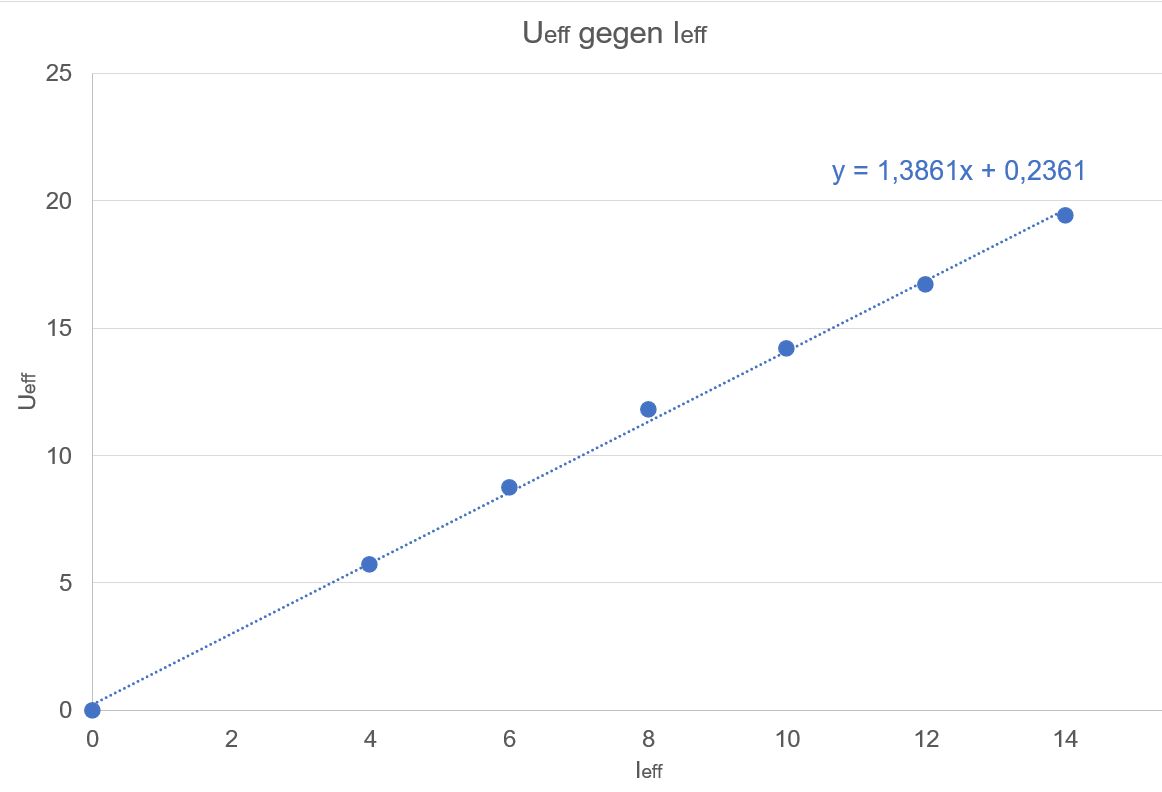
1. Fall: U_ind gegen I_eff aufgetragen

Ergebnis: Es liegt eine Ursprungsgerade vor, d.h. U_eff ~ I_eff

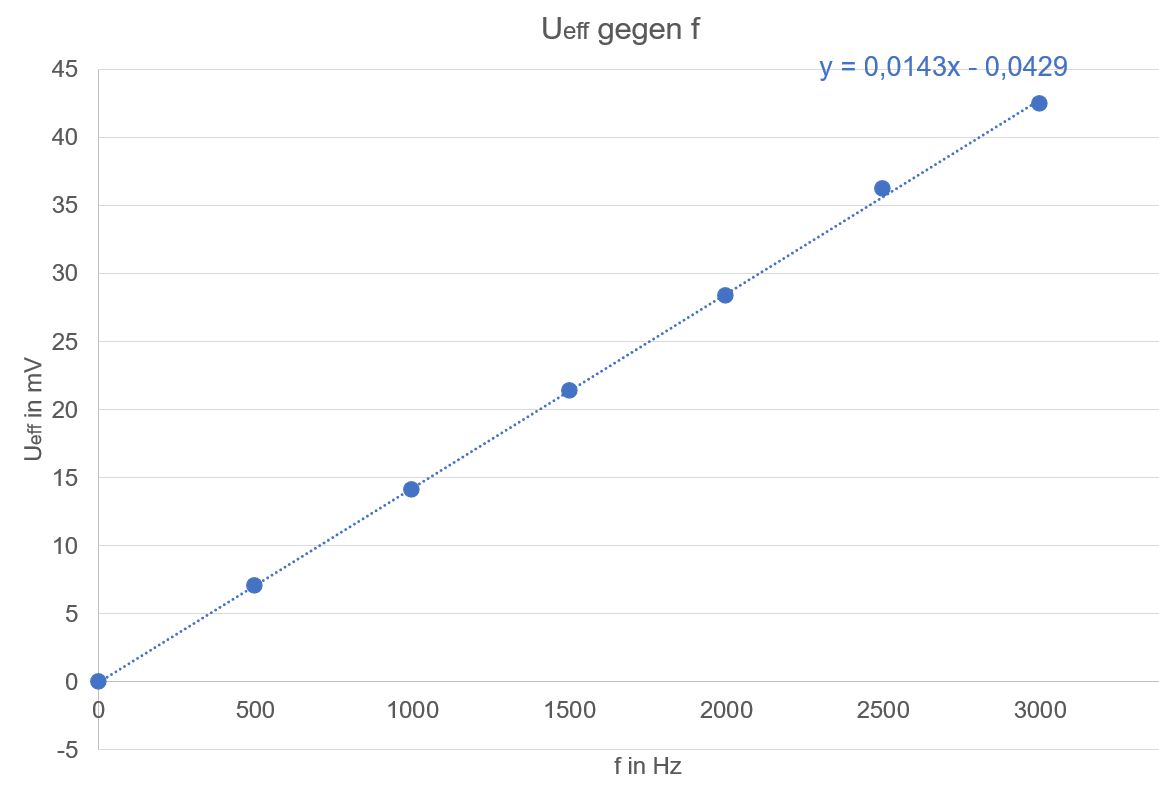
2. Fall: U_eff gegen f aufgetragen

Ergebnis: Auch hier liegt eine Ursprungsgerade vor, d.h. . U_eff ~ f

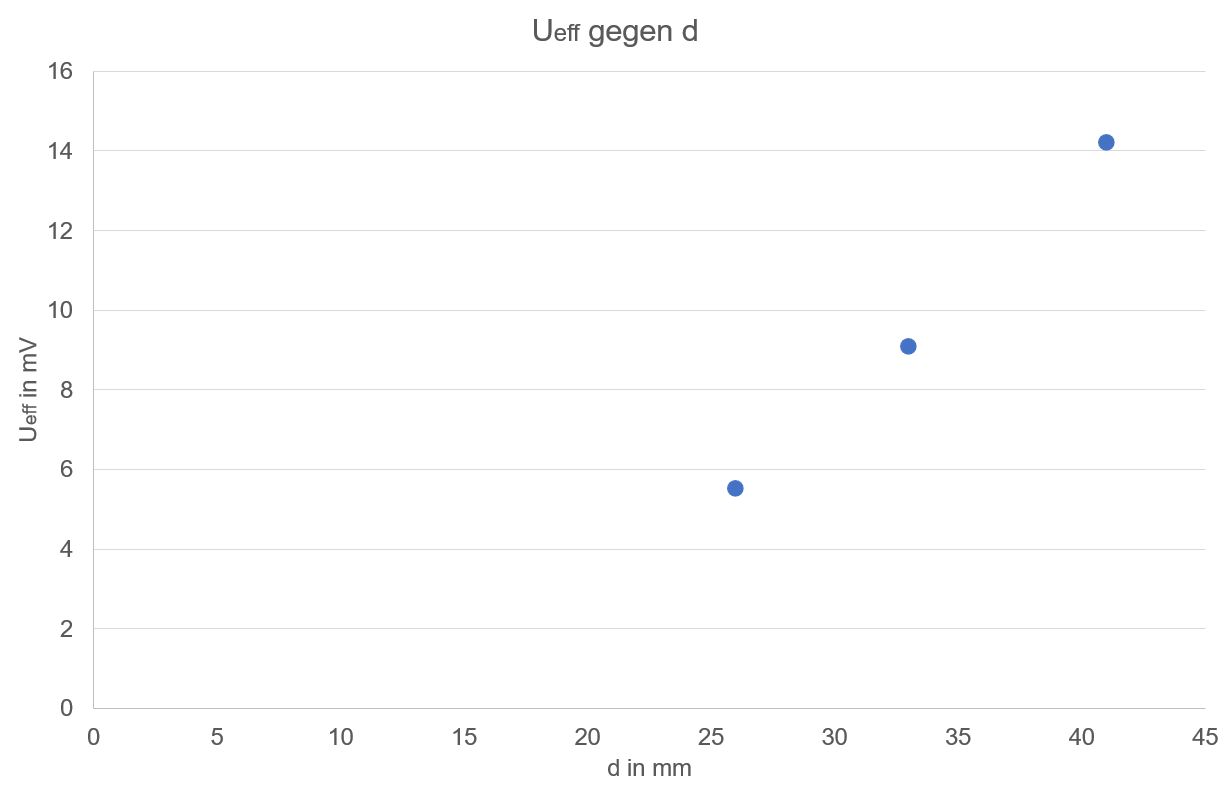
3.1. Fall: U_eff gegen d auftragen

Ergebnis: keine Ursprungsgerade → neuer Auftrag

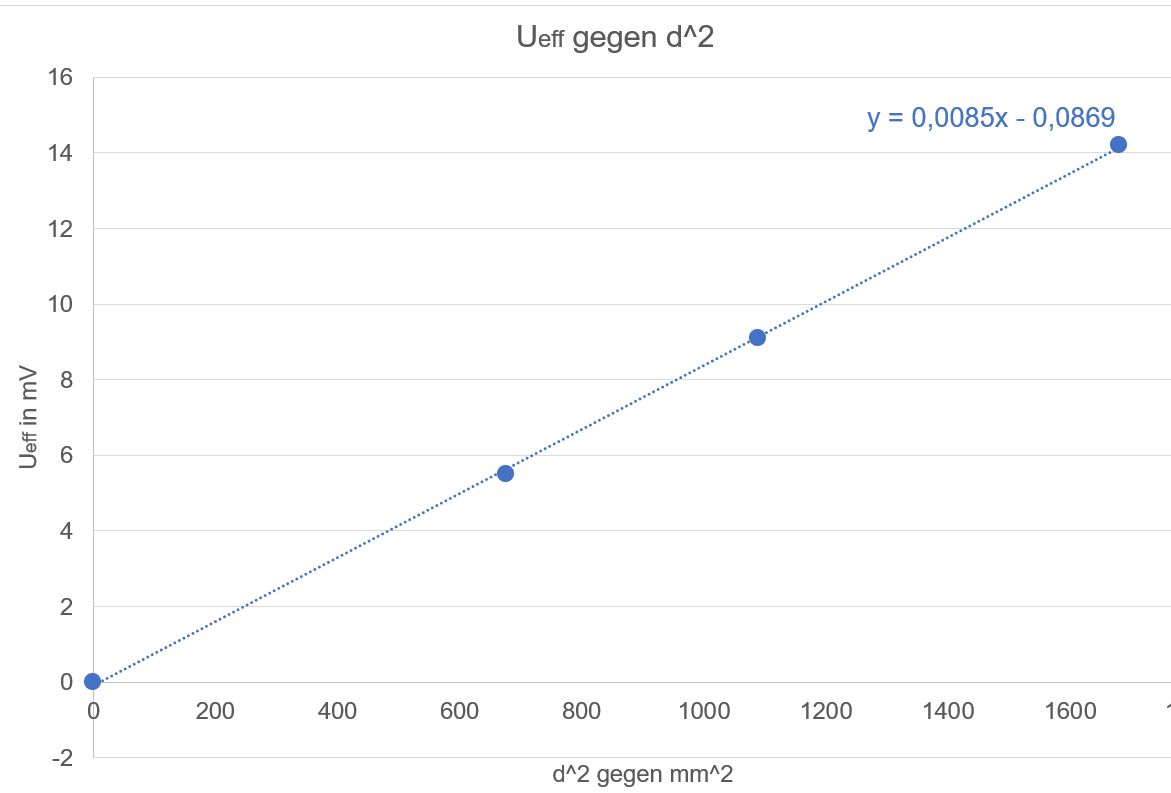
3.2. Fall: U_eff gegen d² aufgetragen

Ergebnis: Jetzt gibt es eine Ursprungsgerade, d.h. . U_eff ~ d²

Zusammenfassung:

U_eff ~ I_eff ; . U_eff ~ f _; U_eff ~ d² ergibt zusammen

U_eff ~ I_eff ∙ f ∙ d²

oder als Gleichung geschrieben

U_eff = k ∙ I_eff ∙ f ∙ d² ;

k = Proportionalitätskonstante

Bestimmung von k:

Wir wählen einfach konkrete Wertepaare:

U_eff = 14,2 mV; I_eff = 10 mA ; f = 1000 Hz, d =41 mm (1. Fall, 4. Wertepaar)

c.)

Exkurs: Gehen wir davon aus, dass die Versuche mit dem Phywe-

aufbau erfolgt sind, gilt n_ind = 300 und n_F = 485 Wdg./ m.

Hieraus ergibt sich für k:

Dies entspricht ungefähr dem experimentellen Wert.

zurück zum „Induktionsgesetz allgemein“

zurück zur Übersicht „Induktion“