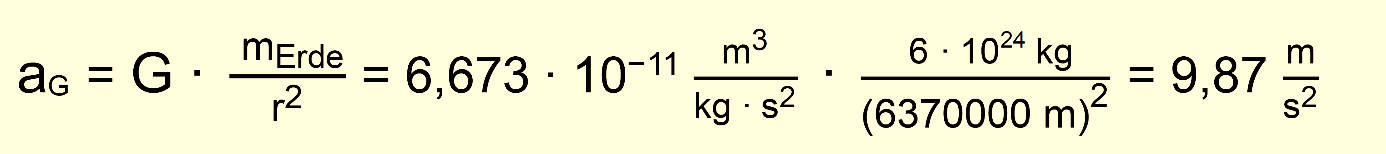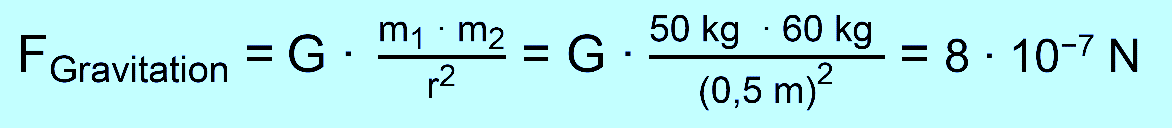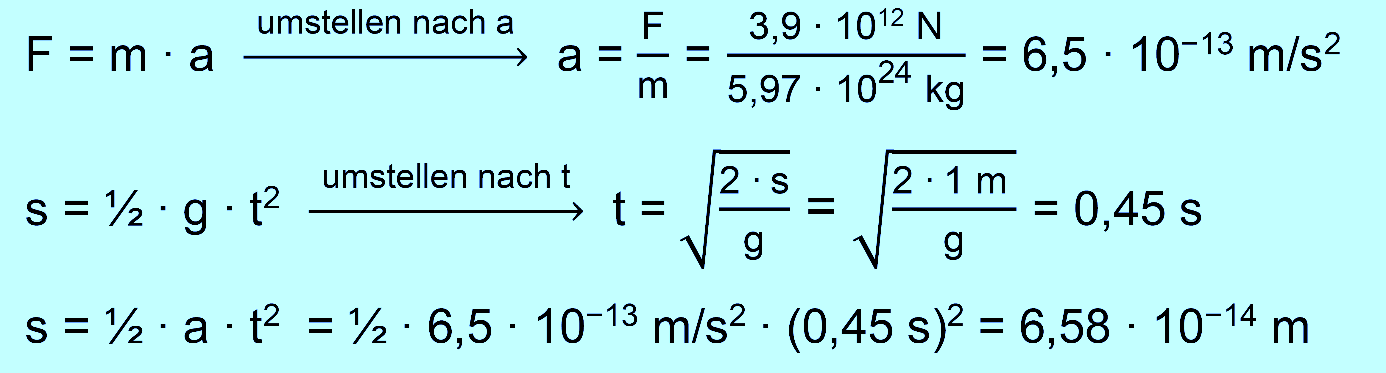|
Link zu: Gravitationsgesetz Herleitung des Gravitationsgesetzes Bevor
man dieses Kapitel bearbeitet, sollte man sich zunächst mit dem Kapitel
„Weltbilder“ beschäftigen, da aus diesem
Kapitel Inhalte zur Herleitung
benutzt werden. Vor allem das 3. Keplersche Gesetz wird zur
Herleitung benutzt werden. Außerdem machen wir eine Verein-fachung, da wir davon ausgehen, dass sich die Planeten
auf Kreis- bahnen
und nicht auf Ellipsen bewegen. Also
jetzt zur Herleitung. Uns interessiert
die Kraft, die dafür sorgt, dass die Planeten auf ihrer Kreisbahn
bleiben. Diese Kraft zeigt zum Kreismittelpunkt, also zur Sonne
und wird von dieser ausgeübt. Im Kapitel „Kreisbewegungen“ haben
wir diese Kraft als „Radialkraft“ kennengelernt. Man
geht von der Formel für die Radialkraft aus und setzt dort die Geschwindigkeitsformel
aus dem 3. Keplerschen Gesetz ein. Es gilt
also:
Wie man
erkennt, taucht nicht die Sonnenmasse auf, obwohl es klar sein
dürfte, dass diese Masse auch eine Rolle für die Kraft spielen dürfte.
Dies wird auch klar, wenn man weiß, dass nach dem 3. Axiom von Newton, der Planet auf die Sonne die gleiche Kraft ausübt
wie die
Sonne auf den Planeten. Also vom Planeten aus betrachtet in der Formel
statt der Planetenmasse die Sonnenmasse stehen würde. Die Sonnenmasse
ist in der Konstanten C1 versteckt, so dass man end- gültig
für die Kraftbeziehung zwischen Planeten und Sonne findet:
Die
Gravitationskonstante lässt sich experimentell bestimmen. Hierzu muss
aber noch etwas ausgeholt werden (s. unten). Bemerkenswert
ist, dass in dieser Formel keinerlei Bewegungsgrößen mehr
sind, sondern nur die Massen und die Entfernung der Massen- schwerpunkte. Was
kann man jetzt mit diesem Gesetz anfangen? Es gilt ja zunächst nur für
die Bewegung von Körpern („Planeten“) um einen sehr masse- reiches
Zentralkörper, da es aus dem 3. Keplerschen Gesetz herge- leitet
wurde. Bestimmung der Masse des
Zentralkörpers Wir können jetzt die Massen von Sonne und Erde bestimmen. Wie geht das genau? Man hat zwei Möglichkeiten die Kraft der Sonne auf einen
Planeten zu bestimmen, nämlich über die neue Gravitations- formel
oder/und über die Formel für die Radialkraft. Im Folgenden sehen
wir den entsprechenden Ansatz und die Herleitung der Massen- formel:
Verallgemeinerung des
Gravitationsgesetzes Bisher
gilt das Gravitationsgesetz nur für die Bewegung von Körpern um ein
massereiches Zentrum. Das Verdienst von Newton war es, dass er
dieses Gesetz sehr viel allgemeiner formuliert hat. Um zu
dieser Verallgemeinerung zu kommen, schauen wir uns einmal die
Bewegung des Mondes um die Erde an. Es soll
um die Radialbeschleunigung gehen, mit der der Mond von der Erde angezogen
wird. Wir berechnen diese zunächst mit der Radial- oder
Gravitationskraft mit Hilfe des 2. Axiom von
Newton.
Jetzt
rücken wir einmal den Mond näher an die Erde heran bis er als Massepunkt
auf der Erdoberfläche sich befindet. Die Rechnung ergibt dann:
Bei der
Einsetzung ganz exakter Zahlen für die Erdmasse kommt man auf
einen Wert von 9,81 m/s2. Dies ist ein Wert, der also genau der
Fallbeschleunigung „g“ entspricht. Dies
bedeutet, dass die Kraft, die für die Bewegung der Planeten (hier den
Mond) zuständig ist, auch der Kraft entspricht, die die Massen auf der Erde
anzieht. Wir
können also verallgemeinern, dass die Gravitationskraft eine Kraft
ist, die nicht nur in der Astronomie eine große Rolle spielt, sondern
vielmehr überall, wo Massen sich gegenseitig anziehen. Die
Verallgemeinerung des Gravitationsgesetzes lautet also:
Zusatzmaterial - Erneute Bestimmung der Erdmasse Im
Kapitel „Verallgemeinerung des Gravitationsgesetzes“ haben
wir gesehen,
dass man die Anziehungskraft der Erde auf eine Masse auf der
Erdoberfläche über zwei Formeln bestimmen kann. Einmal
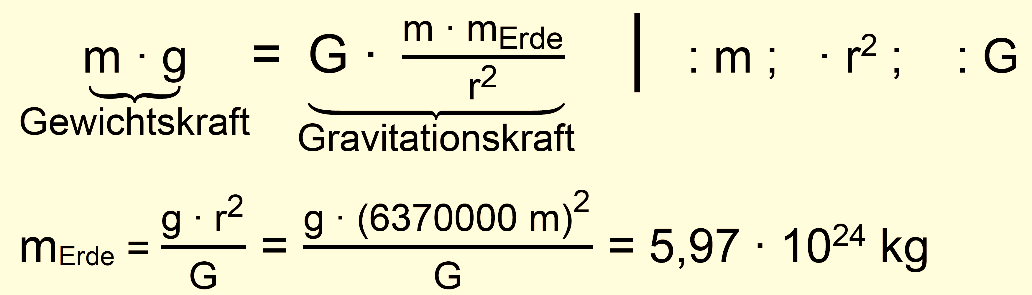
über die Gewichtskraft und dann über die Gravitationskraft. Es gilt
also:
Dieser
Wert ist besser als der im Kapitel „Weltbilder“ ermittelte Wert. Dies
liegt daran, dass die Bewegung des Mondes und der Erde um
einen gemeinsamen Schwerpunkt erfolgt (s.unten).
„g“
sollte natürlich möglichst exakt gemessen werden. Dies ist z.B. über
die Schwingungsdauer
eines Fadenpendels möglich. - Bestimmung der Gravitationskonstanten Hinweis zum Anfang: Wir erklären das Verfahren nicht im Detail, da dies z.Z.
nicht mehr zum Themenbereich der E-Phase gehört. Würde die Gravitation noch einmal in einem
LK-Physik vorkommen, müsste man hierauf genauer eingehen. Ich stelle hier am Ende
Unterlagen zur Verfügung, mit denen man sich dann detaillierter in das Thema
einarbeiten kann. Man bekommt einen sehr guten Überblick durch das Video von
Prof. Rene Matzdorf. Zur
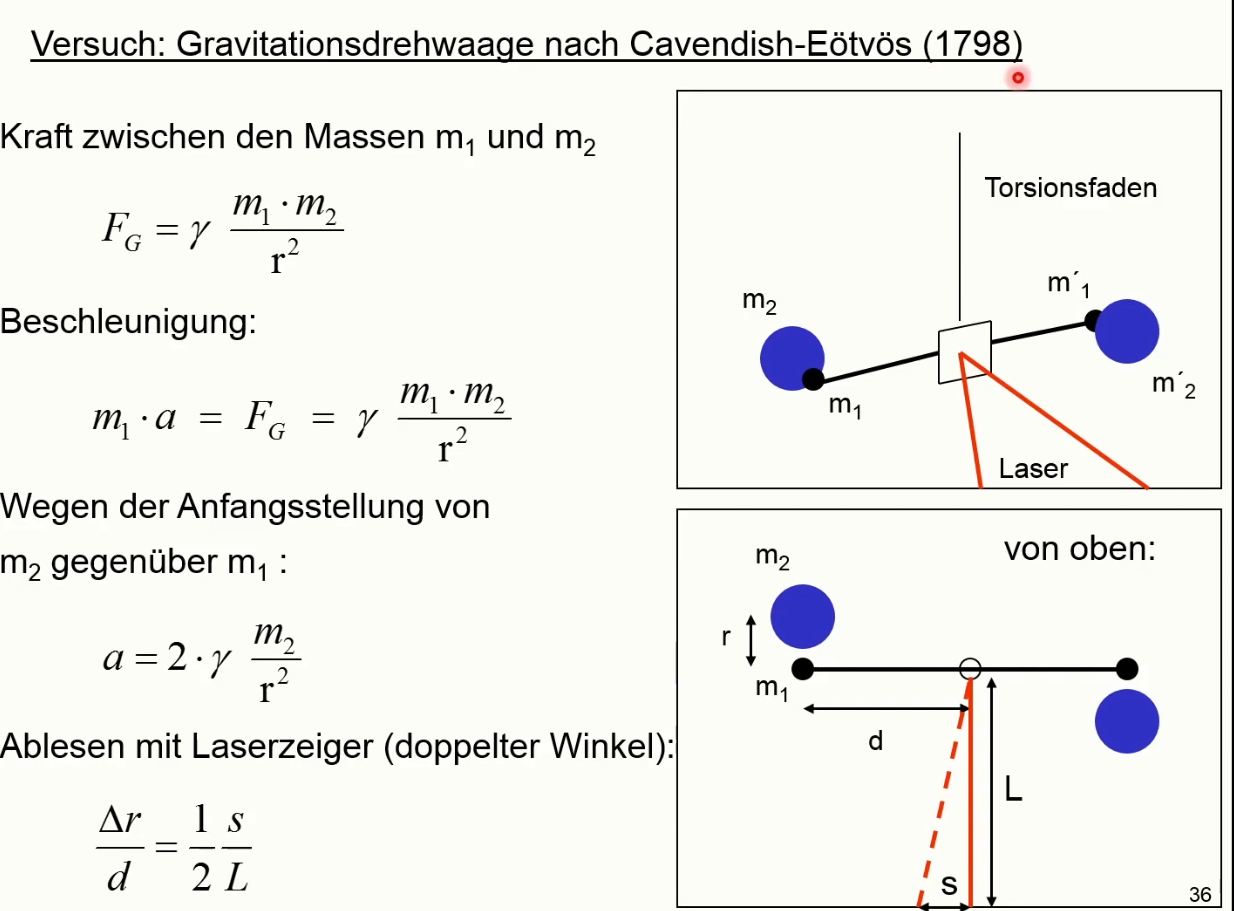
Messung der Gravitationskonstanten wird eine Drehwaage be- nutzt,
auf der sich paarweise eine kleine und große Masse gegenüber stehen.
Der ganze Aufbau befindet sich an einem Faden, der sich verdrillen kann. Auf
diesem Faden ist ein Spiegel angebracht, auf den ein
Laserstrahl fällt, dessen Reflexion in größerer Entfernung auf einer Skala
betrachtet wird. Die
großen Massen werden einen Tag vor der Messung in die Nähe der
kleinen Massen gebracht. Der Faden verdrillt sich dann aufgrund der
Gravitationswirkung zwischen den Massen und kommt zur Ruhe. Am
nächsten Tag werden die großen Massen umgeschwenkt und stehen jetzt jeweils
der anderen kleinen Masse gegenüber. Hierdurch tritt
wieder eine Gravitationskraft auf und den Faden verdrillt sich in die
andere Richtung. Diese Verdrillung wird mit dem Laserstrahl an die
Wand projiziert und führt zu einer beschleunigten Bewegung des Laserstrahls.
Diese Beschleunigung wird gemessen und damit die Gravitationskonstante
bestimmt. Wenn man die Bewegung des Laser- punktes
länger verfolgt, merkt man dass der Faden eine
gedämpfte Schwingung ausführt bis er seine Endlage erreicht. Für unsere Be- schleunigungsmessung wird nur die erste Phase dieser gedämpften Schwingung
betrachtet. Es muss
mit äußerster Vorsicht gearbeitet werden. Jede Erschütte- rung
muss vermieden werden (schon ein vorbeifahrender LKW kann Einfluss
nehmen). Link-Liste zum Thema
-
Bewegung um einen gemeinsamen Schwerpunkt Bisher
haben wir immer so getan, als ob sich bei den Bewegungen eines
„Planeten“ um seinen Zentralkörper der Mittelpunkt der Bewe- gung
dem Mittelpunkt des Zentralkörpers entspricht. Bei
genauerer Betrachtung stimmt dies nicht, sondern beide Körper bewegen
sich um einen gemeinsamen Schwerpunkt. Einfaches
Beispiel dazu: Zwei Schüler stehen sich gegenüber und fassen
sich an den Armen. Dann bewegen sie sich umeinander. Es wird nie möglich
sein, dass einer der Schüler an einem festen Dreh- ort
bleibt, sondern sie bewegen sich um einen Punkt, der zwischen ihnen
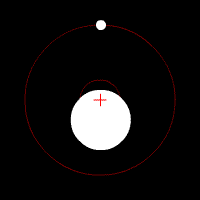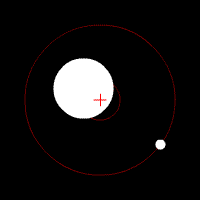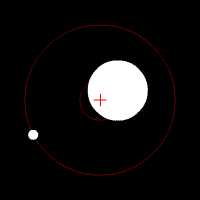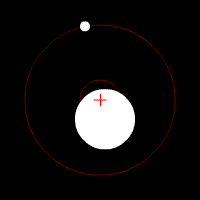
liegt, ihren gemeinsamen Schwerpunkt. Für das
System Erde-Mond gibt es hier eine schöne Animation bei Wikipedia:
Quelle: https://de.wikipedia.org/wiki/Erde-Mond-Schwerpunkt Wenn man
das System genauer untersucht, kommt man zu einer Art „Hebelgesetz“
für dieses System. Es gilt
nämlich:
mE
∙ rE−S = mM ∙ rM−S ; mit mE und
mM = Massen der Körper
rE−S und rM−S =
Abstände zum Schwerpunkt Dies
bedeutet, dass der Schwerpunkt immer näher am massereicher-en Körper liegt,
z.B. beim System Erde-Mond noch innerhalb der Erde. - Gezeiten Die Gezeiten lassen sich nur vollständig erklären, wenn man von der Drehung um einen gemeinsamen
Schwerpunkt ausgeht. Das folgende Video ist das einzige, das ich gefunden
habe, welches die Gezeiten physikalisch vollständig und korrekt erklärt. (Hinweis: das Video scheint es nicht mehr auf youtube zu
geben; deshalb kann ich keine Quellenangabe geben) Link zu: |