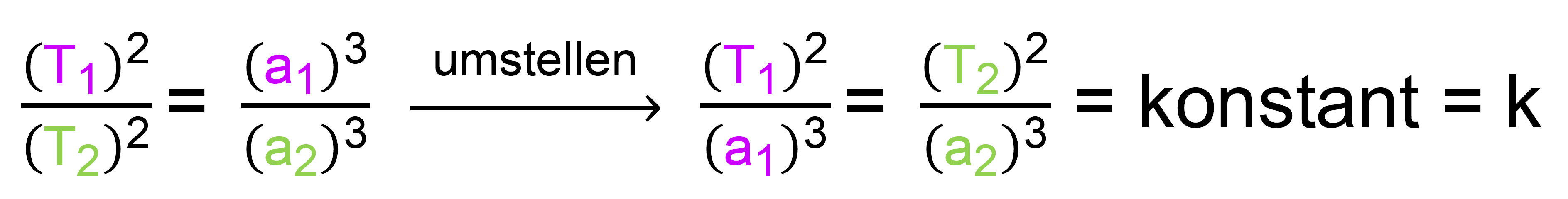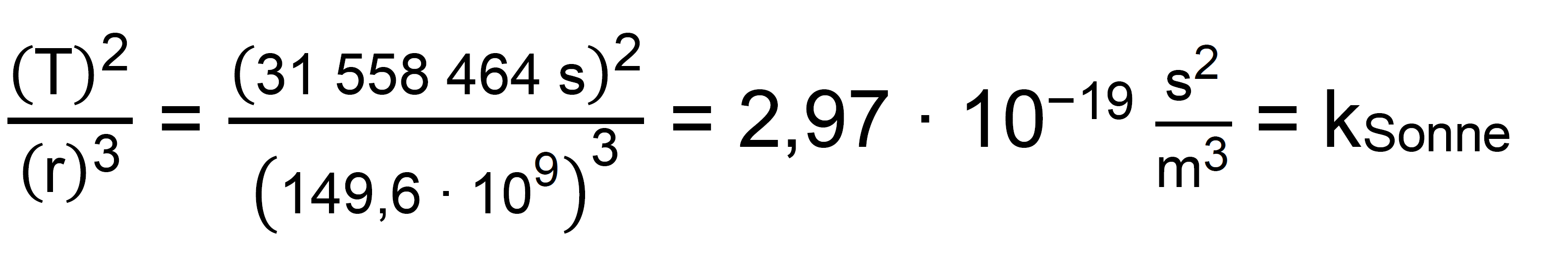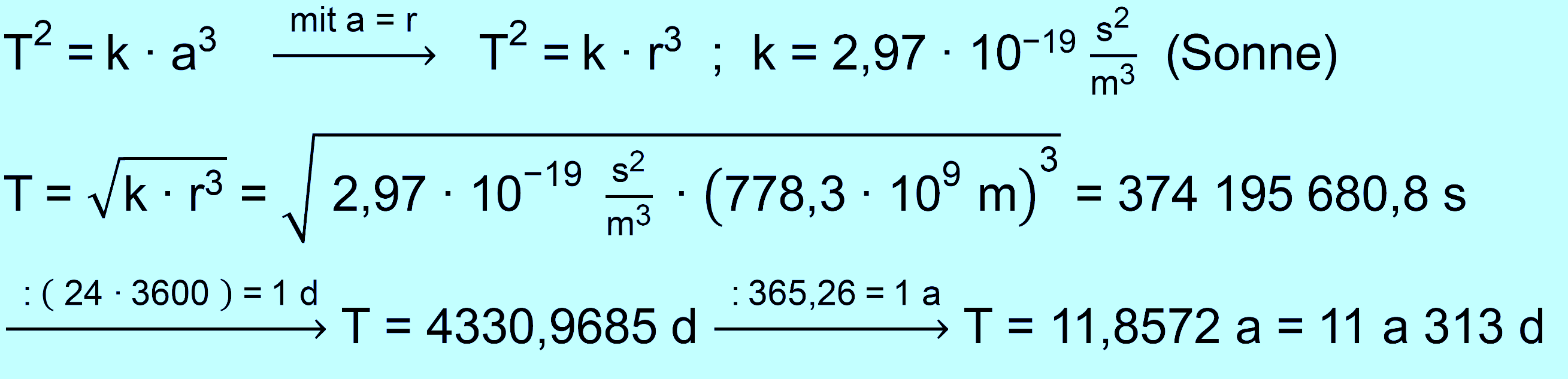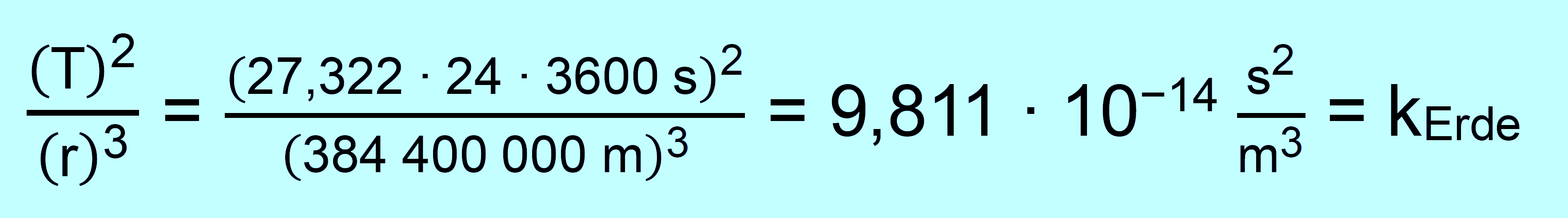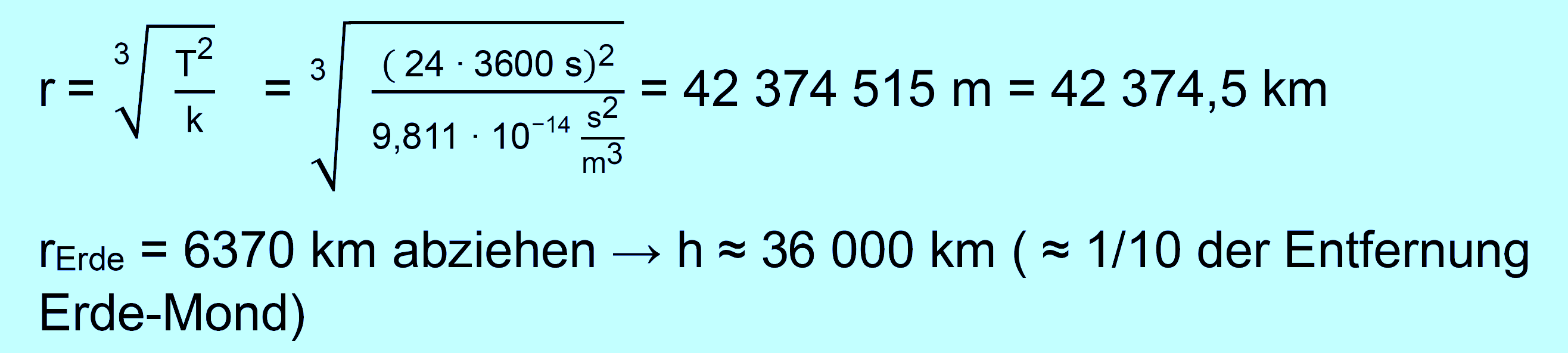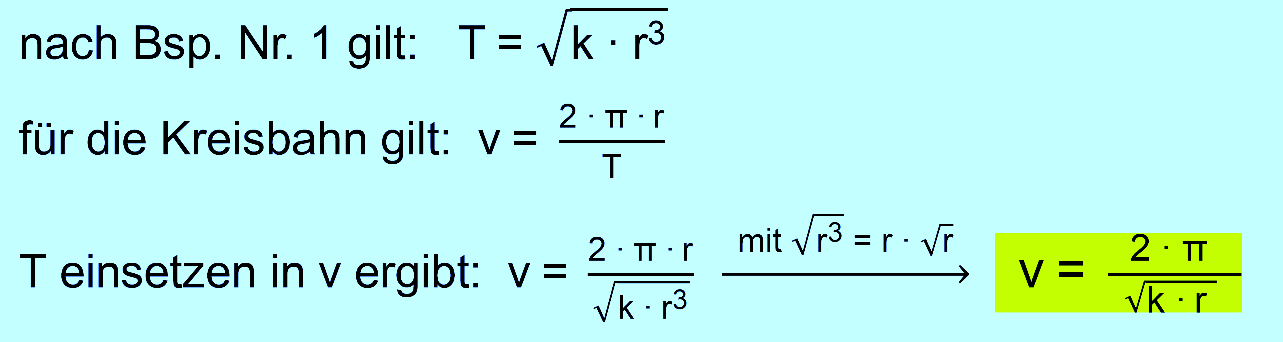|
Weltbilder Bevor wir uns mit dem eigentlichen
Gravitationsgesetz beschäftigen, wollen wir einen kurzen Ausflug in die
Geschichte der Astronomie machen und uns mit den verschiedenen Vorstellungen
vom Aufbau der Welt beschäftigen. Hinweis: der Ausflug
soll wirklich nur kurz sein. Alles wird sehr ausführlich in „wikipedia“ behandelt (s.
Verlinkungen bzw. Link-Liste)) Schwerpunkt werden die beiden
Weltbilder sein, die jahrhundertelang gegolten haben bzw. noch gelten. Es
geht um das geozentrische Welt- bild und das heliozentrische Weltbild. Verbunden sind
die jeweiligen Weltbilder mit den Namen von Ptolemäus
(100 − 160 n.Chr.) und Kopernikus (1473
− 1543 n.Chr.). Man erkennt schon an den Jahres- zahlen, dass zwischen den einzelnen
Weltbildern 1400 Jahre liegen. Die allmähliche Anerkennung des
heliozentrischen Weltbildes hat noch einmal 100 Jahre gedauert, wobei
sicherlich auch Kepler
(1571 − 1630 n.Chr.) seinen Beitrag geleistet
hat. Warum gehen wir kurz auf die
Weltbilder ein? Wir werden die Keplerschen Gesetzen dazu nutzen, das
Gravitationsgesetz herzu- leiten. Geozentrisches Weltbild Der Name sagt es schon, dass hier die
Erde den Mittelpunkt der Welt bildet, was ja zunächst mal
offensichtlich erscheint, weil sich alle Er- scheinungen am Himmel „anscheinend“ um die Erde drehen. Also gilt: Die Erde steht im Mittelpunkt. Alle anderen
Himmelskörper (Planeten, Sonne, Mond, Fixsterne) drehen sich um die
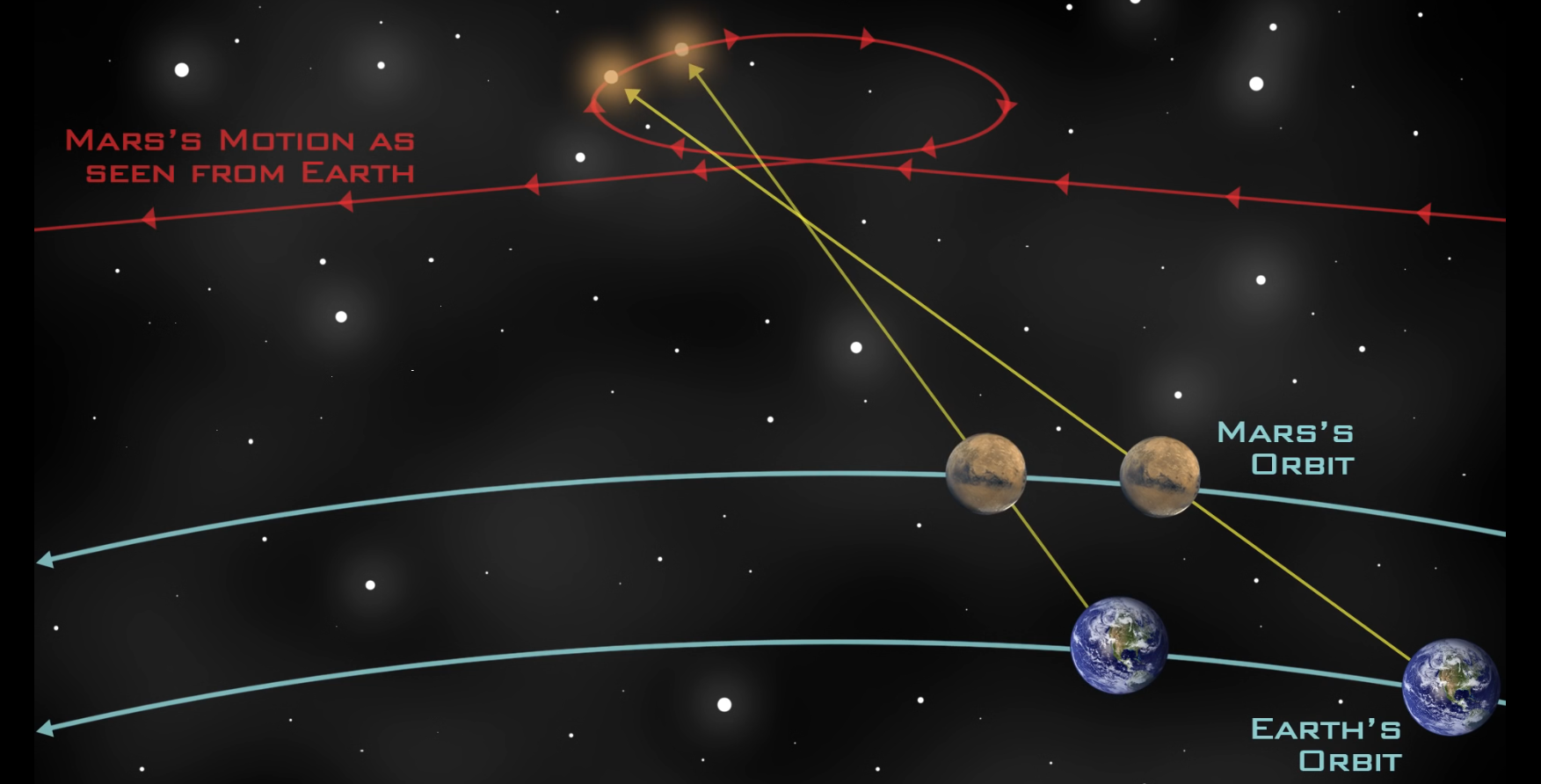
Erde. Probleme: 1.) Es gibt Rückwärtsbewegungen am Himmel
von Planeten, so- genannte Planentenschleifen.
Wie will man diese erklären? 2.) Man postulierte eine „gleichförmige Kreisbewegungen“
für die Planeten. Aristoteles (384 −
322 v.Chr.) hatte hierbei einen maßgeb- lichen Einfluss. Diese Probleme und weitere
Beobachtungen zu den Umlaufzeiten usw. führten dazu, dass man bei den
Planeten nicht
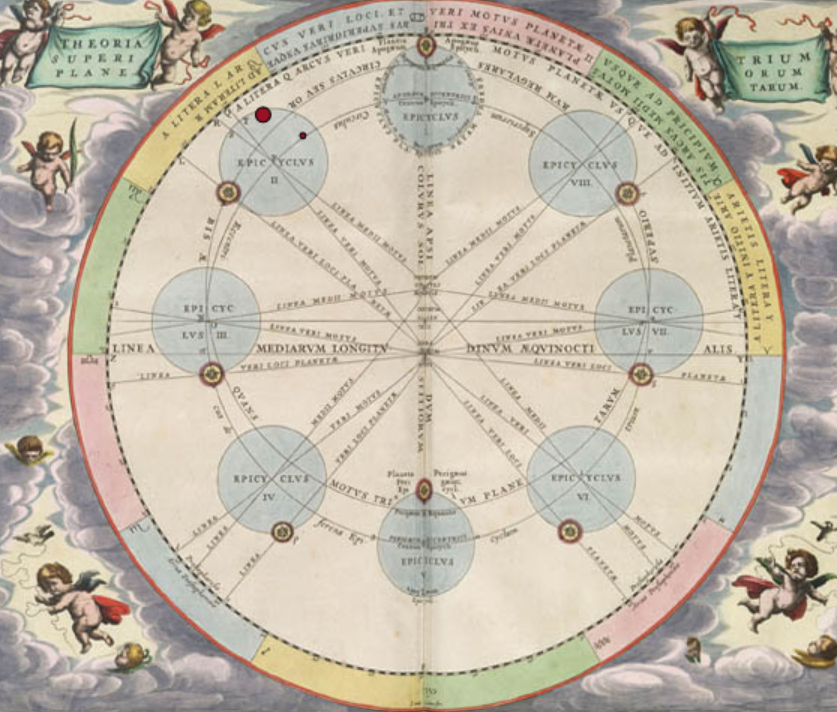
mit einer gleich- förmigen Kreisbewegung auskam. Man musste mehrere Kreisbewe- gungen miteinander kombinieren. Es entstand die Epizykeltheorie, bei der auf einem Kreis, dem Deferenten, ein weiterer kleiner Kreis (Epizykel) sich befand, auf dem sich der Planet bewegte, während sich der Mittelpunkt des Epizykels sich auf dem Deferenten bewegte. Der Mittelpunkt des Deferenten lag dabei nicht im Erdmittelpunkt. Um die gleichförmige Bewegung zu retten, musste sogar noch ein Ausgleichs- punkt, der Äquant; eingeführt werden. Dieser bezog sich auf den Mit- telpunkt des Epizykels. Es war alles äußerst kompliziert. Hierzu jetzt noch einige Links zu
Animationen und Abbildungen. Hinweis: die
Animationen und das Bild stammen aus der astrokramkiste, die die freundlicher- weise frei zur
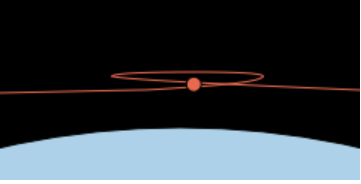
Verfügung stellt. Vielen Dank dafür. 1. Animation: Planetenschleife
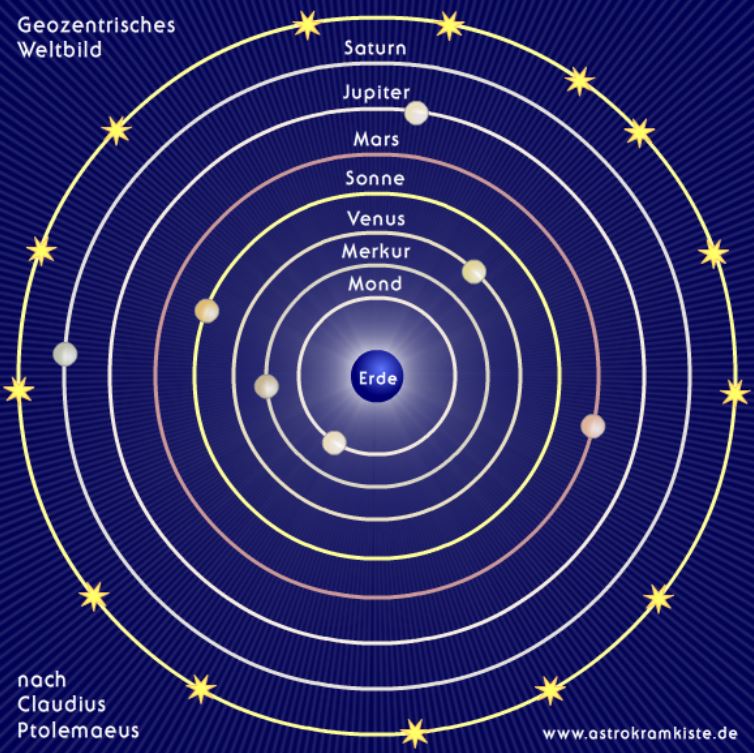
(Animation) 2. Geozentrisches Weltbild - noch ohne
Epizykel (Bild)
3.) Geozentrisches Weltbild (ohne
Epizykel) - Animation 4.) Geozentrisches Welt - Epizykel -
Animation Heliozentrisches
Weltbild (Kopernikus) Auch hier verrät natürlich der Name sofort, dass jetzt die Sonne im Mittelpunkt des Universums bildet und sich die Planeten um die Sonne drehen. Der Mond bekommt eine Sonderstellung, da er die Erde um- kreisen darf. Hier gilt also: Die Sonne steht im Mittelpunkt. Alle Planten,
also auch die Erde, drehen sich um die Sonne. Der Mond umkreist
die Erde. Weiterhin gibt es folgendes Problem: Man postulierte immer noch eine „gleichförmige Kreisbewegungen“
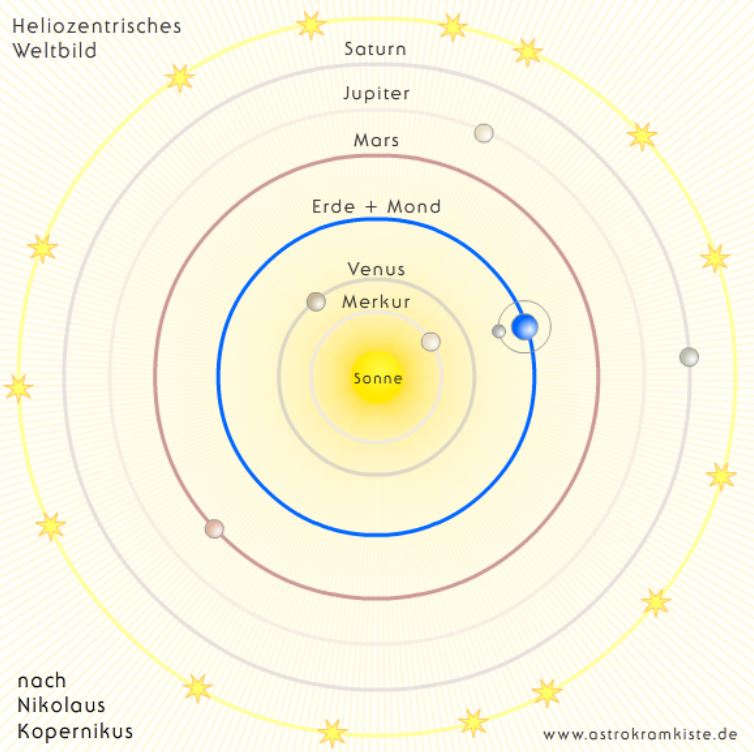
für die Planeten. Somit ist das Weltbild von Kopernikus nicht sehr viel einfacher als das von Ptolemäus, da es weiterhin reichlich Epizykel braucht, um die Bewegung der Planenten mit der damaligen Genauigkeit zu erklären. In der folgenden Abbildung fehlen die zahlreichen Epizykel. Es ist nur der grobe Aufbau erfasst. Hinweis: die Abbildung stammt wieder
aus der astrokramkiste. Ich suche noch eine
Abbildung für Kopernikus mit den Epizykeln (leider
bisher ergebnislos)
Ein großer Vorteil des neuen Weltbildes war, dass es die Planenten- schleifen deutlich einfacher erklären konnte. In folgendem Video wird dies sehr umfangreich erläutert (auch mit einem Rückblick auf die Erklärung im geozentrischen Weltbild). Quelle: https://www.youtube.com/watch?v=1nVSzzYCAYk Heliozentrisches Weltbild (Kepler) Kepler hatte sicherlich den Vorteil, dass ihm umfangreiche Messdaten von Tycho Brahe zur Verfügung standen, um sich ein eigenes Bild von der Bewegung der Planeten zu machen. Mit Hilfe der Daten ent- wickelte er die drei Keplersche Gesetze, die sicherlich auch mit zum Durchbruch zum heliozentrischen Weltbild verholfen haben. Diese drei Gesetze lauten: 1.
Gesetz: Die
Planenten bewegen sich auf Ellipsenbahnen, in deren einem Brennpunkt
die Sonne steht. 2.Gesetz: Der
Fahrstrahl, d.h. die Verbindungslinie zwischen Sonne und Planet,
überstreicht in gleichen Zeiten die gleiche Fläche. 3.Gesetz: Die
Quadrate der Umlaufzeiten T1 bzw. T2 zweier Planeten ver- halten
sich wie die dritten Potenzen ihrer großen Halbachse a1 bzw.
a2. Für unser weiteres Vorgehen, nämlich
die Herleitung des Gravitations- gesetzes, ist sicherlich das 3.Gesetz das Bedeutenste. Ein paar Erläuterungen zu den
Keplerschen Gesetzen sind sicherlich hilfreich. Zunächst sollte man ein
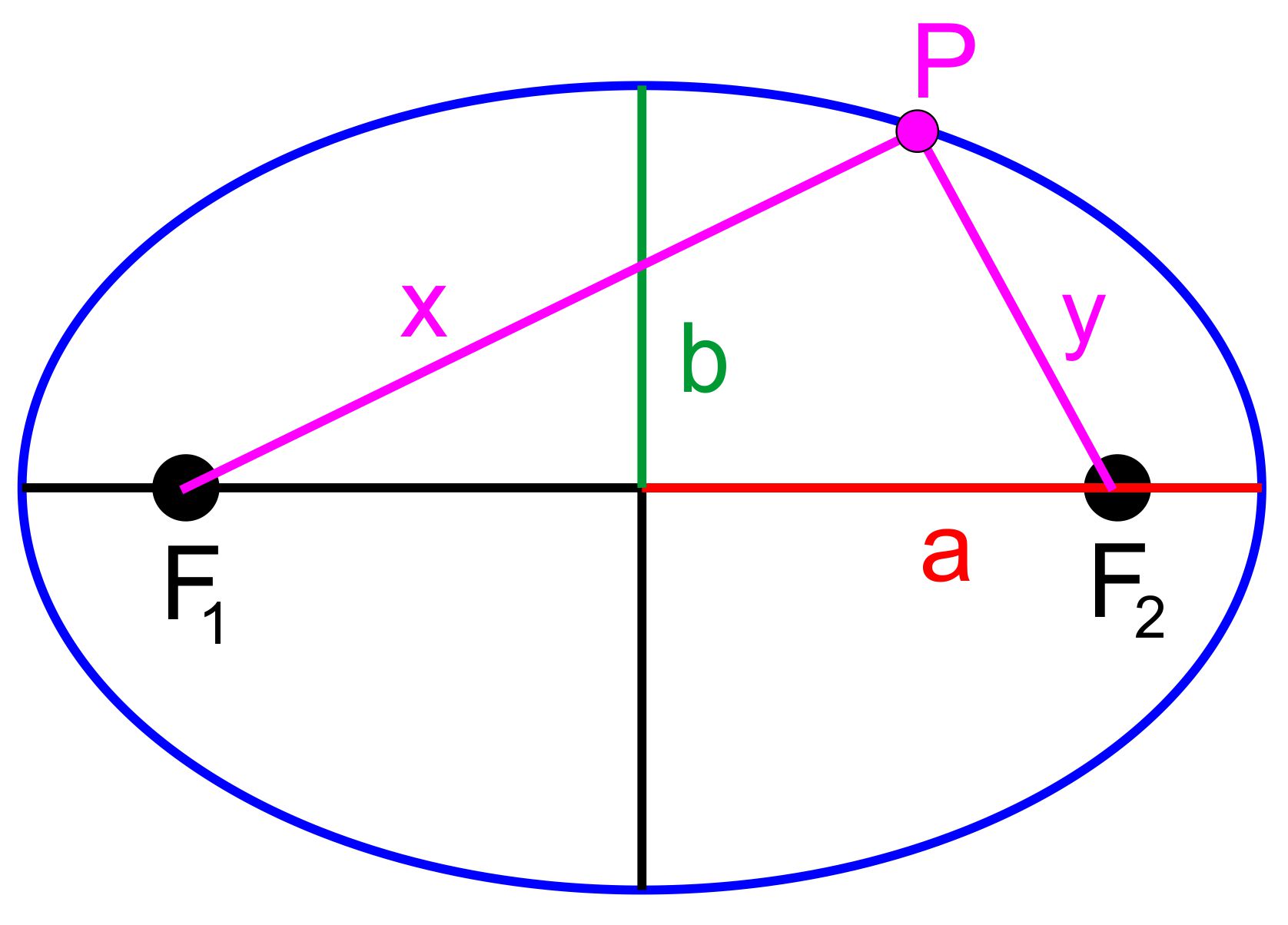
paar Kenntnisse zur Ellipse haben. In der folgenden Abbildung sehen wir
mal eine Ellipse:
Für die Benennungen
gilt: a = große Halbachse (größte Länge vom Mittelpunkt bis zum
Rand) b = kleine Halbachse (kleinste Länge vom Mittelpunkt bis
zum Rand) F = Brennpunkte x,y = Abstand zwischen einem Punkt auf der Ellipse zu den
Brennpunkten Eine wichtige Eigenschaft einer Ellipse ist, dass für alle Punkte auf der Ellipse die Gleichung x + y = 2 ∙ a gilt.
Dies nutzt man bei der Gärtnerkonstruktion
einer Ellipse aus. In wikipedia
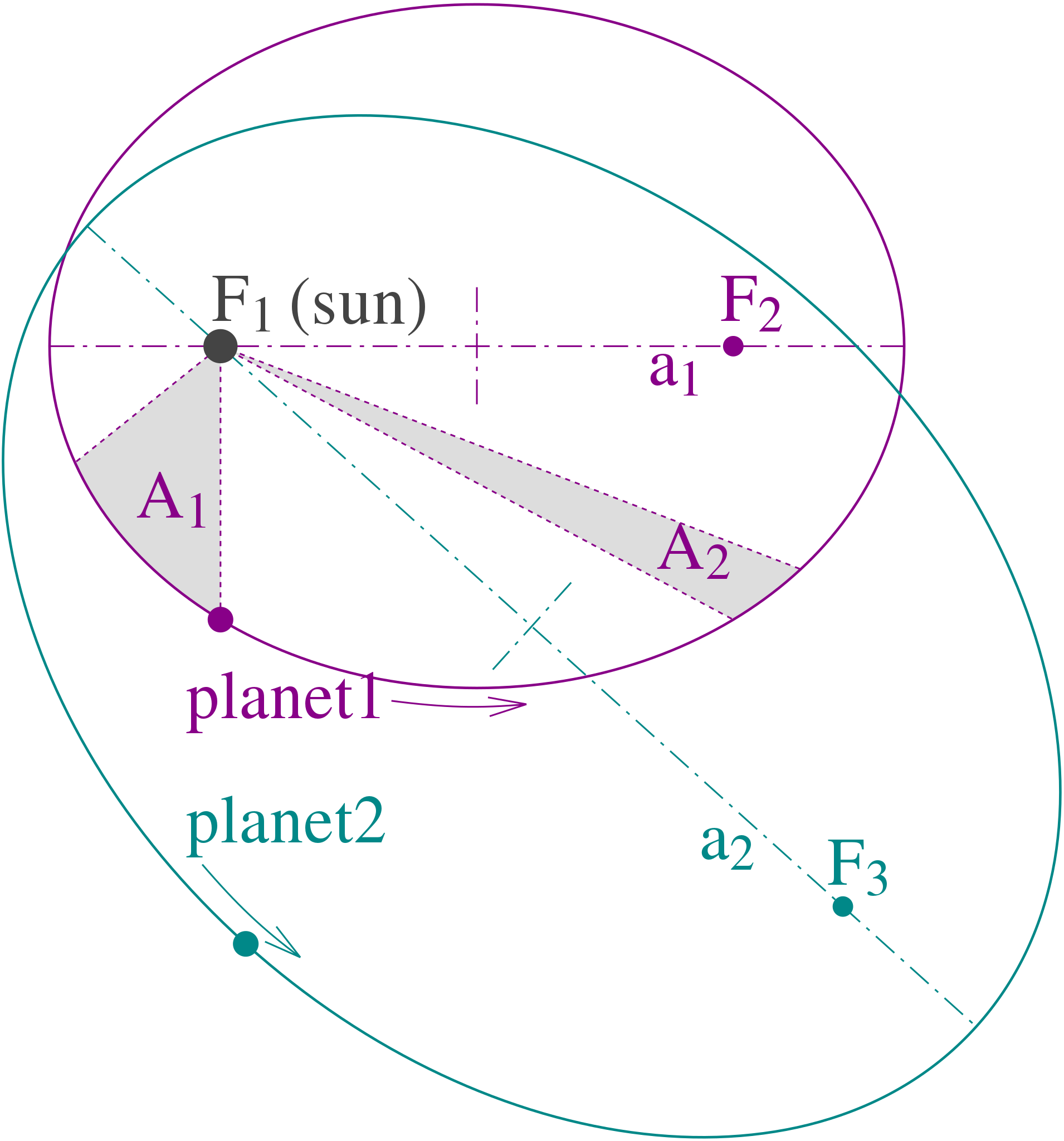
gibt es eine schöne Abbildung, mit der sich alle drei Gesetze schön erklären lassen.
Quelle: https://de.wikipedia.org/wiki/Keplersche_Gesetze Erläuterung: 1.) Die „violette“ und die „grüne“
Bahn sind zwei Ellipsen, auf denen sich zwei verschiedene Planeten
bewegen. Beide haben als gemein- samen Brennpunkt die Sonne. 2.) Beim violetten Planeten findet man
grauen Flächen A1 und A2. Dies sind zwei Flächen gleicher Größe. Die gestrichelte Linie ist der Fahrstrahl, der jeweils die gleiche Zeit zurückgelegt haben soll. Wichtig: Da gilt A1 = A2 muss der Planet in der Nähe des Brenn- punktes (also der Sonne) sich schneller bewegen als in größerer Entfernung, denn die Strecken auf der Bahnkurve sind für die gleiche Zeit unterschiedlich lang (s. Defintion der Geschwindigkeit). Kepler
macht hier den entscheidenden Schritt weg von der gleich- förmigen
Bewegung, die ja seit Aristoteles postuliert wurde! 3.) Für uns am wichtigsten ist, dass es einen Zusammenhang zwischen den Umlaufdauer T1 und
T2 und
den großen Halbachsen a1 und a2 gibt. Wichtig: Als Gleichung geschrieben gilt:
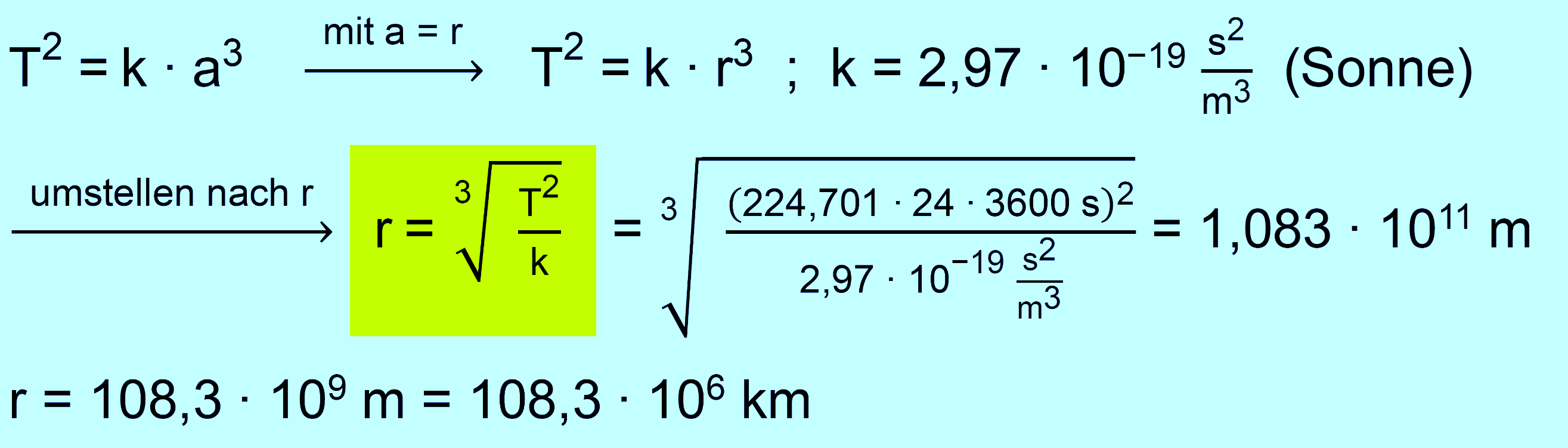
Was bedeutet dies? Die Umlaufdauer und die Entfernung zur Sonne sind nicht frei wählbar, sondern sie sind über die Konstante k mitein- ander verbunden. Die Konstante wird Keplerkonstante genannt. Diese Beziehung zwischen der Umlaufdauer T und der Halbachse a besteht für alle Systeme, bei denen Körper sich um einen massereichen Zentralkörper bewegen. k hat aber je nach System einen anderen Wert und muss für jedes System neu bestimmt werden. Man benötigt dafür aber nur die Umlaufdauer T eines Planeten und die Länge der großen Halb- achse diese Planeten. Da man praktisch fast immer davon ausgeht, dass die Ellipse nahezu ein Kreis ist, reicht die Entfernung zum Zentralkörper aus.
Beispiel:
Bestimmung der Keplerkonstante für unser Sonnensystem In unserem Sonnensystem kennen wir am besten unseren eigenen Planeten, die Erde. Hierfür gilt: T = 365,26 d = 365,26 ∙ 24 ∙ 3600 s = 31 558 464 s a = r = 149,6 ∙ 106 km = 149,6 ∙ 109 m
Geschwindigkeitsformel (Kepler) Aus dem 3. Keplerschen Gesetz lässt sich unter der Annahme einer Kreisbahn auch eine Formel für die Planentengeschwindigkeit gewinnen, die uns bei der Herleitung des Gravitationsgesetzes noch von Nutzen sein wird. Es gilt:
Man erkennt, dass die
Bahngeschwindigkeit vom Bahnradius r ab- hängt. Je geringer der Abstand des
Planeten zur Sonne ist, um so schneller muss er sich um die Sonne
bewegen.
|