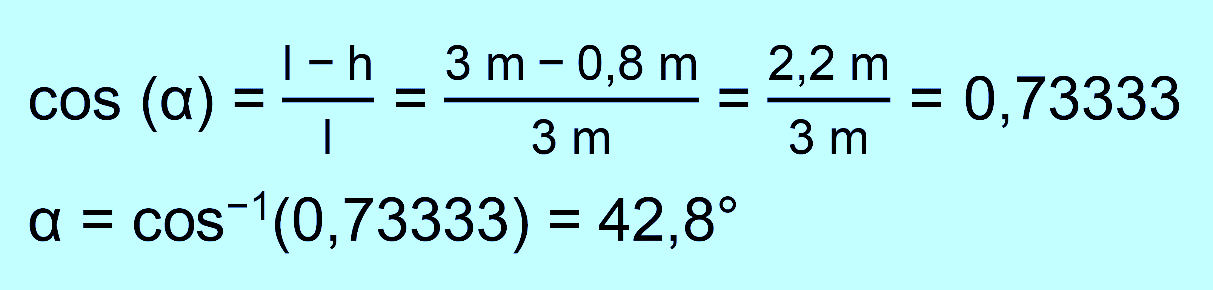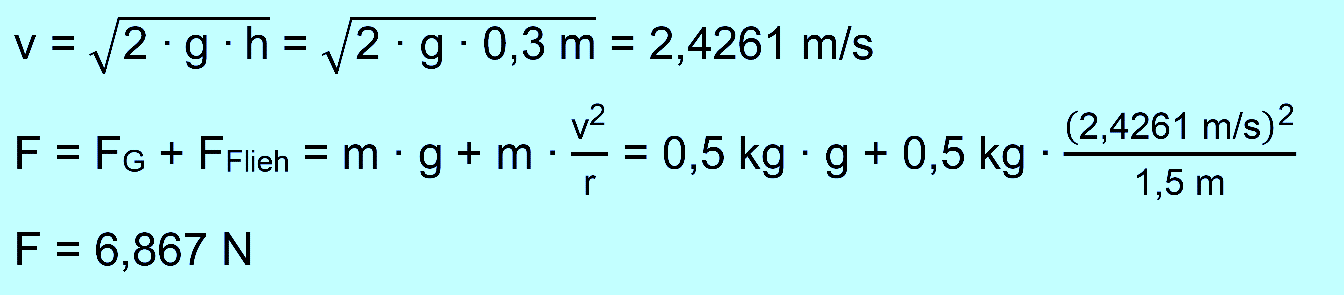|
- zur
Aufgabe Nr.1 - zur Aufgabe Nr.2 - zur
Aufgabe Nr.3 Komplexaufgaben Hinweis:
Bei diesen Aufgaben werden viele Themenbereich ange-sprochen.
Man muss praktisch fast alle Inhalte bearbeitet haben. 1.
Aufgabe: (Schraubenfeder,
Energieerhaltung, Impulsformeln, schiefe
Ebene)
Ein Wagen
Nr.1 mit der Masse 2 t wird über einen Lifthill 60
m hoch gezogen.
Oben wird der Wagen durch ein Katapult zusätzlich be- schleunigt.
Dieses Katapult besteht aus einer Extremschraubenfeder mit einer
Federkonstanten D = 10 000 N/kg, die 2 m zusammenge- drückt wurde.
Der Wagen wird von der gespannten Feder beschleunigt bis sich
die Feder vollständig entspannt hat (s.
Federpistole). Danach bewegt sich der Wagen nach unten und stößt dort
elastisch auf einen Wagen Nr.
2 mit einer Masse von 3 t. Dieser zweite Wagen kann da- nach eine schiefe Ebene hinauffahren. Welche
maximale Höhe erreichen die beiden Wagen jeweils nach dem Stoß? Lösung: Man muss zunächst die Geschwindigkeit am Boden bestimmen. Hierzu benutzt man den Energieerhaltungssatz. Es muss daher zunächst die Energie am Anfang berechnet werden. Diese setzt sich aus Spannenergie und potentieller Energie zusammen.
Am Boden ist dann die Startenergie vollständig in Bewegungsenergie umgewandelt worden. Man gewinnt die Geschwindigkeit vor dem Stoß.
Mit Hilfe der Impulsformeln kann man dann die Geschwindigkeiten nach dem Stoß bestimmen.
Wenn die kinetische Energie nach dem Stoß vollständig in potentielle Energie umgeformt wurde, liegt die maximale Höhe vor.
2.
Aufgabe: (Energieerhaltung, schiefer
Wurf, Trigonometrie)
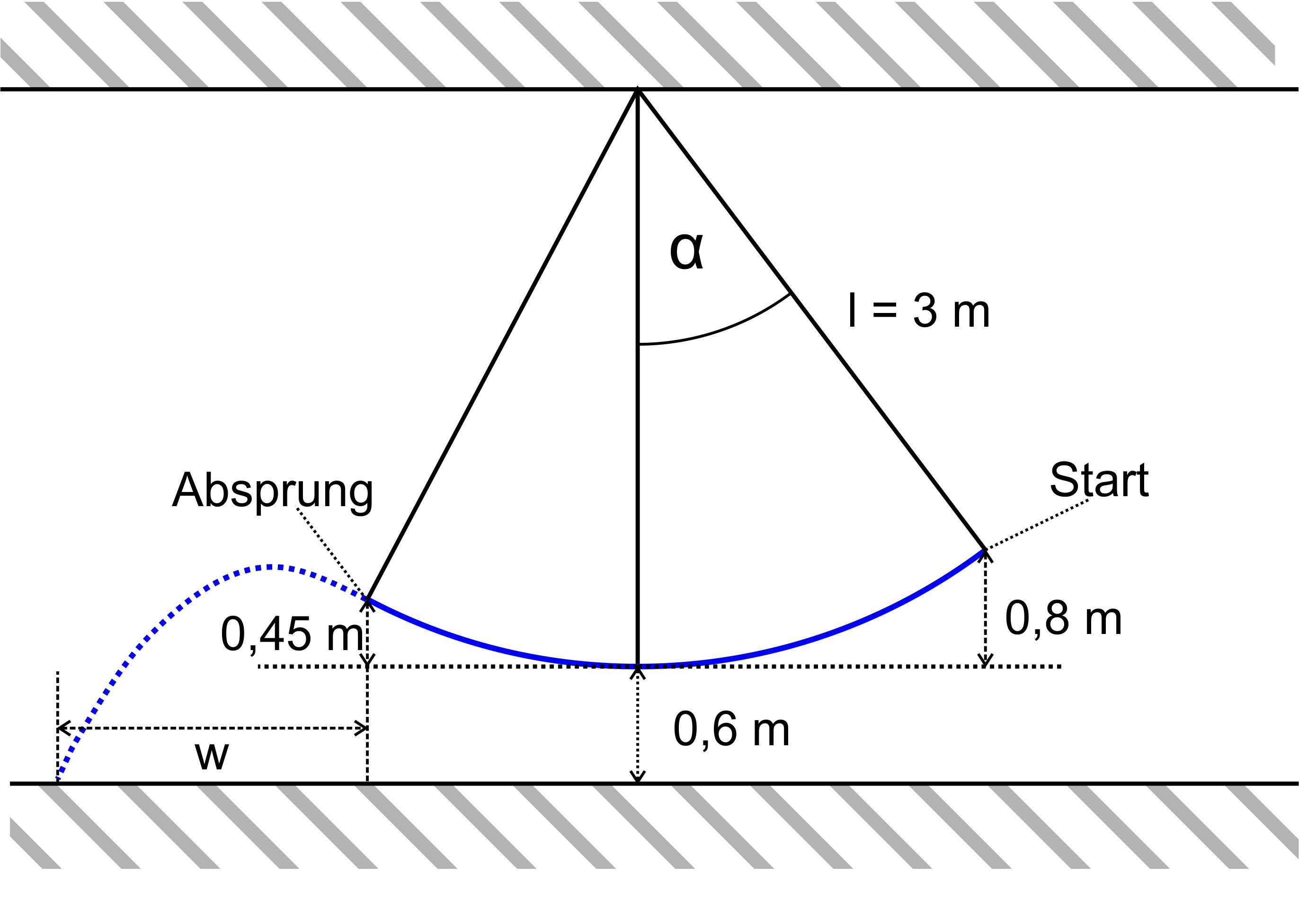
Auf einer
Schaukel der Länge l = 3 m wird ein Kind mit der Masse m = 62 kg
80 cm hochgehoben (Start) und dann losgelassen. a.) Welche
maximale Geschwindigkeit erreicht das Kind? Wie groß
ist der Startwinkel α? b.) In 45
cm Höhe springt das Kind aus der Schaukel ab und landet auf dem
Boden. Wie weit ist es gesprungen? (Beachte: Kind ist ein Massepunkt, Reibung spielt keine Rolle) Lösung: zu a.) Winkel
über Trigonometrie:
maximale Geschwindigkeit:
zu b.) komplexe Aufgabe, da man den Abwurfwinkel β
und die Abwurf- geschwindigkeit v0 benötigt
Aus dem Auslenkungswinkel beim Absprung kann man den Absprung- winkel gewinnen, wie man an folgender Abbildung (ergänzt von oben) er- kennt.
Das Kind springt in Richtung des Geschwindigkeitsvektors ab (s. Fadenpendel). Dieser zeigt senkrecht zur Aufhängung. Es gilt somit:
Jetzt kann man mit den Formeln zum schiefen Wurf weiterrechnen. Man braucht zunächst die Flugzeit, um diese dann in die Formel für die horizontale Komponente einzusetzen. Das Koordinaten- system für die Formeln zum schiefen Wurf hat seinen Ursprung im Absprungpunkt.
3.
Aufgabe: (Energieerhaltung,
Kreisbewegung, Impulserhaltung)
a.) Ein Körper der Masse m1
= 0,5 kg wird an einem Fadenpendel um eine Strecke von 30 cm gehoben.
Die Fadenlänge (bis zum Schwerpunkt) beträgt 1,5 m. Wie groß ist der Auslenkwinkel α? b.) Man lässt die Masse m1
los. Welche Geschwindigkeit hat m1 am tiefsten Punkt? Wie groß ist zu
diesem Zeitpunkt die Kraft, die am Faden zieht? (Hinweis:
vertikaler Kreis liegt vor) [Zur Kontrolle:
v1 = 2,4261 m/s] c.) Am tiefsten Punkt stößt m1
auf den ruhenden Körper m2 elastisch. Dabei verliert m1 eine
kinetische Energie von 0,8715 J. Welche Ge- schwindigkeit hat m1 nach dem Stoß? [Zur Kontrolle:
u1 = (+−) 1,5492 m/s] Mit welcher Geschwindigkeit u2
bewegt sich m2 nach dem Stoß und welche Masse hat m2? . [Zur Kontrolle: u2
= 0,8769
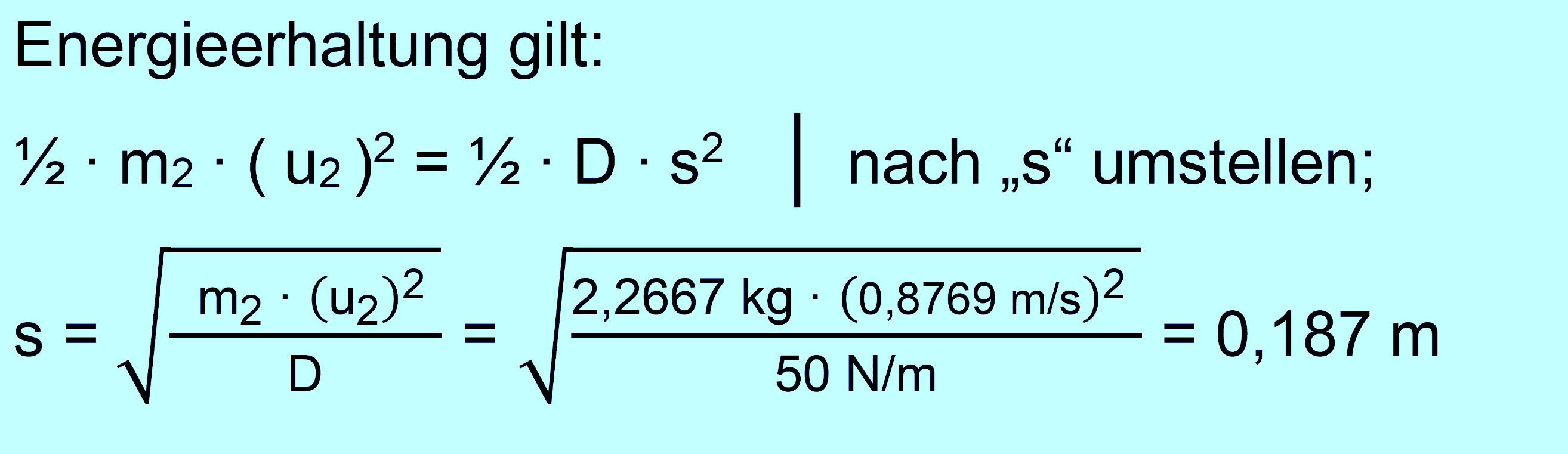
m/s ; m2 = 2,2667 kg] d.) m2 trifft nach
reibungsfreier Bewegung rechts auf eine Feder mit der Federkonstanten D = 50 N/m.
Um welche Strecke wird die Feder nach dem Auftreffen
zusammengedrückt? Lösung: zu a.) Vorgehen wie bei Aufgabe Nr.
2. a.)
zu b.) für v: Vorgehen wie bei Aufgabe Nr. 2. a.) Die Kräfte ergeben sich aus der Gewichtskraft und der Fliehkraft.
zu c.) eindeutig der schwierigste Teil der Aufgabe; für den elastischen Stoß können drei Gleichungen benutzt werden, wobei je nach Rechenweg zunächst zwei Lösungen für u1 möglich sind.
zu d.) Energieerhaltungssatz benutzen für die Spannenergie.
- zur Aufgabe Nr.1 - zur Aufgabe Nr.2 - zur
Aufgabe Nr.3 |