Übungsaufgaben

1. Aufgabe ( Energieerhaltung, schiefer Wurf, Trigonometrie)

Bei einer Kinderschaukel liegt man im tiefsten Punkt (Tiefpunkt)

eine Geschwindigkeit von 3,5 m/s vor.

(Bei den Berechnungen davon ausgehen, dass sich die Masse in einem Punkt auf der Schaukel befindet)

a.) Berechnen Sie die größte Höhe (gemessen vom Tiefpunkt aus), die man bei

der Schaukel erreichen kann.

b.) Wenn man am tiefsten Punkt aus der Schaukel springt, hat man

beim Auftreffen auf dem Erdboden eine Geschwindigkeit von 5,1 m/s.

In welcher Höhe über dem Erdboden ( h_T) befindet sich der tiefste

Punkt der Schaukel?[Zur Kontrolle: h_T = 0,70 m ).

c.) Man springt in einer Höhe von 30 cm über dem Tiefpunkt aus der

Schaukel. Berechnen Sie die Absprunggeschwindigkeit v₀. 1,12 m ist

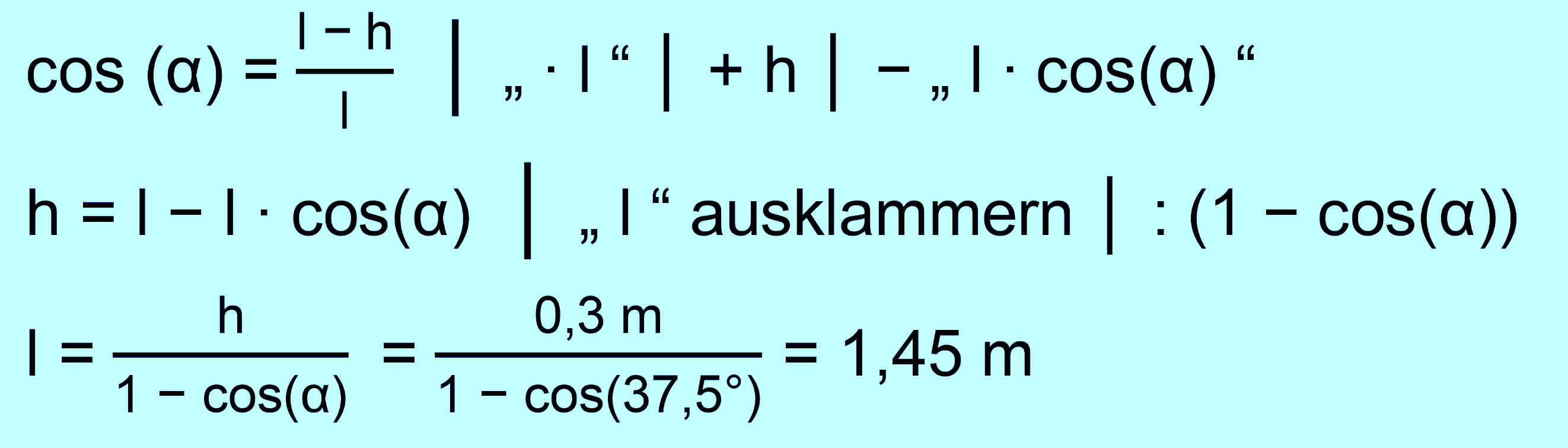
die größte Höhe, die man dabei über dem Erdboden erreicht. Berechnen Sie den Absprungwinkel α. [Zur Kontrolle: v₀ = 2,52 m/s, α = 37,5°]

d.) Berechnen Sie am Schluss noch die Seillänge der Schaukel.

Lösung:

zu a.)

zu b.)

zu c.)

zu d.)

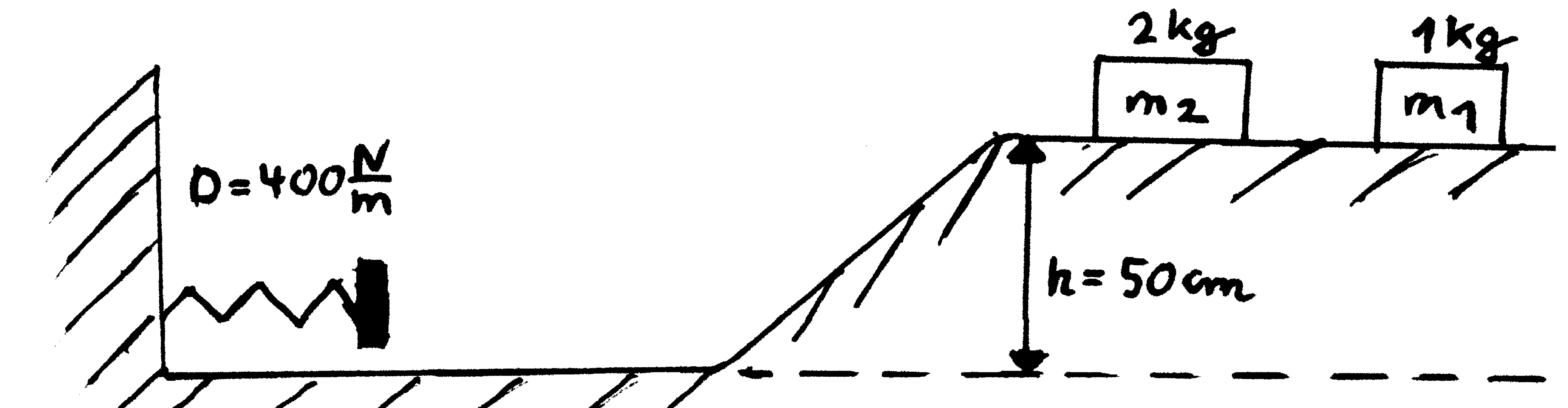
2. Aufgabe ( Impulsformel, Energieerhaltungssatz)

Die Masse m₁= 1 kg stößt mit der Geschwindigkeit v₁= 3 m/s voll-

kommen elastisch auf die ruhende Masse m₂= 2 kg. Danach ge-

langt m₂ über die schiefe Ebene zur linken Feder (D = 400 N/m). [Zur Kontrolle: v₂(unten) = 3,716 m/s]

Bestimmen Sie die Strecke, um die die Feder nach dem Auftreffen zusammengedrückt wird? Hinweis: es liegt keine Reibung vor.

Lösung:

- zurück zu den Komplexaufgaben