Trägheitskräfte-Zentrifugalkraft-Fliehkraft

Im vorherigen Kapitel haben wir uns mit der Radialkraft oder Zentripetal-

kraft beschäftigt. Diese Kraft ist notwendig, da sich ein Körper aufgrund

seiner Trägheit immer geradlinig gleichförmig bewegen will. Von außen

betrachtet muss es diese Kraft geben, da sich der Körper sonst wegen

des Trägheitssatzes nicht auf einer Kreisbahn bewegen würde. Bei einer

gleichförmigen Kreisbewegung zeigt die Radialkraft senkrecht zur Bewe-

gungsrichtung, also senkrecht zur Geschwindigkeitsrichtung, somit

immer radial zum Mittelpunkt des Kreises.

Diese Kraft wird bei vielen Kirmesfahrgeschäften durch die Seitenwände

(Round up, Rotor usw.) oder durch eine Kette (Kettenkarussell), Stange

bzw. Faden aufgebracht.

Befindet man sich selber im Fahrgeschäft, also im rotierenden System,

hat man häufig einen ganz anderen Eindruck. Man hat das Gefühl nach

außen gedrückt zu werden. Diese „Kraft“ wird Fliehkraft oder Zentri-

fugalkraft genannt.

Im System scheinen eher folgende Verhältnisse vorzuliegen:

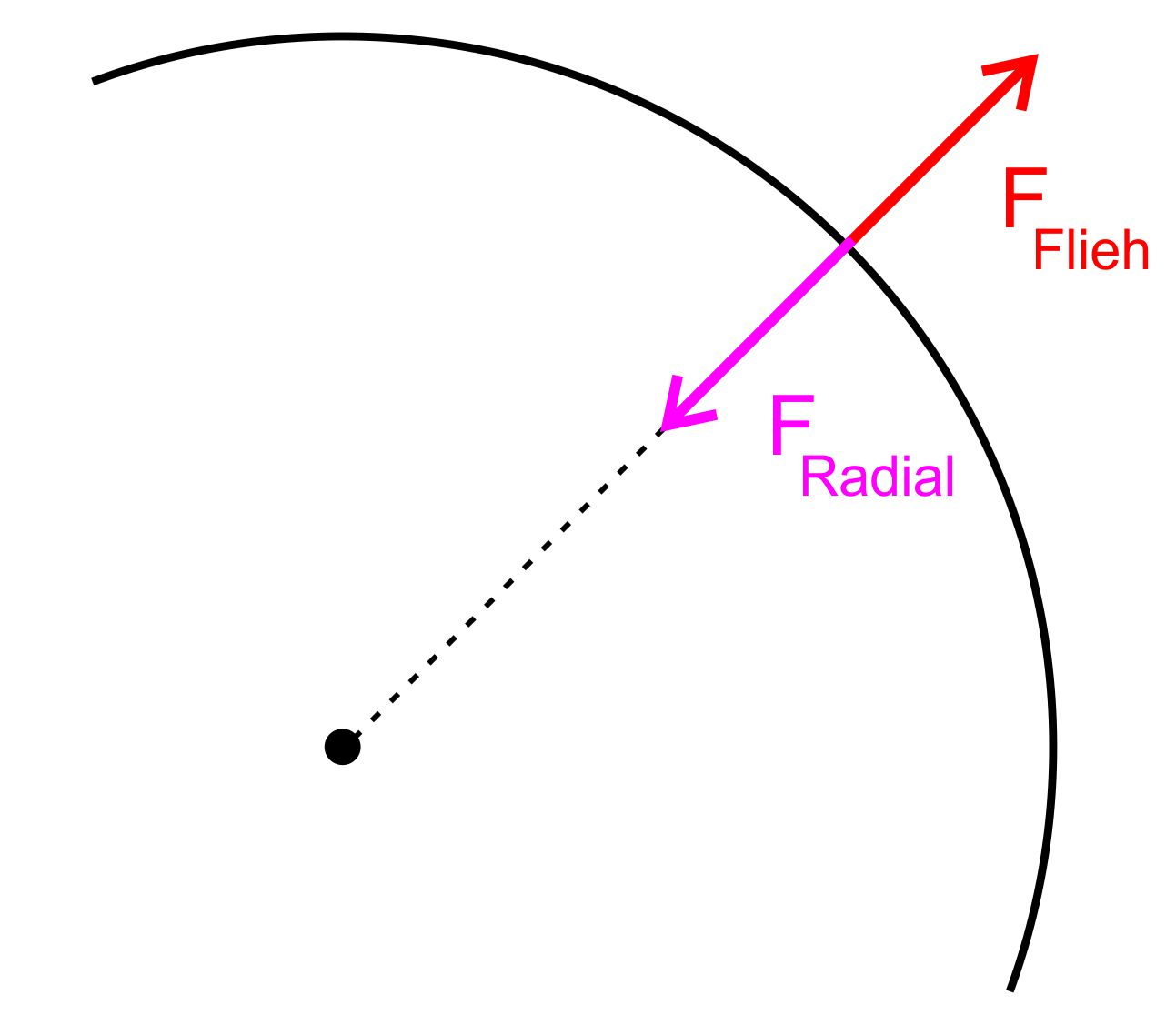
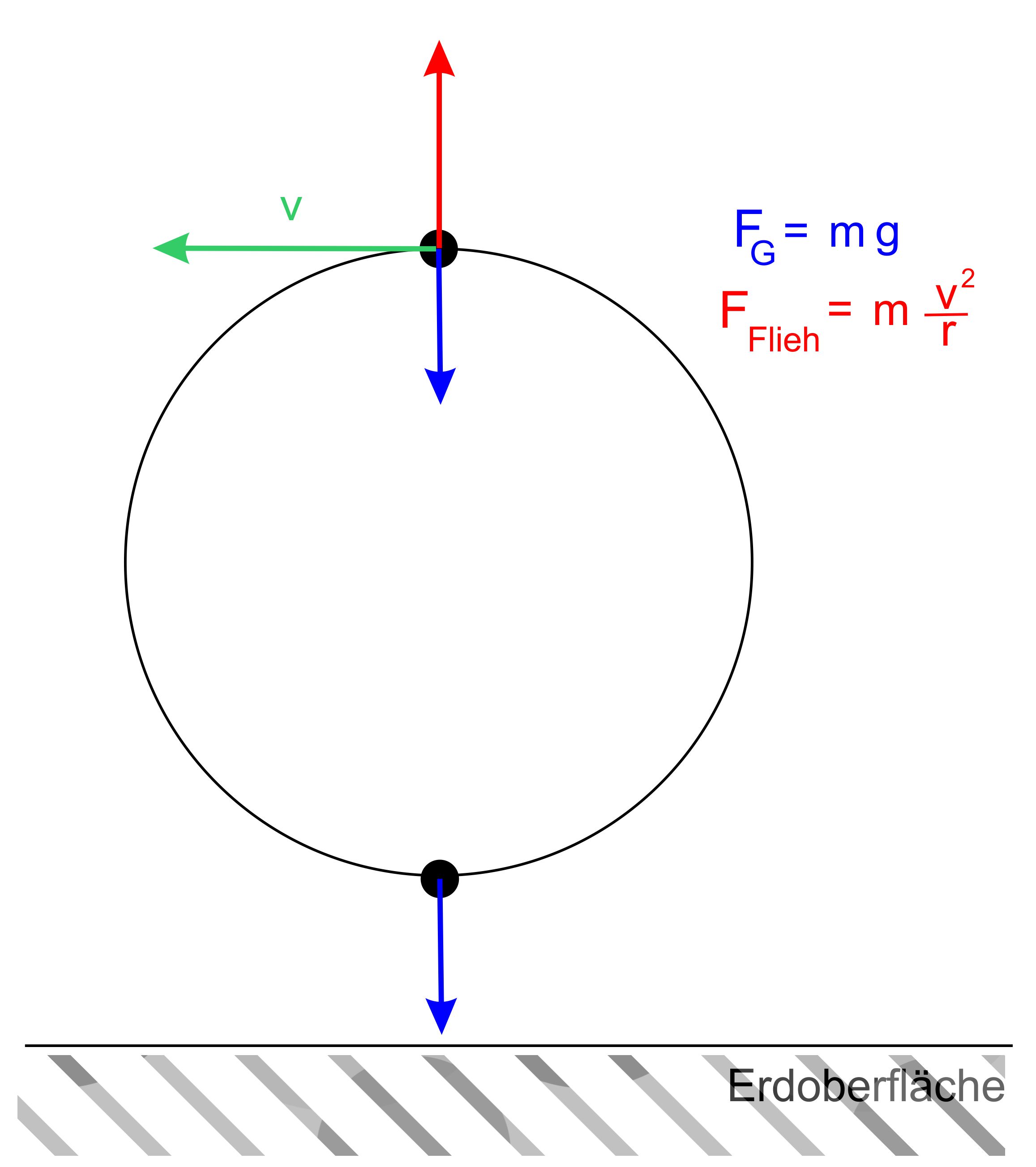
Es gibt zunächst am Anfang der Rotation eine radial nach außen ge-

richtete Fliehkraft. Von dieser Kraft wird man gegen die Außenwände

gepresst, so dass diese Wände dann die Radialkraft aufbringen. Es

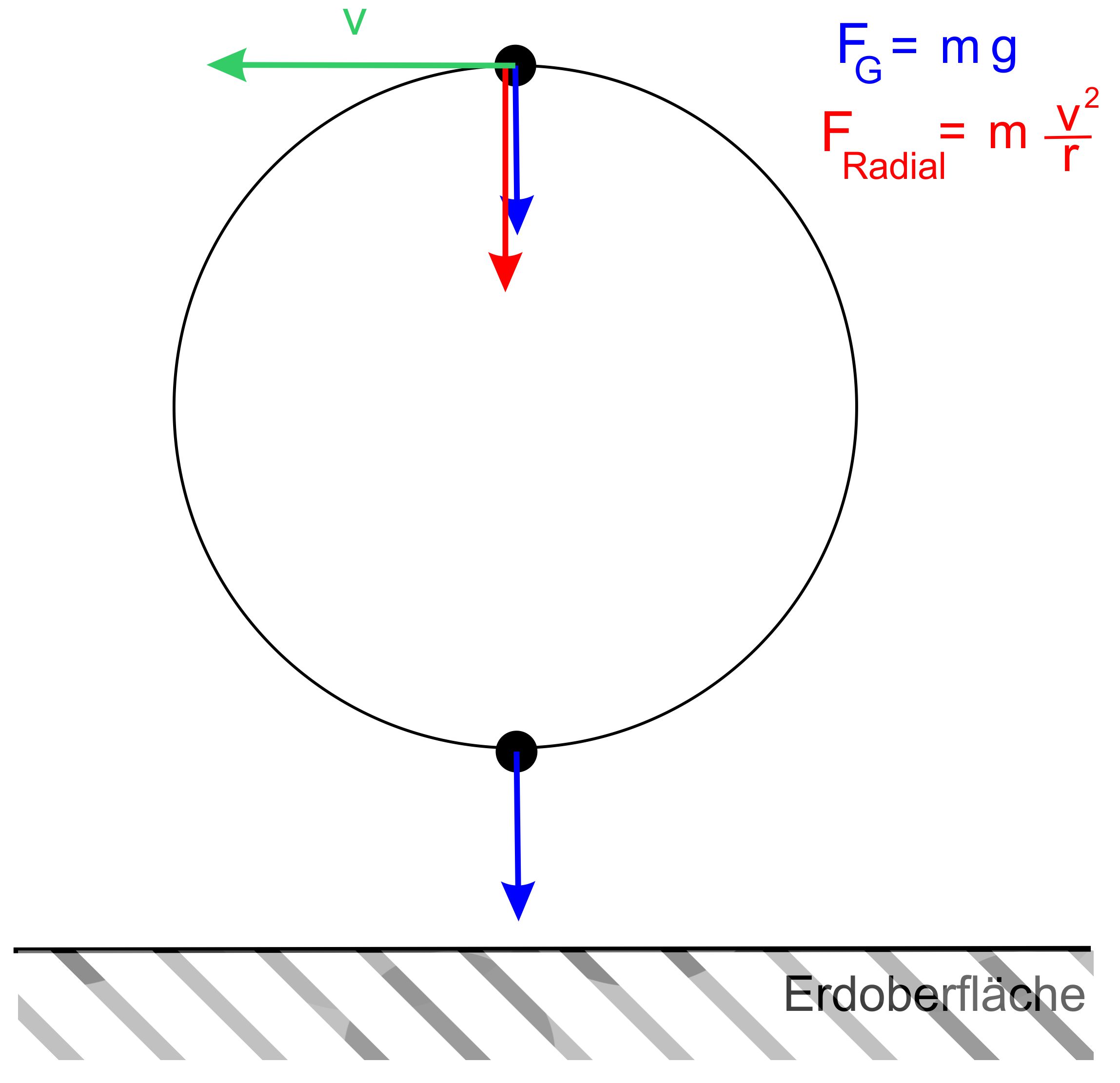
herrscht ein Kräftegleichgewicht zwischen Fliehkraft und Radialkraft.

Die Abbildung zeigt die Verhältnisse noch einmal.

Wenn „echte Kräfte“ vorliegen, müssen allerdings die Newtonschen

Axiome zutreffen, insbesondere das 3. Newtonsche Axiom ( actio =

reactio ). Dies bedeutet, wenn eine Kraft von einem Körper A auf einen

Körper B ausübt wird, gibt es auch eine gleich große Kraft von B auf A.

Schauen wir uns hierzu noch einmal die beiden Kräfte an.

Zunächst zur Radialkraft:

Vom Mittelpunkt M aus wird (z.B. über einen Faden) eine Kraft F_A auf die

Masse m ausgeübt. Dann muss jetzt auch m eine Kraft F_B auf den Mittel-

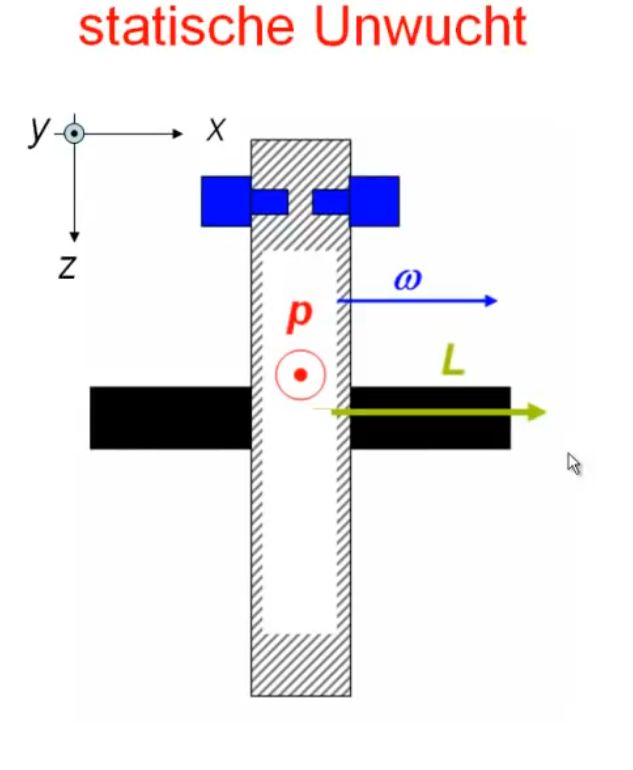
punkt M ausüben. Diese Kraft gibt es tatsächlich. Sie zieht nämlich immer

am Drehlager. Man spricht von der „Unwucht“. Diese Unwucht kann auf

Dauer zu Schäden am Lager führen.

Hierzu noch ein einfaches Beispiel aus dem Alltag:

Man bewegt mit der Hand ein Massestück an einem Faden auf einer

horizontalen Kreisbahn über dem Kopf. Die Hand übt über den Faden

eine Radialkraft auf die Masse aus. Gleichzeitig bemerkt man, dass die

Hand immer in Richtung der Masse gezogen wird. Man kann die Hand

nicht ruhig halten. Dies ist die „Unwucht“, die für keine ruhige Rotation

sorgt.

Hinweis: Wer noch mehr über „Unwuchten“ erfahren will, kann sich dieses Video ansehen.

Quelle: https://www.youtube.com/watch?v=LdexQo-xmOg

Hinweis: sehr wissenschaftliches Video,

die Abbildungen zeigen schön die

fehlende Symmetrie

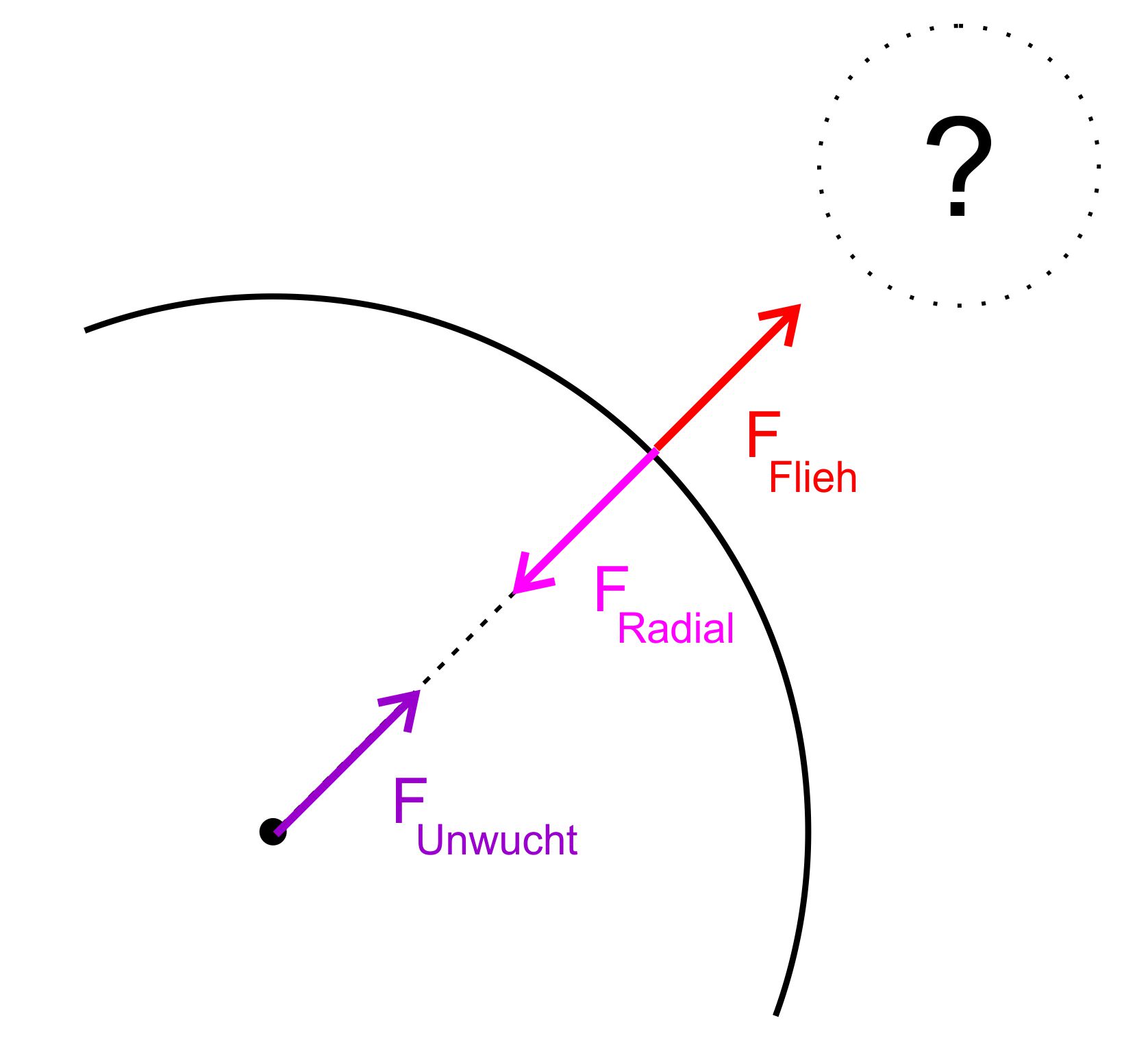
Jetzt zur Fliehkraft:

Falls es sich um eine „echte“ Kraft handelt, müsste hier auch das 3.New-

tonsche Axiom gelten. Dies passt aber offensichtlich nicht, denn man

müsste außerhalb des Kreises einen Körper geben, der diese Kraft aus-

übt. Diesen Körper gibt es aber nicht! Man findet somit auch keine korres-

pondierende Kraft (reactio) zur Fliehkraft. Das 3.Newtonsche Axiom ist

verletzt.

Wenn also Fliehkräfte keine „echten“ Kräfte sind, warum haben wir dann

„das Gefühl“, das diese Kraft existiert, wenn wir uns im rotierenden Sys-

tem befinden. Ein Betrachter von außen kann die Frage sofort beant-

worten: „Diese Kraft ist allein auf die Trägheit zurückzuführen“.

Deshalb spricht man auch von Trägheitskräften oder Scheinkräften.

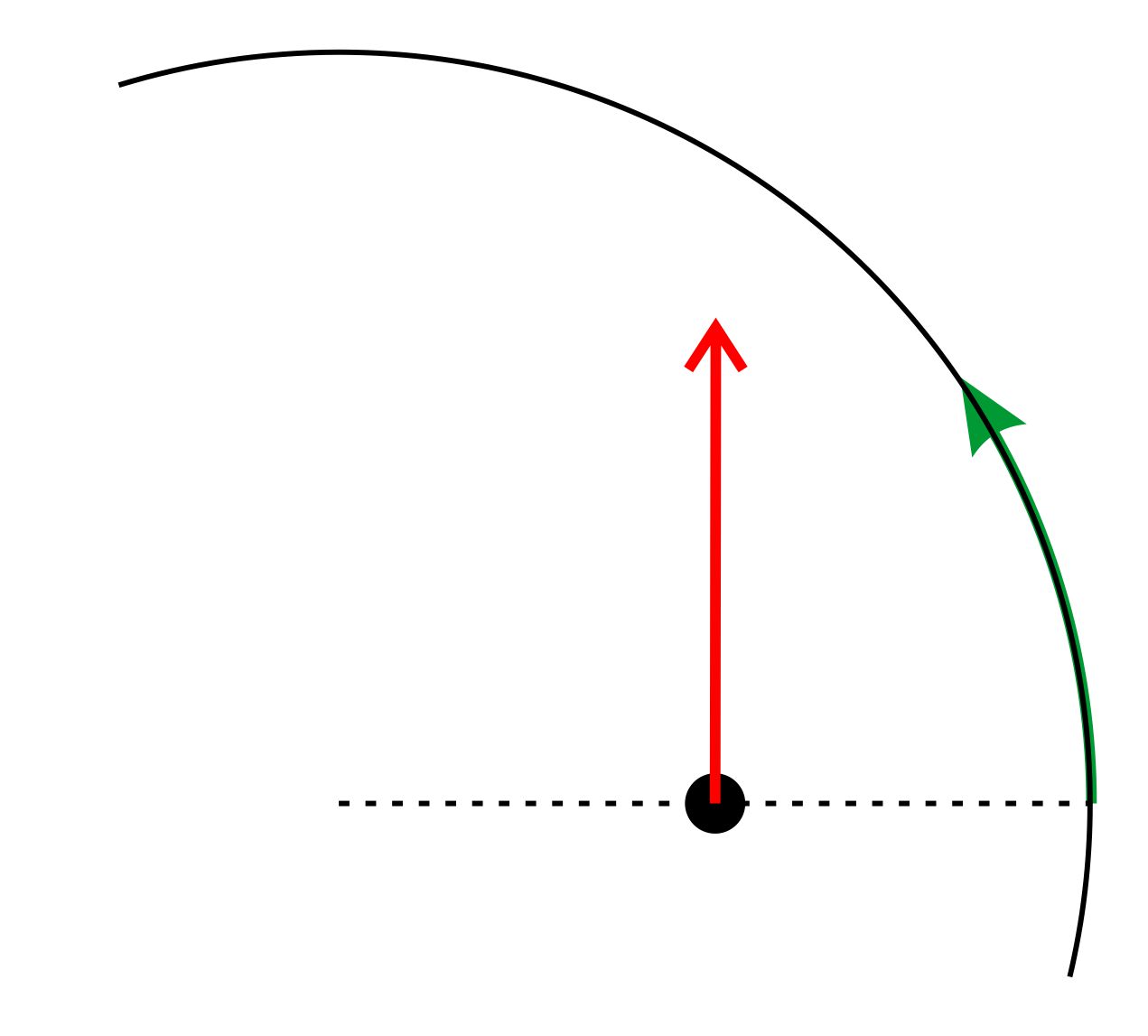
Wir betrachte das Ganze mal am Beispiel des Fahrgeschäftes „Musikexpress“:

Man setzt sich in das Fahrgeschäft hinein. Der Musikexpress startet. Wir

wollen uns nach Trägheitssatz geradlinig weiterbewegen. Die Wände

bewegen sich aber auf einer Kreisbahn. Also bewegen wir uns auf die

Wände zu. Wir haben das „Gefühl“ uns auf die Wände zuzubewegen.

Eine „Kraft“ scheint uns zur Wand zu „drücken“. Diese Kraft ist aber letzt-

endlich nur auf unsere Trägheit zurückzuführen.

Die Verhältnisse noch einmal in einer Abbildung:

Da die Fliehkraft aus physikalischer Sicht „verzichtbar“ ist, um die Kreis-

bewegung zu erklären, könnte man sie auch gar nicht erwähnen. Es gibt

z.B. einige Physikbücher, die so vorgehen.

Da wir aber ein „Gespür“ für diese „Kraft“ haben, lassen sich viele Übungs-

aufgaben häufig einfacher berechnen, wenn man diese „Kraft“ zulässt.

Rotierender Wassereimer

Ein mit Wasser gefüllter Eimer soll auf einem vertikalen Kreis

(s. dort) bewegt werden. Wie groß muss die Geschwindigkeit mindestens sein, damit man nicht nass wird?

Folgendes Video verdeutlicht den Versuch:

Quelle: Ausschnitt aus dem Video:

https://www.youtube.com/watch?v=AUG_wKS75qw

1. Betrachtung mit Radialkraft:

Auf den Eimer und somit auch das Wasser wirkt in jedem

Punkt die Gewichtskraft, die die Masse (das Wasser) zum

Erdmittelpunkt zieht.

Würden wir den Eimer einfach ohne Kreisbewegung über

den Kopf halten, würde das Wasser ausfließen und wir eine

Dusche erhalten.

Mit der Kreisbewegung tritt eine Radialkraft auf, die bei ge-

nügend großer Geschwindigkeit v zu einer Kreisbahn führt,

also auch das Wasser auf die Kreisbahn zwingt. Ist v zu

klein, kommt es zu keiner Kreisbahn, sondern die Bahn wird

abgebrochen bzw. ein Faden würde zusammenklappen und

nicht gespannt bleiben. Hierzu ist zu beachten (s. vertikaler

Kreis), dass die Geschwindigkeit mit der Höhe über dem

Erdboden abnimmt.

Das Problem beim vertikalen Kreis ist, dass in jedem Punkt

der Kreisbahn zwei Kräfte wirken, einmal die Normalkraft des

Eimerbodens, die immer zum Mittelpunkt zeigt, und die

Gewichtskraft. Komponenten der Gewichtskraft können da-

bei die Normalkraft unterstützen oder mindern, je nachdem

in welchem Punkt der Kreisbahn man sich befindet. Die ge-

naue Formel für die zum Mittelpunkt zeigende Radialkraft F_R

lautet:

Diese Formel wird am Beispiel „Looping“ in folgendem Video

hergeleitet:

Quelle: https://www.youtube.com/watch?v=egOeIZjiFEA

Im obersten Punkt gilt α = 180°, somit cos(180°) = − 1. Die

Gewichtskraft „unterstützt“ also die Muskelkraft, um die

Radialkraft aufzubringen. Im Idealfall wird die Radialkraft nur

durch die Gewichtskraft geleistet, es braucht dann keine

Muskelkraft aufgewandt werden. In diesem Fall gilt also:

2. Betrachtung mit Fliehkraft

Die Betrachtung mit der Fliehkraft ist deutlich einfacher. Die Fliehkraft zeigt immer radial nach außen. Die Gewichtskraft

weist immer zum Erdmittelpunkt.

Wenn die Fliehkraft am obersten Punkt kleiner ist als die Ge-

wichtskraft fließt das Wasser aus. Mit zunehmender Geschwin-

digkeit wird die Fliehkraft immer größer bis sie der Gewichtskraft

die Waage hält. Dies ist dann die minimalste Geschwindigkeit,

die man erreichen muss, damit man nicht nass wird. (Rechnung

wie oben)

Liste von Links: noch keine z.Z.

Übungsaufgaben (in Arbeit)

Nächstes Kapitel: Besondere Kreisbewegung