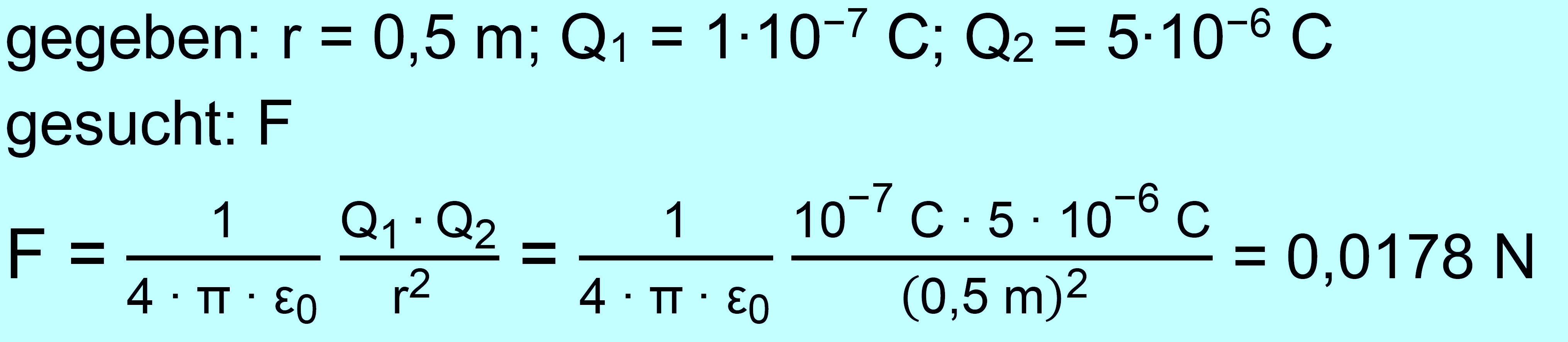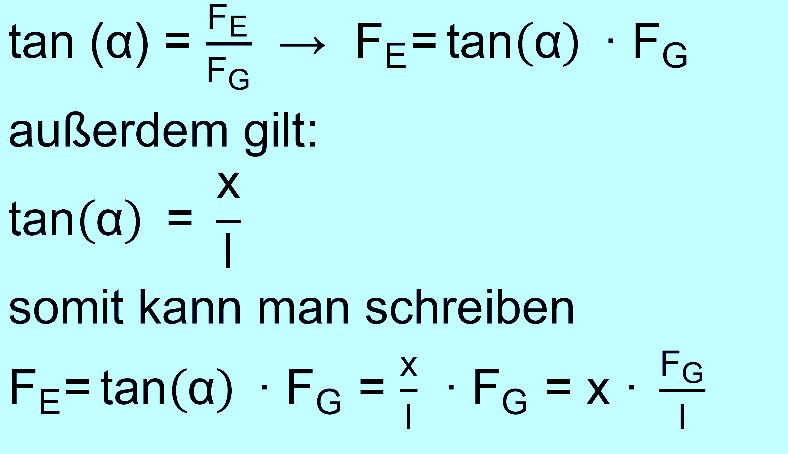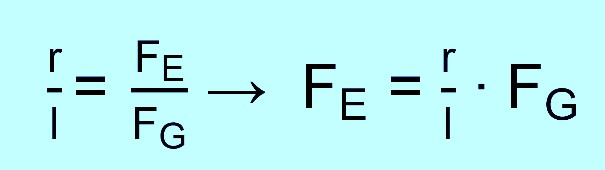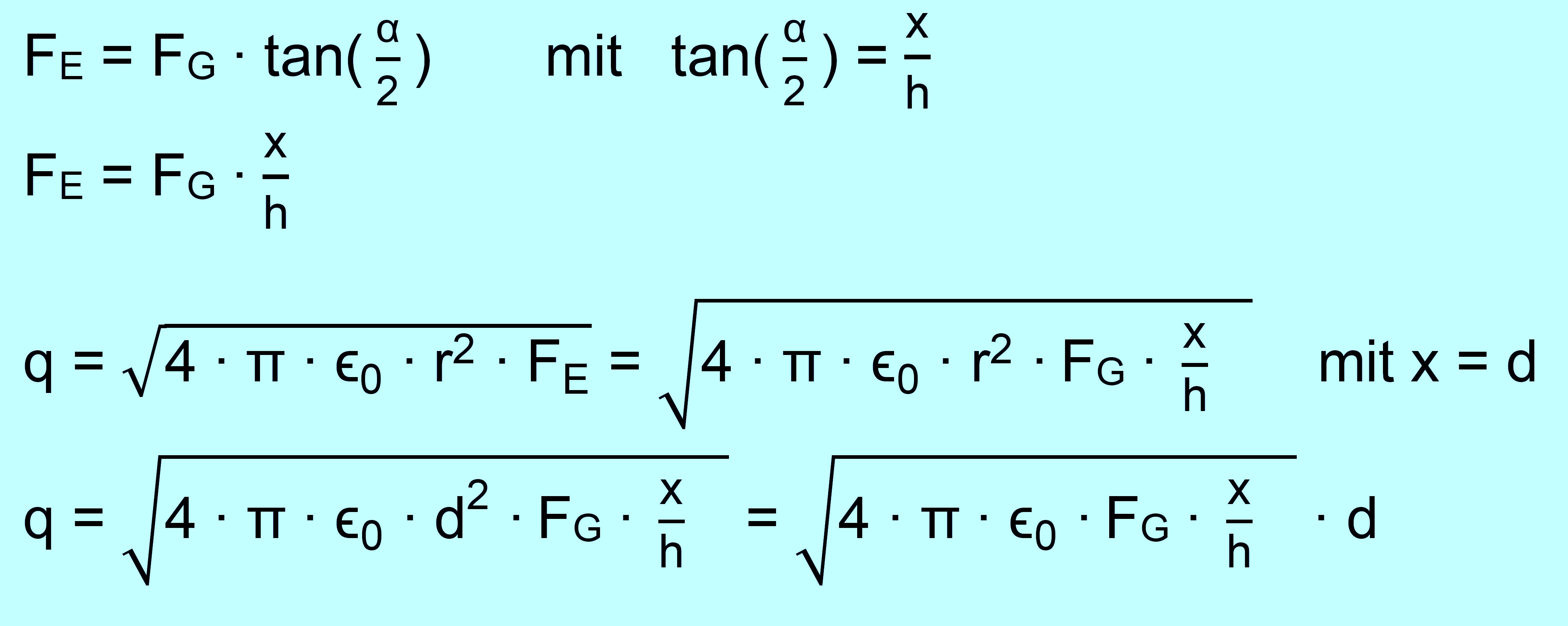|
Übungsaufgaben-Coulomb Aufgabe Nr.1 (leicht, mittel, leicht) a.) Zwei Kugeln sind 50 cm voneinander entfernt. Die eine Kugel trägt
die Ladung Q1 = 10−7
C, die andere die Ladung Q2 = 5 ∙10−6
C. Wie groß ist die Kraft F, welche die
Kugeln aufeinander ausüben? b.) Zwei Kugeln, deren Mittelpunkte 10 cm entfernt voneinander
liegen, üben eine Kraft von 300 N
aufeinander aus. Wie groß sind die Kräfte, wenn die Kugelmittelpunkte einen
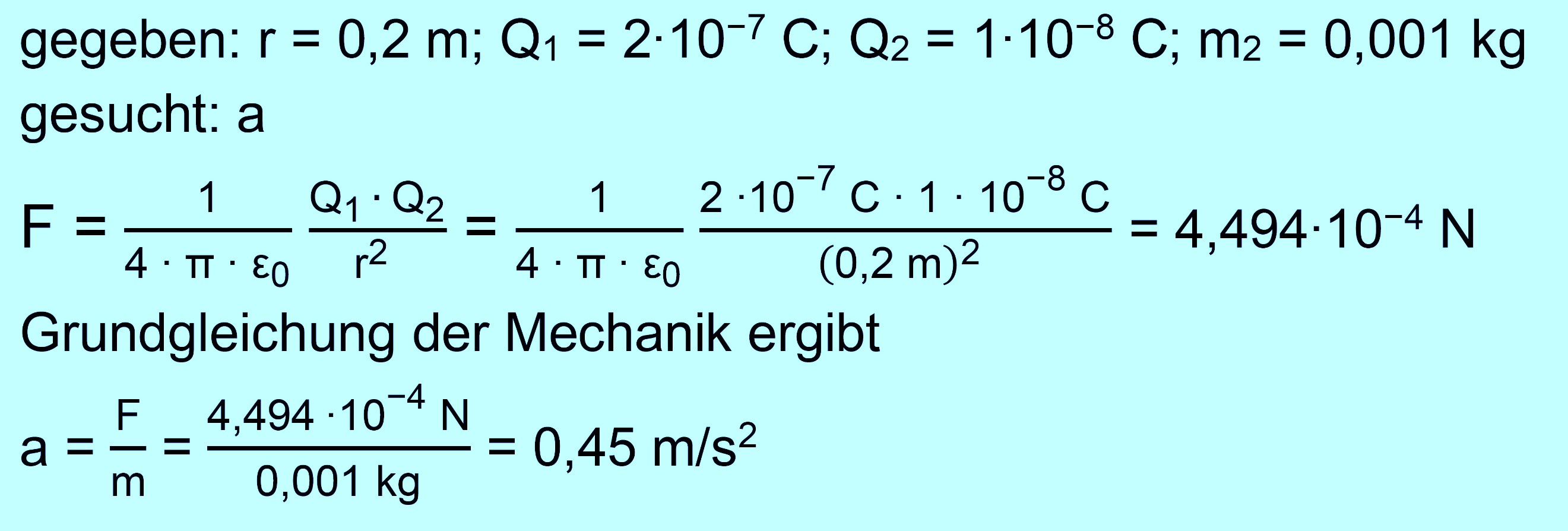
Abstand von 50 cm aufweisen? c.) Eine Konduktorkugel trägt die Ladung Q
= 2 ∙ 10−7 C. In ihrer
Nähe hängt (Abstand 20 cm) isoliert
eine kleine Alukugel, auf die eine Ladung q = 10−8 C
aufgebracht wird. Mit welcher Anfangsbeschleunigung ver- lässt die Alukugel
ihre Ruhelage? Die Kugelmittelpunkte liegen in einer horizontalen Ebene. Die Masse der
Alukugel beträgt 1 g. Lösungen: zu a.) einfach die Formel zum
Coulomb-Gesetz benutzen
zu b.) erst umstellen, da die
Ladungen fehlen
zu c.) neben dem Gesetz von
Coulomb muss die
Grundgleichung der Mechanik benutzt werden.
Aufgabe
Nr.2 (sehr
schwer) An einem langen isolierenden
Faden ( l = 4 m ) hängt ein Probekörper ( m = 0,5 g ; q = 6,4 ∙ 10−8
C ). Schiebt man eine gleichnamige geladene Kugel ( R
= 2 cm ) an ihn heran, bis diese sich an dem ursprünglichen Ort des Probekörpers befindet,
wird der Probekörper um die Strecke 12 cm ausgelenkt. Wie groß ist die Ladung der
Kugel? Wie groß ist ihre Flächenladungs- dichte? Wie groß ist die
Feldstärke an ihrer Oberfläche, wie groß am Ort des Probekörpers? Man halbiert nun die Ladung des
Probekörpers, indem man ihn mit einem ungeladenen, gleichen
Kügelchen berührt. Welche Auslenkung liegt jetzt vor? Lösung: Man muss zunächst die Kraft
auf den Probekörper bestimmen. Es gibt hierzu zwei
Möglichkeiten: 1. Fall: Es wird eine Näherung vorgenommen, da die Fadenlänge sehr groß gegenüber der Auslenkung ist→ der
Probekörper bewegt sich praktisch auf einer horizontalen Linie; es liegen
die Verhältnisse wie im 2.Experiment
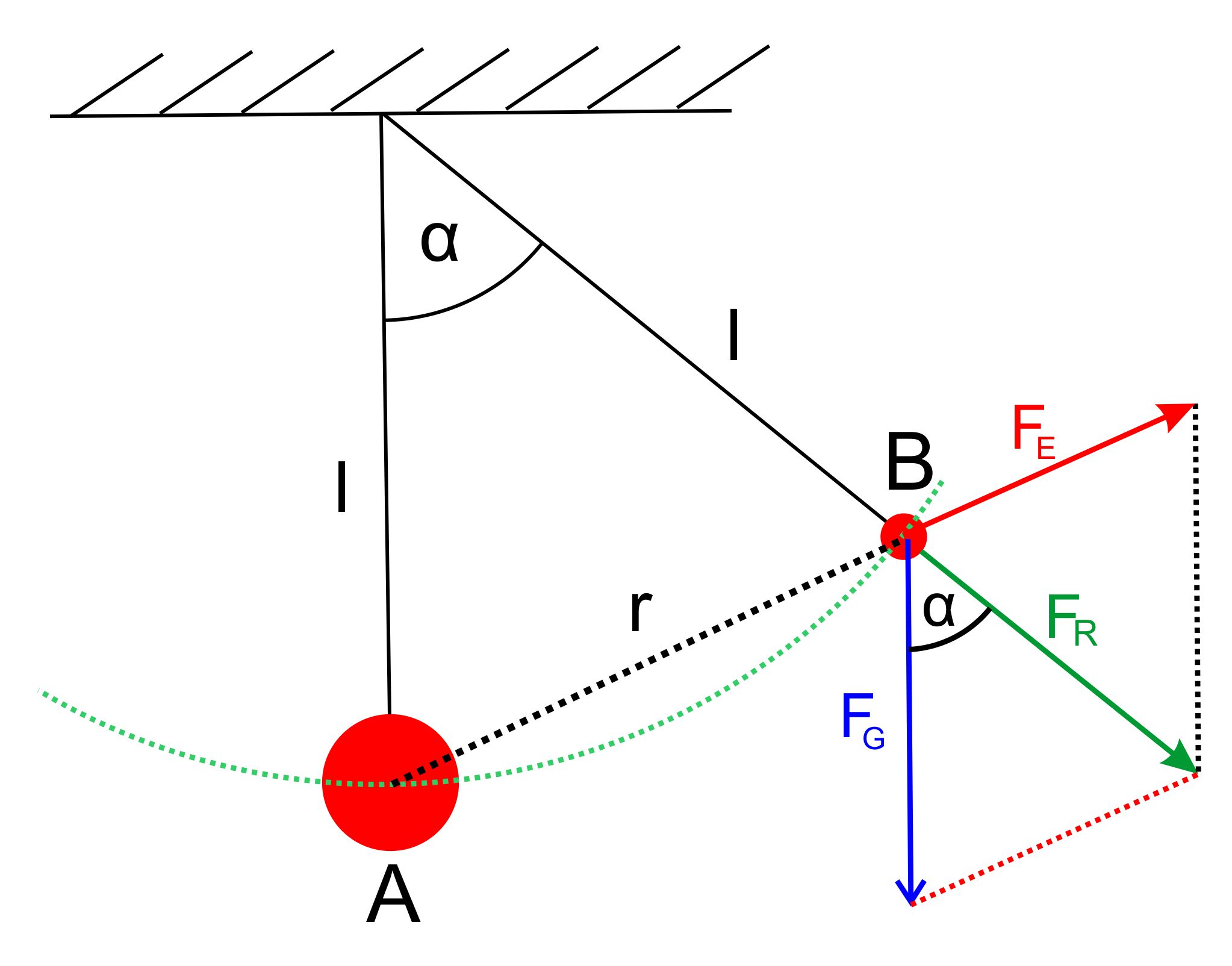
zum Coulombschen Gesetz vor. Ich übernehme die Darstellung von dort. Für die
Kräfte gilt dann folgendes Kräfteparallelogramm:
Aus der Kraft ergibt sich
durch Umstellen des Coulombschen Gesetzes die Ladung der Kugel. Einsetzen
in die Formeln für die Flächenladungs- dichte und Feldstärke ergibt
dann die gesuchten Werte.
2. Fall: Es wird keine
Näherung vorgenommen. Der zweite Fall trifft dann auch für kurze
Fadenlängen zu. Annahme: Der Probekörper
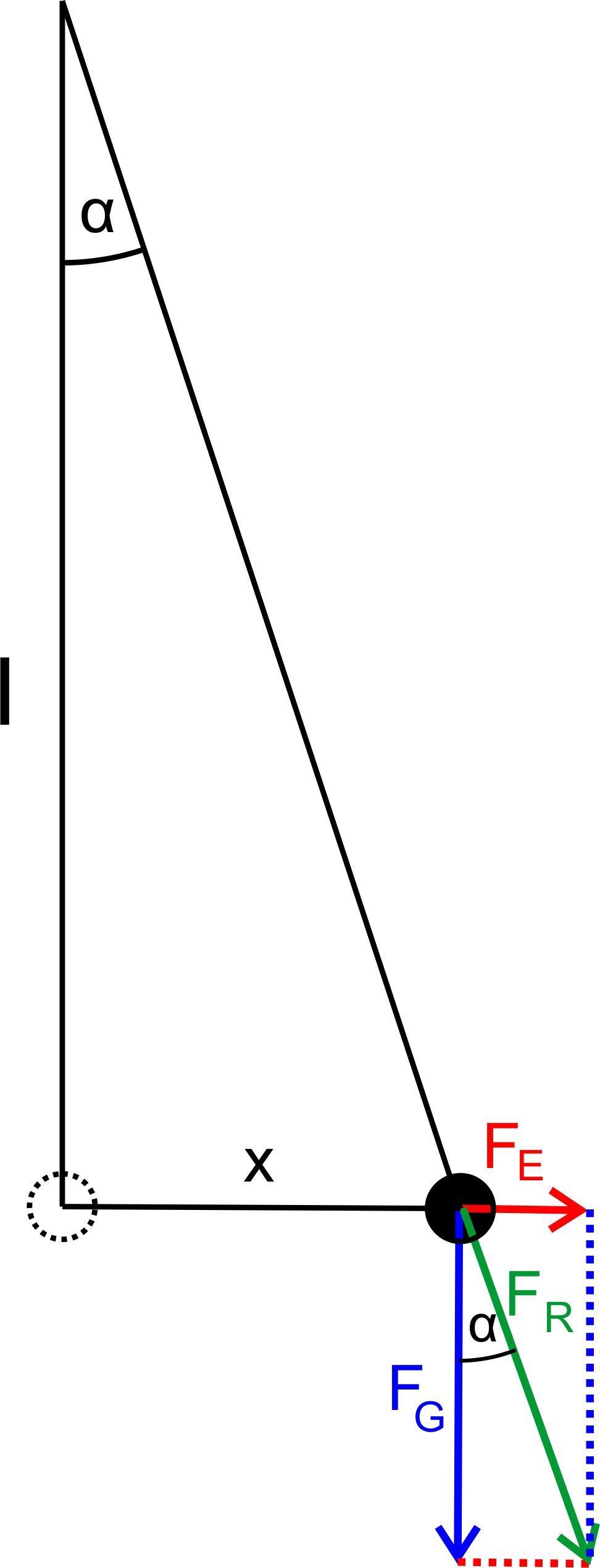
verschiebt sich auf einem Kreisbogen und wird merklich angehoben. Es gilt weiterhin: Der
Faden stellt sich so ein, dass die resultierende Kraft FR
aus elektrischer Feldkraft FE und Gewichtskraft FG
entlang des
Fadens zieht. Wir haben die gleichen
Verhältnisse wie in der Klausuraufgabe
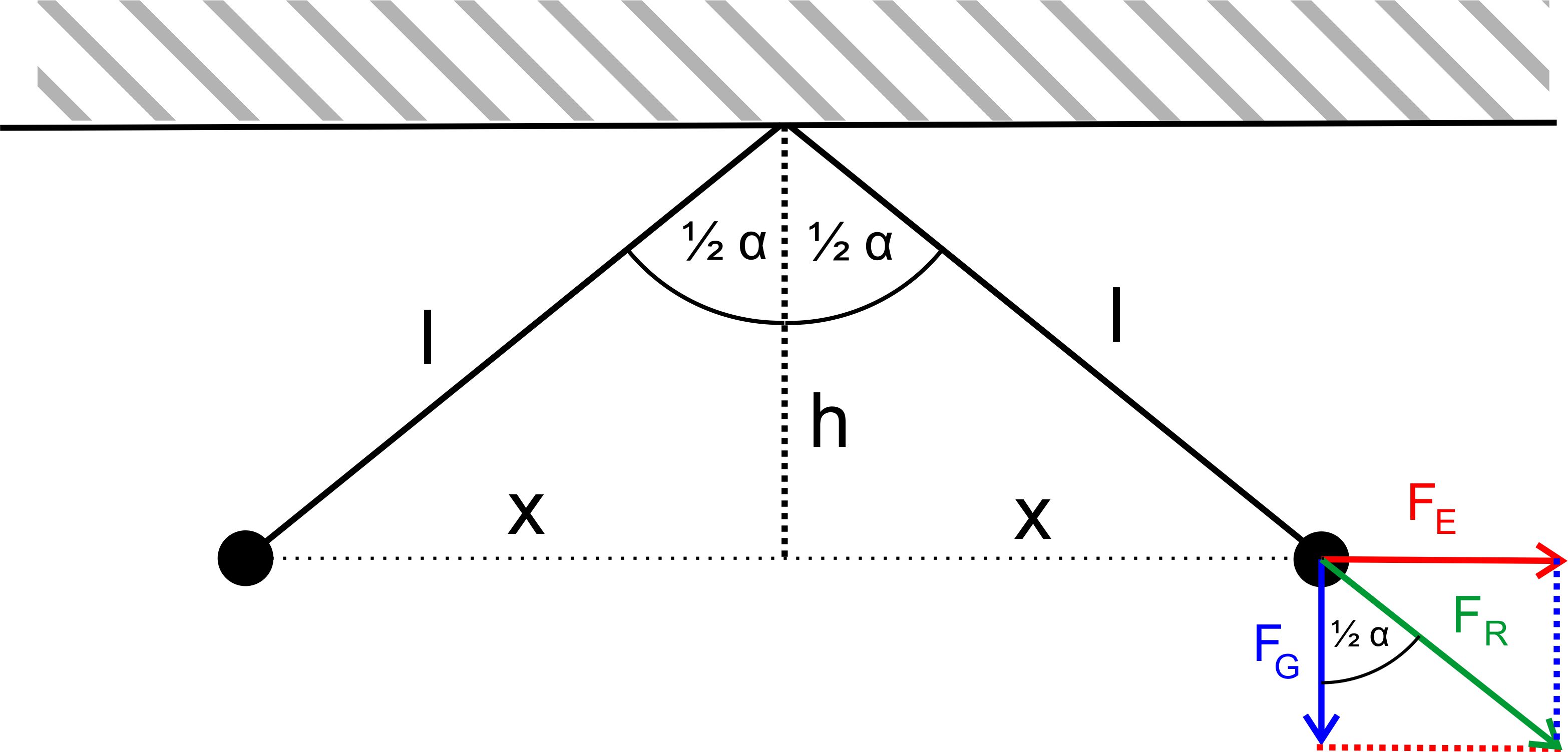
zu den Kräften im E-Feld Teil 2. Wir übernehmen die entsprechenden Überlegungen. hier
zunächst die Skizze der Kräfte
Da die
Fadenlänge l bleibt, liegt ein
gleichschenkliges Dreieck vor. Mit dem Strahlensatz
ergibt sich dann sofort:
Wir müssen also genauso
rechnen wie im 1.Fall. Nur das wir jetzt eine ganz allgemeine Formel
gefunden haben, die für jede Fadenlänge gilt. 2.Teil „Halbierung der Ladung“
Aufgabe
Nr.3
(schwer) Zwei Alukugeln mit gleichem Radius
und gleicher Masse m sind so an gleich langen Isolierfäden mit
gleichem Aufhängepunkt aufgehängt, dass sie einander berühren. Auf jede Alukugel
wird die Ladung q über- tragen. Die Kugeln stoßen sich ab
und kommen in einer Entfernung d = 2 x zur Ruhe. Wie lässt sich
die Ladung q aus den messbaren Größen l, m, x und d bestimmen? Welche Ladung hat jede Kugel,
wenn d = 10 cm, l = 2 m und m = 2 g ist? Lösung: Wir
haben die gleichen Verhältnisse
wie in der Klausuraufgabe zu den Kräften
im E-Feld Teil 3. Wir
übernehmen die entsprechenden Über- legungen.
aus der Aufgabe Nr. 2 (1. Fall) und dem Gesetz von Coulomb
ergibt sich der Lösungsweg
Alternative: Man kann sich auch direkt
an der Klausuraufgabe Teil 3 Lösung orientieren und kommt dann
auch über α zur Lösung, nämlich
- zu Aufgabe Nr.1 - zu Aufgabe Nr.2 -
zu Aufgabe Nr.3 |