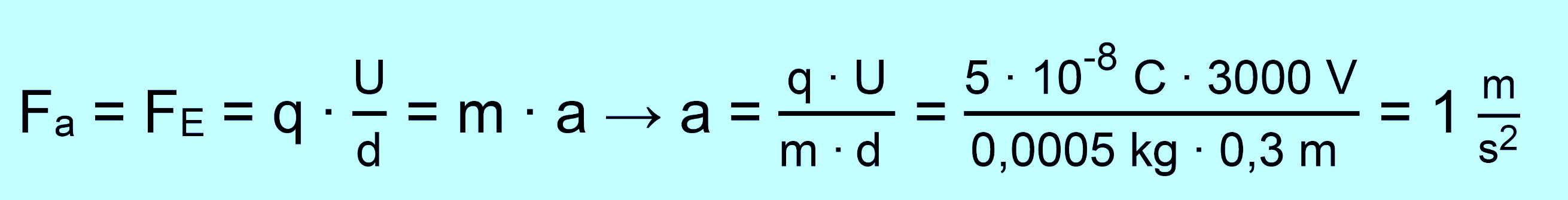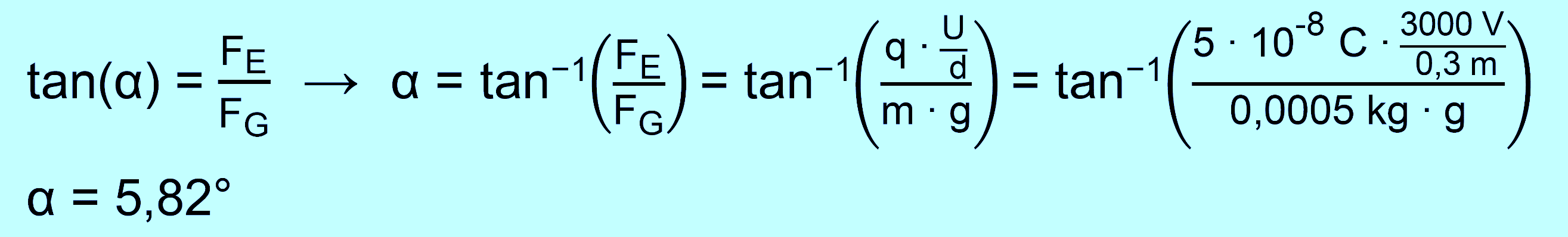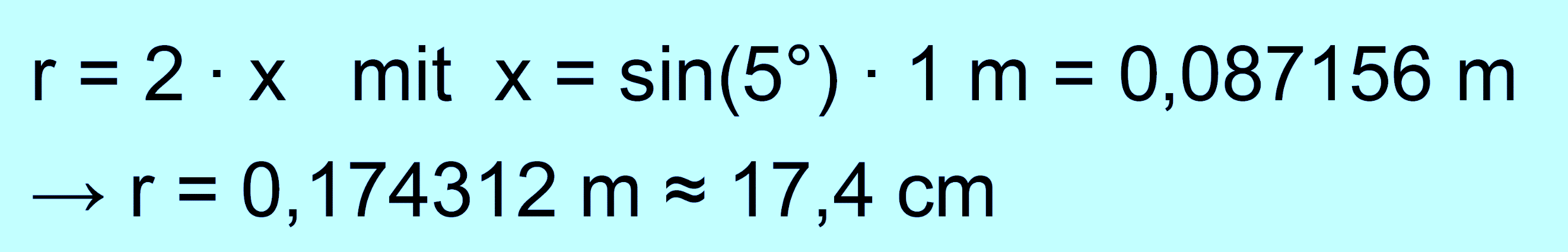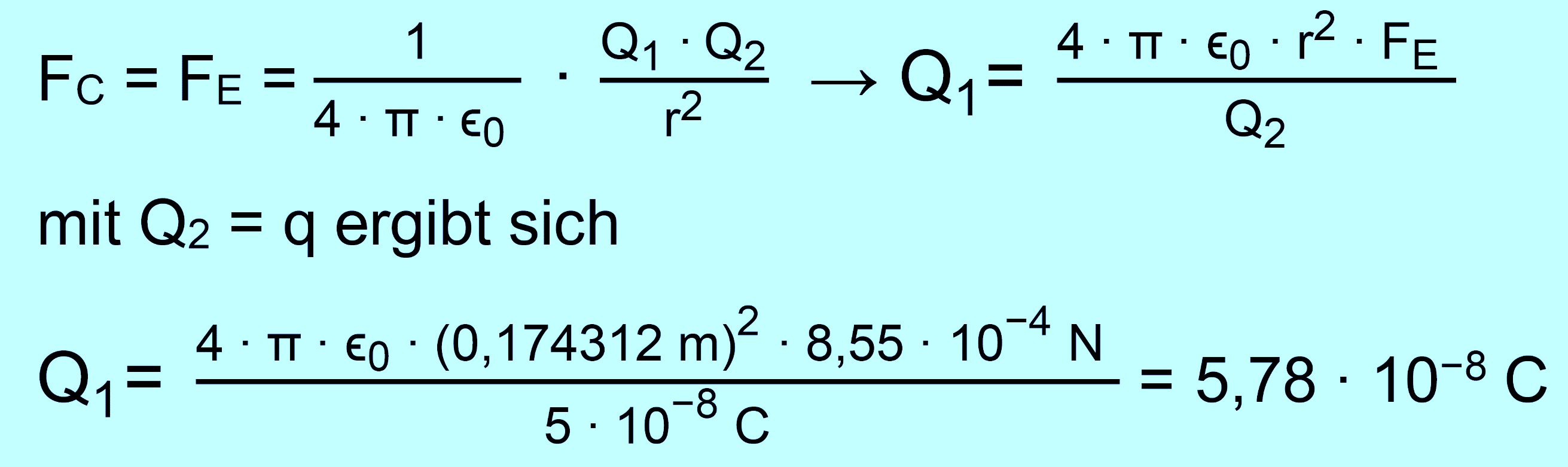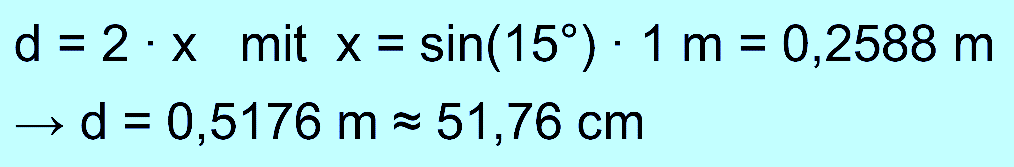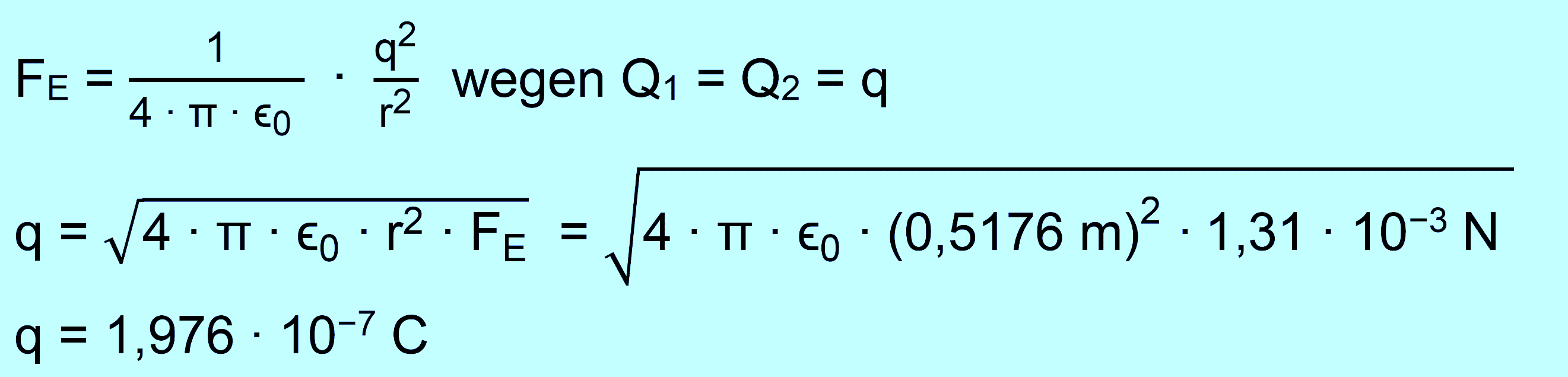|
Klausuraufgaben-Kräfte
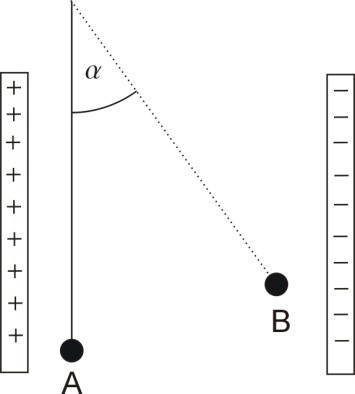
im Feld Teil 1 In dem homogenen Feld eines Plattenkondensators hängt
eine kleine Alukugel an einem Isolierfaden. Der Faden ist an der Decke
befestigt. Die Kondensatorplatten liegen in der Vertikalen (s.
Abb.) und haben einen Abstand von 30 cm. Es wird eine Spannung von 3000
V am Kondensator anlegt.
a.) Die Alukugel weist eine
Masse von 0,5 g auf. Welche Anfangs- beschleunigung erfährt die Kugel im Feld des Kondensators, wenn sie eine Ladung von q = + 5 ∙ 10−8
C erhält. b.) Bestimmen Sie den Winkel α zur
Anfangslage, der vorliegt, wenn die Kugel in B zur Ruhe kommt? Erläutern Sie Ihren Ansatz
ausführlich, indem Sie die angreifenden Kräfte
im Punkt B eintragen. Teil 2 [Hinweis: möglichst exakt rechnen] Anstelle des Plattenkondensators wird jetzt eine
positiv geladene Kugel K an die Stelle A des Probekörpers geschoben, so
dass der Probekörper eine Auslenkung α von 10° erfährt. Die
Länge des Iso- lierfadens beträgt 1 m. a.) Berechnen Sie die Entfernung r zwischen den
Mittelpunkten der Kugeln [Zur Kontrolle: r =17,43 cm]. b.) Untersuchen Sie, wie groß ist die elektrische
Feldkraft auf den Probekörper ist? Skizzieren Sie hierzu
die angreifenden Kräfte im Punkt B. Teil 3 Der Plattenkondensator wird wie in Teil 2 entfernt. Man hängt an den gleichen Aufhängepunkt wie bei der ersten Alukugel
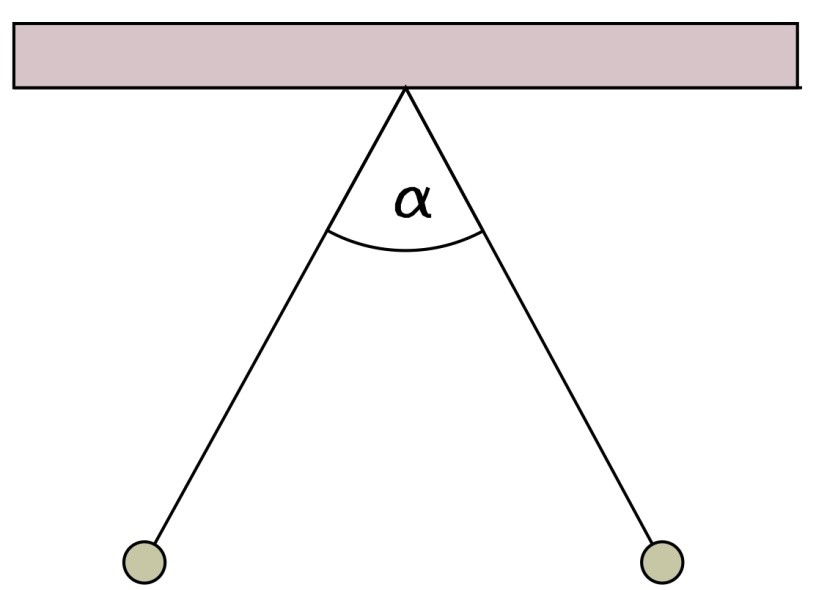
eine zweite völlig gleiche Alukugel mit gleicher Fadenlänge ( 1m ). Es hängen jetzt also zwei völlig identische Alukugel am gleichen
Aufhängepunkt neben- einander. Auf beide Kugeln wird jeweils die gleiche Ladung q übertragen. Die Kugeln
stoßen sich dann ab und kommen bei einem Ablenkwinkel α von 30°
zur Ruhe. Bestimmen Sie die Entfernung der Kugelmittelpunkte und
die Größe der elektrischen Feldkraft auf eine Kugel. Skizzieren
Sie auch hier die angreifenden Kräfte an einer Kugel.
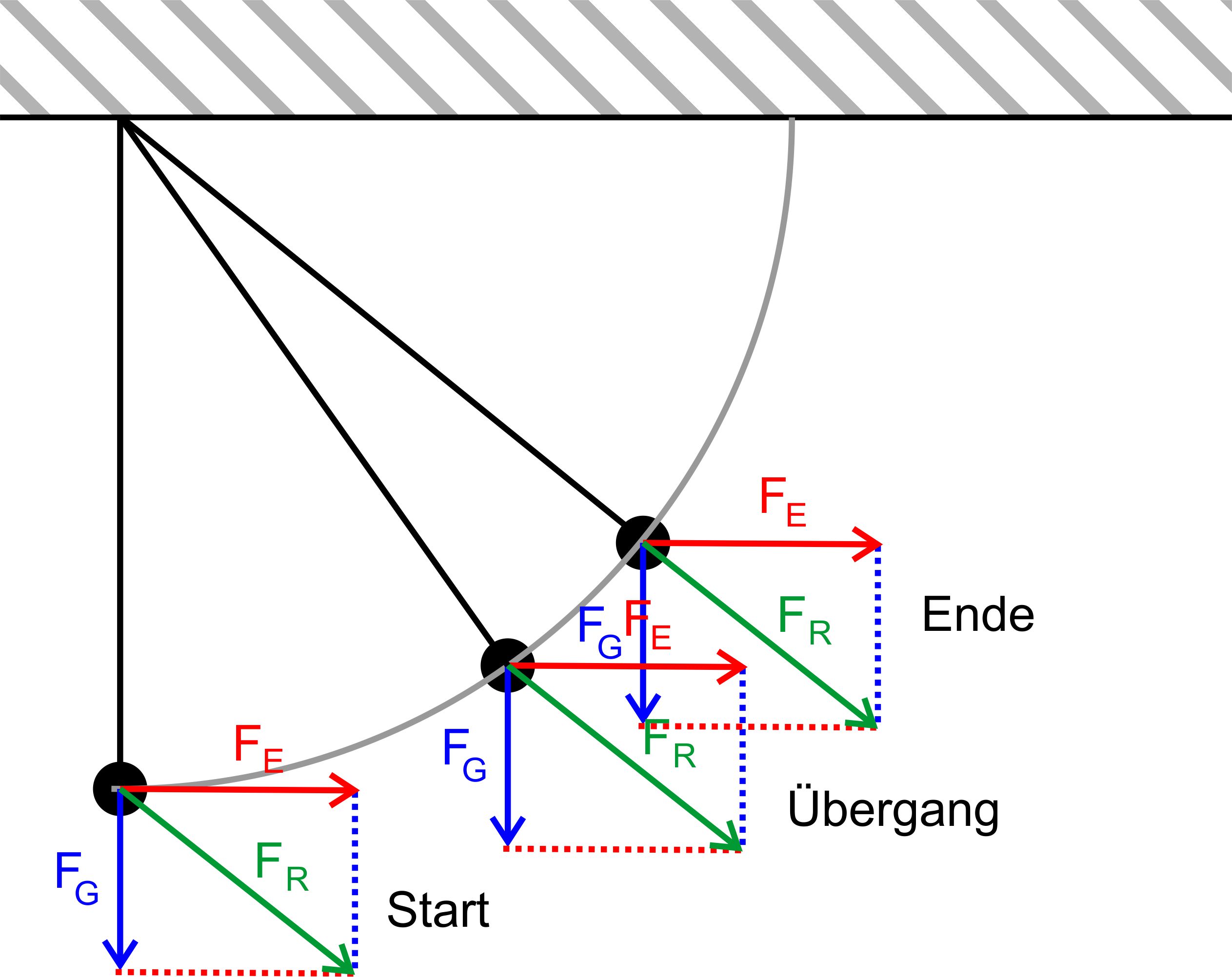
allgemeine Überlegungen Wir wollen zunächst einmal ein paar allgemeine Überlegungen zu den Kräften am Fadenpendel im Kondensator machen, um zu er- kennen, welche Kraft für die Beschleunigung in den jeweiligen Win- kellagen zuständig ist. Hierzu zunächst folgende Zeichnung
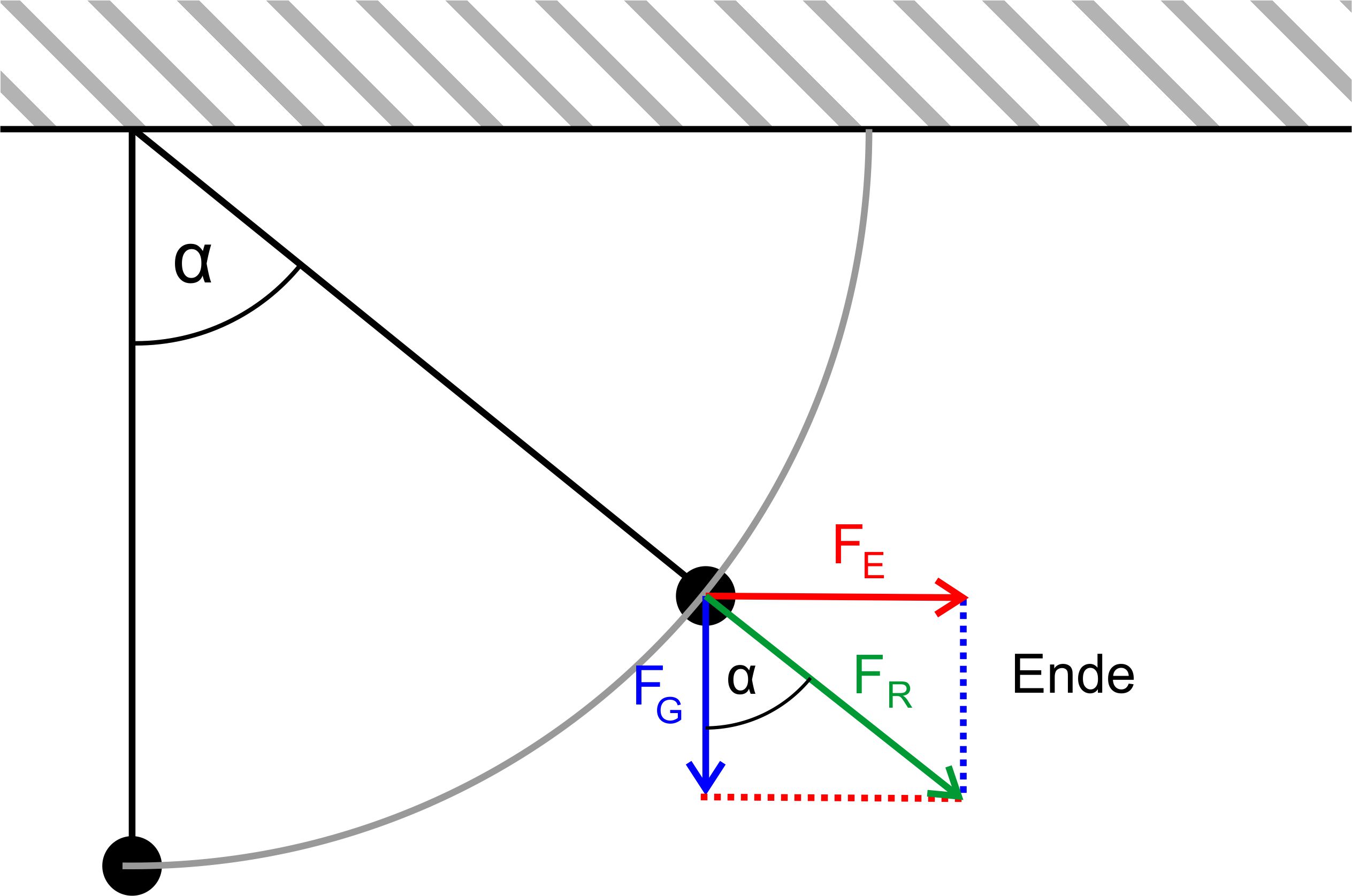
Es herrschen im Kondensator zwei Kräfte,
einmal die Gewichtskraft FG = m ∙ g und die elektrische
Feldkraft FE = q ∙ U/d. Die
resultierende Kraft FR ergibt sich durch Vektoraddition. Die Gewichtskraft zeigt immer zum Erdmittelpunkt, also in der Ab- bildung nach unten. Sie ist konstant, da sich m nicht ändert. Die elektrische Feldkraft zeigt entlang der Feldlinien, also immer senkrecht zu den Platten. Sie ist ebenfalls konstant, da ein homogenes Feld vorliegt. Es ergibt sich somit in jeder Winkelposition dasselbe Kräfte- paar. Warum bewegt sich jetzt die Alukugel überhaupt? Hierzu muss man sich die resultierende Kraft ansehen. Hierzu ebenfalls eine Abbildung.
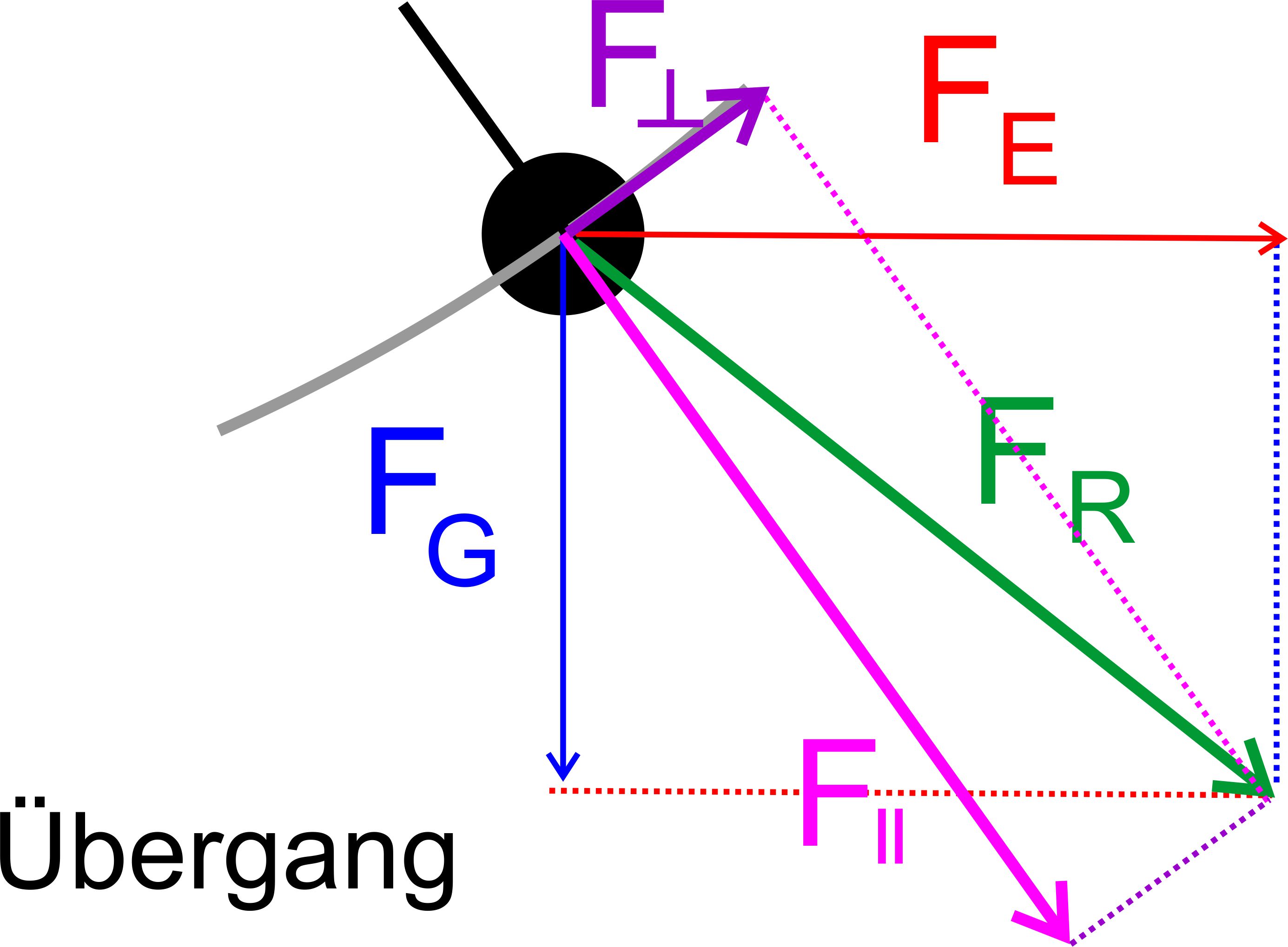
Wir befinden uns in einer mittleren Winkelstellung. Die
resultierende Kraft FR lässt sich zerlegen in eine Komponente FꞱ tangential zum Kreisbogen, also senkrecht zum Faden, und eine Komponente entlang des Fadens F║. F║ zieht entlang des Fadens, hält ihn also straff gespannt, während FꞱ für die Bewegung entlang des Kreisbogens sorgt. Solange es die Komponente FꞱ gibt, wird eine Bewegung
stattfinden. Am
Start entspricht FꞱ der elektrischen Feldkraft FE. Mit größerem Winkel
α wird FꞱ immer kleiner. Sobald FR entlang des
Fadens zieht, also F║
entspricht, hört die Bewegung
auf, weil die Komponente FꞱ nicht
mehr vorliegt. Teil
1: Am Start sorgt FE
für die Bewegung, also die Beschleunigung a. Mit Hilfe der Grundgleichung
der Mechanik wird a bestimmt.
Zunächst die Abbildung zu den Kräfteverhältnissen (s. auch oben):
Aus der Abbildung
entnimmt man
Teil
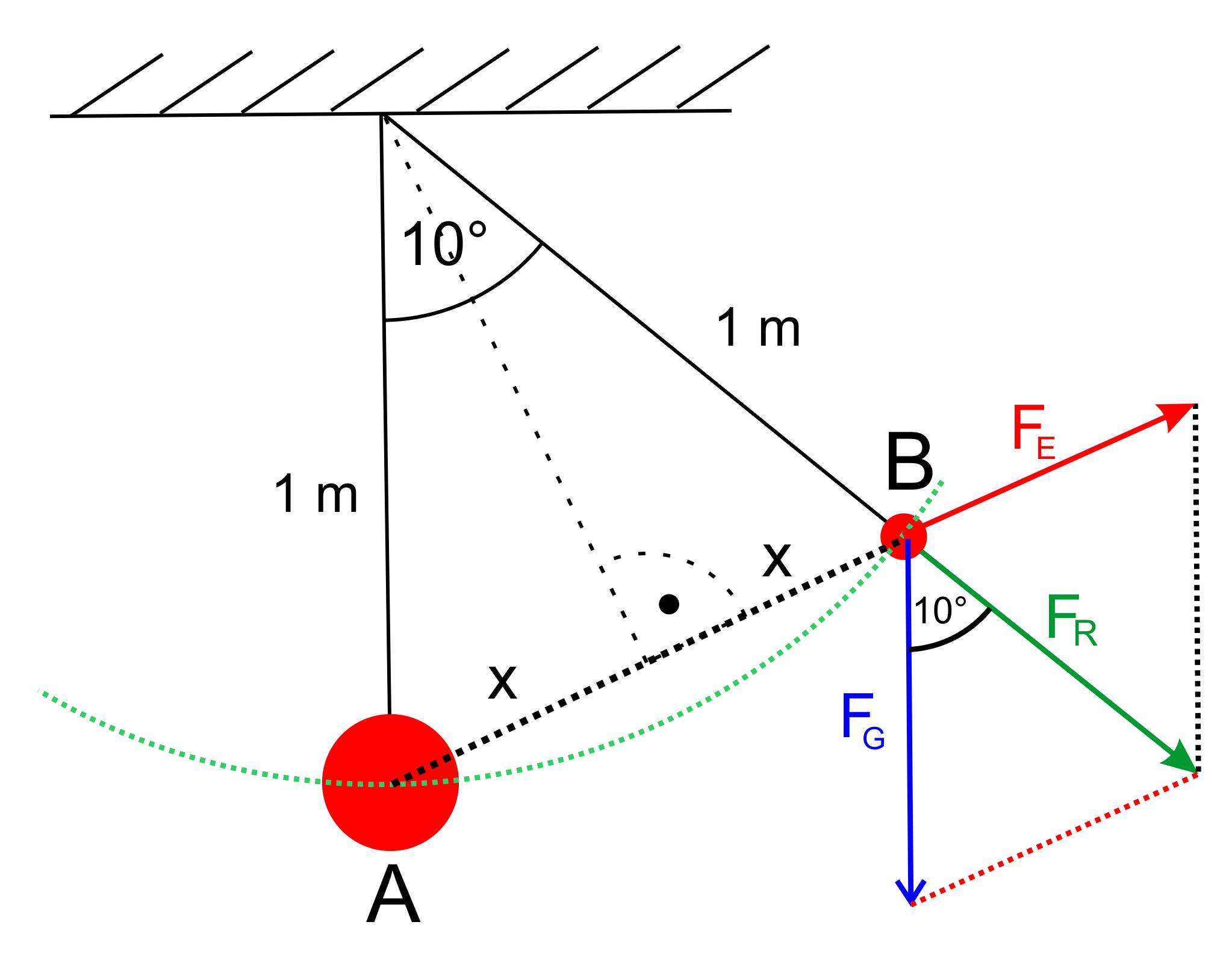
2: hier
zunächst die Skizze der Kräfte
Bei der
Richtung von FG und FR ändert sich nichts. FE
zeigt allerdings radial
weg von der Kugel bei A. Es liegt ja ein radialsymmetrisches
Im
Gegensatz zur
Abbildung im Kapitel „Feldstärke Existenz“ kann man
hier jetzt Berechnungen anstellen, da ein
gleichschenkliges Drei- eck vorliegt. Berechnung des
Abstandes r:
Berechnung von FE
auf verschiedene Weisen möglich 1. Fall: Strahlensatz Da die Winkel im „oberen
Dreieck mit den Fadenlängen“ und im „unteren Dreieck mit
den Kräften“ gleich groß sind, kann man die Dreiecke
ineinanderlegen. Beide Dreiecke sind übrigens wegen der Lage von FE
gleichschenklig, d.h. FG muss FR
entsprechen. Man erhält dann eine
Strahlensatzfigur. Es gilt also:
2. Fall: über Winkel
(ähnlich wie bei „x“)
Exkurs: Falls man schon das Coulombsche Gesetz kennen würde, könnte man jetzt auch die Ladung der Kugel bestimmen.
Teil
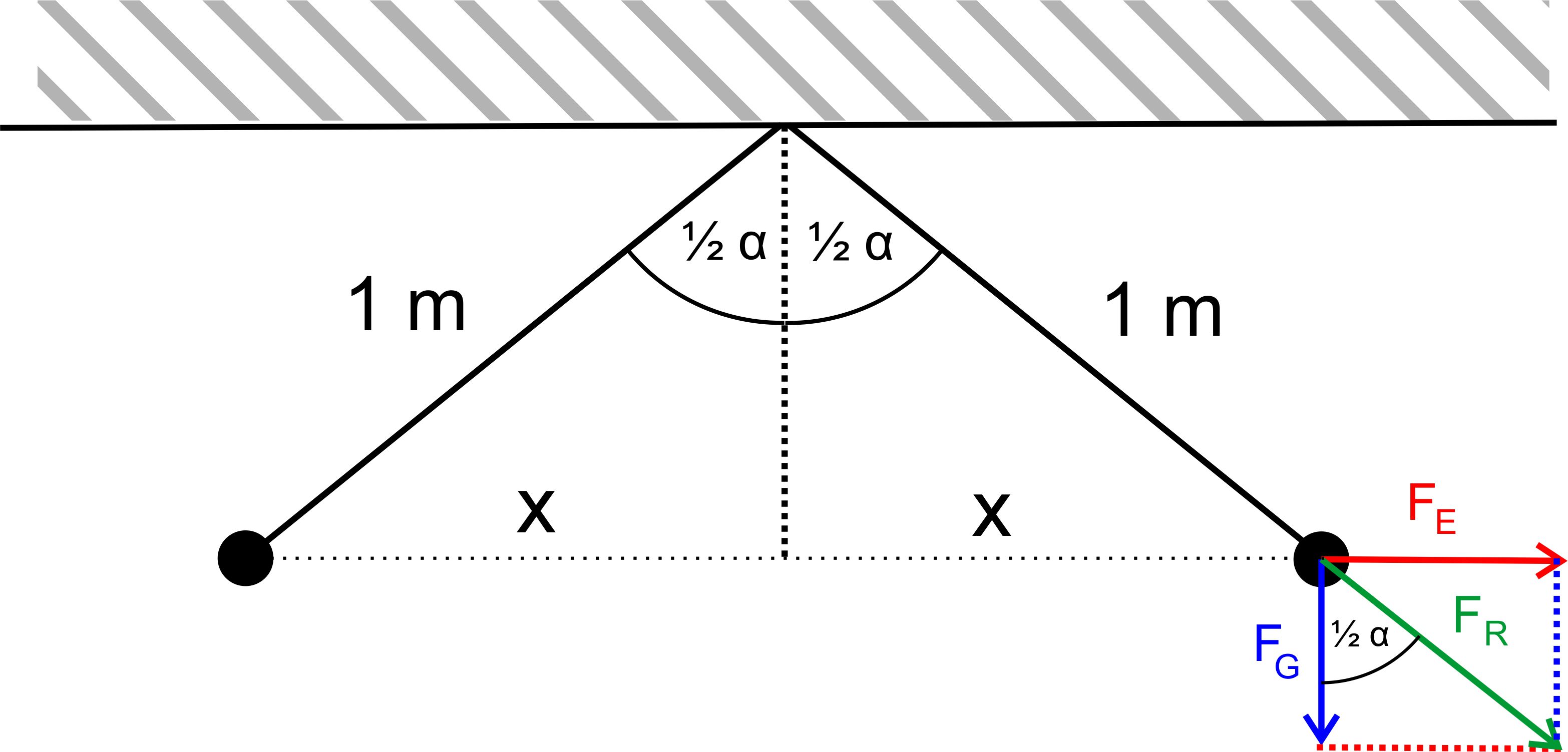
3: hier zunächst
die Skizze der Kräfte
Kräfteverhältnisse
ähnlich wie bei Teil 1. Rechnung ähnelt Teil 1 + 2. Berechnung
vom d = Abstand der Kugeln: gleichschenkliges
Dreieck liegt vor, also
Berechnung
der elektrischen Feldkraft wie Teil 1
Bei
Kenntnis von Coulomb berechnet sich q so:
- zu Teil 1 Aufgabe 1 - zu Teil
2 Aufgabe 1 - zu Teil 3 Aufgabe 1 - Lösung Teil 1 - Lösung
Teil 2 - Lösung Teil 3 - zum Kapitel „Plattenkondensator-Linkliste" |