|
Übungsaufgaben
- Fadenstrahlrohr Aufgabe
Nr.1 (leicht, mittel) In einem
Fadenstrahlrohr werden die Elektronen mit einer Spannung von 200 V
beschleunigt und in ein sekrecht stehendes
Magnetfeld der Stärke B =
3 mT eingeschossen. Wie groß
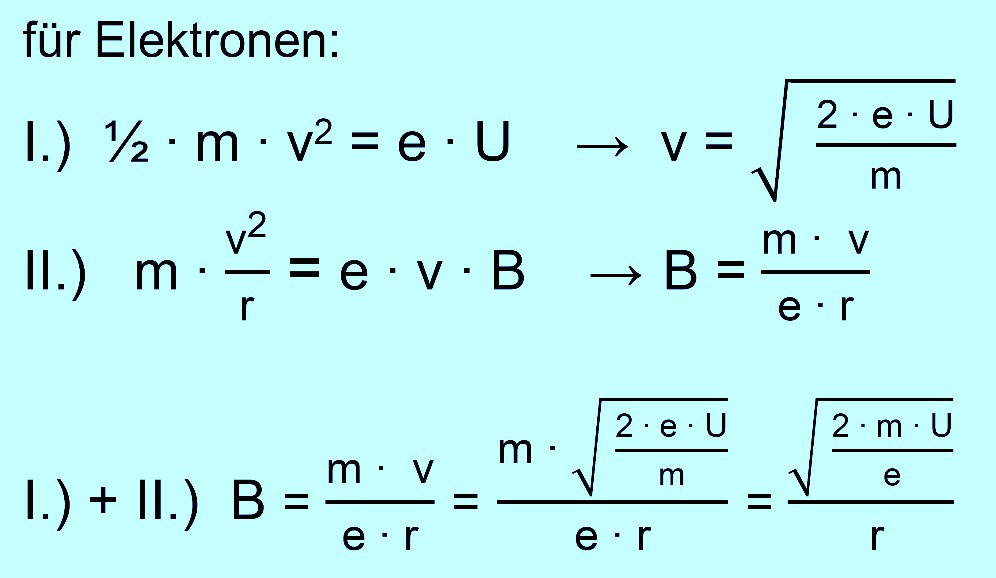
ist der Kreisradius? Welchen Wert hat die Umlaufdauer? Lösung: Man geht von den zwei grundlegenden Zusammenhängen aus, die schon im Kapitel „Fadenstrahlrohr-Messungen“ genannt wurden.
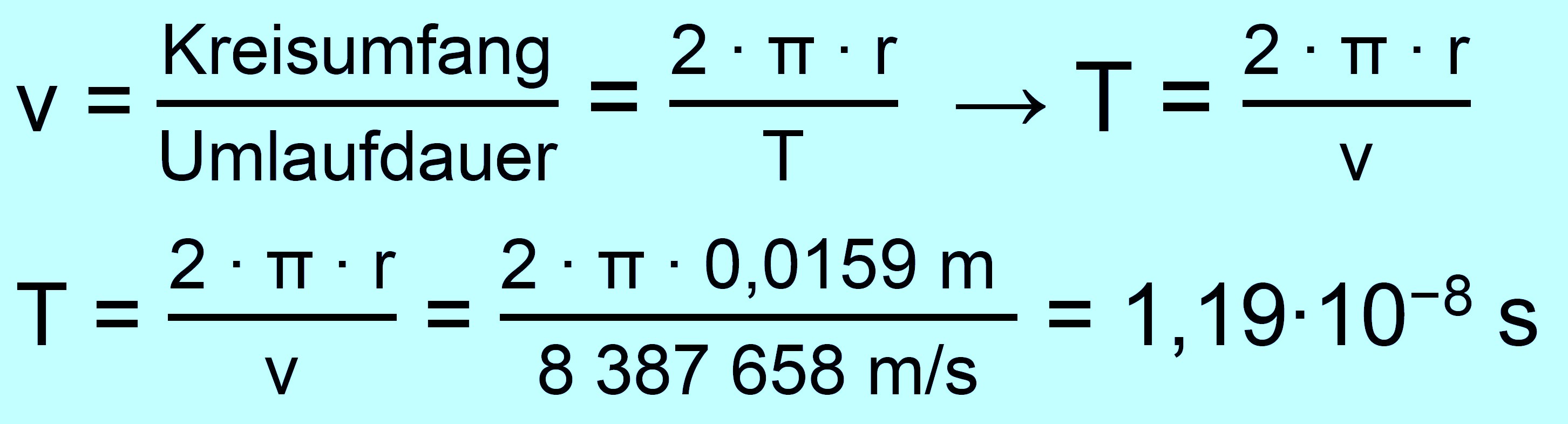
Für die Umlaufdauer kann man im Kapitel „Kreisbewegungen“ nachsehen und erhält ausgehend von der Formel für die Bahnge- schwindigkeit eine Formel für T.
Aufgabe
Nr.2 (leicht) In einem Fadenstrahlrohr hat die Kreisbahn einen Radius von r = 5 cm. Die
Umlaufdauer hat einen Wert von T = 2∙10−8 s. Berechne B,
v und U. Lösung: Vorgehen wie bei der Aufgabe Nr.1. Es wird nur anders umgestellt.
Aufgabe
Nr.3 (mittel, schwer) Bei einer
Beschleunigungsspannung U weisen Elektronen bei senkrechtem
Einschuss in ein Magnetfeld der Stärke B einen Radius von r = 4
cm auf. Man beschleunigt danach Alphateilchen (also He2+) mit dem
gleichen Spannungsbetrag und schießt diese in dasselbe Magnetfeld
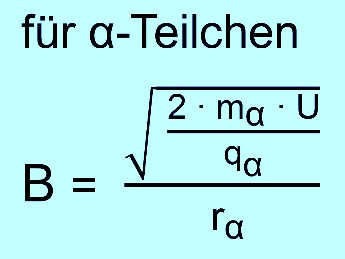
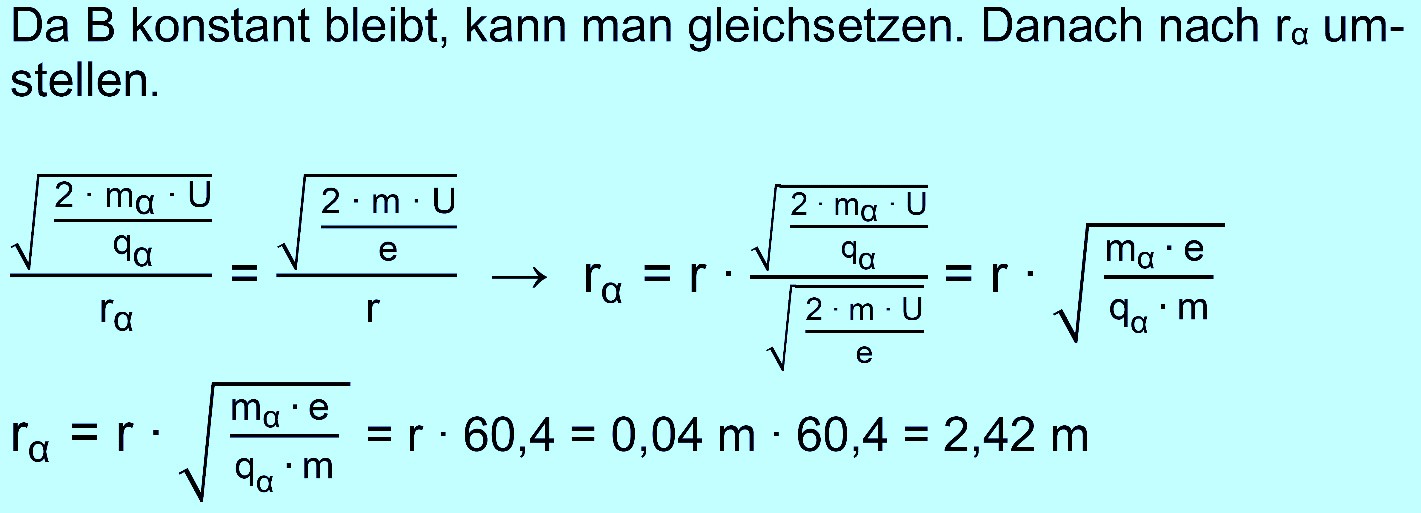
senkrecht ein. Wie groß ist jetzt deren Kreisbahn? Lösung: Vorgehen wie bisher. Wir nehmen die beiden üblichen Gleichungen. In die Formel für B setzt man jetzt die Formel für v ein.
Für die α-Teilchen muss man jetzt deren Masse mα und Ladung qα be-nutzen. Man erhält dann:
Es gilt: qα = 2 e und mα ≈ 7294 m. Daher wird rα wegen der größeren Trägheit deutlich größer als re = r sein.
Aufgabe
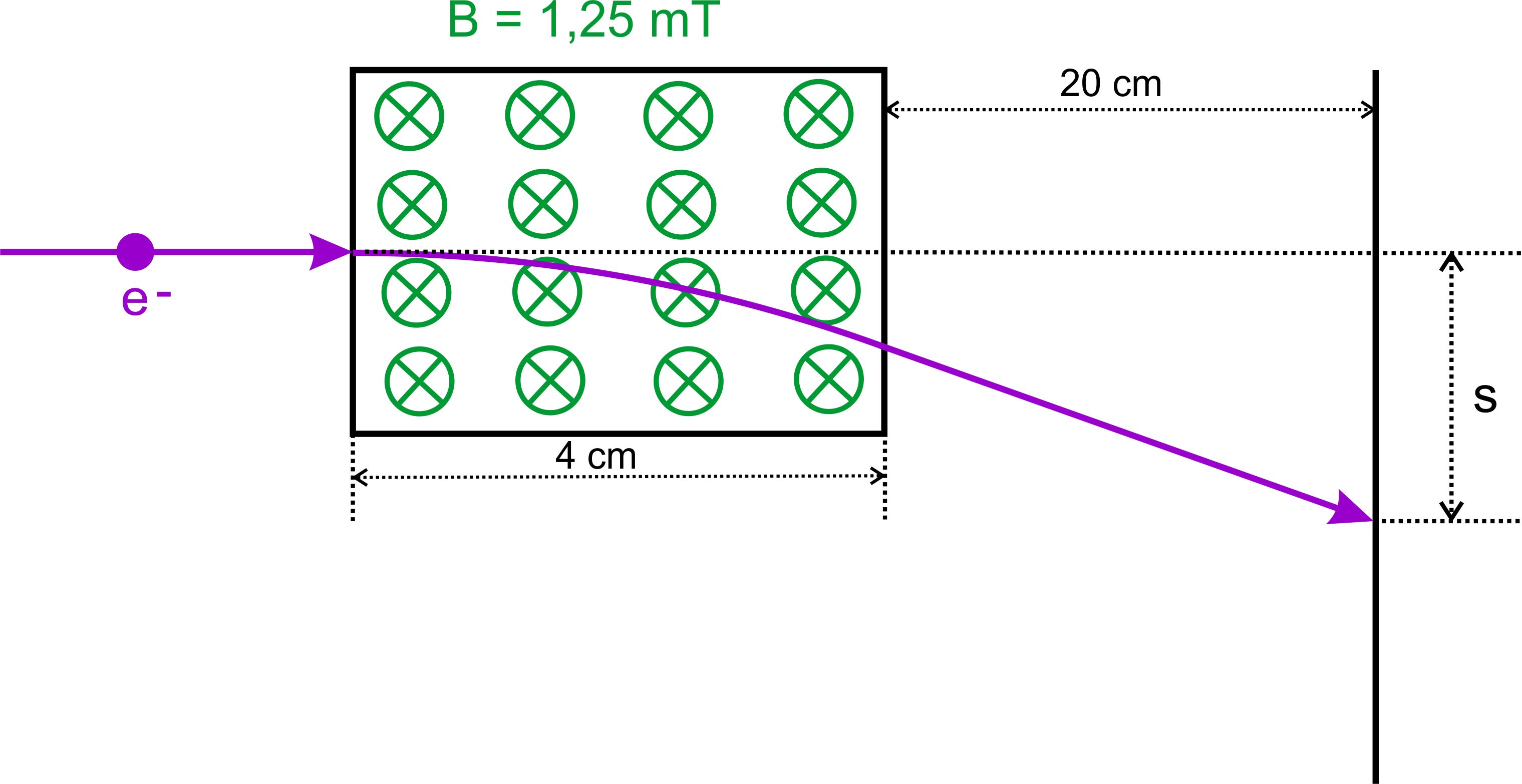
Nr.4 (schwer) Man schießt
Elektronen, die mit U = 3 kV beschleunigt wurden, senk-recht in Magnetfeld
der Stärke B = 1,25 mT ein. Das Magnetfeld hat eine
räumliche Ausdehnung von 4 cm. Auf einem Bildschirm, der in einem
Abstand von 20 cm vom Magnetfeld steht, treffen die Elektronen
auf. Um welche Strecke s sind diese Elektronen auf dem Bildschirm
von der Einschussrichtung abgelenkt worden? Die
folgende Abbildung zeigt noch einmal die Situation.
Lösung: Nach dem Austritt aus dem Beschleunigungskondensator bewegt sich das Elektron zunächst geradlinig, im B-feld auf einer Kreisbahn und danach wieder geradlinig. Wir bestimmen zunächst „v“ und „r“ auf die bekannte Weise (s. Nr.1).
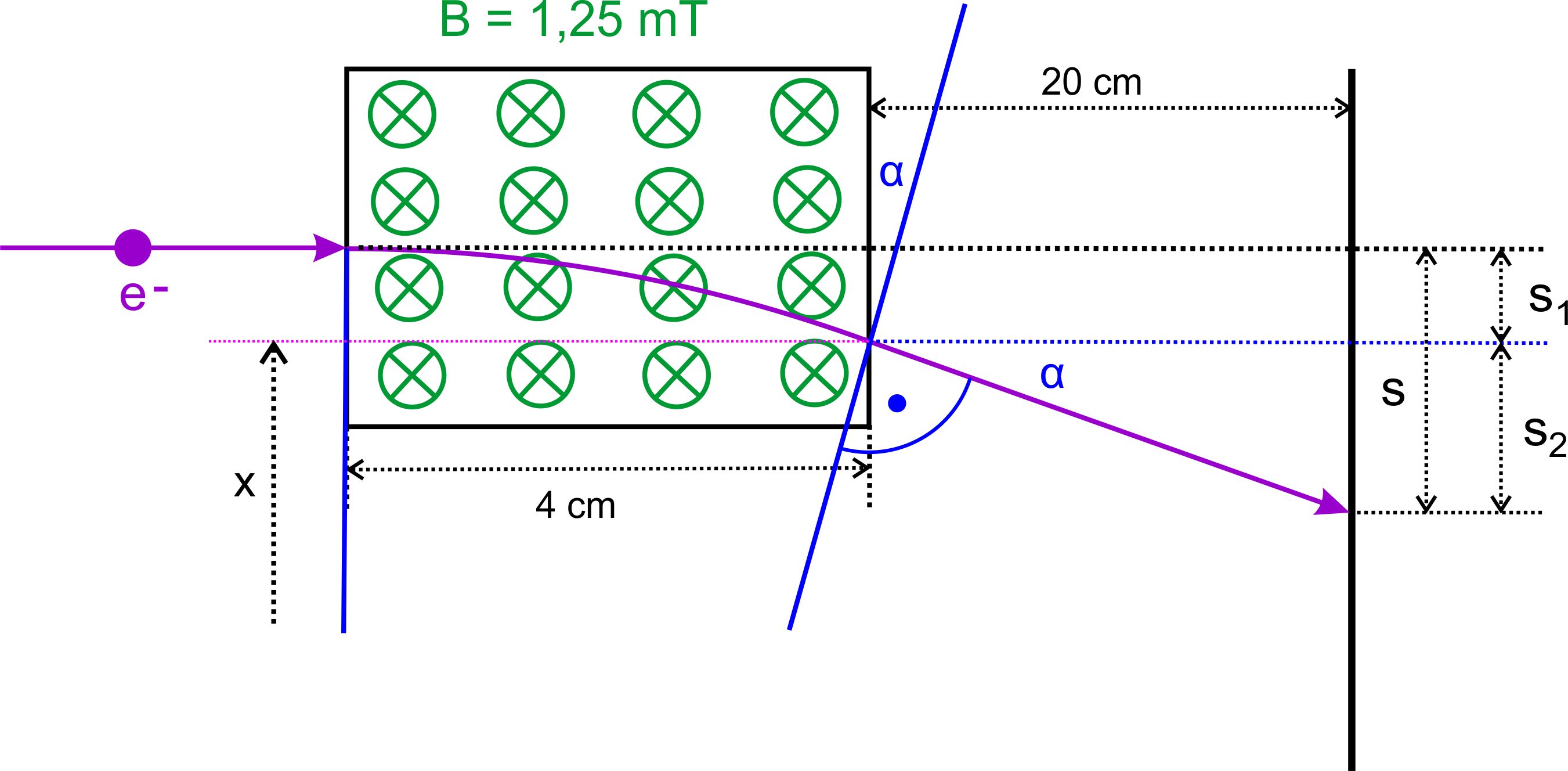
Als nächstes geht es vor allem darum, den Winkel α zu bestimmen, unter dem die Elektronen das Magnetfeld verlassen. Hierzu zu- nächst zwei Abbildungen. In die erste Abbildung ist der Winkel α des Kreisbogens eingetragen, den das Elektron im B-Feld beschreibt. In der zweiten Abbildung erkennt man, dass dieser Winkel dem Aus- trittswinkel entspricht (Stufenwinkel usw.)
Aus der ersten Abbildung gewinnen wir über das rechtwinklige Drei- eck zunächst α. s1 gewinnen wir über „x“ ebenfalls aus diesem Drei- eck. Der Winkel wird danach auch zur Bestimmung von s2 benutzt. Die Summe bildet dann das gesuchte „s“.
Dieser Aufbau entspricht der Ablenkeinheit bei den alten Röhrenbild-schirmen. Dort erzeugt eine Spuleneinheit Magnetfelder, die zur Ab- lenkung Elektronen dienen. Diese fahren dann zeilenweise über den Bildschirm und beleuchten diesen (s. Extra-Kapitel (in Arbeit)). Im Folgenden wird noch gezeigt, dass die Ablenkung bei festem U für kleine Ablenkwinkel α nur von B abhängt.
- zurück zum Kapitel „Messungen
mit dem Fadenstrahlrohr“ - zurück zum Kapitel „Fadenstrahlrohr
allgemein“ - zurück zum Kapitel „
allgemeine Formeln für die Lorentzkraft bewegte Ladung“ - zurück zur Übersicht „Felder“
|