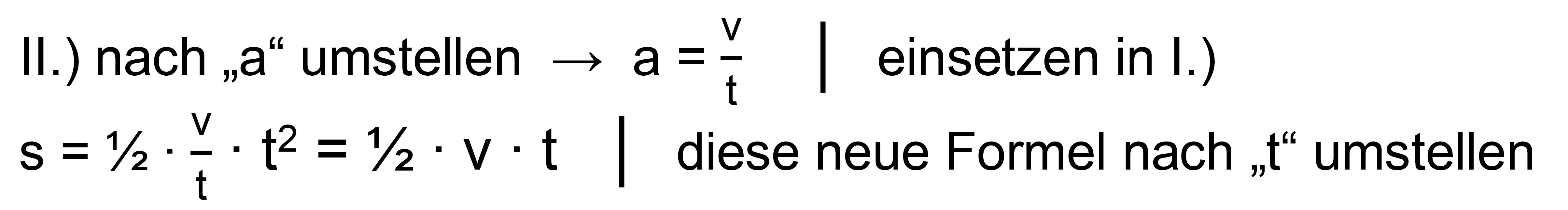|
zur
Aufgabe: Übungsaufgaben Übungsaufgabe Nr.1 Der Fall eines Wattebausches wird mit einer Videokamera aufgenom- men
und mittels eines Videoanalyseprogrammes ausgewertet. Es
ergeben sich dabei folgende Messwerte für die Geschwindigkeit:
a.)
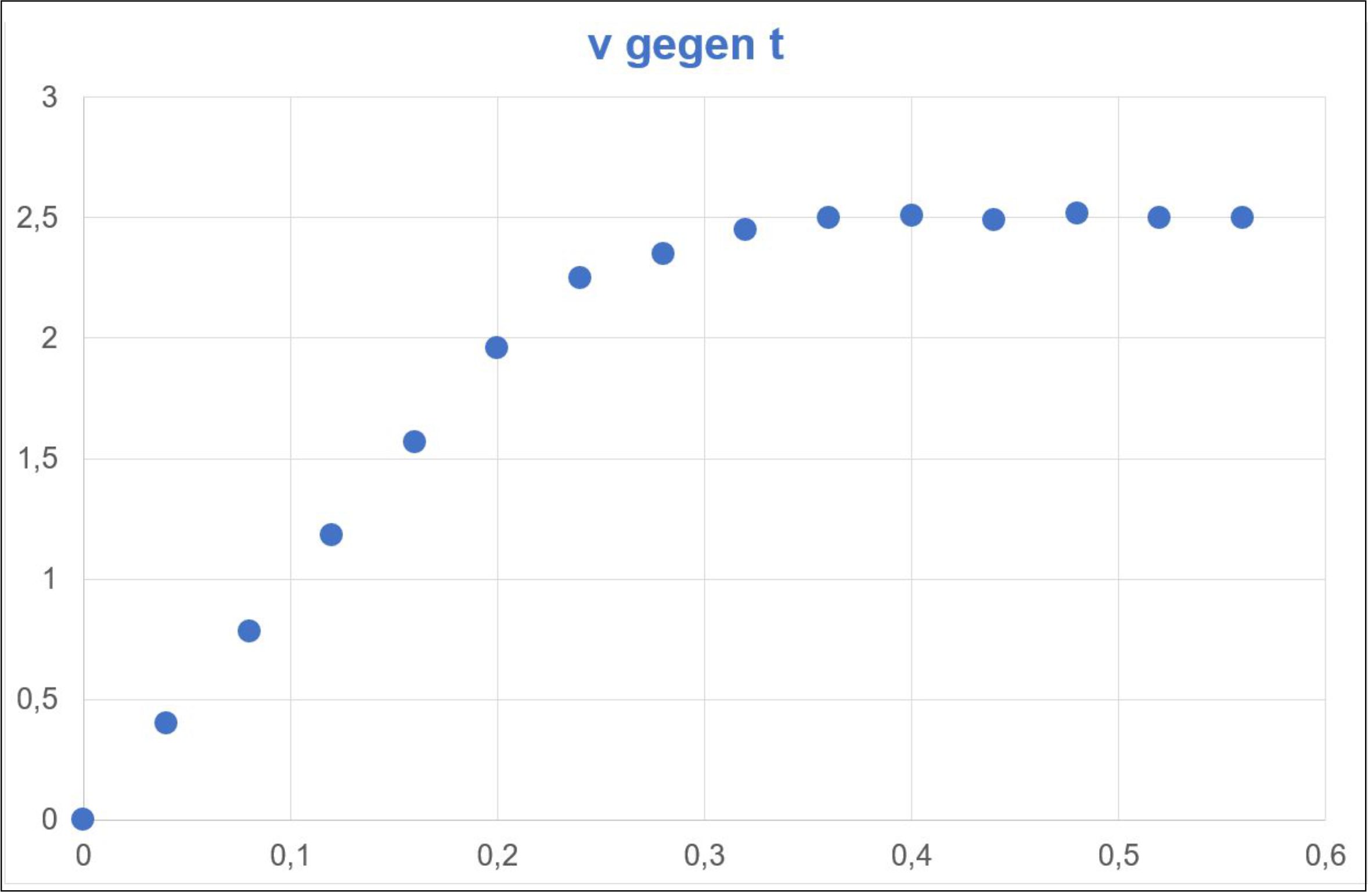
Fertigen Sie ein Zeit-Geschwindigkeits-Diagramm der gesamten Bewegung
an (auf
Millimeterpapier) (x-Achse = Zeit mit Einheit : 4 mm entspricht 0,04 s, y-Achse = Geschwindigkeits mit Einheit: 1 cm
entspricht 0,50 m/s) b.) Betrachten Sie jetzt den Bereich von 0 s bis 0,20 s und anschlie- ßend den Bereich ab 0,36 s
genauer. Welche Bewegungen liegen in den jeweiligen Zeitbereichen vor. Begründen Sie Ihre Aussagen. Geben Sie die Funktionsterme für die
jeweiligen Bereiche an. c.) Erklären Sie die Bewegung des Wattebausches über den gesamten Zeitraum. Lösung: zu a.) Diagramm:(hier Excel-Diagramm)
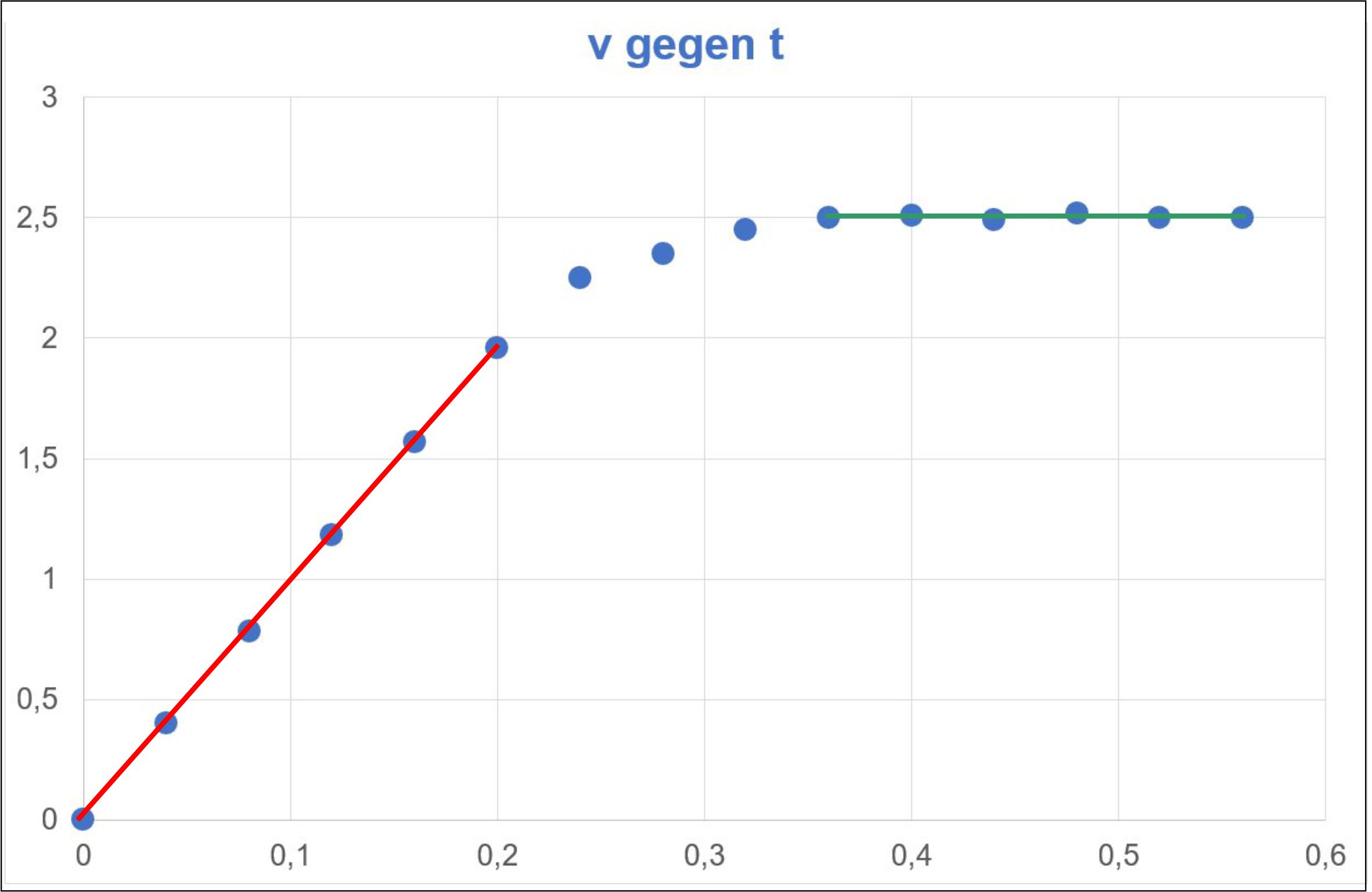
zu b.) Es werden wichtige Geraden in das Diagramm
eingetragen, so dass man folgendes Aussehen hat:
Zwischen 0 und 0,2 s hat
man eine gleichmäßige Zunahme der Ge- schwindigkeit, d.h. die Beschleunigung ist konstant. Es liegt hier eine gleichmäßig beschleunigte Bewegung vor. Es gilt v = a ∙ t. a erhält man als Steigung der Geraden. m = 1,96 m/s : 0,2 s = 9,8 m/s2 = a; es liegt ein freier Fall vor. Ab 0,36 s bleibt die Geschwindigkeit
konstant bei 2,5 m/s. Es liegt also eine gleichförmige
Bewegung vor mit der konstanten Geschwindigkeit v = 2,5 m/s. Funktionsterme: 0 bis 0,2 s v = 9,81 m/s2 ∙ t „freier Fall“ ab 0,36 s v = 2,5 m/s gleichförmig zu c.) Zunächst übt der Wattebausch einen freien Fall
aus, da er von der Gewichtskraft beschleunigt wird. Da er aber in
Luft fällt, liegt ein Luft- widerstand vor. Dieser nimmt mit
der Geschwindigkeit (quadratisch) zu und wirkt der Gewichtskraft immer stärker
entgegen ( 0,2 s bis 0,36 s). Ab 0,36 s ist die Luftwiderstandskraft genauso groß wie die Gewichts- kraft und der Wattebausch wird nicht mehr beschleunigt und fällt mit konstanter Geschwindigkeit. Extra: Mehr zum Luftwiderstand
in diesem Kapitel: Skispringen real
oder in diesem Lernvideo. Übungsaufgabe Nr.2 Ein PKW
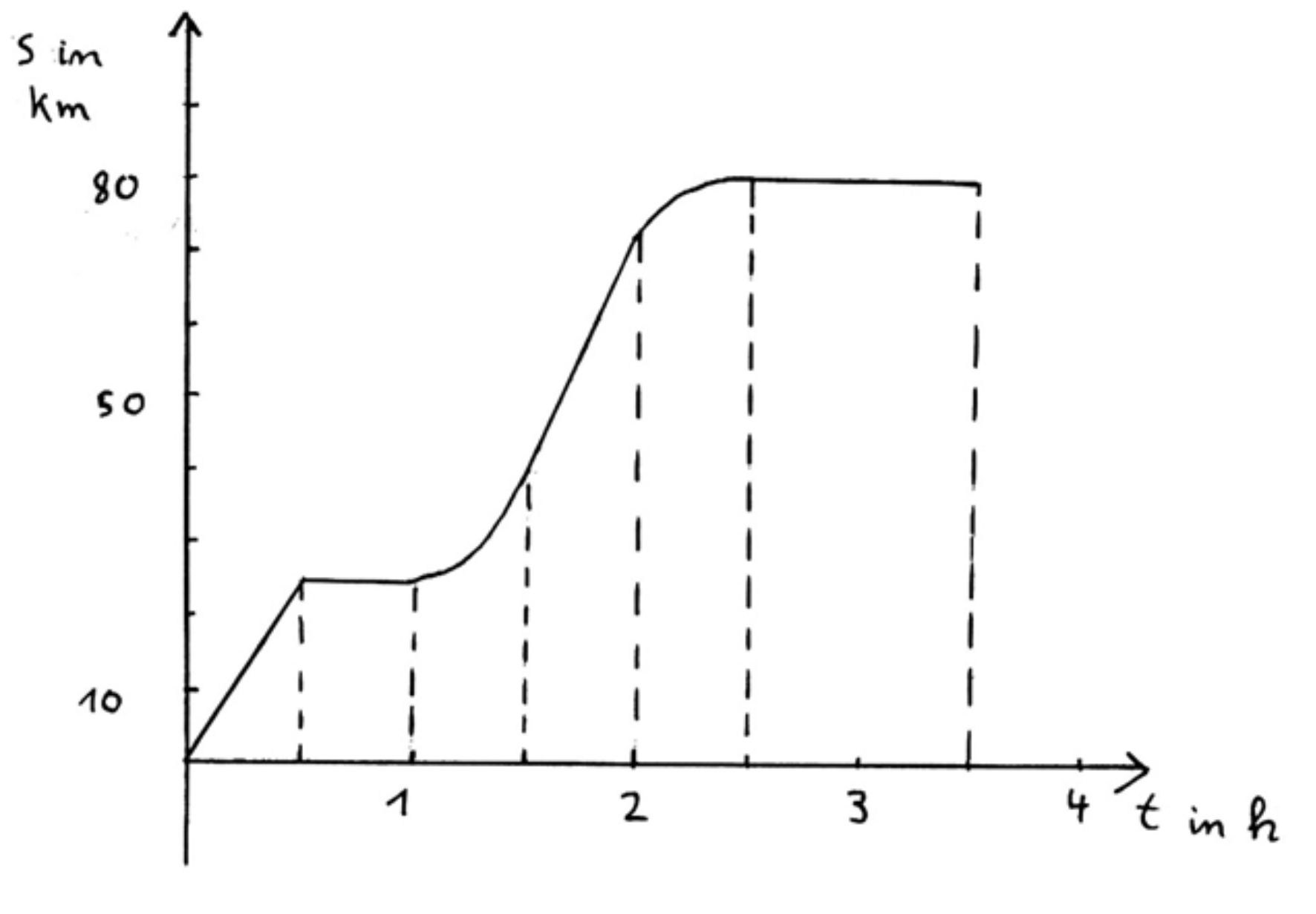
fährt zum Zeitpunkt t = 0 s an einem Ort A los. Das Zeit- Weg-Diagramm
dieses PKWs ist in der Abbildung zu sehen. Geben Sie an,
welche Bewegung der PKW in den einzelnen Abschnitten (gestrichelte Linien) durchführt. Begründen Sie Ihre Behauptungen anhand der
Abbildung! (s gibt die Wegstrecke an, die der PKW von A aus zurückgelegt hat) Lösung: −
0 h bis 0,5 h: Gleichförmige Bewegung, da s konstant mit t zunimmt, d.h. es gilt: s = k ∙ t, mit k = v =
25 km/0,5 h = 50 km/h. −
0,5 h bis 1 h: Stillstand ab 25 km, der PKW bewegt sich nicht, da s konstant bleibt −
1 h bis 1,5 h: Die Streckenlänge pro Zeiteinheit nimmt mit der Zeit zu, möglicherweise ein quadratischer
Zusammenhang → beschleunigte Bewegung, bei quadratischem Zusammenhang:
gleichmäßig beschleunigte Bewegung (s = ½ ∙ a ∙
t2). −
1,5 h bis 2 h: gleichförmige Bewegung, da geradliniger Verlauf (s. 0 h bis 0,5 h), v ≈ 30 km/ 0,5
h = 60 km/h − 2 h bis 2,5 h: Streckenlänge pro Zeiteinheit nimmt ab, der
PKW wird langsamer, er bremst ab; falls ein
quadratischer Zusammenhang besteht,liegt eine gleichmäßige Abbremsung
(negative Beschleu- nigung) vor −
ab 2,5 h: PKW steht, da keine Strecke zurückgelegt wird Übungsaufgabe Nr.3 In der folgenden Tabelle sind die Messwerte einer Bewegung ange- geben. Gemessen wurde der zurückgelegte Weg ( in cm ) und die dafür benötigte
Zeit ( in s )
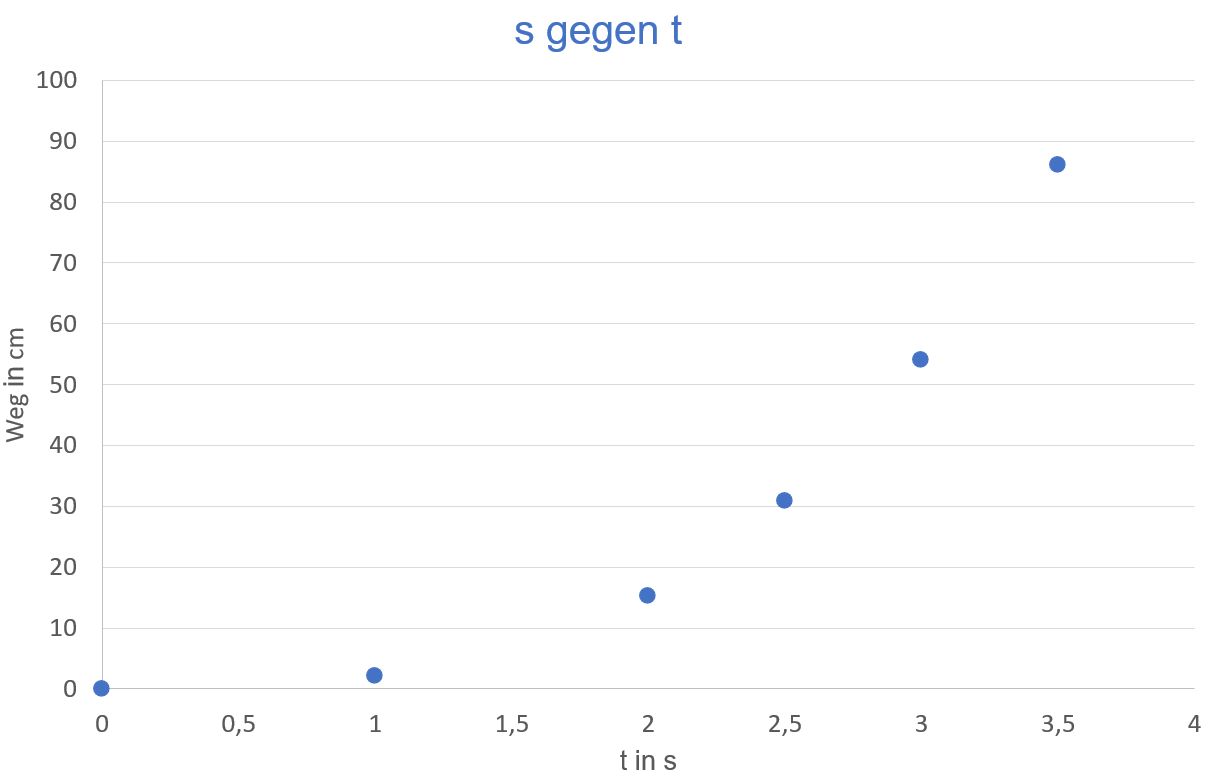
a.) Zeichen
Sie die Messwerte in ein Zeit−Weg−Diagramm. b.) Werten Sie
die Messwerte graphisch soweit aus, dass Sie eine Gleichung
erhalten, mit der Sie den Weg aus der Zeit bestimmen können. c.)
Handelt es sich um eine gleichförmige oder gleichmäßig beschleu- nigte
Bewegung? Begründen Sie Ihre Antwort. Lösung: zu
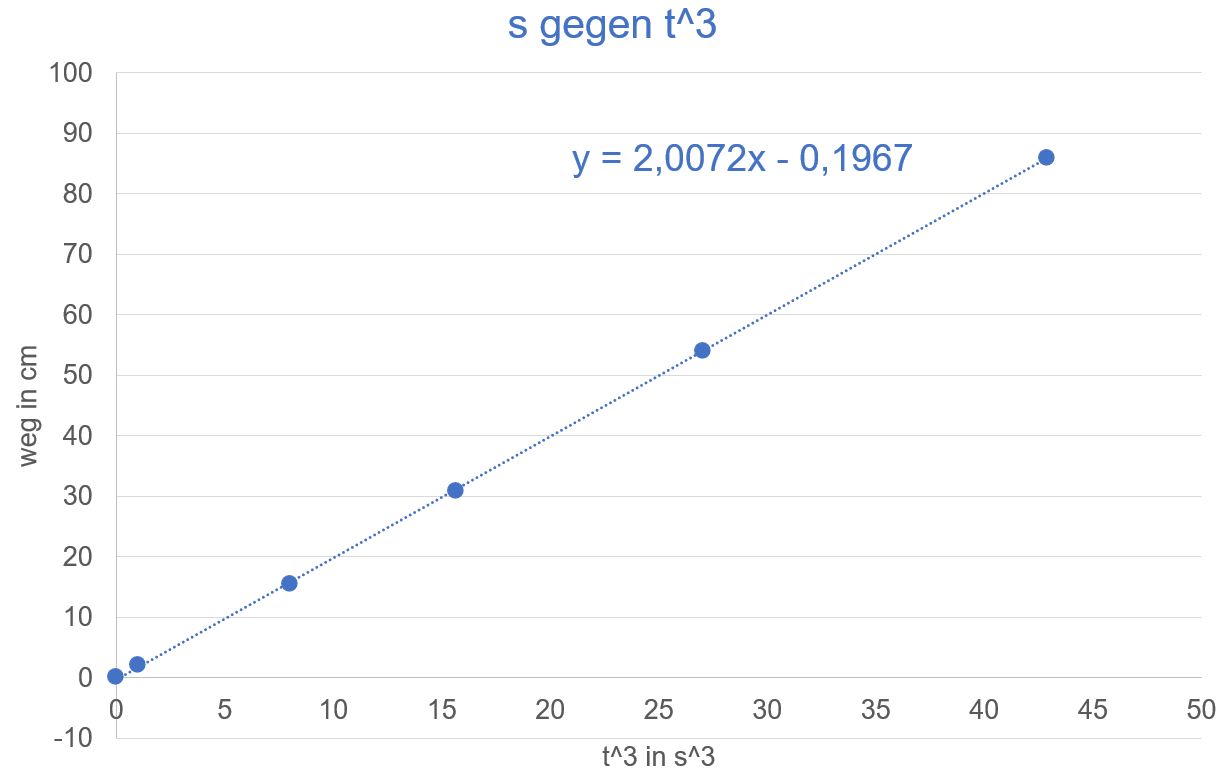
a.) 1. Schritt: s gegen t auftragen
Ergebnis: es ergibt sich keine Gerade → weiter auswerten: s gegen t2 auftragen → immer noch keine Gerade → s gegen t3 auftragen. zu b.) Hier ergibt sich eine Ursprungsgerade (s. Abb.)
Dies bedeutet, dass der Zusammenhang s = k ∙ t3 mit k = 2 m/s3 vor- liegt. zu c.) Es
liegt keine der beiden Bewegungen vor, da bei einer gleichförmigen Bewegung im t-s−Diagramm
eine Gerade und bei einer gleichmäßig beschleunigten
Bewegung im t2-s−Diagramm eine Gerade auf- treten müsste. Übungsaufgabe Nr.4 Auf
einem Flugzeugträger steht einem Kampfjet eine Strecke von 94
m für einen Start zur Verfügung. Die Endgeschwindigkeit (Abhebe- geschwindigkeit)
soll 260 km/h (≈72,22 m/s) betragen. Bestimmen
Sie die Beschleunigung und die Startzeit, wenn man von einer
gleichmäßig beschleunigten Bewegung ausgeht. Lösung: gegeben: s = 94 m; v = 260 km/h ≈ 72,22 m/s; gleichmäßig
beschleunigt gesucht: t; a Es gibt als Standardformel nur: I.) s = ½
∙ a ∙ t2 und II.) v = a ∙ t In beiden Formeln wird zur Berechnung „a“ benötigt. „a“ ist aber nicht angegeben. Man muss also eine neue Formel aufstellen, in der „a“ fehlt und nur die gegebenen Größen vorkommen. Hierzu kann man eine Formel nach „a“ auflösen und diese dann in die andere Formel ein- setzen.
Videos
und Links zum Thema:
Man erkennt
bei den Videos sehr schön, dass der Start in Fahrtrichtung passiert. Somit
erhöht sich die relative Geschwindigkeit zwischen Flugzeug und Luft, so dass die Abhebegeschwindig- keit
reduziert werden kann. Übungsaufgabe Nr.5 Ein Güterzug hat eine Länge von 740 m mit 35 Waggons.
Er ersetzt damit
52 LKWs. Dieser Zug fährt zunächst mit 21,6 km/h durch einen Bahnhof.
Am Ende des Bahnhofs (t = 0 s) beschleunigt er gleichmäßig auf
90 km/h. Die Beschleunigung beträgt a = 0,3 m/s2. Wie
lange braucht der Zug für den Beschleunigungsvorgang von 21,6
km/h auf 90 km/h? Wie lang ist die Beschleunigungsstrecke? Lösung: gegeben: v0 = 21,6 km/h = 6 m/s; v = 90
km/h = 25 m/s; a = 0,3 m/s2 gesucht: t; s Im Weiteren gelten
die Formeln: (t und s wird ab dem Bahnhofsende
berechnet) s(t) = ½ ∙ a ∙ t2 + v0 ∙ t + s0 (mit s0 = 0 m) und
v(t) = a ∙ t + v0
Möglich wäre auch (s. Beispielaufgabe Nr. 4)
Link zum Thema: https://www.allianz-pro-schiene.de/themen/aktuell/740-meter-gueterzug/ Übungsaufgabe Nr.6 (sehr schwer) In der folgenden Tabelle sind die Messwerte einer Bewegung ange- geben. Gemessen wurde der zurückgelegte Weg (in m) und die dafür benötigte
Zeit (in s)
a.) Zeichen
Sie die Messwerte in ein Zeit−Weg−Diagramm. b.) Weisen
Sie graphisch nach, dass eine gleichmäßig beschleunigte Bewegung vorliegt. Hilfe: Lassen Sie eine polynomische Trendlinie (2.Grades) mittels einer Tabellenkalkulation (Excel) zeichnen. Sehen Sie sich die
Formel für die Trendlinie an. c.) Geben
Sie die Bewegungsgleichung an. Lösung: a.) Ein Excel-Diagramm
könnte folgendes Aussehen haben. Die Trendlinie ist
mit Formel eingetragen.
b.)+ c.) Da „x” für „t” steht, gilt also s(t) = 4 ∙ t2
+ 6 ∙ t + 50. Dies ent- spricht der Form s(t) = ½ ∙ a ∙
t2 + v0 ∙ t + s0, also der
Gleichung einer gleichmäßig
beschleunigten Bewegung mit a = 8 m/s2 , v0 = 6
m/s und s0 = 50 m. Die Bewegungsgleichung lautet somit s(t) = ½ ∙ 8 m/s2 ∙ t2
+ 6 m/s ∙ t + 50 m zurück
zu Aufgabe: zum vorherigen Kapitel zum nächsten Kapitel zurück zur |